第五单元圆同步练习(含解析)人教版数学六年级上册
文档属性
| 名称 | 第五单元圆同步练习(含解析)人教版数学六年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 296.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-22 17:43:07 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第五单元圆
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.圆的面积与它的( )无关.
A.圆心 B.半径 C.周长
2.从圆心到圆上任意一点的线段叫做( )
A.直径 B.半径 C.直线
3.如图,盒子内刚好放下5瓶罐头,每瓶罐头瓶底的半径为3 cm,盒子的长为( )cm.
A.15 B.25 C.30 D.20
4.一座台钟,钟面上分针的长度是1dm,这根分针走60分钟,针尖走过的路程是( )dm。
A.3.14 B.6.28 C.37.68 D.12.56
5.一个圆的半径由3cm增加到8cm,则它的面积增加了( )cm2。
A.55 B.39 C.55π D.39π
6.圆形花坛的半径是3m,在花坛外侧铺一条1m宽的小路,小路的面积是( )m2。
A.21.98 B.50.24 C.15.7 D.3.14
7.环形的内圆半径为6厘米,外圆半径为8厘米,求环形面积的算式是( )。
A.3.14×62+3.14×82 B.3.14×(8-6)2 C.3.14×(82-62)
8.在一个正方形里画一个最大的圆,圆的面积是正方形面积的( )
A. B. C. D.π
9.在古代,我国数学史上关于圆的研究记载着不一样的说法,下面( )种说法是描述圆心到圆上的距离一样长。
A.圆,一中同长也 B.圆出于方,方出于矩
C.圆,径一而周三 D.没有规矩,不成方圆
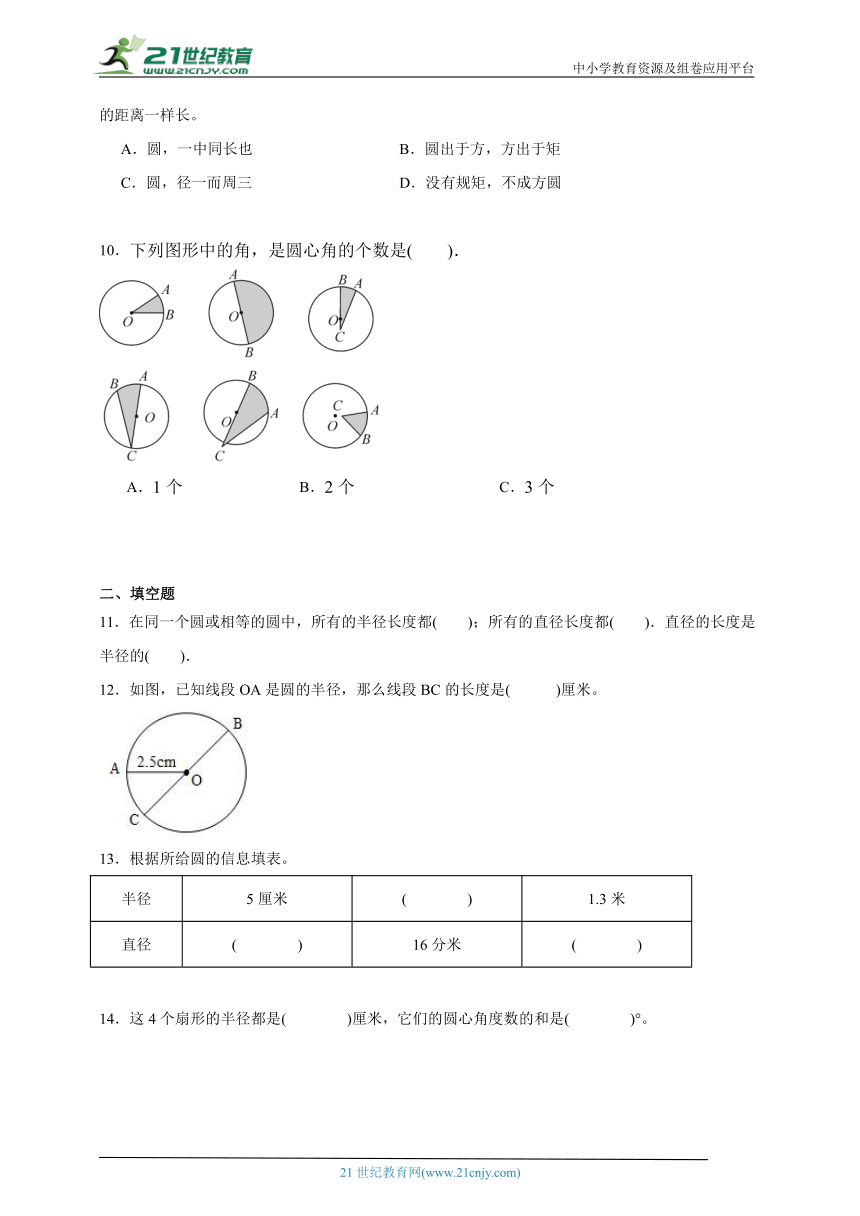
10.下列图形中的角,是圆心角的个数是( ).
A.1个 B.2个 C.3个
二、填空题
11.在同一个圆或相等的圆中,所有的半径长度都( );所有的直径长度都( ).直径的长度是半径的( ).
12.如图,已知线段OA是圆的半径,那么线段BC的长度是( )厘米。
13.根据所给圆的信息填表。
半径 5厘米 ( ) 1.3米
直径 ( ) 16分米 ( )
14.这4个扇形的半径都是( )厘米,它们的圆心角度数的和是( )°。
15.在边长是50厘米的正方形内画一个最大的圆,圆的直径是( )厘米。
16.如图,直角三角形的面积是12平方厘米,则阴影部分的面积是 .(结果保留π)
17.如图所示大半圆内有三个小半圆,大半圆弧长为28cm,那么阴影部分图形的周长是 .
18.判断正误。
(1)等式不一定是方程,方程一定是等式。( )
(2)在同一个圆中,圆心到圆上的距离处处相等。( )
(3)分母为8的最简分数共有4个。( )
(4)1千克的和3千克的相等。( )
(5)真分数都小于1,假分数都大于1。( )
19.用628cm长的铁丝围成一个正方形,这个正方形的面积是 cm2,如果围成一个圆,这个圆的面积是 cm2.从上面的计算数据中我们发现,当正方形和圆的周长相等时, 的面积更大.
20.图中AB=BC=CD=3厘米,则以AB为直径的圆的周长是以AC为直径的圆的周长的( ),以AB为直径的圆的面积是以AD为直径的圆的面积的( ).
三、判断题
21.两条半径和一条弧就组成一个扇形。( )
22.圆有无数条对称轴,半圆也有无数条对称轴。( )
23.如图,∠1是圆心角,∠2也是圆心角。( )
24.扇形比圆小. ( )
25.半圆的周长等于圆周长的一半。( )
四、计算题
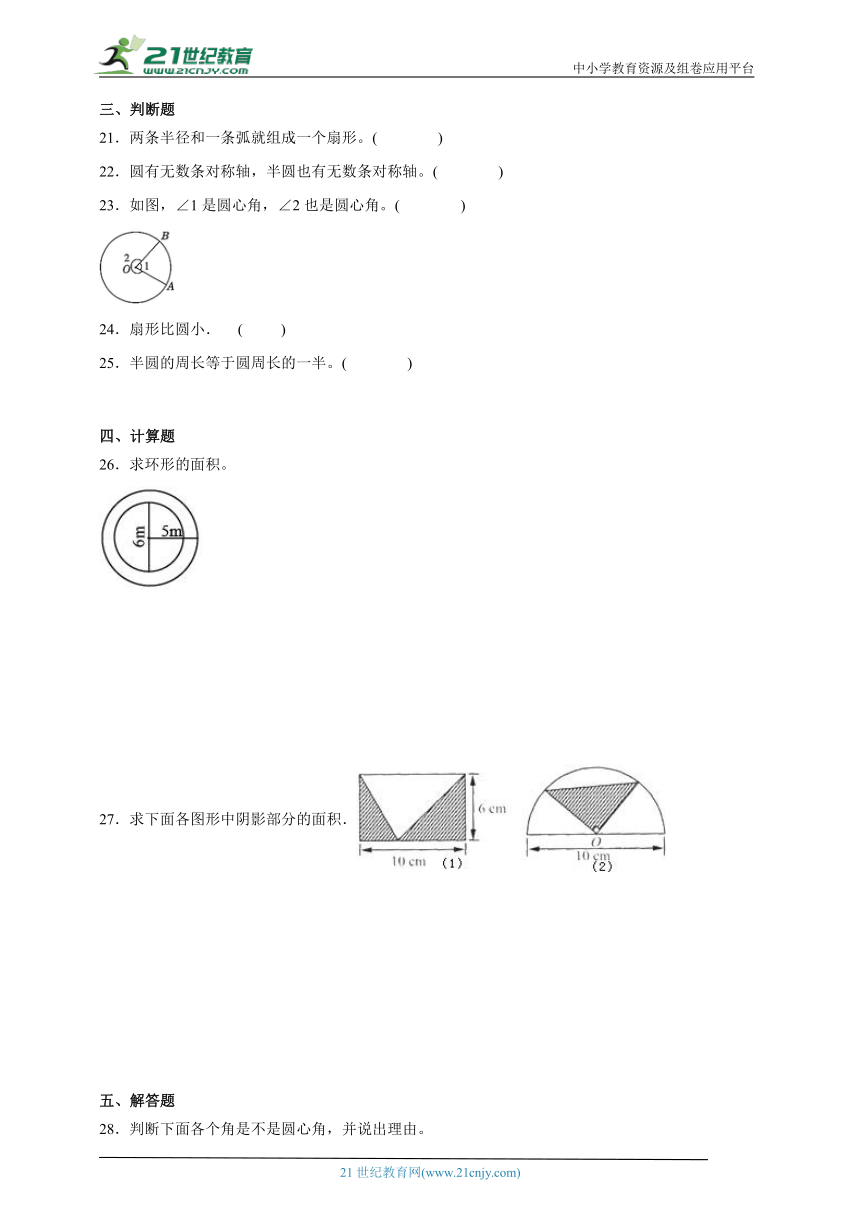
26.求环形的面积。
27.求下面各图形中阴影部分的面积.
五、解答题
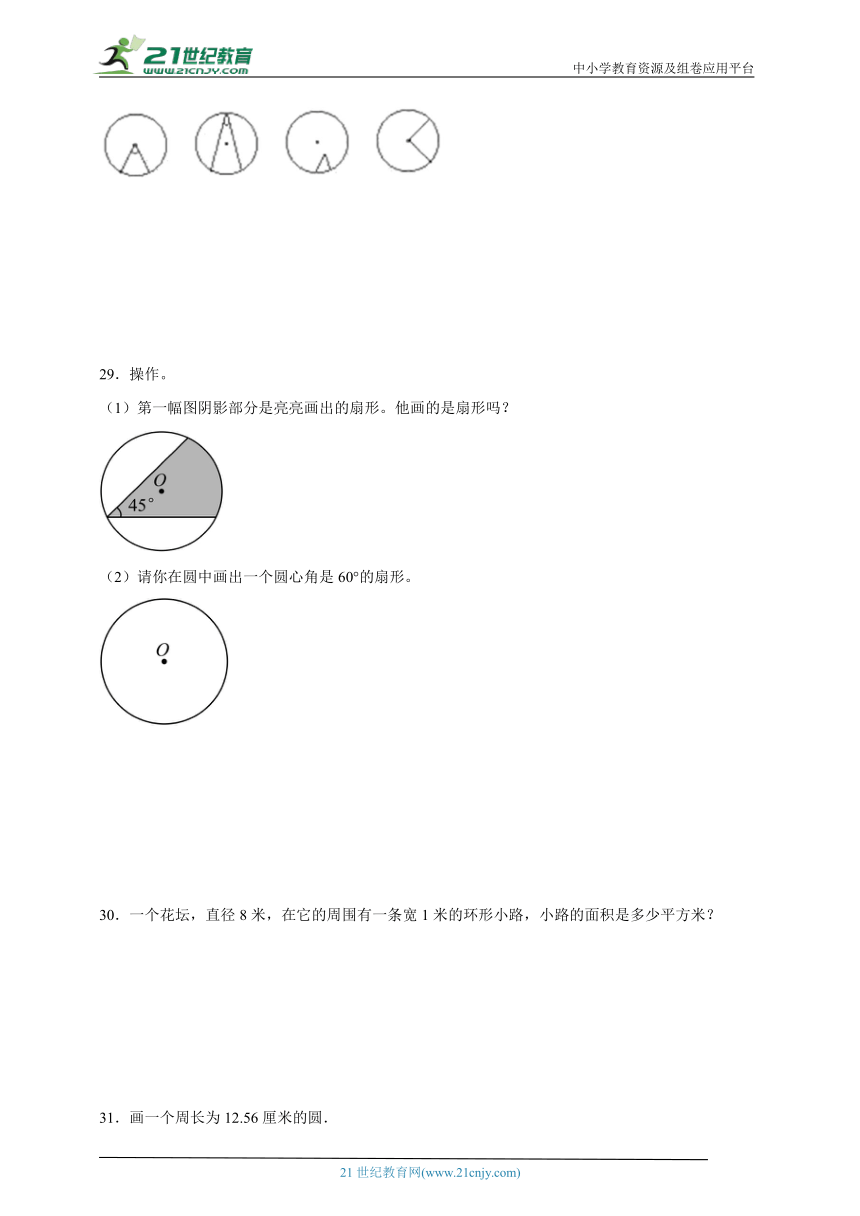
28.判断下面各个角是不是圆心角,并说出理由。
29.操作。
(1)第一幅图阴影部分是亮亮画出的扇形。他画的是扇形吗?
(2)请你在圆中画出一个圆心角是60°的扇形。
30.一个花坛,直径8米,在它的周围有一条宽1米的环形小路,小路的面积是多少平方米?
31.画一个周长为12.56厘米的圆.
要求:(1)先计算
(2)作图规范.
32.画一画,填一填.
(1)在如图的正方形中画一个面积最大的圆.
(2)如图是儿童乐园的平面图.
①小飞机在地图上的位置是( , )
②现在小李的位置是(5,4),他正在玩 .
《第五单元圆》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A B C B C A C C A B
1.A
【分析】根据圆的面积公式S=π ,圆的面积与圆的半径有关,又因为d=2r、C=2πr所以圆的面积与它的直径和周长也有关系,圆心只能确定圆的位置,而不能确定圆的大小.
【详解】圆的面积公式:S=π ,π是一个固定值,圆的面积大小与它的半径有关,与它的圆心无关.
2.B
【详解】根据半径的含义可知:从圆心到圆上任意一点的线段叫做半径.
故选B.
3.C
【详解】3×10=30(cm)
故答案为C
一共有5个圆,长方形的长就是一个圆半径的10倍,由此计算即可.
4.B
【分析】分针走60分钟就是走了一个圆,这个圆的半径就是分针的长度,则针尖走过的路程就是圆的周长,圆的周长=,代入数据计算得出周长。
【详解】(dm)
针尖走过的路程是6.28dm。
故答案为:B
5.C
【分析】圆的面积公式为S=πr2,代入公式先算出半径为3cm时小圆的面积,再计算出半径为8cm时大圆的面积,然后用大圆面积减去小圆面积即可。
【详解】π×82-π×32
=π×64-π×9
=64π-9π
=55π(平方厘米)
所以,它的面积增加了55π平方厘米。
故答案为:C
6.A
【分析】小路的形状是个圆环,花坛半径是小圆半径,花坛半径+小路宽=大圆半径,根据圆环面积=圆周率×(大圆半径的平方-小圆半径的平方),列式计算即可。
【详解】3+1=4(m)
3.14×(42-32)
=3.14×(16-9)
=3.14×7
=21.98(m2)
小路的面积是21.98m2。
故答案为:A
7.C
【分析】根据环形的面积=π×(R -r ),R表示外圆的半径,r表示内圆的半径,据此即可解答。
【详解】环形的面积=π×(R -r )代入数据可得:3.14×(8 -6 )
故选:C。
【点睛】此题考查的是环形的面积公式,属于常考题型,需熟练掌握。
8.C
【详解】试题分析:设正方形的边长为2,则正方形内最大的圆的直径就是2,由此利用正方形和圆的面积公式解答即可.
解:设正方形的边长为2,则正方形内最大的圆的直径就是2,
则正方形的面积是:2×2=4;
圆的面积是:π=π;
所以圆的面积是正方形的面积的:π÷4=.
故选C.
点评:抓住正方形内最大圆的特点,设出正方形的边长,从而得出圆的半径,利用它们的面积公式解答.
9.A
【分析】需要理解每个选项的含义,判断哪个选项描述了圆心到圆上的距离一样长。
【详解】A.“一中”指圆心,“同长”指圆心到圆上各点的距离相等,即描述了圆心到圆上的距离一样长。
B.此说法主要是阐述圆与方的生成关系,并非描述圆心到圆上的距离;
C.这是说圆的周长大约是直径的三倍,没有涉及圆心到圆上的距离;
D.这里的“规”和“矩”是指画图工具,不是直接描述圆心到圆上的距离;
描述圆心到圆上的距离一样长的是圆,一中同长也。
故答案为:A
10.B
【详解】略
11. 相等 相等 2倍
【详解】略
12.5
【分析】同一圆内,直径=半径×2,据此分析。
【详解】2.5×2=5(厘米)
【点睛】关键是熟悉圆的特征,掌握直径和半径的关系。
13. 8分米/8dm 10厘米/10cm 2.6米/2.6m
【分析】已知半径,求直径,根据“d=2r”求解;已知直径,求半径,根据“r=d÷2”求解。
【详解】5×2=10(厘米)
16÷2=8(分米)
1.3×2=2.6(米)
【点睛】此题应根据同圆或等圆中半径和直径之间的关系进行解答。
14. 4.5 360
【分析】由图可知,两个半径组成正方形的边长,用边长除以2即可求出半径长度;4个扇形的圆心角都是正方形的角,即都是90°,据此求解即可。
【详解】9÷2=4.5(厘米)
90°×4=360°
即这4个扇形的半径都是4.5厘米,它们的圆心角度数的和是360°。
【点睛】本题考查对扇形半径和圆心角的理解。
15.50
【分析】正方形内最大圆的直径是这个正方形的边长,圆心就是这个正方形的中心,由此可以作答。
【详解】由分析可得:在边长为50厘米的正方形内画一个最大的圆,它的直径是50厘米。
【点睛】此题考查了正方形和圆的特征,抓住正方形内最大圆的特点,是解决本题的关键。
16.(3π﹣6)平方厘米
【详解】试题分析:由图可知,该三角形为等腰直角三角形,所以三角形的底等于三角形的高,代出三角形的面积公式求出三角形的底,三角形的底就是半圆的直径,从而可以求出半圆的面积,最后用半圆的面积减去三角形面积的一半就是阴影部分的面积.
解:由图知,
S三角形=ah,
S三角形=a2,
12=a2,
a2=24(平方厘米),
S阴影=π﹣12÷2,
=π﹣12÷2,
=π﹣12÷2,
=3π﹣6(平方厘米),
故答案为(3π﹣6)平方厘米.
点评:此题考查了求组合图形的面积.
17.56cm
【详解】略
18. √ √ × √ ×
【分析】(1)含有等号的式子叫做等式;含有未知数的等式是方程;
(2)圆的半径的定义,即在同一个圆中,圆心到圆上的距离是半径;
(3)最简分数的定义是分子、分母只有公因数1的分数,或者说分子和分母互质的分数;
(4)根据分数乘法的意义,列出算式,解答后比较即可;
(5)真分数是指分子比分母小, 且分子与分母互质的分数,真分数比1小;假分数是指分子大于或等于分母的分数,即分数值大于或等于1的数,据此解答即可。
【详解】(1)因为,含有未知数的等式是方程,所以,等式不一定是方程,方程一定是等式。原题说法正确。
(2)在同一个圆中,圆心到圆上的距离是半径,在同一个圆里,半径都相等,所以,在同一个圆中,圆心到圆上的距离处处相等。原题说法正确。
(3)分母为8的最简真分数有、、、,共有4个,但分母为8的最简分数有无数个。原题说法错误。
(4)1×=(千克)
3×=(千克)
1千克的和3千克的相等。原题说法正确。
(5)1也是假分数,所以真分数都小于1,假分数大于或等于1。原题说法错误。
19.24649,31400,圆
【详解】试题分析:先根据正方形的周长公式:周长=边长×4,求出这个正方形的边长,再根据面积=边长×边长,求出它的面积;根据圆的周长公式C=2πr,求出圆的周长,再根据圆的面积公式S=πr2,求出圆的面积,再进行比较即可.
解:(1)628÷4=157(厘米),
157×157=24649(平方厘米),
(2)628÷3.14÷2=10(厘米),
3.14×102=31400(平方厘米),
31400>24649,
所以当正方形和圆的周长相等时圆的面积大;
答:这个正方形的面积是24649平方厘米,这个圆的面积是31400平方厘米,当正方形和圆的周长相等时圆的面积大;
故答案为24649,31400,圆.
点评:本题主要是利用正方形的周长公式、面积公式与圆的周长公式和面积公式解决问题.
20.
【详解】略
21.×
【详解】一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。如下图,根据扇形的意义可知,围成扇形的两条半径OA、0B必须经过弧AB的两端,不是任意的两条半径和一条弧就组成一个扇形,所以原题说法错误。
故答案为:×
22.×
【分析】依据轴对称图形的意义,即在同一个平面内,一个图形沿某条直线对折,对折后的两部分都能完全重合,则这个图形就是轴对称图形,这条直线就是其对称轴,从而可以画出它们的对称轴。
【详解】依据轴对称图形的意义,一个圆有无数条对称轴,半圆只有1条对称轴,原题说法错误。
故答案为:×
【点睛】解答此题的主要依据是:轴对称图形的意义及其特征。
23.√
【分析】根据顶点在圆心的角叫做圆心角,进行分析。
【详解】图中,∠1是圆心角,∠2也是圆心角,说法正确。
故答案为:√
24.×
【详解】求圆的面积和扇形面积都需要知道半径的大小,没有半径,则无法比较大小.
25.×
【分析】半圆的周长是圆周长的一半加上直径的长度,可画图进行对比,并由此判断即可。
【详解】半圆的周长如下图所示:
圆周长的一半,如图所示:
所以半圆的周长不等于圆周长的一半,原题说法错误。
故答案为:×
26.50.24 m
【分析】根据“S环形=π(R2-r2)”进行解答即可。
【详解】3.14×[5 -(6 ÷2) ]
=3.14×16
=50.24(m )
答:环形的面积是50.24m
27.30平方厘米,12.5平方厘米
【详解】试题分析:(1)观察图形可知,阴影部分的面积等于空白处三角形的面积等于这个长方形的面积的一半,据此即可解答;
(2)观察图形可知,阴影部分的面积是直角边长等于圆的半径的等腰直角三角形的面积,利用三角形的面积公式计算即可解答.
解:(1)10×6÷2=30(平方厘米),
答:阴影部分的面积是30平方厘米.
(2)10÷2=5(厘米),
5×5÷2=12.5(平方厘米),
答:阴影部分的面积是12.5平方厘米.
点评:此题考查组合图形的面积的计算方法,一般都是转化到规则图形中,利用面积公式进行计算.
28.,是顶点在圆心的角,是圆心角;
,顶点在圆上,不是圆心,不是圆心角;
,顶点在圆内,不是圆心,不是圆心角;
,是顶点在圆心的角,是圆心角。
【分析】顶点在圆心的角是圆心角,据此判断即可。
【详解】由分析可得:
,是顶点在圆心的角,是圆心角;
,顶点在圆上,不是圆心,不是圆心角;
,顶点在圆内,不是圆心,不是圆心角;
,是顶点在圆心的角,是圆心角。
【点睛】掌握圆心角的含义是此题的关键。
29.(1)不是
(2)见详解
【分析】(1)一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形;据此判断。
(2)根据扇形的意义,在圆中画出一个圆心角是60°的扇形即可。
【详解】(1)第一幅图阴影部分的两条线段不是圆的半径,所以亮亮画的不是扇形。
(2)如图:
(画法不唯一)
30.28.26平方米
【分析】由题意可知,就是求圆环的面积,大圆半径为8÷2+1,再根据进行解答即可。
【详解】8÷2+1
=4+1
=5(米);
8÷2=4(米);
3.14×(5 -4 )
=3.14×9
=28.26(平方米)
答:小路的面积是28.26平方米。
【点睛】明确本题是求圆环的面积是解答本题的关键。
31.如图
【详解】试题分析:根据圆的周长公式C=2πr可计算出这个圆的半径,然后再利用画圆的方法进行作图即可.
解:(1)圆的半径为:12.56÷3.14÷2=2(厘米),
(2)作图如下:
点评:此题主要考查的是圆的周长公式的应用和画圆的方法.
32.如图,3;2;小火车
【详解】试题分析:(1)正方形内最大的圆,就是以正方形的中心为圆心、边长为直径的圆,由此即可画出符合题意的圆;
(2)数对表示位置的方法是:第一个数字表示列,第二个数字表示行,由此即可解决问题.
解:(1)以正方形的中心为圆心、边长4厘米为直径画圆,如图即是正方形内最大的圆,
(2)根据数对表示位置的方法可得:小飞机在第3列、第2行,所以它的位置表示为:(3,2);
小李的位置是(5,4),即在第5列、第4行处,是小火车;
答:小飞机在地图上的位置是(3,2);现在小李的位置是(5,4),他正在玩小火车.
故答案为3;2;小火车.
点评:此题考查了正方形内最大圆的特点及画法;以及数对表示位置的方法的灵活应用.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第五单元圆
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.圆的面积与它的( )无关.
A.圆心 B.半径 C.周长
2.从圆心到圆上任意一点的线段叫做( )
A.直径 B.半径 C.直线
3.如图,盒子内刚好放下5瓶罐头,每瓶罐头瓶底的半径为3 cm,盒子的长为( )cm.
A.15 B.25 C.30 D.20
4.一座台钟,钟面上分针的长度是1dm,这根分针走60分钟,针尖走过的路程是( )dm。
A.3.14 B.6.28 C.37.68 D.12.56
5.一个圆的半径由3cm增加到8cm,则它的面积增加了( )cm2。
A.55 B.39 C.55π D.39π
6.圆形花坛的半径是3m,在花坛外侧铺一条1m宽的小路,小路的面积是( )m2。
A.21.98 B.50.24 C.15.7 D.3.14
7.环形的内圆半径为6厘米,外圆半径为8厘米,求环形面积的算式是( )。
A.3.14×62+3.14×82 B.3.14×(8-6)2 C.3.14×(82-62)
8.在一个正方形里画一个最大的圆,圆的面积是正方形面积的( )
A. B. C. D.π
9.在古代,我国数学史上关于圆的研究记载着不一样的说法,下面( )种说法是描述圆心到圆上的距离一样长。
A.圆,一中同长也 B.圆出于方,方出于矩
C.圆,径一而周三 D.没有规矩,不成方圆
10.下列图形中的角,是圆心角的个数是( ).
A.1个 B.2个 C.3个
二、填空题
11.在同一个圆或相等的圆中,所有的半径长度都( );所有的直径长度都( ).直径的长度是半径的( ).
12.如图,已知线段OA是圆的半径,那么线段BC的长度是( )厘米。
13.根据所给圆的信息填表。
半径 5厘米 ( ) 1.3米
直径 ( ) 16分米 ( )
14.这4个扇形的半径都是( )厘米,它们的圆心角度数的和是( )°。
15.在边长是50厘米的正方形内画一个最大的圆,圆的直径是( )厘米。
16.如图,直角三角形的面积是12平方厘米,则阴影部分的面积是 .(结果保留π)
17.如图所示大半圆内有三个小半圆,大半圆弧长为28cm,那么阴影部分图形的周长是 .
18.判断正误。
(1)等式不一定是方程,方程一定是等式。( )
(2)在同一个圆中,圆心到圆上的距离处处相等。( )
(3)分母为8的最简分数共有4个。( )
(4)1千克的和3千克的相等。( )
(5)真分数都小于1,假分数都大于1。( )
19.用628cm长的铁丝围成一个正方形,这个正方形的面积是 cm2,如果围成一个圆,这个圆的面积是 cm2.从上面的计算数据中我们发现,当正方形和圆的周长相等时, 的面积更大.
20.图中AB=BC=CD=3厘米,则以AB为直径的圆的周长是以AC为直径的圆的周长的( ),以AB为直径的圆的面积是以AD为直径的圆的面积的( ).
三、判断题
21.两条半径和一条弧就组成一个扇形。( )
22.圆有无数条对称轴,半圆也有无数条对称轴。( )
23.如图,∠1是圆心角,∠2也是圆心角。( )
24.扇形比圆小. ( )
25.半圆的周长等于圆周长的一半。( )
四、计算题
26.求环形的面积。
27.求下面各图形中阴影部分的面积.
五、解答题
28.判断下面各个角是不是圆心角,并说出理由。
29.操作。
(1)第一幅图阴影部分是亮亮画出的扇形。他画的是扇形吗?
(2)请你在圆中画出一个圆心角是60°的扇形。
30.一个花坛,直径8米,在它的周围有一条宽1米的环形小路,小路的面积是多少平方米?
31.画一个周长为12.56厘米的圆.
要求:(1)先计算
(2)作图规范.
32.画一画,填一填.
(1)在如图的正方形中画一个面积最大的圆.
(2)如图是儿童乐园的平面图.
①小飞机在地图上的位置是( , )
②现在小李的位置是(5,4),他正在玩 .
《第五单元圆》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A B C B C A C C A B
1.A
【分析】根据圆的面积公式S=π ,圆的面积与圆的半径有关,又因为d=2r、C=2πr所以圆的面积与它的直径和周长也有关系,圆心只能确定圆的位置,而不能确定圆的大小.
【详解】圆的面积公式:S=π ,π是一个固定值,圆的面积大小与它的半径有关,与它的圆心无关.
2.B
【详解】根据半径的含义可知:从圆心到圆上任意一点的线段叫做半径.
故选B.
3.C
【详解】3×10=30(cm)
故答案为C
一共有5个圆,长方形的长就是一个圆半径的10倍,由此计算即可.
4.B
【分析】分针走60分钟就是走了一个圆,这个圆的半径就是分针的长度,则针尖走过的路程就是圆的周长,圆的周长=,代入数据计算得出周长。
【详解】(dm)
针尖走过的路程是6.28dm。
故答案为:B
5.C
【分析】圆的面积公式为S=πr2,代入公式先算出半径为3cm时小圆的面积,再计算出半径为8cm时大圆的面积,然后用大圆面积减去小圆面积即可。
【详解】π×82-π×32
=π×64-π×9
=64π-9π
=55π(平方厘米)
所以,它的面积增加了55π平方厘米。
故答案为:C
6.A
【分析】小路的形状是个圆环,花坛半径是小圆半径,花坛半径+小路宽=大圆半径,根据圆环面积=圆周率×(大圆半径的平方-小圆半径的平方),列式计算即可。
【详解】3+1=4(m)
3.14×(42-32)
=3.14×(16-9)
=3.14×7
=21.98(m2)
小路的面积是21.98m2。
故答案为:A
7.C
【分析】根据环形的面积=π×(R -r ),R表示外圆的半径,r表示内圆的半径,据此即可解答。
【详解】环形的面积=π×(R -r )代入数据可得:3.14×(8 -6 )
故选:C。
【点睛】此题考查的是环形的面积公式,属于常考题型,需熟练掌握。
8.C
【详解】试题分析:设正方形的边长为2,则正方形内最大的圆的直径就是2,由此利用正方形和圆的面积公式解答即可.
解:设正方形的边长为2,则正方形内最大的圆的直径就是2,
则正方形的面积是:2×2=4;
圆的面积是:π=π;
所以圆的面积是正方形的面积的:π÷4=.
故选C.
点评:抓住正方形内最大圆的特点,设出正方形的边长,从而得出圆的半径,利用它们的面积公式解答.
9.A
【分析】需要理解每个选项的含义,判断哪个选项描述了圆心到圆上的距离一样长。
【详解】A.“一中”指圆心,“同长”指圆心到圆上各点的距离相等,即描述了圆心到圆上的距离一样长。
B.此说法主要是阐述圆与方的生成关系,并非描述圆心到圆上的距离;
C.这是说圆的周长大约是直径的三倍,没有涉及圆心到圆上的距离;
D.这里的“规”和“矩”是指画图工具,不是直接描述圆心到圆上的距离;
描述圆心到圆上的距离一样长的是圆,一中同长也。
故答案为:A
10.B
【详解】略
11. 相等 相等 2倍
【详解】略
12.5
【分析】同一圆内,直径=半径×2,据此分析。
【详解】2.5×2=5(厘米)
【点睛】关键是熟悉圆的特征,掌握直径和半径的关系。
13. 8分米/8dm 10厘米/10cm 2.6米/2.6m
【分析】已知半径,求直径,根据“d=2r”求解;已知直径,求半径,根据“r=d÷2”求解。
【详解】5×2=10(厘米)
16÷2=8(分米)
1.3×2=2.6(米)
【点睛】此题应根据同圆或等圆中半径和直径之间的关系进行解答。
14. 4.5 360
【分析】由图可知,两个半径组成正方形的边长,用边长除以2即可求出半径长度;4个扇形的圆心角都是正方形的角,即都是90°,据此求解即可。
【详解】9÷2=4.5(厘米)
90°×4=360°
即这4个扇形的半径都是4.5厘米,它们的圆心角度数的和是360°。
【点睛】本题考查对扇形半径和圆心角的理解。
15.50
【分析】正方形内最大圆的直径是这个正方形的边长,圆心就是这个正方形的中心,由此可以作答。
【详解】由分析可得:在边长为50厘米的正方形内画一个最大的圆,它的直径是50厘米。
【点睛】此题考查了正方形和圆的特征,抓住正方形内最大圆的特点,是解决本题的关键。
16.(3π﹣6)平方厘米
【详解】试题分析:由图可知,该三角形为等腰直角三角形,所以三角形的底等于三角形的高,代出三角形的面积公式求出三角形的底,三角形的底就是半圆的直径,从而可以求出半圆的面积,最后用半圆的面积减去三角形面积的一半就是阴影部分的面积.
解:由图知,
S三角形=ah,
S三角形=a2,
12=a2,
a2=24(平方厘米),
S阴影=π﹣12÷2,
=π﹣12÷2,
=π﹣12÷2,
=3π﹣6(平方厘米),
故答案为(3π﹣6)平方厘米.
点评:此题考查了求组合图形的面积.
17.56cm
【详解】略
18. √ √ × √ ×
【分析】(1)含有等号的式子叫做等式;含有未知数的等式是方程;
(2)圆的半径的定义,即在同一个圆中,圆心到圆上的距离是半径;
(3)最简分数的定义是分子、分母只有公因数1的分数,或者说分子和分母互质的分数;
(4)根据分数乘法的意义,列出算式,解答后比较即可;
(5)真分数是指分子比分母小, 且分子与分母互质的分数,真分数比1小;假分数是指分子大于或等于分母的分数,即分数值大于或等于1的数,据此解答即可。
【详解】(1)因为,含有未知数的等式是方程,所以,等式不一定是方程,方程一定是等式。原题说法正确。
(2)在同一个圆中,圆心到圆上的距离是半径,在同一个圆里,半径都相等,所以,在同一个圆中,圆心到圆上的距离处处相等。原题说法正确。
(3)分母为8的最简真分数有、、、,共有4个,但分母为8的最简分数有无数个。原题说法错误。
(4)1×=(千克)
3×=(千克)
1千克的和3千克的相等。原题说法正确。
(5)1也是假分数,所以真分数都小于1,假分数大于或等于1。原题说法错误。
19.24649,31400,圆
【详解】试题分析:先根据正方形的周长公式:周长=边长×4,求出这个正方形的边长,再根据面积=边长×边长,求出它的面积;根据圆的周长公式C=2πr,求出圆的周长,再根据圆的面积公式S=πr2,求出圆的面积,再进行比较即可.
解:(1)628÷4=157(厘米),
157×157=24649(平方厘米),
(2)628÷3.14÷2=10(厘米),
3.14×102=31400(平方厘米),
31400>24649,
所以当正方形和圆的周长相等时圆的面积大;
答:这个正方形的面积是24649平方厘米,这个圆的面积是31400平方厘米,当正方形和圆的周长相等时圆的面积大;
故答案为24649,31400,圆.
点评:本题主要是利用正方形的周长公式、面积公式与圆的周长公式和面积公式解决问题.
20.
【详解】略
21.×
【详解】一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。如下图,根据扇形的意义可知,围成扇形的两条半径OA、0B必须经过弧AB的两端,不是任意的两条半径和一条弧就组成一个扇形,所以原题说法错误。
故答案为:×
22.×
【分析】依据轴对称图形的意义,即在同一个平面内,一个图形沿某条直线对折,对折后的两部分都能完全重合,则这个图形就是轴对称图形,这条直线就是其对称轴,从而可以画出它们的对称轴。
【详解】依据轴对称图形的意义,一个圆有无数条对称轴,半圆只有1条对称轴,原题说法错误。
故答案为:×
【点睛】解答此题的主要依据是:轴对称图形的意义及其特征。
23.√
【分析】根据顶点在圆心的角叫做圆心角,进行分析。
【详解】图中,∠1是圆心角,∠2也是圆心角,说法正确。
故答案为:√
24.×
【详解】求圆的面积和扇形面积都需要知道半径的大小,没有半径,则无法比较大小.
25.×
【分析】半圆的周长是圆周长的一半加上直径的长度,可画图进行对比,并由此判断即可。
【详解】半圆的周长如下图所示:
圆周长的一半,如图所示:
所以半圆的周长不等于圆周长的一半,原题说法错误。
故答案为:×
26.50.24 m
【分析】根据“S环形=π(R2-r2)”进行解答即可。
【详解】3.14×[5 -(6 ÷2) ]
=3.14×16
=50.24(m )
答:环形的面积是50.24m
27.30平方厘米,12.5平方厘米
【详解】试题分析:(1)观察图形可知,阴影部分的面积等于空白处三角形的面积等于这个长方形的面积的一半,据此即可解答;
(2)观察图形可知,阴影部分的面积是直角边长等于圆的半径的等腰直角三角形的面积,利用三角形的面积公式计算即可解答.
解:(1)10×6÷2=30(平方厘米),
答:阴影部分的面积是30平方厘米.
(2)10÷2=5(厘米),
5×5÷2=12.5(平方厘米),
答:阴影部分的面积是12.5平方厘米.
点评:此题考查组合图形的面积的计算方法,一般都是转化到规则图形中,利用面积公式进行计算.
28.,是顶点在圆心的角,是圆心角;
,顶点在圆上,不是圆心,不是圆心角;
,顶点在圆内,不是圆心,不是圆心角;
,是顶点在圆心的角,是圆心角。
【分析】顶点在圆心的角是圆心角,据此判断即可。
【详解】由分析可得:
,是顶点在圆心的角,是圆心角;
,顶点在圆上,不是圆心,不是圆心角;
,顶点在圆内,不是圆心,不是圆心角;
,是顶点在圆心的角,是圆心角。
【点睛】掌握圆心角的含义是此题的关键。
29.(1)不是
(2)见详解
【分析】(1)一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形;据此判断。
(2)根据扇形的意义,在圆中画出一个圆心角是60°的扇形即可。
【详解】(1)第一幅图阴影部分的两条线段不是圆的半径,所以亮亮画的不是扇形。
(2)如图:
(画法不唯一)
30.28.26平方米
【分析】由题意可知,就是求圆环的面积,大圆半径为8÷2+1,再根据进行解答即可。
【详解】8÷2+1
=4+1
=5(米);
8÷2=4(米);
3.14×(5 -4 )
=3.14×9
=28.26(平方米)
答:小路的面积是28.26平方米。
【点睛】明确本题是求圆环的面积是解答本题的关键。
31.如图
【详解】试题分析:根据圆的周长公式C=2πr可计算出这个圆的半径,然后再利用画圆的方法进行作图即可.
解:(1)圆的半径为:12.56÷3.14÷2=2(厘米),
(2)作图如下:
点评:此题主要考查的是圆的周长公式的应用和画圆的方法.
32.如图,3;2;小火车
【详解】试题分析:(1)正方形内最大的圆,就是以正方形的中心为圆心、边长为直径的圆,由此即可画出符合题意的圆;
(2)数对表示位置的方法是:第一个数字表示列,第二个数字表示行,由此即可解决问题.
解:(1)以正方形的中心为圆心、边长4厘米为直径画圆,如图即是正方形内最大的圆,
(2)根据数对表示位置的方法可得:小飞机在第3列、第2行,所以它的位置表示为:(3,2);
小李的位置是(5,4),即在第5列、第4行处,是小火车;
答:小飞机在地图上的位置是(3,2);现在小李的位置是(5,4),他正在玩小火车.
故答案为3;2;小火车.
点评:此题考查了正方形内最大圆的特点及画法;以及数对表示位置的方法的灵活应用.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
