第一单元分数乘法同步练习(含解析)人教版数学六年级上册
文档属性
| 名称 | 第一单元分数乘法同步练习(含解析)人教版数学六年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 293.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-22 17:44:01 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第一单元分数乘法
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.×6的意义表述错误的是( )。
A.的6倍是多少 B.6个相乘是多少 C.6个相加是多少
2.在计算2.4×时,( )来计算比较简便。
A.化作分数 B.直接约分再算 C.化作小数
3.下列各数量关系中,把甲看作单位“1”的是( )。
A.乙的等于甲 B.甲的等于乙 C.甲是乙的
4.某工厂今年产量比去年多,今年的产量相当于去年的( )。
A. B. C.
5.一个班的人数增加后,又减少,现在的人数( )。
A.比原来多 B.比原来少 C.与原来同样多 D.无法确定
6.两施工队同修一条路,甲队第一天修了千米,乙队第一天修了全程的,已知这一天甲队比乙队修的少,那么这条路长( )
A.不足1千米 B.等于1千米 C.超过1千米
7.2022年4月1日,上海新增本土新冠肺炎确诊病例994例,其中的病例在黄浦区,黄浦区这些病例中是青壮年。当日,黄浦区确诊病例中青壮年有( )例。
A.84 B.126 C.56
8.的是( )。
A. B. C.4 D.16
9.表示求35的十分之七是多少?列算式是( )
A.35×0.7 B.35×7 C.35×70
10.如图是由面积都是5平方厘米的8个三角形组成,图中阴影部分的面积是多少平方厘米?列式是( )
A.8+8× B.5+5× C.5×8× D.××
二、填空题
11.+++ = ( )×( )
12.面粉的重量比大米多表示 。
13.“男生人数的相当于女生人数”,这句话中把( )看作单位“1”,等量关系是( )。
14.×7和7×它们的 相同, 不同。
15.20×表示的意义是( ).
×14表示的意义是( ).
×表示的意义是( ).
16.4米绳子平均分成9段,每段占全长的 ,每段 米.
17.一年中,大月的月份占;年有 个月。
18.的36倍是( ).
19.★×=○×(★、○为自然数),★与○比较,★ 于○.
20.一个皮球从16米的高处落下,每次着地后能反弹到原高度的一半再落下,当这个皮球第五次着地时,共经过了( )米。
三、判断题
21.8吨的的是1吨。( )
22.把一根长为1米的绳子平均分成5段,每段长1/5米.( )
23.一条绳子,已经用去了,还剩下米。( )
24.甲、乙两个班的男生人数各占本班人数的,则两个班的男生人数相等。( )
25.一杯纯果汁,小明先喝了半杯,觉得有些甜,就兑满了水,接着他又喝了杯,小明一共喝杯纯果汁和杯水。( )
四、计算题
26.根据线段图列式并计算。
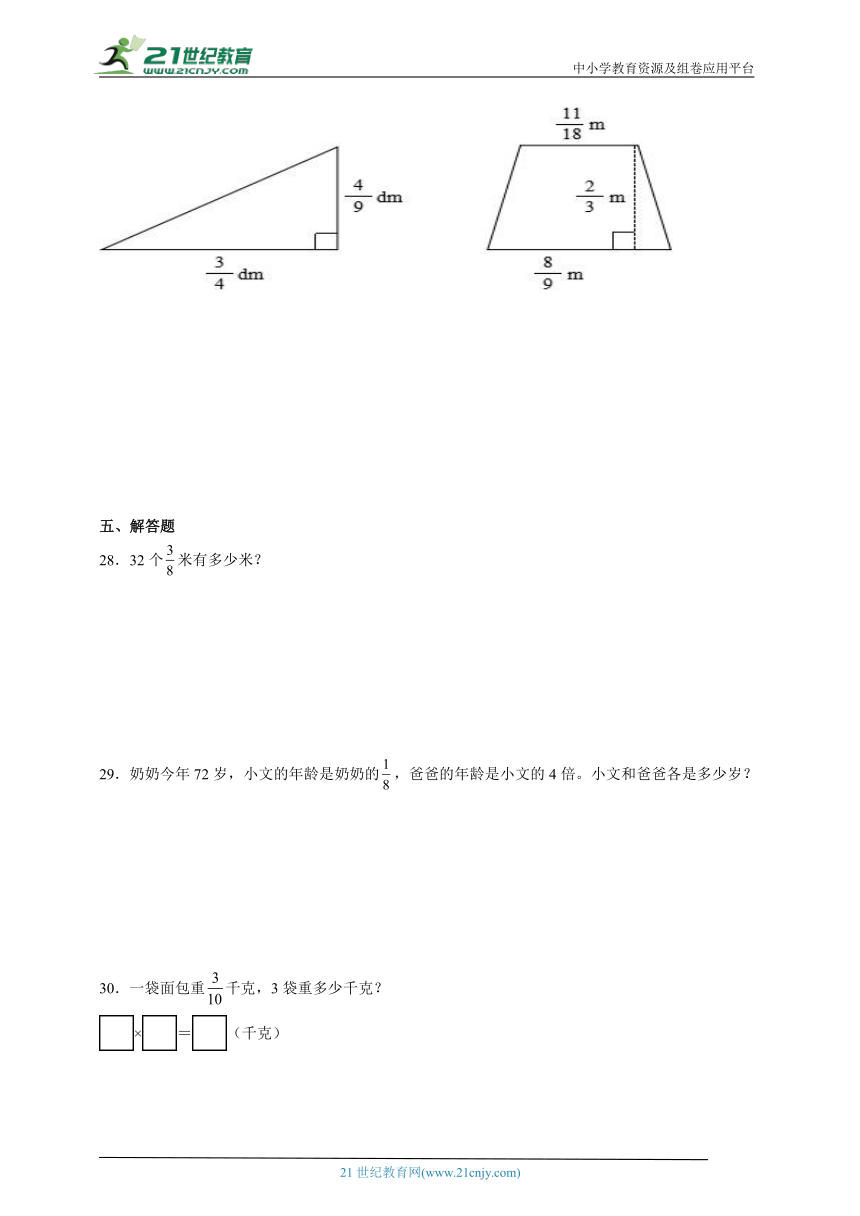
27.计算下面两个图形的面积。
五、解答题
28.32个米有多少米?
29.奶奶今年72岁,小文的年龄是奶奶的,爸爸的年龄是小文的4倍。小文和爸爸各是多少岁?
30.一袋面包重千克,3袋重多少千克?
×=(千克)
31.7月3是小聪的生日,妈妈买了一个大蛋糕,平均切成8块,小聪吃了2块,爸爸吃了3块,妈妈吃了1块.小聪家每个人各吃了这块蛋糕的几分之几?
32.直接写出得数.
=
.
《第一单元分数乘法》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B B B A B C C B A B
1.B
【分析】分数乘整数的乘法意义为表示求几个相同加数的和的运算。所以×6表示的6倍是多少或6个相加是多少。
【详解】根据分数乘整数的乘法意义可知:×6表示的6倍是多少或6个相加是多少。
故答案为:B
【点睛】分数乘整数的乘法的意义和整数乘法意义相同。
2.B
【分析】根据分数与小数乘法的计算法则:分数的分母与小数能约分的先约分,再计算;如果不能约分,把小数转换成分数,按分数乘分数的方法进行计算。
【详解】
在计算2.4×时,直接约分再算比较简便。
故答案为:B
【点睛】掌握分数与小数乘法的计算法则是解题的关键。
3.B
【分析】根据判断单位“1”的方法:一般是把“比、占、是、相当于”后面的量看作单位“1”,即分数“的”字前面的量看作单位“1”,进行解答即可.
【详解】A.乙的等于甲,是把乙看作单位“1”,所以不符合要求;
B.甲的等于乙,是把甲看作单位“1”,所以符合要求;
C.甲是乙的,是把乙看作单位“1”,所以不符合要求;
故选:B
【点睛】此题考查了判断单位“1”的方法,掌握判断单位“1”的方法:一般是把“比、占、是、相当于”后面的量看作单位“1”是解答此题的关键。
4.A
【分析】根据判断单位“1”的方法:一般是把“比、占、是、相当于”后面的量看作单位“1”,即分数“的”字前面的量看作单位“1”,进行解答即可。
【详解】某工厂今年产量比去年多,表示单位“1”的量是去年的产量,今年产量是去年的:1+=。
故选:A
【点睛】此题考查了判断单位“1”的方法,应灵活运用。
5.B
【分析】把原来的人数看成单位“1”,那么增加,也就是在单位“1”的基础上,增加单位“1”的,所以增加后是1+1×,也就是,减少是把增加之后的人数看成单位“1”,减少的,所以减少后是-,也就是,比1少,所以比原来少了。
【详解】1+1×
=1+
=
-
=
=
=
故答案为:B
【点睛】本题重点是能够区分清楚单位“1”。
6.C
【分析】这一天甲队比乙队修的少,即甲队修的千米小于全程的,由于1米的为1×=千米,所以,那么这条路长超过1千米。
【详解】由于1×=(千米),而千米<全程的,所以,那么这条路长超过1千米。
故选C。
【点睛】完成本题要注意前后两个所表示的意义是不同的,前一个表示的是具体的数量,后一个表示的是占全长的分率。
7.C
【分析】将上海新增本土新冠肺炎确诊病例看作单位“1”,上海新增本土新冠肺炎确诊病例×黄浦区对应分率=黄浦区新增病例;再将黄浦区新增病例看作单位“1”,黄浦区新增病例×青壮年对应分率=黄浦区确诊病例中青壮年例数,据此列式计算。
【详解】994××
=84×
=56(例)
当日,黄浦区确诊病例中青壮年有56例。
故答案为:C
8.B
【分析】求的是多少,用乘即可解答。
【详解】×=
的是。
故答案为:B
【点睛】熟练掌握分数与分数的乘法计算是解题的关键。
9.A
【分析】十分之七写成小数是0.7,计算一个数十分之七是多少,用乘法计算,依此即可选择。
【详解】由小数乘法的意义可得,表示求35的十分之七是多少的算式是:35×=35×0.7。
故答案为:A
10.B
【详解】试题分析:如图所示,三角形②的面积是5,而三角形①的面积是三角形②面积的一半,则阴影部分的面积是5+5×,据此解答即可.
解:如上图所示,三角形②的面积是5,而三角形①的面积是三角形②面积的一半,
则阴影部分的面积是5+5×,
故选B.
点评:将阴影部分进行分割,再据已知条件,即可求出阴影部分的面积.
11. 4
【解析】略
12.面粉比大米多的重量占大米的重量的
【分析】注意单位“1”的确定,单位“1”一般为“比、是、占”后边的量,据此求解。
【详解】(面粉的重量-大米的重量)÷大米的重量=,表示面粉比大米多的重量占大米的重量的。
【点睛】本题考查一个数比另一个数多(少)几分之几的意义。
13. 男生人数 男生人数×=女生人数
【分析】根据判断单位“1”的方法,一般是把分率“的”字前面的量看作单位“1”,或把“是、占、比”后面的量看作单位“1”。
已知“男生人数的相当于女生人数”,根据求一个数的几分之几是多少,用乘法计算,据此写出等量关系。
【详解】“男生人数的相当于女生人数”,这句话中把男生人数看作单位“1”,等量关系是男生人数×=女生人数。
【点睛】本题考查单位“1”的认识和确定以及分数乘法的意义。
14. 结果 意义
【分析】分数×整数,表示这个分数的几倍是多少;整数×分数,表示求这个整数的几分之几是多少,据此分析。
【详解】×7和7×它们的结果相同,意义不同。
【点睛】分数乘整数,分母不变,分子乘整数的积做分子,能约分要约分,也可以先约分,后计算。
15. 表示的求20的是多少. 表示的求14个相加的和是多少. 表示求的是多少.
【详解】略
16.,
【详解】试题分析:(1)4米绳子平均分成9段,求每段占全长的几分之几,就是把这根绳子的全长看作单位“1”,平均分为9份,求一份是全长的几分之几,用1÷9解答;
(2)求每段是多少米,用绳子的总长除以段数即可.
解:(1)每段占全长的:1÷9=;
(2)每段长:4÷9=(米);
故答案为,.
点评:解决此题关键是弄清求得是具体的数量还是分率,求具体的数量平均分的是具体的数量;求分率平均分的是单位“1”.
17.;9
【分析】(1)一年中,大月的月份有1月、3月、5月、7月、8月、10月、12月,共7个,用7除以12,即为大月的月份占几分之几。
(2)1年有12个月,年就有12×=9个月。
【详解】7÷12=;
12×=9(个月)。
所以一年中,大月的月份占,年有9个月。
18.21
【详解】略
19.>
【详解】试题分析:因为两个算式的积相等,一个因数大,另一个因数就小,由此判断即可.
解:=,
=,
<,
因为<,
★>○;
故答案为>.
点评:此题考查了分数乘法运算方法.
20.46
【分析】根据“每次着地后能反弹到原高度的一半再落下”,得出每次着地后能反弹的高度是原高度的,如此类推,得出每次着地后能反弹的高度,列式解答即可。
【详解】因为,16×=8(米),
8×=4(米),
4×=2(米),
2×=1(米),
所以共经过:16+8+8+4+4+2+2+1+1=46(米)。
【点睛】解答此题的关键是,根据题意,找出相应的量,列式解答即可。
21.√
【分析】根据求一个数的几分之几是多少用乘法,用8吨××,计算出结果即可。
【详解】8××=1(吨)
故答案为:√
【点睛】关键是理解分数乘法的意义,整体数量×部分对应分率=部分数量。
22.√
【详解】绳子平均分为5段,每一段占全长的,因此每一段的长度就是全长×=1×=(米).
23.×
【分析】把绳子的长度看作单位“1”,已经用去了,则说明剩下的占绳子总长的,因为单位“1”未知,所以不能求出剩下的长度。
【详解】1-=
因为单位“1”未知,所以无法求出对应的长度,所以题目中的结论是错误的。
故答案为:×
【点睛】解答本题的关键在于分清分数代表分率还是具体量。
24.×
【分析】求一个数的几分之几是多少用乘法计算,即一个数(单位“1”的量)×几分之几=部分量。据此可知:甲班的总人数×=甲班的男生人数,乙班的总人数×=乙班的男生人数。若甲、乙两班的总人数相等,则两个班的男生人数相等;若甲、乙两班的总人数不相等,则两个班的男生人数不相等。
【详解】因为不能确定甲、乙两个班的总人数是否相等,所以不能确定甲、乙两个班总人数的是否相等。即不能确定两个班的男生人数是否相等。原题说法错误。
故答案为:×
【点睛】解决分数问题关键是找准单位“1”,单位“1”不同,相同的分数对应的具体数量也不同。
25.√
【分析】把这杯果汁的量看作单位“1”,喝了半杯,即喝了杯纯果汁;兑满水,接着又喝了半杯,这时喝了纯果汁的杯的,即(×)杯,同理,也喝了(×)杯水。再把两次喝的果汁杯数相加。
【详解】+×
=+
=(杯)
×=(杯)
即,小明一共喝杯纯果汁和杯水,原题说法正确。
故答案为:√
26.24千米
【分析】把整个线段的总长度看作单位“1”,要求的线段长占总长度的,单位“1”已知,根据分数乘法的意义,求一个数的几分之几是多少,用乘法,用60乘即可得解。
【详解】(千米)
即线段图中要求的是24千米。
27.dm2;m2
【分析】根据三角形的面积公式S=ah,梯形的面积公式S=(a+b)h,分别代入数据计算求解。
【详解】(1)××
=×
=(dm2)
三角形的面积是dm2。
(2)(+)××
=(+)××
=××
=1×
=(m2)
梯形的面积是m2。
28.12米
【分析】就是求32个是多少,直接用32乘即可,能约分的要进行约分。
【详解】32×=12(米)
答:有12米。
【点睛】求一个数的几分之几是多少,用这个数×几分之几即可。
29.小文9岁,爸爸36岁
【分析】将奶奶的年龄看作单位“1”,将奶奶的年龄乘,先求出小文的年龄。求一个数的几倍是多少,将这个数乘倍数。那么将小文的年龄乘4,即可求出爸爸的年龄。
【详解】72×=9(岁)
9×4=36(岁)
答:小文9岁,爸爸36岁。
30.×3=
【分析】已知一袋面包重千克,求3袋面包的重量,根据乘法的意义,用一袋面包的重量乘3,即可求解。
【详解】×3=(千克)
答:3袋重千克。
【点睛】本题考查分数乘法的意义及应用,掌握分数乘整数的计算法则是解题的关键。
31.,,
【详解】试题分析:妈妈买了一个大蛋糕,平均切成8块,根据分数的意义可知,即将这块蛋糕当作单位“1”平均分成8份,小聪吃了2块,则吃了这块蛋糕的,爸爸吃了3块,即吃了这块蛋糕的,妈妈吃了1块,即吃了这块蛋糕的.
解:妈妈买了一个大蛋糕,平均切成8块,小聪吃了2块,爸爸吃了3块,妈妈吃了1块,
根据分数的意义可知,
小聪吃了这块蛋糕的,爸爸吃了蛋糕的,妈妈吃吃了这块蛋糕的.
故答案为,,.
点评:完成本题的依据为分数的意义,即将单位“1”平均分成若干份,表示这样一份或几份的数为分数.
32.=; ; ;
3; ; .
【详解】试题分析:根据分数乘法的计算法则,分子相乘的积作分子,分母相乘的积作分母,能约分的先约分计算简便.
点评:此题考查的目的是理解掌握分数乘法的计算法则,并且能够正确熟练地进行口算.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第一单元分数乘法
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.×6的意义表述错误的是( )。
A.的6倍是多少 B.6个相乘是多少 C.6个相加是多少
2.在计算2.4×时,( )来计算比较简便。
A.化作分数 B.直接约分再算 C.化作小数
3.下列各数量关系中,把甲看作单位“1”的是( )。
A.乙的等于甲 B.甲的等于乙 C.甲是乙的
4.某工厂今年产量比去年多,今年的产量相当于去年的( )。
A. B. C.
5.一个班的人数增加后,又减少,现在的人数( )。
A.比原来多 B.比原来少 C.与原来同样多 D.无法确定
6.两施工队同修一条路,甲队第一天修了千米,乙队第一天修了全程的,已知这一天甲队比乙队修的少,那么这条路长( )
A.不足1千米 B.等于1千米 C.超过1千米
7.2022年4月1日,上海新增本土新冠肺炎确诊病例994例,其中的病例在黄浦区,黄浦区这些病例中是青壮年。当日,黄浦区确诊病例中青壮年有( )例。
A.84 B.126 C.56
8.的是( )。
A. B. C.4 D.16
9.表示求35的十分之七是多少?列算式是( )
A.35×0.7 B.35×7 C.35×70
10.如图是由面积都是5平方厘米的8个三角形组成,图中阴影部分的面积是多少平方厘米?列式是( )
A.8+8× B.5+5× C.5×8× D.××
二、填空题
11.+++ = ( )×( )
12.面粉的重量比大米多表示 。
13.“男生人数的相当于女生人数”,这句话中把( )看作单位“1”,等量关系是( )。
14.×7和7×它们的 相同, 不同。
15.20×表示的意义是( ).
×14表示的意义是( ).
×表示的意义是( ).
16.4米绳子平均分成9段,每段占全长的 ,每段 米.
17.一年中,大月的月份占;年有 个月。
18.的36倍是( ).
19.★×=○×(★、○为自然数),★与○比较,★ 于○.
20.一个皮球从16米的高处落下,每次着地后能反弹到原高度的一半再落下,当这个皮球第五次着地时,共经过了( )米。
三、判断题
21.8吨的的是1吨。( )
22.把一根长为1米的绳子平均分成5段,每段长1/5米.( )
23.一条绳子,已经用去了,还剩下米。( )
24.甲、乙两个班的男生人数各占本班人数的,则两个班的男生人数相等。( )
25.一杯纯果汁,小明先喝了半杯,觉得有些甜,就兑满了水,接着他又喝了杯,小明一共喝杯纯果汁和杯水。( )
四、计算题
26.根据线段图列式并计算。
27.计算下面两个图形的面积。
五、解答题
28.32个米有多少米?
29.奶奶今年72岁,小文的年龄是奶奶的,爸爸的年龄是小文的4倍。小文和爸爸各是多少岁?
30.一袋面包重千克,3袋重多少千克?
×=(千克)
31.7月3是小聪的生日,妈妈买了一个大蛋糕,平均切成8块,小聪吃了2块,爸爸吃了3块,妈妈吃了1块.小聪家每个人各吃了这块蛋糕的几分之几?
32.直接写出得数.
=
.
《第一单元分数乘法》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B B B A B C C B A B
1.B
【分析】分数乘整数的乘法意义为表示求几个相同加数的和的运算。所以×6表示的6倍是多少或6个相加是多少。
【详解】根据分数乘整数的乘法意义可知:×6表示的6倍是多少或6个相加是多少。
故答案为:B
【点睛】分数乘整数的乘法的意义和整数乘法意义相同。
2.B
【分析】根据分数与小数乘法的计算法则:分数的分母与小数能约分的先约分,再计算;如果不能约分,把小数转换成分数,按分数乘分数的方法进行计算。
【详解】
在计算2.4×时,直接约分再算比较简便。
故答案为:B
【点睛】掌握分数与小数乘法的计算法则是解题的关键。
3.B
【分析】根据判断单位“1”的方法:一般是把“比、占、是、相当于”后面的量看作单位“1”,即分数“的”字前面的量看作单位“1”,进行解答即可.
【详解】A.乙的等于甲,是把乙看作单位“1”,所以不符合要求;
B.甲的等于乙,是把甲看作单位“1”,所以符合要求;
C.甲是乙的,是把乙看作单位“1”,所以不符合要求;
故选:B
【点睛】此题考查了判断单位“1”的方法,掌握判断单位“1”的方法:一般是把“比、占、是、相当于”后面的量看作单位“1”是解答此题的关键。
4.A
【分析】根据判断单位“1”的方法:一般是把“比、占、是、相当于”后面的量看作单位“1”,即分数“的”字前面的量看作单位“1”,进行解答即可。
【详解】某工厂今年产量比去年多,表示单位“1”的量是去年的产量,今年产量是去年的:1+=。
故选:A
【点睛】此题考查了判断单位“1”的方法,应灵活运用。
5.B
【分析】把原来的人数看成单位“1”,那么增加,也就是在单位“1”的基础上,增加单位“1”的,所以增加后是1+1×,也就是,减少是把增加之后的人数看成单位“1”,减少的,所以减少后是-,也就是,比1少,所以比原来少了。
【详解】1+1×
=1+
=
-
=
=
=
故答案为:B
【点睛】本题重点是能够区分清楚单位“1”。
6.C
【分析】这一天甲队比乙队修的少,即甲队修的千米小于全程的,由于1米的为1×=千米,所以,那么这条路长超过1千米。
【详解】由于1×=(千米),而千米<全程的,所以,那么这条路长超过1千米。
故选C。
【点睛】完成本题要注意前后两个所表示的意义是不同的,前一个表示的是具体的数量,后一个表示的是占全长的分率。
7.C
【分析】将上海新增本土新冠肺炎确诊病例看作单位“1”,上海新增本土新冠肺炎确诊病例×黄浦区对应分率=黄浦区新增病例;再将黄浦区新增病例看作单位“1”,黄浦区新增病例×青壮年对应分率=黄浦区确诊病例中青壮年例数,据此列式计算。
【详解】994××
=84×
=56(例)
当日,黄浦区确诊病例中青壮年有56例。
故答案为:C
8.B
【分析】求的是多少,用乘即可解答。
【详解】×=
的是。
故答案为:B
【点睛】熟练掌握分数与分数的乘法计算是解题的关键。
9.A
【分析】十分之七写成小数是0.7,计算一个数十分之七是多少,用乘法计算,依此即可选择。
【详解】由小数乘法的意义可得,表示求35的十分之七是多少的算式是:35×=35×0.7。
故答案为:A
10.B
【详解】试题分析:如图所示,三角形②的面积是5,而三角形①的面积是三角形②面积的一半,则阴影部分的面积是5+5×,据此解答即可.
解:如上图所示,三角形②的面积是5,而三角形①的面积是三角形②面积的一半,
则阴影部分的面积是5+5×,
故选B.
点评:将阴影部分进行分割,再据已知条件,即可求出阴影部分的面积.
11. 4
【解析】略
12.面粉比大米多的重量占大米的重量的
【分析】注意单位“1”的确定,单位“1”一般为“比、是、占”后边的量,据此求解。
【详解】(面粉的重量-大米的重量)÷大米的重量=,表示面粉比大米多的重量占大米的重量的。
【点睛】本题考查一个数比另一个数多(少)几分之几的意义。
13. 男生人数 男生人数×=女生人数
【分析】根据判断单位“1”的方法,一般是把分率“的”字前面的量看作单位“1”,或把“是、占、比”后面的量看作单位“1”。
已知“男生人数的相当于女生人数”,根据求一个数的几分之几是多少,用乘法计算,据此写出等量关系。
【详解】“男生人数的相当于女生人数”,这句话中把男生人数看作单位“1”,等量关系是男生人数×=女生人数。
【点睛】本题考查单位“1”的认识和确定以及分数乘法的意义。
14. 结果 意义
【分析】分数×整数,表示这个分数的几倍是多少;整数×分数,表示求这个整数的几分之几是多少,据此分析。
【详解】×7和7×它们的结果相同,意义不同。
【点睛】分数乘整数,分母不变,分子乘整数的积做分子,能约分要约分,也可以先约分,后计算。
15. 表示的求20的是多少. 表示的求14个相加的和是多少. 表示求的是多少.
【详解】略
16.,
【详解】试题分析:(1)4米绳子平均分成9段,求每段占全长的几分之几,就是把这根绳子的全长看作单位“1”,平均分为9份,求一份是全长的几分之几,用1÷9解答;
(2)求每段是多少米,用绳子的总长除以段数即可.
解:(1)每段占全长的:1÷9=;
(2)每段长:4÷9=(米);
故答案为,.
点评:解决此题关键是弄清求得是具体的数量还是分率,求具体的数量平均分的是具体的数量;求分率平均分的是单位“1”.
17.;9
【分析】(1)一年中,大月的月份有1月、3月、5月、7月、8月、10月、12月,共7个,用7除以12,即为大月的月份占几分之几。
(2)1年有12个月,年就有12×=9个月。
【详解】7÷12=;
12×=9(个月)。
所以一年中,大月的月份占,年有9个月。
18.21
【详解】略
19.>
【详解】试题分析:因为两个算式的积相等,一个因数大,另一个因数就小,由此判断即可.
解:=,
=,
<,
因为<,
★>○;
故答案为>.
点评:此题考查了分数乘法运算方法.
20.46
【分析】根据“每次着地后能反弹到原高度的一半再落下”,得出每次着地后能反弹的高度是原高度的,如此类推,得出每次着地后能反弹的高度,列式解答即可。
【详解】因为,16×=8(米),
8×=4(米),
4×=2(米),
2×=1(米),
所以共经过:16+8+8+4+4+2+2+1+1=46(米)。
【点睛】解答此题的关键是,根据题意,找出相应的量,列式解答即可。
21.√
【分析】根据求一个数的几分之几是多少用乘法,用8吨××,计算出结果即可。
【详解】8××=1(吨)
故答案为:√
【点睛】关键是理解分数乘法的意义,整体数量×部分对应分率=部分数量。
22.√
【详解】绳子平均分为5段,每一段占全长的,因此每一段的长度就是全长×=1×=(米).
23.×
【分析】把绳子的长度看作单位“1”,已经用去了,则说明剩下的占绳子总长的,因为单位“1”未知,所以不能求出剩下的长度。
【详解】1-=
因为单位“1”未知,所以无法求出对应的长度,所以题目中的结论是错误的。
故答案为:×
【点睛】解答本题的关键在于分清分数代表分率还是具体量。
24.×
【分析】求一个数的几分之几是多少用乘法计算,即一个数(单位“1”的量)×几分之几=部分量。据此可知:甲班的总人数×=甲班的男生人数,乙班的总人数×=乙班的男生人数。若甲、乙两班的总人数相等,则两个班的男生人数相等;若甲、乙两班的总人数不相等,则两个班的男生人数不相等。
【详解】因为不能确定甲、乙两个班的总人数是否相等,所以不能确定甲、乙两个班总人数的是否相等。即不能确定两个班的男生人数是否相等。原题说法错误。
故答案为:×
【点睛】解决分数问题关键是找准单位“1”,单位“1”不同,相同的分数对应的具体数量也不同。
25.√
【分析】把这杯果汁的量看作单位“1”,喝了半杯,即喝了杯纯果汁;兑满水,接着又喝了半杯,这时喝了纯果汁的杯的,即(×)杯,同理,也喝了(×)杯水。再把两次喝的果汁杯数相加。
【详解】+×
=+
=(杯)
×=(杯)
即,小明一共喝杯纯果汁和杯水,原题说法正确。
故答案为:√
26.24千米
【分析】把整个线段的总长度看作单位“1”,要求的线段长占总长度的,单位“1”已知,根据分数乘法的意义,求一个数的几分之几是多少,用乘法,用60乘即可得解。
【详解】(千米)
即线段图中要求的是24千米。
27.dm2;m2
【分析】根据三角形的面积公式S=ah,梯形的面积公式S=(a+b)h,分别代入数据计算求解。
【详解】(1)××
=×
=(dm2)
三角形的面积是dm2。
(2)(+)××
=(+)××
=××
=1×
=(m2)
梯形的面积是m2。
28.12米
【分析】就是求32个是多少,直接用32乘即可,能约分的要进行约分。
【详解】32×=12(米)
答:有12米。
【点睛】求一个数的几分之几是多少,用这个数×几分之几即可。
29.小文9岁,爸爸36岁
【分析】将奶奶的年龄看作单位“1”,将奶奶的年龄乘,先求出小文的年龄。求一个数的几倍是多少,将这个数乘倍数。那么将小文的年龄乘4,即可求出爸爸的年龄。
【详解】72×=9(岁)
9×4=36(岁)
答:小文9岁,爸爸36岁。
30.×3=
【分析】已知一袋面包重千克,求3袋面包的重量,根据乘法的意义,用一袋面包的重量乘3,即可求解。
【详解】×3=(千克)
答:3袋重千克。
【点睛】本题考查分数乘法的意义及应用,掌握分数乘整数的计算法则是解题的关键。
31.,,
【详解】试题分析:妈妈买了一个大蛋糕,平均切成8块,根据分数的意义可知,即将这块蛋糕当作单位“1”平均分成8份,小聪吃了2块,则吃了这块蛋糕的,爸爸吃了3块,即吃了这块蛋糕的,妈妈吃了1块,即吃了这块蛋糕的.
解:妈妈买了一个大蛋糕,平均切成8块,小聪吃了2块,爸爸吃了3块,妈妈吃了1块,
根据分数的意义可知,
小聪吃了这块蛋糕的,爸爸吃了蛋糕的,妈妈吃吃了这块蛋糕的.
故答案为,,.
点评:完成本题的依据为分数的意义,即将单位“1”平均分成若干份,表示这样一份或几份的数为分数.
32.=; ; ;
3; ; .
【详解】试题分析:根据分数乘法的计算法则,分子相乘的积作分子,分母相乘的积作分母,能约分的先约分计算简便.
点评:此题考查的目的是理解掌握分数乘法的计算法则,并且能够正确熟练地进行口算.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
