23.1 第2课时 旋转作图 教案(表格式)2025-2026学年度人教版数学九年级上册
文档属性
| 名称 | 23.1 第2课时 旋转作图 教案(表格式)2025-2026学年度人教版数学九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 536.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-23 09:00:12 | ||
图片预览


文档简介
九年级上册教案
23.1 图形的旋转
第 2 课时 旋转作图
教学内容 第 2 课时 旋转作图 课时 1
核心素养目标 会用数学的眼光观察世界:经历观察、操作、猜想、验证、类比的过程,进一步积累数学活动经验,增强动手实践能力,发展空间观念. 会用数学的思维思考问题:通过具体图形旋转研究活动,激发好奇心和求知欲,树立学好数学的自信心,养成独立思考、合作交流等学习习惯. 会用数学的语言表达思想:掌握旋转及其运用,培养应用意识,能应用旋转的知识设计图案.
知识目标 1.复习掌握旋转及旋转作图的概念及基本性质. 2.能够根据旋转的基本性质解决实际问题和进行简单作图.
教学重点 掌握旋转及旋转作图的概念及基本性质.
教学难点 能够根据旋转的基本性质解决实际问题和进行简单作图.
教学准备 课件
教学过程 主要师生活动 设计意图
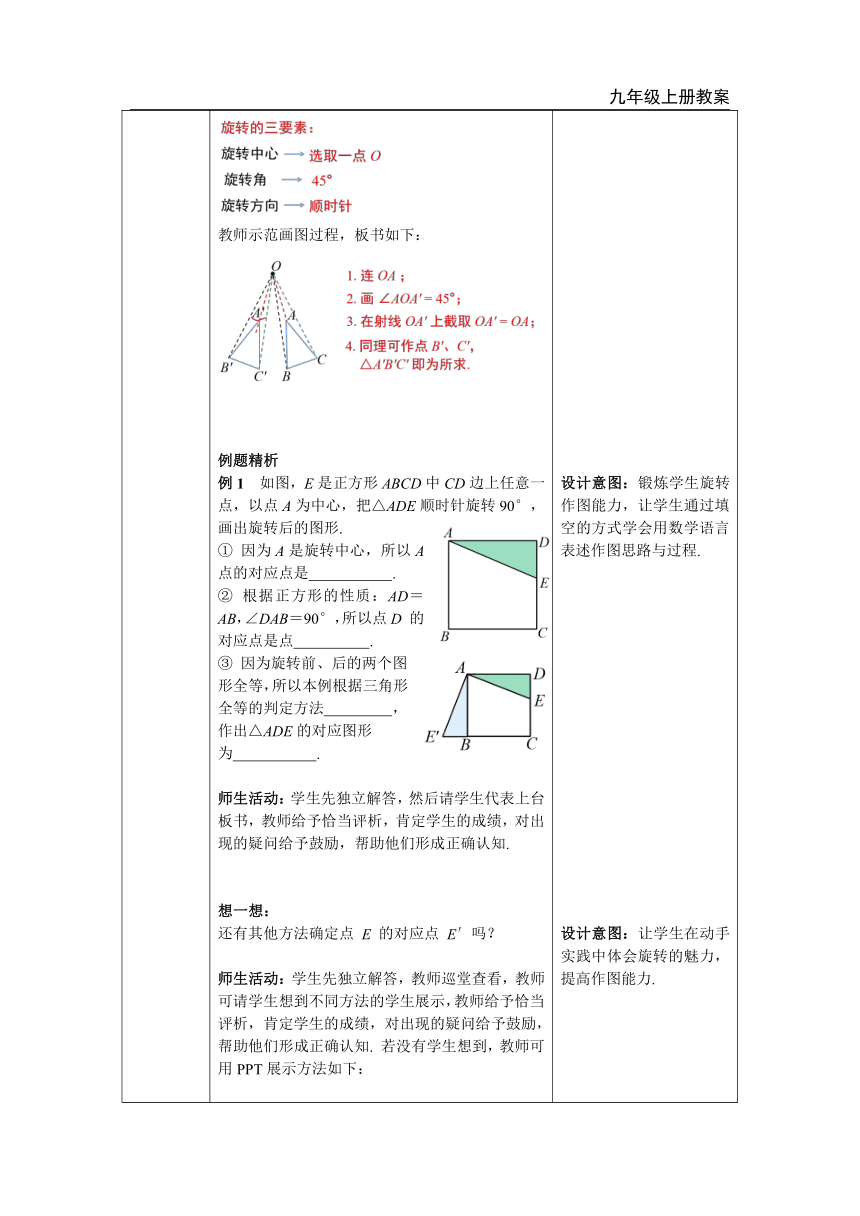
一、新课导入 二、探究新知 当堂练习 一、新课导入 → 师生活动:教师通过多媒体展示方块落下的方式,学生应能很快发现变换方式为平移. 活动:如何将右图旋转才能最终平移到空缺中呢? 学生积极思考,教师由此引出后面的活动探究. 二、探究新知 知识点1: 简单的旋转作图 活动探究 活动:画出△ABC 顺时针旋转 45° 的图形. 师生活动:教师引导学生回忆旋转的三要素,并说出本题对应的三要素是什么. 学生积极发言,教师整理板书: 教师示范画图过程,板书如下: 例题精析 例1 如图,E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形. ① 因为A是旋转中心,所以A 点的对应点是 . ② 根据正方形的性质:AD=AB,∠DAB=90°,所以点D 的对应点是点 . ③ 因为旋转前、后的两个图形全等,所以本例根据三角形全等的判定方法 ,作出△ADE的对应图形为 . 师生活动:学生先独立解答,然后请学生代表上台板书,教师给予恰当评析,肯定学生的成绩,对出现的疑问给予鼓励,帮助他们形成正确认知. 想一想: 还有其他方法确定点 E 的对应点 E′吗? 师生活动:学生先独立解答,教师巡堂查看,教师可请学生想到不同方法的学生展示,教师给予恰当评析,肯定学生的成绩,对出现的疑问给予鼓励,帮助他们形成正确认知. 若没有学生想到,教师可用PPT展示方法如下: 答:延长 CB,以点 A 为圆心,AE 的长为半径画弧,交CB的延长线于 E',连接 AE',则△ABE' 为旋转后的图形. 归纳总结: 旋转作图的基本步骤: (1) 明确旋转三要素: 旋转中心、旋转角和旋转方向. 找出关键点; 作出关键点的对应点; 作出新图形; 写出结论. 画一画 任意画一个△ABC,以 AC 中点为中心,把这个三角形旋转 180°. 师生活动:学生先独立解答,然后请学生展示画图过程及结果,教师给予恰当评析,肯定学生的成绩,对出现的疑问给予鼓励,帮助他们形成正确认知. 链接中考 1. (枣庄) 如图,将 △ABC 先向右平移1个单位,再绕点P按顺时针方向旋转90°得到△A'B'C' 则点 B 的对应点 B' 的坐标是( ) A.(4,0) B.(2,-2) C.(4,-1) D.(2,-3) 师生活动:学生先独立解答,然后请学生回答,教师给予恰当评析,肯定学生的成绩,对出现的疑问给予鼓励,帮助他们形成正确认知. 归纳总结: 平移与旋转相同与不同点: ① 相同:都是一种运动; 运动前后不改变图形的形状和大小. ② 不同: 师生活动:学生小组讨论,小组代表发言,师生共同总结出平移与旋转相同与不同点. 知识点2: 简单的旋转作图 观察课本上图案的变换过程,它们分别是改变旋转中的哪些要素旋转而成的? (1) _________不变,______改变,产生不同的旋转效果. (2) _______不变,________改变,产生不同的旋转效果. 师生活动:学生先独立思考,然后请学生代表回答,教师给予恰当评析,肯定学生的成绩,对出现的疑问给予鼓励,帮助他们形成正确认知. 2. 我们可以借助旋转可以设计出许多美丽的图案. 我们知道图形旋转 360°与原图重合,那么图(4)至少旋转多少度与原图形重合? 师生活动:教师出示图片和问题,学生独立思考,教师引导学生分析问题并得出答案. 正n边形的旋转特性 教师:类比正六边形,请同学们思考至少旋转多少度与原图形重合? 预测学生经过思考计算可得出答案,教师整理板书并引导学生总结: 归纳总结 链接中考 (镇江) 点 O 是正五边形 ABCDE 的中心,分别以各边为直径向正五边形的外部作半圆,组成了一幅美丽的图案(如图),这个图案绕点 O 至少旋转______° 后能与原来的图案互相重合. 师生活动:学生独立思考,学生代表回答,教师适当引导并给予正向评价. 三、当堂练习 1. 如图,是由一个矩形沿顺时针方向旋转 90° 后所形成的图形是( ) A. (1)(3) B. (2)(3) C. (1)(2) D. (3) 2. 等边三角形绕着它的中心 O 旋转,若旋转后的三角形能与自身重合,则旋转角最小是( ) A.360° B.240° C.120° D.60° 3. 如图,在平面直角坐标系中,已知△ABC 的顶点 A 的坐标为 (-1,2). (1) 将△ABC向右平移3个单位得到△DEF,请在图中画出平移后的图形; (2) 将△ABC 绕点 C 按逆时针方向旋转 90°后得到△MNC,请在图中画出旋转后的图形,并写出点 M,N 的坐标. 4. 给你如图所示的图形,请你旋转和平移设计出你喜欢的图案?(答案不唯一) 设计意图:以游戏的方式导入,增添课堂趣味性,引发学生思考,激发学习兴趣. 设计意图:本题为画图题,能帮助学生快速回忆上节课关于旋转三要素的知识点,也能快速进入本节课探究,起到衔接作用. 教师可在这题较为详细的展示画图步骤,让学生有样可依,提高学生的作图能力. 设计意图:锻炼学生旋转作图能力,让学生通过填空的方式学会用数学语言表述作图思路与过程. 设计意图:让学生在动手实践中体会旋转的魅力,提高作图能力. 设计意图:通过练习锻炼学生的作图能力. 设计意图:锻炼学生的作图能力,发展几何直观,提高解题技巧. 设计意图:引导学生及时总结前面具体问题得到的结论,梳理得到结论的过程,归纳出平移与旋转相同与不同点,构造完整的知识体系. 设计意图:改变旋转三要素的一个要素,让学生直观感受图案的变化,体会三要素对图片变化的影响,教会学生用数学的眼光发现图案的设计,发展几何直观. 设计意图:展示美丽图案,将美育融合进课堂,并引出正n边形的旋转特性的探究. 设计意图:从个例延申得出引出正n边形的旋转特性一般规律,发展抽象意识,并让学生体会正多边形的奇妙. 设计意图:通过真题锻炼学生对引出正n边形的旋转特性的掌握. 设计意图:考察学生对旋转知识的掌握,发展空间想象力. 设计意图:考察学生对引出正n边形的旋转特性的掌握. 设计意图:考察学生对旋转知识的掌握,加强学生的作图能力. 设计意图:锻炼学生的作图能力,丰富想象力,提升审美水平.
板书设计 旋转作图 作旋转图形 设计图案
课后小结 教师与学生一起回顾本节课所学的主要内容,梳理并完善知识思维导图。
教学反思 在上一课时的基础上,本课时进一步研究简单的旋转画图及图形之间的变换关系. 因为前面有了坚实的理论基础,所以学生能够更好的理解旋转,从而顺利的掌握作图的方法.
23.1 图形的旋转
第 2 课时 旋转作图
教学内容 第 2 课时 旋转作图 课时 1
核心素养目标 会用数学的眼光观察世界:经历观察、操作、猜想、验证、类比的过程,进一步积累数学活动经验,增强动手实践能力,发展空间观念. 会用数学的思维思考问题:通过具体图形旋转研究活动,激发好奇心和求知欲,树立学好数学的自信心,养成独立思考、合作交流等学习习惯. 会用数学的语言表达思想:掌握旋转及其运用,培养应用意识,能应用旋转的知识设计图案.
知识目标 1.复习掌握旋转及旋转作图的概念及基本性质. 2.能够根据旋转的基本性质解决实际问题和进行简单作图.
教学重点 掌握旋转及旋转作图的概念及基本性质.
教学难点 能够根据旋转的基本性质解决实际问题和进行简单作图.
教学准备 课件
教学过程 主要师生活动 设计意图
一、新课导入 二、探究新知 当堂练习 一、新课导入 → 师生活动:教师通过多媒体展示方块落下的方式,学生应能很快发现变换方式为平移. 活动:如何将右图旋转才能最终平移到空缺中呢? 学生积极思考,教师由此引出后面的活动探究. 二、探究新知 知识点1: 简单的旋转作图 活动探究 活动:画出△ABC 顺时针旋转 45° 的图形. 师生活动:教师引导学生回忆旋转的三要素,并说出本题对应的三要素是什么. 学生积极发言,教师整理板书: 教师示范画图过程,板书如下: 例题精析 例1 如图,E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形. ① 因为A是旋转中心,所以A 点的对应点是 . ② 根据正方形的性质:AD=AB,∠DAB=90°,所以点D 的对应点是点 . ③ 因为旋转前、后的两个图形全等,所以本例根据三角形全等的判定方法 ,作出△ADE的对应图形为 . 师生活动:学生先独立解答,然后请学生代表上台板书,教师给予恰当评析,肯定学生的成绩,对出现的疑问给予鼓励,帮助他们形成正确认知. 想一想: 还有其他方法确定点 E 的对应点 E′吗? 师生活动:学生先独立解答,教师巡堂查看,教师可请学生想到不同方法的学生展示,教师给予恰当评析,肯定学生的成绩,对出现的疑问给予鼓励,帮助他们形成正确认知. 若没有学生想到,教师可用PPT展示方法如下: 答:延长 CB,以点 A 为圆心,AE 的长为半径画弧,交CB的延长线于 E',连接 AE',则△ABE' 为旋转后的图形. 归纳总结: 旋转作图的基本步骤: (1) 明确旋转三要素: 旋转中心、旋转角和旋转方向. 找出关键点; 作出关键点的对应点; 作出新图形; 写出结论. 画一画 任意画一个△ABC,以 AC 中点为中心,把这个三角形旋转 180°. 师生活动:学生先独立解答,然后请学生展示画图过程及结果,教师给予恰当评析,肯定学生的成绩,对出现的疑问给予鼓励,帮助他们形成正确认知. 链接中考 1. (枣庄) 如图,将 △ABC 先向右平移1个单位,再绕点P按顺时针方向旋转90°得到△A'B'C' 则点 B 的对应点 B' 的坐标是( ) A.(4,0) B.(2,-2) C.(4,-1) D.(2,-3) 师生活动:学生先独立解答,然后请学生回答,教师给予恰当评析,肯定学生的成绩,对出现的疑问给予鼓励,帮助他们形成正确认知. 归纳总结: 平移与旋转相同与不同点: ① 相同:都是一种运动; 运动前后不改变图形的形状和大小. ② 不同: 师生活动:学生小组讨论,小组代表发言,师生共同总结出平移与旋转相同与不同点. 知识点2: 简单的旋转作图 观察课本上图案的变换过程,它们分别是改变旋转中的哪些要素旋转而成的? (1) _________不变,______改变,产生不同的旋转效果. (2) _______不变,________改变,产生不同的旋转效果. 师生活动:学生先独立思考,然后请学生代表回答,教师给予恰当评析,肯定学生的成绩,对出现的疑问给予鼓励,帮助他们形成正确认知. 2. 我们可以借助旋转可以设计出许多美丽的图案. 我们知道图形旋转 360°与原图重合,那么图(4)至少旋转多少度与原图形重合? 师生活动:教师出示图片和问题,学生独立思考,教师引导学生分析问题并得出答案. 正n边形的旋转特性 教师:类比正六边形,请同学们思考至少旋转多少度与原图形重合? 预测学生经过思考计算可得出答案,教师整理板书并引导学生总结: 归纳总结 链接中考 (镇江) 点 O 是正五边形 ABCDE 的中心,分别以各边为直径向正五边形的外部作半圆,组成了一幅美丽的图案(如图),这个图案绕点 O 至少旋转______° 后能与原来的图案互相重合. 师生活动:学生独立思考,学生代表回答,教师适当引导并给予正向评价. 三、当堂练习 1. 如图,是由一个矩形沿顺时针方向旋转 90° 后所形成的图形是( ) A. (1)(3) B. (2)(3) C. (1)(2) D. (3) 2. 等边三角形绕着它的中心 O 旋转,若旋转后的三角形能与自身重合,则旋转角最小是( ) A.360° B.240° C.120° D.60° 3. 如图,在平面直角坐标系中,已知△ABC 的顶点 A 的坐标为 (-1,2). (1) 将△ABC向右平移3个单位得到△DEF,请在图中画出平移后的图形; (2) 将△ABC 绕点 C 按逆时针方向旋转 90°后得到△MNC,请在图中画出旋转后的图形,并写出点 M,N 的坐标. 4. 给你如图所示的图形,请你旋转和平移设计出你喜欢的图案?(答案不唯一) 设计意图:以游戏的方式导入,增添课堂趣味性,引发学生思考,激发学习兴趣. 设计意图:本题为画图题,能帮助学生快速回忆上节课关于旋转三要素的知识点,也能快速进入本节课探究,起到衔接作用. 教师可在这题较为详细的展示画图步骤,让学生有样可依,提高学生的作图能力. 设计意图:锻炼学生旋转作图能力,让学生通过填空的方式学会用数学语言表述作图思路与过程. 设计意图:让学生在动手实践中体会旋转的魅力,提高作图能力. 设计意图:通过练习锻炼学生的作图能力. 设计意图:锻炼学生的作图能力,发展几何直观,提高解题技巧. 设计意图:引导学生及时总结前面具体问题得到的结论,梳理得到结论的过程,归纳出平移与旋转相同与不同点,构造完整的知识体系. 设计意图:改变旋转三要素的一个要素,让学生直观感受图案的变化,体会三要素对图片变化的影响,教会学生用数学的眼光发现图案的设计,发展几何直观. 设计意图:展示美丽图案,将美育融合进课堂,并引出正n边形的旋转特性的探究. 设计意图:从个例延申得出引出正n边形的旋转特性一般规律,发展抽象意识,并让学生体会正多边形的奇妙. 设计意图:通过真题锻炼学生对引出正n边形的旋转特性的掌握. 设计意图:考察学生对旋转知识的掌握,发展空间想象力. 设计意图:考察学生对引出正n边形的旋转特性的掌握. 设计意图:考察学生对旋转知识的掌握,加强学生的作图能力. 设计意图:锻炼学生的作图能力,丰富想象力,提升审美水平.
板书设计 旋转作图 作旋转图形 设计图案
课后小结 教师与学生一起回顾本节课所学的主要内容,梳理并完善知识思维导图。
教学反思 在上一课时的基础上,本课时进一步研究简单的旋转画图及图形之间的变换关系. 因为前面有了坚实的理论基础,所以学生能够更好的理解旋转,从而顺利的掌握作图的方法.
同课章节目录
