24.1.2 垂直于弦的直径 教案(表格式)2025-2026学年度人教版数学九年级上册
文档属性
| 名称 | 24.1.2 垂直于弦的直径 教案(表格式)2025-2026学年度人教版数学九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-23 00:00:00 | ||
图片预览



文档简介
九年级上册教案
24.1 圆的有关性质
24.1.2 垂直于弦的直径
教学内容 24.1.2 垂直于弦的直径 课时 1
核心素养目标 1.掌握垂径定理,理解其探索和证明过程; 2.能初步运用垂径定理解决有关的计算和证明问题。 3.在研究过程中,进一步体验“实验一归纳一猜想一证明”的方法;在解题过程中,注重发散思维的培养,同一个问题会从不同的角度去分析解决.
知识目标 1.进一步认识圆是轴对称图形. 2.能利用圆的轴对称性,通过探索、归纳、验证得出垂直于弦的直径的性质和推论,并能应用它解决一些简单的计算、证明和作图问题. 3.认识垂径定理及推论在实际中的应用,会用添加辅助线的方法解决问题.
教学重点 掌握垂径定理及其推论,熟练运用垂径定理及其推论解决一些有关证明、计算的问题.
教学难点 垂径定理的证明及应用.
教学准备 课件
教学过程 主要师生活动 设计意图
一、情境导入 二、探究新知 当堂练习,巩固所学 一、创设情境,导入新知 地震造成小区的圆柱形供水管道损坏,现在工人师傅要为我们换管道,如图,他测量出管道有积水部分的最大深度是 2 cm,水面的宽度为 8 cm,这个工人师傅想了又想,也不知道该用多大的水管来替换,你能帮他解决这个问题吗 师生活动:同学们先讨论,然后带着疑问点开启今天课堂内容. 二、小组合作,探究概念和性质 知识点一:垂径定理及其推论 探究一:折一折 同学们,拿出一张圆形纸片,沿着圆的任意一条直径对折,重复做几次,会发现了什么呢? 圆的对称性:
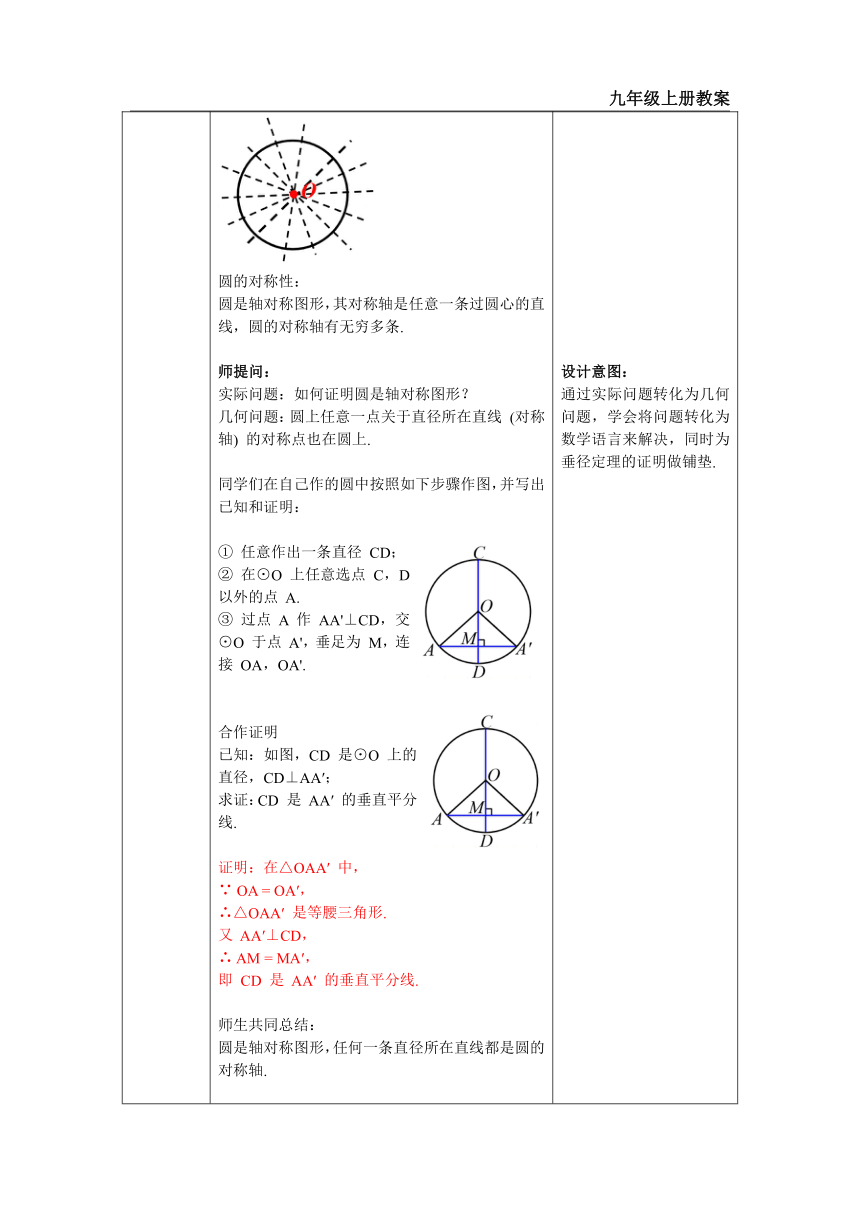
圆是轴对称图形,其对称轴是任意一条过圆心的直线,圆的对称轴有无穷多条. 师提问: 实际问题:如何证明圆是轴对称图形? 几何问题:圆上任意一点关于直径所在直线 (对称轴) 的对称点也在圆上. 同学们在自己作的圆中按照如下步骤作图,并写出已知和证明: ① 任意作出一条直径 CD; ② 在⊙O 上任意选点 C,D 以外的点 A. ③ 过点 A 作 AA'⊥CD,交⊙O 于点 A',垂足为 M,连接 OA,OA'. 合作证明 已知:如图,CD 是⊙O 上的直径,CD⊥AA′; 求证:CD 是 AA′ 的垂直平分线. 证明:在△OAA′ 中, ∵ OA = OA′, ∴△OAA′ 是等腰三角形. 又 AA′⊥CD, ∴ AM = MA′, 即 CD 是 AA′ 的垂直平分线. 师生共同总结: 圆是轴对称图形,任何一条直径所在直线都是圆的对称轴. 探究二:如图,AA′ 是⊙O 的一条弦,直径 CD⊥AA′, 垂足为 M. 你能发现图中有哪些相等的线段和劣弧 为什么 定义总结 垂径定理 垂直于弦的直径平分弦,并且平分弦所对的两条弧. 教师强调:两条弧:分别是劣弧、优弧 师提问:你能用几何语言表示吗? 推导格式: 想一想:下列图形是否具备垂径定理的条件?如果不是,请说明为什么? (1) (2) (3) (4) 答案:(1)是(2)不是,因为没有垂直. (3)是 (4)不是,因为 AB,CD 都不是直径. 典例精析 例1 如图,OE⊥AB 于 E,若⊙O 的半径为 10 cm,OE = 6 cm,则 AB = cm. 师生活动:教学时,给几分钟时间先让学生尝试着解决问题,在学生出现思维盲区时,教师给予详细分析,边讲边演示,在思维的激烈碰撞过程中,逐渐形成对垂径定理的认识. 思考探索 师提问:上述五个条件中的任何两个条件都可以推出其他三个结论吗? 证明猜想 证明举例 如图,AA′ 是⊙O 的一条弦,直径 CD 平分弦 AA′ 于点 M. (1)CD⊥AA′ 吗?为什么? 师生活动:让学生模仿圆的轴对称性质的证明过程,学生先独立思考,然后让学生分组讨论交流,并表述定理的内容——平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧. 教师展示解题过程 解:(1) 连接 AO、A′O,则 AO = A′O. 又∵ AM = A′M, ∴△AOM≌△A′OM(SSS). ∴∠AMO =∠A′MO = 90°. ∴ CD⊥AA′. (2) 由垂径定理可得 归纳总结 垂径定理的推论 平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧. 教师提问:“不是直径”这个条件能去掉吗? 如果不能,请举出反例. 师生活动:学生观察教师给出的定理的变式图形,以强化对定理基本图形的理解. 特别说明: 圆的两条直径是互相平分的. 师生共同总结: 垂径定理的本质是: 满足其中任两条,必定同时满足另三条 (1)一条直线过圆心 (2)这条直线垂直于弦 (3)这条直线平分不是直径的弦 (4)这条直线平分不是直径的弦所对的优弧 (5)这条直线平分不是直径的弦所对的劣弧 例3 赵州桥是我国隋代建造的石拱桥,距今约有 1400 年的历史,是我国古代人民勤劳与智慧的结晶.它的主桥拱是圆弧形,它的跨度(弧所对的弦的长)为 37 m,拱高(弧的中点到弦的距离)为 7.23 m,求赵州桥主桥拱的半径(结果保留 小数点后一位). 总结 垂径定理往往转化成应用勾股定理解直角三角形 练一练 1. 如图 a、b,一弓形弦长为 cm,弓形所在的圆的半径为 7 cm,则弓形的高为____cm. 2. 地震造成小区的圆柱形供水管道损坏,现在工人师傅要为我们换管道,如图,他测量出管道有积水部分的最大深度是 2 cm,水面的宽度为 8 cm,这个工人师傅想了又想,也不知道该用多大的水管来替换,你能帮他解决这个问题吗 解:过 O 作 OD⊥AB 于 D 交圆上于点 E.
由题意,得 DE = 2 cm,AB = 8 cm. ∵ OD⊥AB,∴ AD = DB = 4 cm. 设圆形水管半径为 r cm. 在 Rt△ODA 中,42 + (r - 2)2 = r2,即 r = 5 cm. 故应该用半径为 5 cm 的圆柱形水管替换. 三、当堂练习,巩固所学 1. 已知⊙O 中,弦 AB = 8 cm,圆心到 AB 的距离为 3 cm,则此圆的半径为 cm. 2.(分类讨论题)已知⊙O 的半径为 10 cm, 弦 MN ∥EF,且 MN = 12 cm,EF = 16 cm,则弦 MN 和EF 之间的距离为 cm. (朝阳区期末) 圆管涵是公路路基排水中常用的涵洞结构类型,它不仅力学性能好,且构造简单、施工方便.某水平放置的圆管涵圆柱形排水管道的截面是直径为 1 m 的圆,如图所示,若水面宽 AB = 0.8 m,求水的最大深度. 设计意图:创设现实问题情境,引导学生发现数学问题,不仅能很好地吸引学生注意力,还能让学生切身体会到生活中处处都时数学,感受数学美,了解知识的产生. 设计意图: 让学生通过动手实践来感受圆的轴对称性.通过回忆轴对称图形的性质,引导学生来证明圆是轴对称图形. 设计意图: 通过实际问题转化为几何问题,学会将问题转化为数学语言来解决,同时为垂径定理的证明做铺垫. 设计意图: 在对圆是轴对称图形证明的基础上,通过观察或者让学生折纸,体验垂径定理的形成过程,帮助学生分析垂径定理的条件和结论。同时又为学习推论作好准备. 设计意图:让学生经历了实验—观察—猜想—证明,学生的思维逐步被展开,现在可以引导学生证明并归纳定理,归纳定理时采用了文字语言和符号语言两种形式. 设计意图:强化对基本图形的理解,从特殊到一般,培养学对几何图形的化归思维能力。几何定理中文字语言、符号语言,图形语言的相互联系与转换也是学生应具备的能力。 设计意图:以垂径定理的图形为基本模型,根据实际问题的条件,建立数学几何模型,来解决赵州桥问题.让学生了解到:在圆中,解决有关弦的问题是,常常需要作“垂直于弦的直径”作为辅助线. 这种添加辅助线的方法需要不断强化,让学生真正掌握. 设计意图:加强对垂径定理的运用. 设计意图:本题是重径定理的应用,解题过程中使用了列方程的方法,用代数方法解决几何问题,这种思想应该向学生进行渗透,同时回扣了导入. 设计意图:课堂练习的设置由易到难,以不同的形式来强化学生对垂径定理的认识。从练习中归纳总结解题的方法,从而使学生掌握此类问题的解题方法和技巧
板书设计 24.1.2 垂直于弦的直径 垂径定理: 垂直于弦的直径平分弦,并且平分弦所对的两条弧. 垂径定理的推论: 平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
课后小结 教师与学生一起回顾本节课所学的主要内容,梳理并完善知识思维导图。
教学反思 垂径定理是中学数学中的一个很重要的定理,由于它涉及的条件结论比较多,学生容易搞混淆,本节课采取了讲练结合、动手操作的教学方法,课前布置所有同学制作一张圆形纸片,课上利用此纸片探索、体验圆是轴对称图形,并进一步利用圆的轴对称性探究垂径定理,环环相扣、逐层深入,激发学生的学习兴趣,收到了很好的教学效果.
24.1 圆的有关性质
24.1.2 垂直于弦的直径
教学内容 24.1.2 垂直于弦的直径 课时 1
核心素养目标 1.掌握垂径定理,理解其探索和证明过程; 2.能初步运用垂径定理解决有关的计算和证明问题。 3.在研究过程中,进一步体验“实验一归纳一猜想一证明”的方法;在解题过程中,注重发散思维的培养,同一个问题会从不同的角度去分析解决.
知识目标 1.进一步认识圆是轴对称图形. 2.能利用圆的轴对称性,通过探索、归纳、验证得出垂直于弦的直径的性质和推论,并能应用它解决一些简单的计算、证明和作图问题. 3.认识垂径定理及推论在实际中的应用,会用添加辅助线的方法解决问题.
教学重点 掌握垂径定理及其推论,熟练运用垂径定理及其推论解决一些有关证明、计算的问题.
教学难点 垂径定理的证明及应用.
教学准备 课件
教学过程 主要师生活动 设计意图
一、情境导入 二、探究新知 当堂练习,巩固所学 一、创设情境,导入新知 地震造成小区的圆柱形供水管道损坏,现在工人师傅要为我们换管道,如图,他测量出管道有积水部分的最大深度是 2 cm,水面的宽度为 8 cm,这个工人师傅想了又想,也不知道该用多大的水管来替换,你能帮他解决这个问题吗 师生活动:同学们先讨论,然后带着疑问点开启今天课堂内容. 二、小组合作,探究概念和性质 知识点一:垂径定理及其推论 探究一:折一折 同学们,拿出一张圆形纸片,沿着圆的任意一条直径对折,重复做几次,会发现了什么呢? 圆的对称性:
圆是轴对称图形,其对称轴是任意一条过圆心的直线,圆的对称轴有无穷多条. 师提问: 实际问题:如何证明圆是轴对称图形? 几何问题:圆上任意一点关于直径所在直线 (对称轴) 的对称点也在圆上. 同学们在自己作的圆中按照如下步骤作图,并写出已知和证明: ① 任意作出一条直径 CD; ② 在⊙O 上任意选点 C,D 以外的点 A. ③ 过点 A 作 AA'⊥CD,交⊙O 于点 A',垂足为 M,连接 OA,OA'. 合作证明 已知:如图,CD 是⊙O 上的直径,CD⊥AA′; 求证:CD 是 AA′ 的垂直平分线. 证明:在△OAA′ 中, ∵ OA = OA′, ∴△OAA′ 是等腰三角形. 又 AA′⊥CD, ∴ AM = MA′, 即 CD 是 AA′ 的垂直平分线. 师生共同总结: 圆是轴对称图形,任何一条直径所在直线都是圆的对称轴. 探究二:如图,AA′ 是⊙O 的一条弦,直径 CD⊥AA′, 垂足为 M. 你能发现图中有哪些相等的线段和劣弧 为什么 定义总结 垂径定理 垂直于弦的直径平分弦,并且平分弦所对的两条弧. 教师强调:两条弧:分别是劣弧、优弧 师提问:你能用几何语言表示吗? 推导格式: 想一想:下列图形是否具备垂径定理的条件?如果不是,请说明为什么? (1) (2) (3) (4) 答案:(1)是(2)不是,因为没有垂直. (3)是 (4)不是,因为 AB,CD 都不是直径. 典例精析 例1 如图,OE⊥AB 于 E,若⊙O 的半径为 10 cm,OE = 6 cm,则 AB = cm. 师生活动:教学时,给几分钟时间先让学生尝试着解决问题,在学生出现思维盲区时,教师给予详细分析,边讲边演示,在思维的激烈碰撞过程中,逐渐形成对垂径定理的认识. 思考探索 师提问:上述五个条件中的任何两个条件都可以推出其他三个结论吗? 证明猜想 证明举例 如图,AA′ 是⊙O 的一条弦,直径 CD 平分弦 AA′ 于点 M. (1)CD⊥AA′ 吗?为什么? 师生活动:让学生模仿圆的轴对称性质的证明过程,学生先独立思考,然后让学生分组讨论交流,并表述定理的内容——平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧. 教师展示解题过程 解:(1) 连接 AO、A′O,则 AO = A′O. 又∵ AM = A′M, ∴△AOM≌△A′OM(SSS). ∴∠AMO =∠A′MO = 90°. ∴ CD⊥AA′. (2) 由垂径定理可得 归纳总结 垂径定理的推论 平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧. 教师提问:“不是直径”这个条件能去掉吗? 如果不能,请举出反例. 师生活动:学生观察教师给出的定理的变式图形,以强化对定理基本图形的理解. 特别说明: 圆的两条直径是互相平分的. 师生共同总结: 垂径定理的本质是: 满足其中任两条,必定同时满足另三条 (1)一条直线过圆心 (2)这条直线垂直于弦 (3)这条直线平分不是直径的弦 (4)这条直线平分不是直径的弦所对的优弧 (5)这条直线平分不是直径的弦所对的劣弧 例3 赵州桥是我国隋代建造的石拱桥,距今约有 1400 年的历史,是我国古代人民勤劳与智慧的结晶.它的主桥拱是圆弧形,它的跨度(弧所对的弦的长)为 37 m,拱高(弧的中点到弦的距离)为 7.23 m,求赵州桥主桥拱的半径(结果保留 小数点后一位). 总结 垂径定理往往转化成应用勾股定理解直角三角形 练一练 1. 如图 a、b,一弓形弦长为 cm,弓形所在的圆的半径为 7 cm,则弓形的高为____cm. 2. 地震造成小区的圆柱形供水管道损坏,现在工人师傅要为我们换管道,如图,他测量出管道有积水部分的最大深度是 2 cm,水面的宽度为 8 cm,这个工人师傅想了又想,也不知道该用多大的水管来替换,你能帮他解决这个问题吗 解:过 O 作 OD⊥AB 于 D 交圆上于点 E.
由题意,得 DE = 2 cm,AB = 8 cm. ∵ OD⊥AB,∴ AD = DB = 4 cm. 设圆形水管半径为 r cm. 在 Rt△ODA 中,42 + (r - 2)2 = r2,即 r = 5 cm. 故应该用半径为 5 cm 的圆柱形水管替换. 三、当堂练习,巩固所学 1. 已知⊙O 中,弦 AB = 8 cm,圆心到 AB 的距离为 3 cm,则此圆的半径为 cm. 2.(分类讨论题)已知⊙O 的半径为 10 cm, 弦 MN ∥EF,且 MN = 12 cm,EF = 16 cm,则弦 MN 和EF 之间的距离为 cm. (朝阳区期末) 圆管涵是公路路基排水中常用的涵洞结构类型,它不仅力学性能好,且构造简单、施工方便.某水平放置的圆管涵圆柱形排水管道的截面是直径为 1 m 的圆,如图所示,若水面宽 AB = 0.8 m,求水的最大深度. 设计意图:创设现实问题情境,引导学生发现数学问题,不仅能很好地吸引学生注意力,还能让学生切身体会到生活中处处都时数学,感受数学美,了解知识的产生. 设计意图: 让学生通过动手实践来感受圆的轴对称性.通过回忆轴对称图形的性质,引导学生来证明圆是轴对称图形. 设计意图: 通过实际问题转化为几何问题,学会将问题转化为数学语言来解决,同时为垂径定理的证明做铺垫. 设计意图: 在对圆是轴对称图形证明的基础上,通过观察或者让学生折纸,体验垂径定理的形成过程,帮助学生分析垂径定理的条件和结论。同时又为学习推论作好准备. 设计意图:让学生经历了实验—观察—猜想—证明,学生的思维逐步被展开,现在可以引导学生证明并归纳定理,归纳定理时采用了文字语言和符号语言两种形式. 设计意图:强化对基本图形的理解,从特殊到一般,培养学对几何图形的化归思维能力。几何定理中文字语言、符号语言,图形语言的相互联系与转换也是学生应具备的能力。 设计意图:以垂径定理的图形为基本模型,根据实际问题的条件,建立数学几何模型,来解决赵州桥问题.让学生了解到:在圆中,解决有关弦的问题是,常常需要作“垂直于弦的直径”作为辅助线. 这种添加辅助线的方法需要不断强化,让学生真正掌握. 设计意图:加强对垂径定理的运用. 设计意图:本题是重径定理的应用,解题过程中使用了列方程的方法,用代数方法解决几何问题,这种思想应该向学生进行渗透,同时回扣了导入. 设计意图:课堂练习的设置由易到难,以不同的形式来强化学生对垂径定理的认识。从练习中归纳总结解题的方法,从而使学生掌握此类问题的解题方法和技巧
板书设计 24.1.2 垂直于弦的直径 垂径定理: 垂直于弦的直径平分弦,并且平分弦所对的两条弧. 垂径定理的推论: 平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
课后小结 教师与学生一起回顾本节课所学的主要内容,梳理并完善知识思维导图。
教学反思 垂径定理是中学数学中的一个很重要的定理,由于它涉及的条件结论比较多,学生容易搞混淆,本节课采取了讲练结合、动手操作的教学方法,课前布置所有同学制作一张圆形纸片,课上利用此纸片探索、体验圆是轴对称图形,并进一步利用圆的轴对称性探究垂径定理,环环相扣、逐层深入,激发学生的学习兴趣,收到了很好的教学效果.
同课章节目录
