24.1.4 圆周角 教案(表格式)2025-2026学年度人教版数学九年级上册
文档属性
| 名称 | 24.1.4 圆周角 教案(表格式)2025-2026学年度人教版数学九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-23 00:00:00 | ||
图片预览


文档简介
九年级上册教案
24.1 圆的有关性质
24.1.4 圆周角
教学内容 24.1.4 圆周角 课时 1
核心素养目标 1.理解圆周角的定义,会区分圆周角和圆心角;掌握圆周角定理及其两个推论,能在证明或计算中熟练的应用它们处理相关问题. 2.经历观察、类比、猜想、合作交流等数学活动,逐步会用运动变换的观点认识圆中的动态问题,渗透解决不确定问题的思路和方法. 3.掌握圆周角定理的推论,能够利用推论,解决圆、三角形、四边形相关的几何问题,培养几何直观能力,逻辑推理能力.
知识目标 1.掌握圆周角定理及其推论并能应用其进行简单的计算与证明. 2.掌握圆内接多边形的有关概念及性质.
教学重点 理解圆周角的概念;掌握圆周角与圆心角之间的关系定理.
教学难点 圆周角和圆心角关系定理的证明;掌握圆内接多边形的有关概念及性质.
教学准备 课件
教学过程 主要师生活动 设计意图
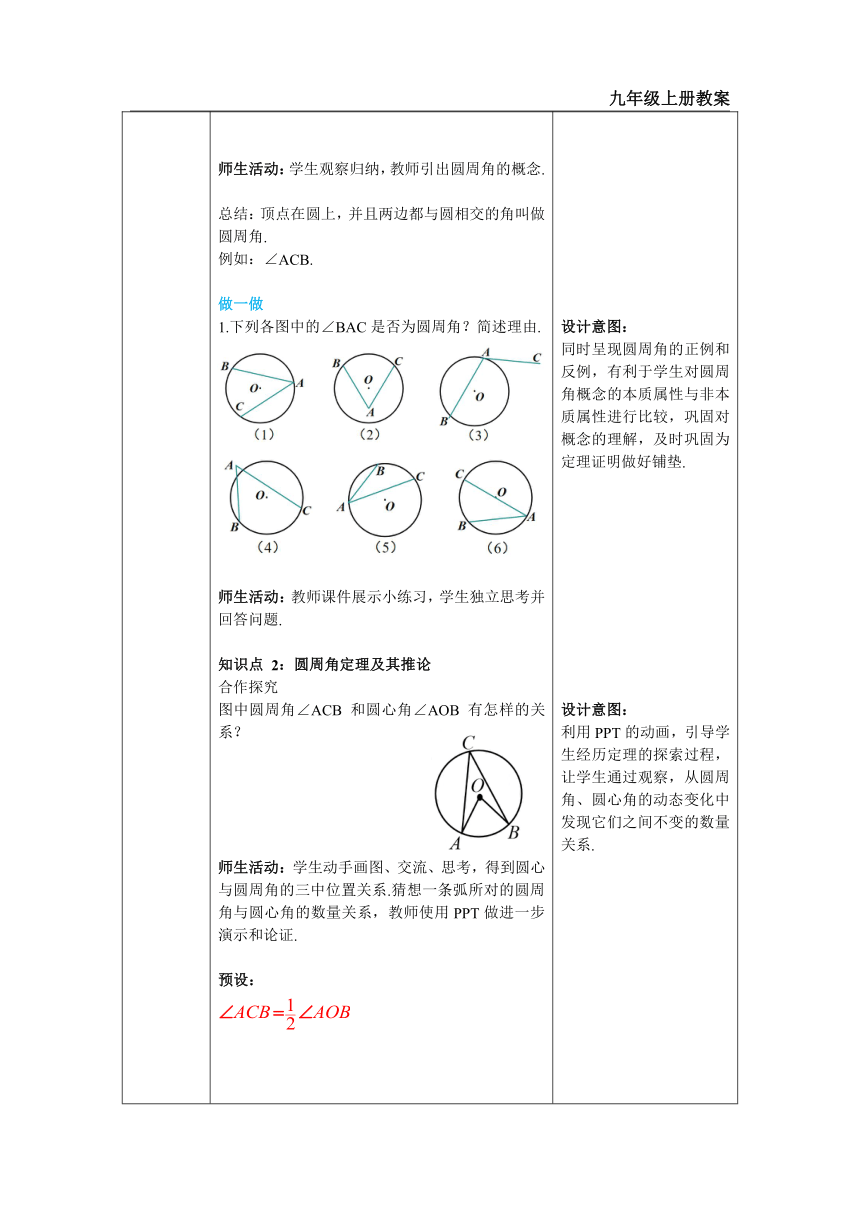
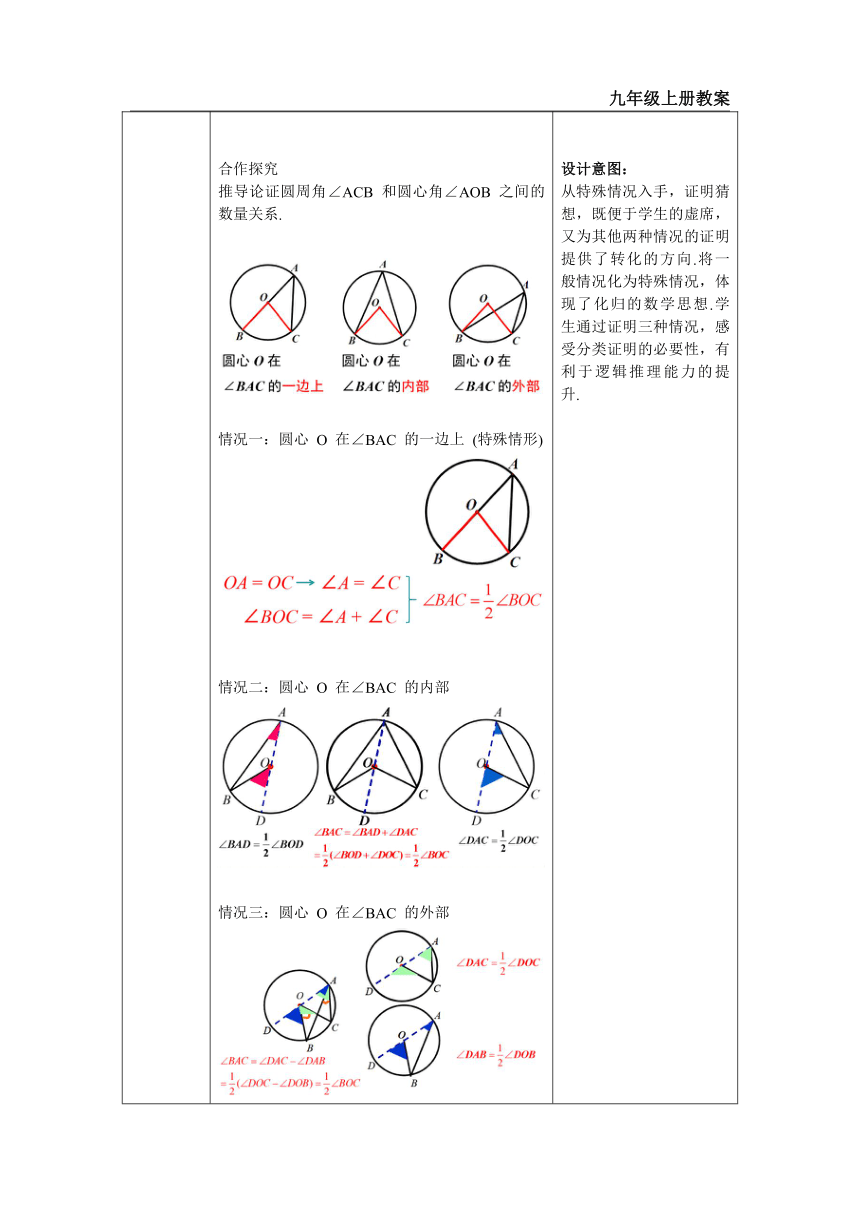
一、情境导入 二、探究新知 当堂练习,巩固所学 一、创设情境,导入新知 思考: 回想足球射门的过程,图中过球门 A、E 两点画圆,球员射中球门的难易程度与他所处的位置 B、C、D 有关(张开的角度大小)、仅从数学的角度考虑,球员应选择从哪一点的位置射门更有利? 为什么呢? 师生活动: 学生各抒己见,谈自己的看法. 二、小组合作,探究概念和性质 知识点一:圆周角的定义 如图,把圆心角∠AOB 的顶点 O 拉到圆上,得到∠ACB. 问题1:∠ACB 有什么特点?它与 ∠AOB 有何异同? 问题2:你能仿照圆心角的定义给 ∠ACB 取一个名字并下定义吗? 师生活动:学生观察归纳,教师引出圆周角的概念. 总结:顶点在圆上,并且两边都与圆相交的角叫做圆周角. 例如:∠ACB. 做一做 1.下列各图中的∠BAC是否为圆周角?简述理由. 师生活动:教师课件展示小练习,学生独立思考并回答问题. 知识点 2:圆周角定理及其推论 合作探究 图中圆周角∠ACB 和圆心角∠AOB 有怎样的关系? 师生活动:学生动手画图、交流、思考,得到圆心与圆周角的三中位置关系.猜想一条弧所对的圆周角与圆心角的数量关系,教师使用PPT做进一步演示和论证. 预设: 合作探究 推导论证圆周角∠ACB 和圆心角∠AOB 之间的数量关系. 情况一:圆心 O 在∠BAC 的一边上 (特殊情形) 情况二:圆心 O 在∠BAC 的内部 情况三:圆心 O 在∠BAC 的外部 师生活动:学生结合三种位置的图形,认识到:第(1)种属于特殊情况.研究数学问题一般从特殊情况开始,再考虑其他情况能否转化成特殊情况.如果学生有困难,教师可提示学生:将第(2)(3)种情况转化成第(1)种情况.根据学生的情况,师生共同完成第(2)种情况的证明.学生观察、猜想、证明圆周角定理的推论.教师可根据情况适当地提示学生. 师生共同总结: 圆周角定理: 一条弧所对的圆周角等于它所对的圆心角的一半. 想一想: 上节课我们学习了一个反映圆心角、圆心角所对的弧、圆心角所对的弦三个量之间关系的一个结论,这个结论是什么? 预设:在同圆(或等圆)中,如果圆心角、弧、弦有一组量相等,那么它们所对应的其余两个量都分别相等. 师提问:那么,圆周角与圆周角所对的弧、弦有什么关系吗? 圆周角与弧的关系 合作探究 问题1 如图,OB,OC 都是⊙O 的半径,点 A ,D 是圆上任意两点,连接 AB,AC,BD,CD. ∠BAC 与∠BDC 相等吗?请说明理由. 师生活动:学生根据圆周角的性质进行分析、讨论,教师引导总结. 圆周角推论1:同弧或等弧所对的圆周角相等. 圆周角与弦的关系 问题3 如图,线段 AB 是☉O 的直径,点 C 是☉O 上的任意一点 (除点 A、B 外),那么∠ACB 就是直径 AB 所对的圆周角. 想一想,∠ACB 会是怎样的角? 师生活动:学生画图、测量、比较、发现、猜想.再试一试,并在小组内交流,归纳总结,最后在全班交流. 本次探究活动,教师主要关注: (1)问题的提出是否引起学生的兴趣; (2)学生是否理解圆周角的定义; (3)学生是否清楚要研究的数学问题. 圆周角推论 2: 半圆(或直径)所对的圆周角是_直角__,90° 的圆周角所对的弦是直径. 典例精析 例1 如图,⊙O 的直径 AB 为 10 cm,弦 AC 为 6 cm.∠ACB 的平分线交⊙O 于点 D,求 BC,AD,BD 的长. 总结:解答圆周角有关问题时,若题中出现“直径”这个条件,则应考虑构造直角三角形来求解. 知识点 3:圆内接四边形 知识讲解 如果一个多边形的所有顶点都在同一个圆上,这个多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆. 合作探究 如图,四边形 ABCD 为⊙O 的内接四边形.探究 ∠A 与∠C,∠B 与∠D 之间的关系. 预设: ∠A +∠C = 180°, ∠B +∠D = 180°. 师提问:如何证明呢? 结论: 圆的内接四边形的对角互补. 三、当堂练习,巩固所学 1. (泗阳县期末)如图,AB 是 ⊙O 的直径,弦 CD 交AB 与点 E,∠ADC = 26°,求∠CAB 的度数. 2. (阜宁县期末)如图,AB 是⊙O 的直径, C、D 是 ⊙O 的两点,且 AD = DC ,∠DAC = 25°, 求∠BAC 的度数 ( ) A. 30° B. 35° C. 40° D. 50° 3. (武汉)如图,以 AB 为直径的⊙O 经过△ABC 的顶点 C,AE,BE 分别平分 ∠BAC 和 ∠ABC,AE 的延长线交⊙O 于点 D. 连接 BD. 判断△BDE 的形状,并证明你的结论. 设计意图: 从生活中的实例入手,让学生经历观察、分析,抽象出图形的共同属性,得出圆周角定义,理解圆周角概念的本质. 设计意图: 类比圆心角的定义,引出圆周角的概念,为后续学习奠定基础. 设计意图: 同时呈现圆周角的正例和反例,有利于学生对圆周角概念的本质属性与非本质属性进行比较,巩固对概念的理解,及时巩固为定理证明做好铺垫. 设计意图: 利用PPT的动画,引导学生经历定理的探索过程,让学生通过观察,从圆周角、圆心角的动态变化中发现它们之间不变的数量关系. 设计意图: 从特殊情况入手,证明猜想,既便于学生的虚席,又为其他两种情况的证明提供了转化的方向.将一般情况化为特殊情况,体现了化归的数学思想.学生通过证明三种情况,感受分类证明的必要性,有利于逻辑推理能力的提升. 设计意图:让学生在同一知识中变换角度思考问题,从不同的方位观察圆心角与圆周角,深入理解“等弧”“同弧”二字的含义,培养了学生思维的深度和广度. 设计意图:通过观察度量、推理来探索图形的性质,从而让学生学会分析问题和解决问题的方法.另外,尽可能地从教学语言的三种形态“文字语言、图形语言、符号语言”进行描述,以强化对数学知识的学习与理解,加强数学语言的运用与表达. 设计意图:加强学生对圆周角定理推论的理解和运用. 设计意图: 在教师的引导下,通过层层深入分析已知条件,结合圆周角和圆心角之间的关系,探究出圆内接四边形的性质,提高学生分析问题、解决问题的能力,同时培养学生将语言叙述转化为几何语言的能力,以及严谨的学习态度. 设计意图: 将本节所学内容与以前的知识紧密结合,使学生很好地进行知识的迁移,在练习中加深对本节知识的理解.
板书设计 24.1.4 圆周角 1.圆周角:顶点在圆上,两边都与圆相交的角. 2.圆周角定理: 一条弧所对的圆周角等于它所对的圆心角的一半. 推论: 同弧或等弧所对的圆周角相等. 半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径. 3.圆的内接四边形的对角互补.
课后小结 教师与学生一起回顾本节课所学的主要内容,梳理并完善知识思维导图。
教学反思 本节课采用问题情境——自主探究——拓展应用的课堂教学模式,以问题为主,配合多媒体辅助教学,引导学生进行有效思考.在教学过程中,通过问题串启发引导,学生自主探究,创设情境等多种教学方式,激发学生学习兴趣,调动课堂气氛,收到了很好的教学效果.
24.1 圆的有关性质
24.1.4 圆周角
教学内容 24.1.4 圆周角 课时 1
核心素养目标 1.理解圆周角的定义,会区分圆周角和圆心角;掌握圆周角定理及其两个推论,能在证明或计算中熟练的应用它们处理相关问题. 2.经历观察、类比、猜想、合作交流等数学活动,逐步会用运动变换的观点认识圆中的动态问题,渗透解决不确定问题的思路和方法. 3.掌握圆周角定理的推论,能够利用推论,解决圆、三角形、四边形相关的几何问题,培养几何直观能力,逻辑推理能力.
知识目标 1.掌握圆周角定理及其推论并能应用其进行简单的计算与证明. 2.掌握圆内接多边形的有关概念及性质.
教学重点 理解圆周角的概念;掌握圆周角与圆心角之间的关系定理.
教学难点 圆周角和圆心角关系定理的证明;掌握圆内接多边形的有关概念及性质.
教学准备 课件
教学过程 主要师生活动 设计意图
一、情境导入 二、探究新知 当堂练习,巩固所学 一、创设情境,导入新知 思考: 回想足球射门的过程,图中过球门 A、E 两点画圆,球员射中球门的难易程度与他所处的位置 B、C、D 有关(张开的角度大小)、仅从数学的角度考虑,球员应选择从哪一点的位置射门更有利? 为什么呢? 师生活动: 学生各抒己见,谈自己的看法. 二、小组合作,探究概念和性质 知识点一:圆周角的定义 如图,把圆心角∠AOB 的顶点 O 拉到圆上,得到∠ACB. 问题1:∠ACB 有什么特点?它与 ∠AOB 有何异同? 问题2:你能仿照圆心角的定义给 ∠ACB 取一个名字并下定义吗? 师生活动:学生观察归纳,教师引出圆周角的概念. 总结:顶点在圆上,并且两边都与圆相交的角叫做圆周角. 例如:∠ACB. 做一做 1.下列各图中的∠BAC是否为圆周角?简述理由. 师生活动:教师课件展示小练习,学生独立思考并回答问题. 知识点 2:圆周角定理及其推论 合作探究 图中圆周角∠ACB 和圆心角∠AOB 有怎样的关系? 师生活动:学生动手画图、交流、思考,得到圆心与圆周角的三中位置关系.猜想一条弧所对的圆周角与圆心角的数量关系,教师使用PPT做进一步演示和论证. 预设: 合作探究 推导论证圆周角∠ACB 和圆心角∠AOB 之间的数量关系. 情况一:圆心 O 在∠BAC 的一边上 (特殊情形) 情况二:圆心 O 在∠BAC 的内部 情况三:圆心 O 在∠BAC 的外部 师生活动:学生结合三种位置的图形,认识到:第(1)种属于特殊情况.研究数学问题一般从特殊情况开始,再考虑其他情况能否转化成特殊情况.如果学生有困难,教师可提示学生:将第(2)(3)种情况转化成第(1)种情况.根据学生的情况,师生共同完成第(2)种情况的证明.学生观察、猜想、证明圆周角定理的推论.教师可根据情况适当地提示学生. 师生共同总结: 圆周角定理: 一条弧所对的圆周角等于它所对的圆心角的一半. 想一想: 上节课我们学习了一个反映圆心角、圆心角所对的弧、圆心角所对的弦三个量之间关系的一个结论,这个结论是什么? 预设:在同圆(或等圆)中,如果圆心角、弧、弦有一组量相等,那么它们所对应的其余两个量都分别相等. 师提问:那么,圆周角与圆周角所对的弧、弦有什么关系吗? 圆周角与弧的关系 合作探究 问题1 如图,OB,OC 都是⊙O 的半径,点 A ,D 是圆上任意两点,连接 AB,AC,BD,CD. ∠BAC 与∠BDC 相等吗?请说明理由. 师生活动:学生根据圆周角的性质进行分析、讨论,教师引导总结. 圆周角推论1:同弧或等弧所对的圆周角相等. 圆周角与弦的关系 问题3 如图,线段 AB 是☉O 的直径,点 C 是☉O 上的任意一点 (除点 A、B 外),那么∠ACB 就是直径 AB 所对的圆周角. 想一想,∠ACB 会是怎样的角? 师生活动:学生画图、测量、比较、发现、猜想.再试一试,并在小组内交流,归纳总结,最后在全班交流. 本次探究活动,教师主要关注: (1)问题的提出是否引起学生的兴趣; (2)学生是否理解圆周角的定义; (3)学生是否清楚要研究的数学问题. 圆周角推论 2: 半圆(或直径)所对的圆周角是_直角__,90° 的圆周角所对的弦是直径. 典例精析 例1 如图,⊙O 的直径 AB 为 10 cm,弦 AC 为 6 cm.∠ACB 的平分线交⊙O 于点 D,求 BC,AD,BD 的长. 总结:解答圆周角有关问题时,若题中出现“直径”这个条件,则应考虑构造直角三角形来求解. 知识点 3:圆内接四边形 知识讲解 如果一个多边形的所有顶点都在同一个圆上,这个多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆. 合作探究 如图,四边形 ABCD 为⊙O 的内接四边形.探究 ∠A 与∠C,∠B 与∠D 之间的关系. 预设: ∠A +∠C = 180°, ∠B +∠D = 180°. 师提问:如何证明呢? 结论: 圆的内接四边形的对角互补. 三、当堂练习,巩固所学 1. (泗阳县期末)如图,AB 是 ⊙O 的直径,弦 CD 交AB 与点 E,∠ADC = 26°,求∠CAB 的度数. 2. (阜宁县期末)如图,AB 是⊙O 的直径, C、D 是 ⊙O 的两点,且 AD = DC ,∠DAC = 25°, 求∠BAC 的度数 ( ) A. 30° B. 35° C. 40° D. 50° 3. (武汉)如图,以 AB 为直径的⊙O 经过△ABC 的顶点 C,AE,BE 分别平分 ∠BAC 和 ∠ABC,AE 的延长线交⊙O 于点 D. 连接 BD. 判断△BDE 的形状,并证明你的结论. 设计意图: 从生活中的实例入手,让学生经历观察、分析,抽象出图形的共同属性,得出圆周角定义,理解圆周角概念的本质. 设计意图: 类比圆心角的定义,引出圆周角的概念,为后续学习奠定基础. 设计意图: 同时呈现圆周角的正例和反例,有利于学生对圆周角概念的本质属性与非本质属性进行比较,巩固对概念的理解,及时巩固为定理证明做好铺垫. 设计意图: 利用PPT的动画,引导学生经历定理的探索过程,让学生通过观察,从圆周角、圆心角的动态变化中发现它们之间不变的数量关系. 设计意图: 从特殊情况入手,证明猜想,既便于学生的虚席,又为其他两种情况的证明提供了转化的方向.将一般情况化为特殊情况,体现了化归的数学思想.学生通过证明三种情况,感受分类证明的必要性,有利于逻辑推理能力的提升. 设计意图:让学生在同一知识中变换角度思考问题,从不同的方位观察圆心角与圆周角,深入理解“等弧”“同弧”二字的含义,培养了学生思维的深度和广度. 设计意图:通过观察度量、推理来探索图形的性质,从而让学生学会分析问题和解决问题的方法.另外,尽可能地从教学语言的三种形态“文字语言、图形语言、符号语言”进行描述,以强化对数学知识的学习与理解,加强数学语言的运用与表达. 设计意图:加强学生对圆周角定理推论的理解和运用. 设计意图: 在教师的引导下,通过层层深入分析已知条件,结合圆周角和圆心角之间的关系,探究出圆内接四边形的性质,提高学生分析问题、解决问题的能力,同时培养学生将语言叙述转化为几何语言的能力,以及严谨的学习态度. 设计意图: 将本节所学内容与以前的知识紧密结合,使学生很好地进行知识的迁移,在练习中加深对本节知识的理解.
板书设计 24.1.4 圆周角 1.圆周角:顶点在圆上,两边都与圆相交的角. 2.圆周角定理: 一条弧所对的圆周角等于它所对的圆心角的一半. 推论: 同弧或等弧所对的圆周角相等. 半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径. 3.圆的内接四边形的对角互补.
课后小结 教师与学生一起回顾本节课所学的主要内容,梳理并完善知识思维导图。
教学反思 本节课采用问题情境——自主探究——拓展应用的课堂教学模式,以问题为主,配合多媒体辅助教学,引导学生进行有效思考.在教学过程中,通过问题串启发引导,学生自主探究,创设情境等多种教学方式,激发学生学习兴趣,调动课堂气氛,收到了很好的教学效果.
同课章节目录
