24.3 正多边形和圆 教案(表格式)2025-2026学年度人教版数学九年级上册
文档属性
| 名称 | 24.3 正多边形和圆 教案(表格式)2025-2026学年度人教版数学九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-23 09:42:08 | ||
图片预览

文档简介
九年级上册教案
24.3 正多边形和圆
教学内容 24.3 正多边形和圆 课时 1
核心素养目标 1.掌握正多边形的概念与正多边形和圆的关系,并能进行有关计算; 2.正多边形的半径、边心距及边长的计算问题转化为解直角三角形的问题,学会类比转化的思想; 3.培养学生的观察力和几何思维能力,通过研究正多边形和圆的特点,学生需要观察并发现其中的规律并进行推理,有利于培养学生的逻辑思维和空间想象能力.
知识目标 1.了解正多边形和圆的有关概念. 2.理解并掌握正多边形半径和边长、边心距、中心角之间的关系. 3.会应用正多边形和圆的有关知识画正多边形.
教学重点 理解并掌握正多边形半径和边长、边心距、中心角之间的关系
教学难点 理解并掌握正多边形半径和边长、边心距、中心角之间的关系
教学准备 课件
教学过程 主要师生活动 设计意图
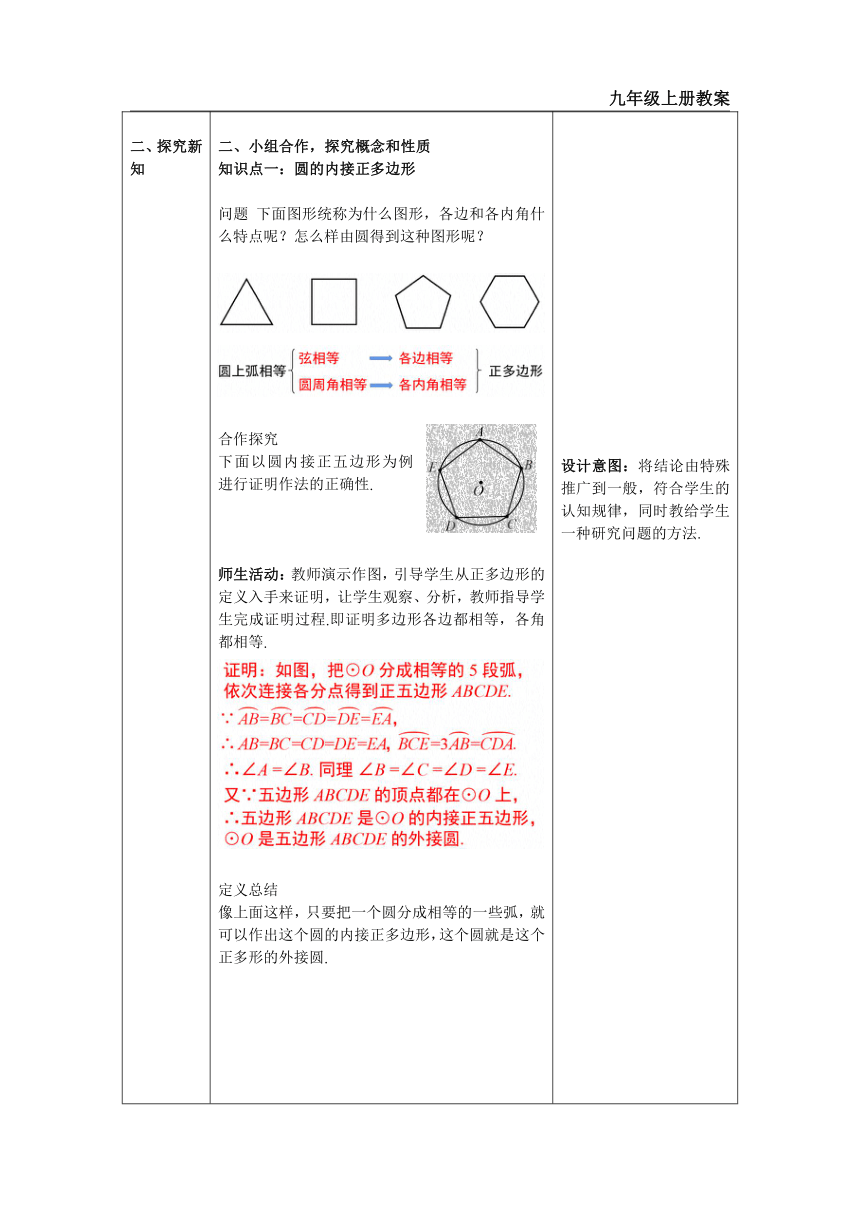
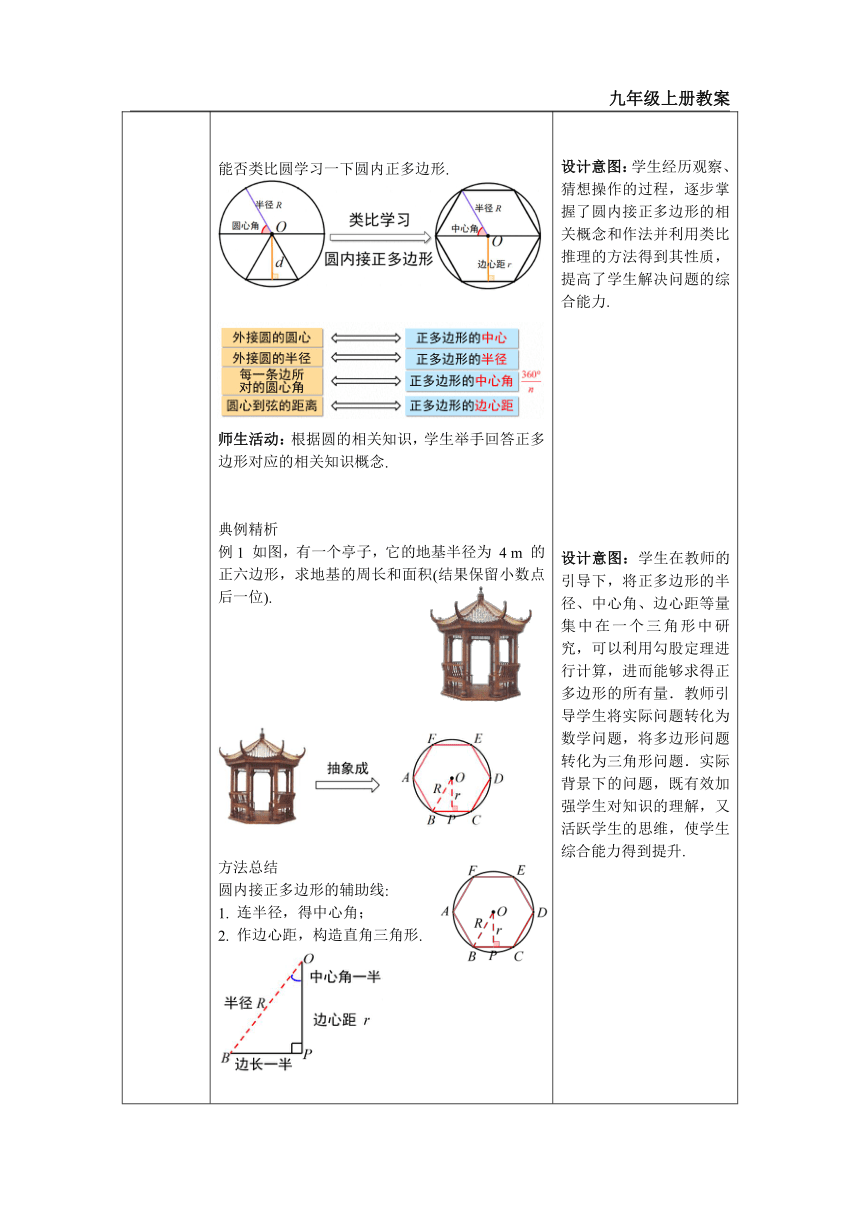
一、情境导入 二、探究新知 当堂练习,巩固所学 一、创设情境,导入新知 下图的这些图案,都是我们在日常生活中经常看到的. 你能从这些图案中找出基本的几何图形吗 师生活动:教师提出问题,引导学生回答,师生共同回顾、交流,适时做好总结. 预设: 二、小组合作,探究概念和性质 知识点一:圆的内接正多边形 问题 下面图形统称为什么图形,各边和各内角什么特点呢?怎么样由圆得到这种图形呢? 合作探究 下面以圆内接正五边形为例进行证明作法的正确性. 师生活动:教师演示作图,引导学生从正多边形的定义入手来证明,让学生观察、分析,教师指导学生完成证明过程.即证明多边形各边都相等,各角都相等. 定义总结 像上面这样,只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多形的外接圆. 能否类比圆学习一下圆内正多边形. 师生活动:根据圆的相关知识,学生举手回答正多边形对应的相关知识概念. 典例精析 例1 如图,有一个亭子,它的地基半径为 4 m 的正六边形,求地基的周长和面积(结果保留小数点后一位). 方法总结 圆内接正多边形的辅助线: 1. 连半径,得中心角; 2. 作边心距,构造直角三角形. 链接中考 (雅安)如图,已知 ⊙O 的周长等于 6π,则该圆内接正六边形 ABCDEF 的边心距 OG 为 ( ) 2. (青岛)如图,正六边形ABCDEF 内接于 ⊙O ,点 M 在 上,则 ∠CME 的度数为 ( )
A.30° B.36°
C.45° D.60° 师生活动: 学生自主动手解决,老师进行订正. 知识点 2:正多边形作图 合作探究 请探索其他等分圆周的方法作任意的正 n 边形. 量角器等分圆周 正三角形为例. 动手实践 你能用以上方法画出正四边形、正五边形、正六边形吗? 旋转作图等分圆周 正三角形为例. 总结:正多边形作图多样,要注意每种方法作图限制及原理. 三、当堂练习,巩固所学 1. 在半径 R 的圆上依次截取等于 R 的弦,顺次连接各分点得到的多边形是 ( ) A.正三角 B.正方形 C.正五边形 D.正六边形 2. 已知正六边形 ABCDEF 内接于⊙O ,正六边形的周长是 24 ,则⊙O 的半径长是 ( ) 3. 如图,已知点 O 是正六边形 ABCDEF 的对称中心,G,H 分别是 AF,BC 上的点,且 AG = BH. (1) 求∠FAB 的度数; (2) 求证:OG = OH. 拓广探索:如图,M,N 分别是☉O 内接正多边形的边AB,BC 上的点,且 BM = CN. 图①中∠MON = °, 图②中∠MON = °, 图③中∠MON = °; (2) 试探究∠MON 的度数与正 n 边形的边数 n 的关系. 设计意图: 创设情境,激发学生学习的兴趣和探究欲望,为本节课的探究做好铺垫. 设计意图:将结论由特殊推广到一般,符合学生的认知规律,同时教给学生一种研究问题的方法. 设计意图:学生经历观察、 猜想操作的过程,逐步掌握了圆内接正多边形的相关概念和作法并利用类比推理的方法得到其性质,提高了学生解决问题的综合能力. 设计意图:学生在教师的引导下,将正多边形的半径、中心角、边心距等量集中在一个三角形中研究,可以利用勾股定理进行计算,进而能够求得正多边形的所有量.教师引导学生将实际问题转化为数学问题,将多边形问题转化为三角形问题.实际背景下的问题,既有效加强学生对知识的理解,又活跃学生的思维,使学生综合能力得到提升. 设计意图: 本环节一是检验学生学习状况,二是让学生产生一种利用新知解决问题的成就感,提升学生学习积极性. 设计意图:通过探索,得出等分圆弧的方法,利用等分圆弧的方法画圆内接正三角形、正方形、正五边形、正六边形、正八边形。 设计意图:及时练习巩固,体现学以致用的观念,消除学生学无所用的思想顾虑.
板书设计 正多边形和圆
课后小结 教师与学生一起回顾本节课所学的主要内容,梳理并完善知识思维导图。
教学反思 探索正多边形与圆的关系,理解正多边形的中心,半径、中心角、边心距等有关概念,理解利用尺规等分圆周的方法,进而作圆内接正多边形。在教学中应鼓励学生积极思考,归纳总结,允许学生回答的不完整,甚至有错误的见解,培养学生乐于分享、发言的习惯,提高学生学习数学的兴趣。通过观察、分析、动手操作、画图等过程,增强审美能力和对图形的欣赏能力.
24.3 正多边形和圆
教学内容 24.3 正多边形和圆 课时 1
核心素养目标 1.掌握正多边形的概念与正多边形和圆的关系,并能进行有关计算; 2.正多边形的半径、边心距及边长的计算问题转化为解直角三角形的问题,学会类比转化的思想; 3.培养学生的观察力和几何思维能力,通过研究正多边形和圆的特点,学生需要观察并发现其中的规律并进行推理,有利于培养学生的逻辑思维和空间想象能力.
知识目标 1.了解正多边形和圆的有关概念. 2.理解并掌握正多边形半径和边长、边心距、中心角之间的关系. 3.会应用正多边形和圆的有关知识画正多边形.
教学重点 理解并掌握正多边形半径和边长、边心距、中心角之间的关系
教学难点 理解并掌握正多边形半径和边长、边心距、中心角之间的关系
教学准备 课件
教学过程 主要师生活动 设计意图
一、情境导入 二、探究新知 当堂练习,巩固所学 一、创设情境,导入新知 下图的这些图案,都是我们在日常生活中经常看到的. 你能从这些图案中找出基本的几何图形吗 师生活动:教师提出问题,引导学生回答,师生共同回顾、交流,适时做好总结. 预设: 二、小组合作,探究概念和性质 知识点一:圆的内接正多边形 问题 下面图形统称为什么图形,各边和各内角什么特点呢?怎么样由圆得到这种图形呢? 合作探究 下面以圆内接正五边形为例进行证明作法的正确性. 师生活动:教师演示作图,引导学生从正多边形的定义入手来证明,让学生观察、分析,教师指导学生完成证明过程.即证明多边形各边都相等,各角都相等. 定义总结 像上面这样,只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多形的外接圆. 能否类比圆学习一下圆内正多边形. 师生活动:根据圆的相关知识,学生举手回答正多边形对应的相关知识概念. 典例精析 例1 如图,有一个亭子,它的地基半径为 4 m 的正六边形,求地基的周长和面积(结果保留小数点后一位). 方法总结 圆内接正多边形的辅助线: 1. 连半径,得中心角; 2. 作边心距,构造直角三角形. 链接中考 (雅安)如图,已知 ⊙O 的周长等于 6π,则该圆内接正六边形 ABCDEF 的边心距 OG 为 ( ) 2. (青岛)如图,正六边形ABCDEF 内接于 ⊙O ,点 M 在 上,则 ∠CME 的度数为 ( )
A.30° B.36°
C.45° D.60° 师生活动: 学生自主动手解决,老师进行订正. 知识点 2:正多边形作图 合作探究 请探索其他等分圆周的方法作任意的正 n 边形. 量角器等分圆周 正三角形为例. 动手实践 你能用以上方法画出正四边形、正五边形、正六边形吗? 旋转作图等分圆周 正三角形为例. 总结:正多边形作图多样,要注意每种方法作图限制及原理. 三、当堂练习,巩固所学 1. 在半径 R 的圆上依次截取等于 R 的弦,顺次连接各分点得到的多边形是 ( ) A.正三角 B.正方形 C.正五边形 D.正六边形 2. 已知正六边形 ABCDEF 内接于⊙O ,正六边形的周长是 24 ,则⊙O 的半径长是 ( ) 3. 如图,已知点 O 是正六边形 ABCDEF 的对称中心,G,H 分别是 AF,BC 上的点,且 AG = BH. (1) 求∠FAB 的度数; (2) 求证:OG = OH. 拓广探索:如图,M,N 分别是☉O 内接正多边形的边AB,BC 上的点,且 BM = CN. 图①中∠MON = °, 图②中∠MON = °, 图③中∠MON = °; (2) 试探究∠MON 的度数与正 n 边形的边数 n 的关系. 设计意图: 创设情境,激发学生学习的兴趣和探究欲望,为本节课的探究做好铺垫. 设计意图:将结论由特殊推广到一般,符合学生的认知规律,同时教给学生一种研究问题的方法. 设计意图:学生经历观察、 猜想操作的过程,逐步掌握了圆内接正多边形的相关概念和作法并利用类比推理的方法得到其性质,提高了学生解决问题的综合能力. 设计意图:学生在教师的引导下,将正多边形的半径、中心角、边心距等量集中在一个三角形中研究,可以利用勾股定理进行计算,进而能够求得正多边形的所有量.教师引导学生将实际问题转化为数学问题,将多边形问题转化为三角形问题.实际背景下的问题,既有效加强学生对知识的理解,又活跃学生的思维,使学生综合能力得到提升. 设计意图: 本环节一是检验学生学习状况,二是让学生产生一种利用新知解决问题的成就感,提升学生学习积极性. 设计意图:通过探索,得出等分圆弧的方法,利用等分圆弧的方法画圆内接正三角形、正方形、正五边形、正六边形、正八边形。 设计意图:及时练习巩固,体现学以致用的观念,消除学生学无所用的思想顾虑.
板书设计 正多边形和圆
课后小结 教师与学生一起回顾本节课所学的主要内容,梳理并完善知识思维导图。
教学反思 探索正多边形与圆的关系,理解正多边形的中心,半径、中心角、边心距等有关概念,理解利用尺规等分圆周的方法,进而作圆内接正多边形。在教学中应鼓励学生积极思考,归纳总结,允许学生回答的不完整,甚至有错误的见解,培养学生乐于分享、发言的习惯,提高学生学习数学的兴趣。通过观察、分析、动手操作、画图等过程,增强审美能力和对图形的欣赏能力.
同课章节目录
