24.4 第2课时 圆锥的侧面积和全面积 教案(表格式)2025-2026学年度人教版数学九年级上册
文档属性
| 名称 | 24.4 第2课时 圆锥的侧面积和全面积 教案(表格式)2025-2026学年度人教版数学九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-23 10:27:22 | ||
图片预览

文档简介
九年级上册教案
24.4 弧长和扇形面积
第2课时 圆锥的侧面积和全面积
教学内容 第2课时 圆锥的侧面积和全面积 课时 1
核心素养目标 1.掌握弧长和扇形面积的计算公式;并能灵活应用,解决实际问题; 2.利用圆的周长及面积公式,推导弧长和扇形面积的计算公式,培养学生由“特 殊到一般”的数学思想,发展学生合情推理的能力; 3.通过学生对图形观察、对比、归纳,激发学生的求知欲,并在运用数学知识解答问题的活动中获取成功的体验,建立学习的自信心.
知识目标 1.经历圆锥侧面积的探索过程. 2.会求圆锥的侧面积和全面积,并能解决一些简单的实际问题.
教学重点 会求圆锥的侧面积和全面积,并能解决一些简单的实际问题..
教学难点 会求圆锥的侧面积和全面积,并能解决一些简单的实际问题.
教学准备 课件
教学过程 主要师生活动 设计意图
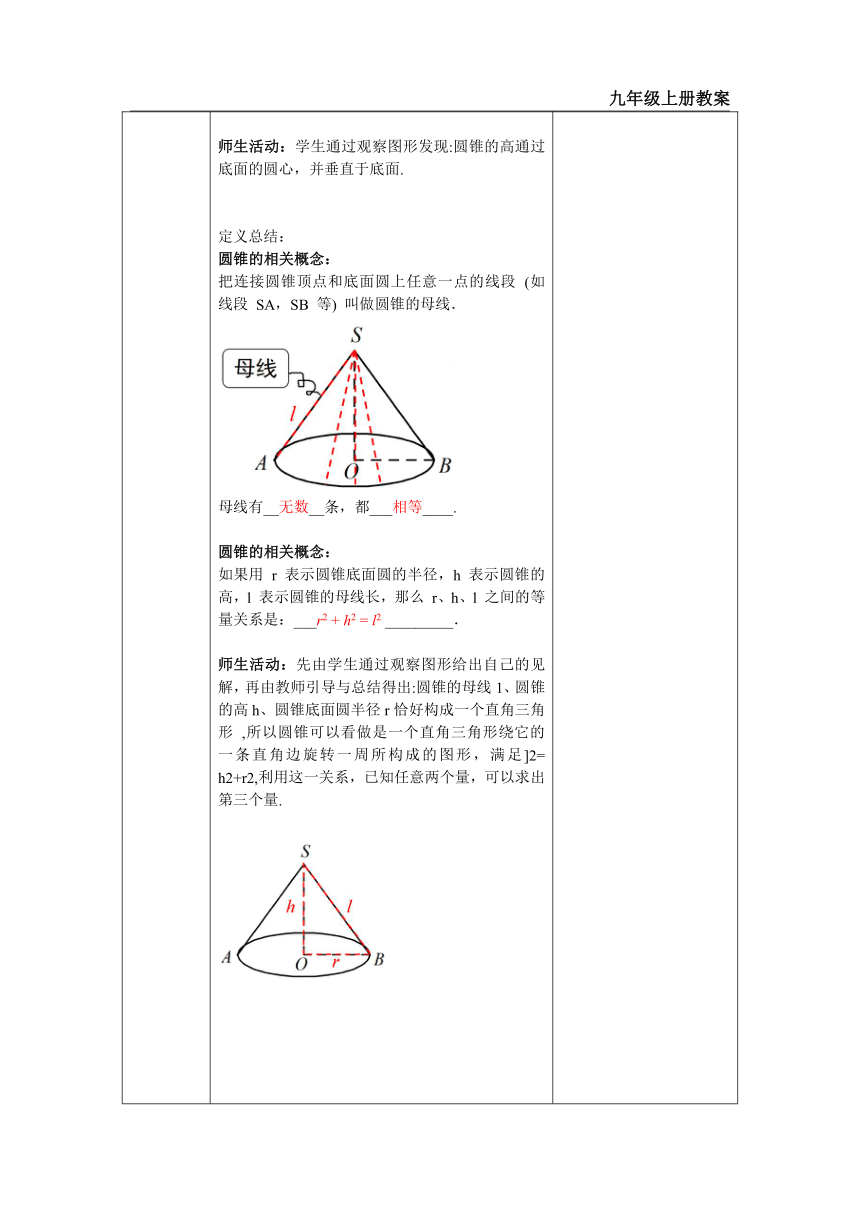
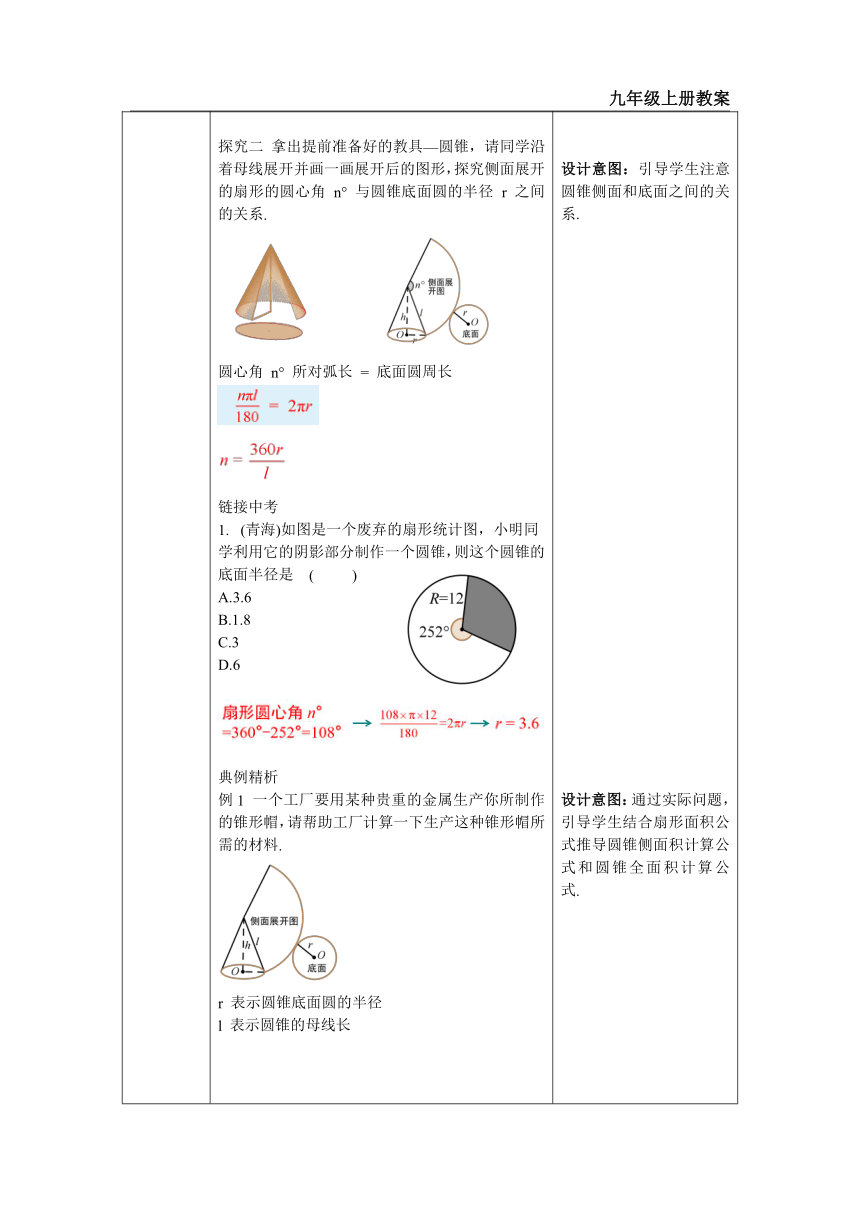
一、情境导入 二、探究新知 当堂练习,巩固所学 一、创设情境,导入新知 观察下面图片,你能从中看出什么图形吗? 预设:圆锥 师生活动:让学生自主回答. (学生积极踊跃发言,问答提出的问题.) 二、小组合作,探究概念和性质 知识点一:圆锥及其相关概念 探究一 观察右图圆锥的形成轨迹,说说它有哪些特征. 师生活动:学生通过观察图形发现:圆锥的高通过底面的圆心,并垂直于底面. 定义总结: 圆锥的相关概念: 把连接圆锥顶点和底面圆上任意一点的线段 (如线段 SA,SB 等) 叫做圆锥的母线. 母线有__无数__条,都___相等____. 圆锥的相关概念: 如果用 r 表示圆锥底面圆的半径,h 表示圆锥的高,l 表示圆锥的母线长,那么 r、h、l 之间的等量关系是:___r2 + h2 = l2 _________. 师生活动:先由学生通过观察图形给出自己的见解,再由教师引导与总结得出:圆锥的母线1、圆锥的高h、圆锥底面圆半径r恰好构成一个直角三角形 ,所以圆锥可以看做是一个直角三角形绕它的一条直角边旋转一周所构成的图形,满足]2= h2+r2,利用这一关系,已知任意两个量,可以求出第三个量. 探究二 拿出提前准备好的教具—圆锥,请同学沿着母线展开并画一画展开后的图形,探究侧面展开的扇形的圆心角 n° 与圆锥底面圆的半径 r 之间的关系. 圆心角 n° 所对弧长 = 底面圆周长 链接中考 (青海)如图是一个废弃的扇形统计图,小明同学利用它的阴影部分制作一个圆锥,则这个圆锥的底面半径是 ( )
A.3.6 B.1.8
C.3 D.6 典例精析 例1 一个工厂要用某种贵重的金属生产你所制作的锥形帽,请帮助工厂计算一下生产这种锥形帽所需的材料. r 表示圆锥底面圆的半径 l 表示圆锥的母线长 所需的材料:计算圆锥全面积 S全 = S侧+S底= πrl+ πr2 = πrl S底 = πr2 圆锥侧面积:S侧 = πrl. 圆锥全面积: S全 = S侧 + S底 = πrl+ πr2 = πr(l+r). 例2 蒙古包可以近似地看作由圆锥和圆柱组成,如果想用毛毡搭建 20 个底面积为 12 m2,高为 3.2 m,外围高为 1.8 m 的蒙古包,至少需要多少平方米的毛毡 ( π 取3.142,结果取整数 ) ? 师生活动: 学生自主思考,独立解题,老师给予订正. 解:如图是蒙古包的示意图.根据题意, 下面圆柱的底面积为 12 m2, 高为 h2 = 1.8 m; 上面圆锥的高为 h1 = 3.2-1.8 = 1.4(m). 三、当堂练习,巩固所学 1. 圆锥的底面半径为 3 cm,母线长为 6 cm,则这个圆锥侧面展开图扇形的圆心角是_____. 2. 已知圆锥的底面圆半径为 3 cm,高为 4 cm,则它的侧面积是 ,全面积是 . 3.如图所示,有一个圆锥形的粮堆,其轴截面是边长为 6 m 的等边三角形,在圆锥的母线 AC 的中点 P 处有一只老鼠正在偷吃粮食,此时小猫正在点 B 处,它要沿圆锥侧面到达点 P 处捕捉老鼠.求小猫所经过的最短路程. 4. (1) 在半径为 10 的圆形铁片中,要裁剪出一个直角扇形,求能裁剪出的最大的直角扇形的面积; (2) 若用这个最大的直角扇形恰好围成一个圆锥,求这个圆锥的底面圆的半径; (3) 能否从最大的余料③中剪出一个圆做该圆锥的底面?请说明理由. 设计意图: 创设情境,激发学生学习的兴趣和探究欲望,为本节课的探究做好铺垫. 设计意图:通过观察圆锥形成的动图过程,体会其特性. 设计意图:引导学生注意圆锥侧面和底面之间的关系. 设计意图:通过实际问题, 引导学生结合扇形面积公式推导圆锥侧面积计算公式和圆锥全面积计算公式. 设计意图:通过实际应用,不仅能很好地吸引学生注意力,还能让学生切身体会到生活中处处都时数学,感受数学美,培养学生用数学眼光观察显示世界的意识,学生感受从具体的蒙古包抽象出几何图形的过程,培养学生的几何直观. 设计意图:及时练习巩固,体现学以致用的观念,消除学生学无所用的思想顾虑.
板书设计 第2课时 圆锥的侧面积和全面积 圆锥侧面积:S侧 = πrl. 圆锥全面积: S全 = S侧 + S底= πrl+ πr2 = πr(l+r).
课后小结 教师与学生一起回顾本节课所学的主要内容,梳理并完善知识思维导图。
教学反思 经历学生对圆锥展开图的认识,与扇形面积公式的联系推导得出圆锥侧面积的计算公式及圆锥全面积的计算公式,并会应用公式解决问题。在教学中应鼓励学生积极思考,归纳总结,允许学生回答的不完整,甚至有错误的见解,培养学生乐于分享、发言的习惯,提高学生学习数学的兴趣。
24.4 弧长和扇形面积
第2课时 圆锥的侧面积和全面积
教学内容 第2课时 圆锥的侧面积和全面积 课时 1
核心素养目标 1.掌握弧长和扇形面积的计算公式;并能灵活应用,解决实际问题; 2.利用圆的周长及面积公式,推导弧长和扇形面积的计算公式,培养学生由“特 殊到一般”的数学思想,发展学生合情推理的能力; 3.通过学生对图形观察、对比、归纳,激发学生的求知欲,并在运用数学知识解答问题的活动中获取成功的体验,建立学习的自信心.
知识目标 1.经历圆锥侧面积的探索过程. 2.会求圆锥的侧面积和全面积,并能解决一些简单的实际问题.
教学重点 会求圆锥的侧面积和全面积,并能解决一些简单的实际问题..
教学难点 会求圆锥的侧面积和全面积,并能解决一些简单的实际问题.
教学准备 课件
教学过程 主要师生活动 设计意图
一、情境导入 二、探究新知 当堂练习,巩固所学 一、创设情境,导入新知 观察下面图片,你能从中看出什么图形吗? 预设:圆锥 师生活动:让学生自主回答. (学生积极踊跃发言,问答提出的问题.) 二、小组合作,探究概念和性质 知识点一:圆锥及其相关概念 探究一 观察右图圆锥的形成轨迹,说说它有哪些特征. 师生活动:学生通过观察图形发现:圆锥的高通过底面的圆心,并垂直于底面. 定义总结: 圆锥的相关概念: 把连接圆锥顶点和底面圆上任意一点的线段 (如线段 SA,SB 等) 叫做圆锥的母线. 母线有__无数__条,都___相等____. 圆锥的相关概念: 如果用 r 表示圆锥底面圆的半径,h 表示圆锥的高,l 表示圆锥的母线长,那么 r、h、l 之间的等量关系是:___r2 + h2 = l2 _________. 师生活动:先由学生通过观察图形给出自己的见解,再由教师引导与总结得出:圆锥的母线1、圆锥的高h、圆锥底面圆半径r恰好构成一个直角三角形 ,所以圆锥可以看做是一个直角三角形绕它的一条直角边旋转一周所构成的图形,满足]2= h2+r2,利用这一关系,已知任意两个量,可以求出第三个量. 探究二 拿出提前准备好的教具—圆锥,请同学沿着母线展开并画一画展开后的图形,探究侧面展开的扇形的圆心角 n° 与圆锥底面圆的半径 r 之间的关系. 圆心角 n° 所对弧长 = 底面圆周长 链接中考 (青海)如图是一个废弃的扇形统计图,小明同学利用它的阴影部分制作一个圆锥,则这个圆锥的底面半径是 ( )
A.3.6 B.1.8
C.3 D.6 典例精析 例1 一个工厂要用某种贵重的金属生产你所制作的锥形帽,请帮助工厂计算一下生产这种锥形帽所需的材料. r 表示圆锥底面圆的半径 l 表示圆锥的母线长 所需的材料:计算圆锥全面积 S全 = S侧+S底= πrl+ πr2 = πrl S底 = πr2 圆锥侧面积:S侧 = πrl. 圆锥全面积: S全 = S侧 + S底 = πrl+ πr2 = πr(l+r). 例2 蒙古包可以近似地看作由圆锥和圆柱组成,如果想用毛毡搭建 20 个底面积为 12 m2,高为 3.2 m,外围高为 1.8 m 的蒙古包,至少需要多少平方米的毛毡 ( π 取3.142,结果取整数 ) ? 师生活动: 学生自主思考,独立解题,老师给予订正. 解:如图是蒙古包的示意图.根据题意, 下面圆柱的底面积为 12 m2, 高为 h2 = 1.8 m; 上面圆锥的高为 h1 = 3.2-1.8 = 1.4(m). 三、当堂练习,巩固所学 1. 圆锥的底面半径为 3 cm,母线长为 6 cm,则这个圆锥侧面展开图扇形的圆心角是_____. 2. 已知圆锥的底面圆半径为 3 cm,高为 4 cm,则它的侧面积是 ,全面积是 . 3.如图所示,有一个圆锥形的粮堆,其轴截面是边长为 6 m 的等边三角形,在圆锥的母线 AC 的中点 P 处有一只老鼠正在偷吃粮食,此时小猫正在点 B 处,它要沿圆锥侧面到达点 P 处捕捉老鼠.求小猫所经过的最短路程. 4. (1) 在半径为 10 的圆形铁片中,要裁剪出一个直角扇形,求能裁剪出的最大的直角扇形的面积; (2) 若用这个最大的直角扇形恰好围成一个圆锥,求这个圆锥的底面圆的半径; (3) 能否从最大的余料③中剪出一个圆做该圆锥的底面?请说明理由. 设计意图: 创设情境,激发学生学习的兴趣和探究欲望,为本节课的探究做好铺垫. 设计意图:通过观察圆锥形成的动图过程,体会其特性. 设计意图:引导学生注意圆锥侧面和底面之间的关系. 设计意图:通过实际问题, 引导学生结合扇形面积公式推导圆锥侧面积计算公式和圆锥全面积计算公式. 设计意图:通过实际应用,不仅能很好地吸引学生注意力,还能让学生切身体会到生活中处处都时数学,感受数学美,培养学生用数学眼光观察显示世界的意识,学生感受从具体的蒙古包抽象出几何图形的过程,培养学生的几何直观. 设计意图:及时练习巩固,体现学以致用的观念,消除学生学无所用的思想顾虑.
板书设计 第2课时 圆锥的侧面积和全面积 圆锥侧面积:S侧 = πrl. 圆锥全面积: S全 = S侧 + S底= πrl+ πr2 = πr(l+r).
课后小结 教师与学生一起回顾本节课所学的主要内容,梳理并完善知识思维导图。
教学反思 经历学生对圆锥展开图的认识,与扇形面积公式的联系推导得出圆锥侧面积的计算公式及圆锥全面积的计算公式,并会应用公式解决问题。在教学中应鼓励学生积极思考,归纳总结,允许学生回答的不完整,甚至有错误的见解,培养学生乐于分享、发言的习惯,提高学生学习数学的兴趣。
同课章节目录
