4.4一次函数的应用同步练习(含解析)北师大版数学八年级上册
文档属性
| 名称 | 4.4一次函数的应用同步练习(含解析)北师大版数学八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-24 20:33:59 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
4.4一次函数的应用
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.一次函数与轴相交于点,则关于的方程的解为( )
A. B. C. D.无法求解
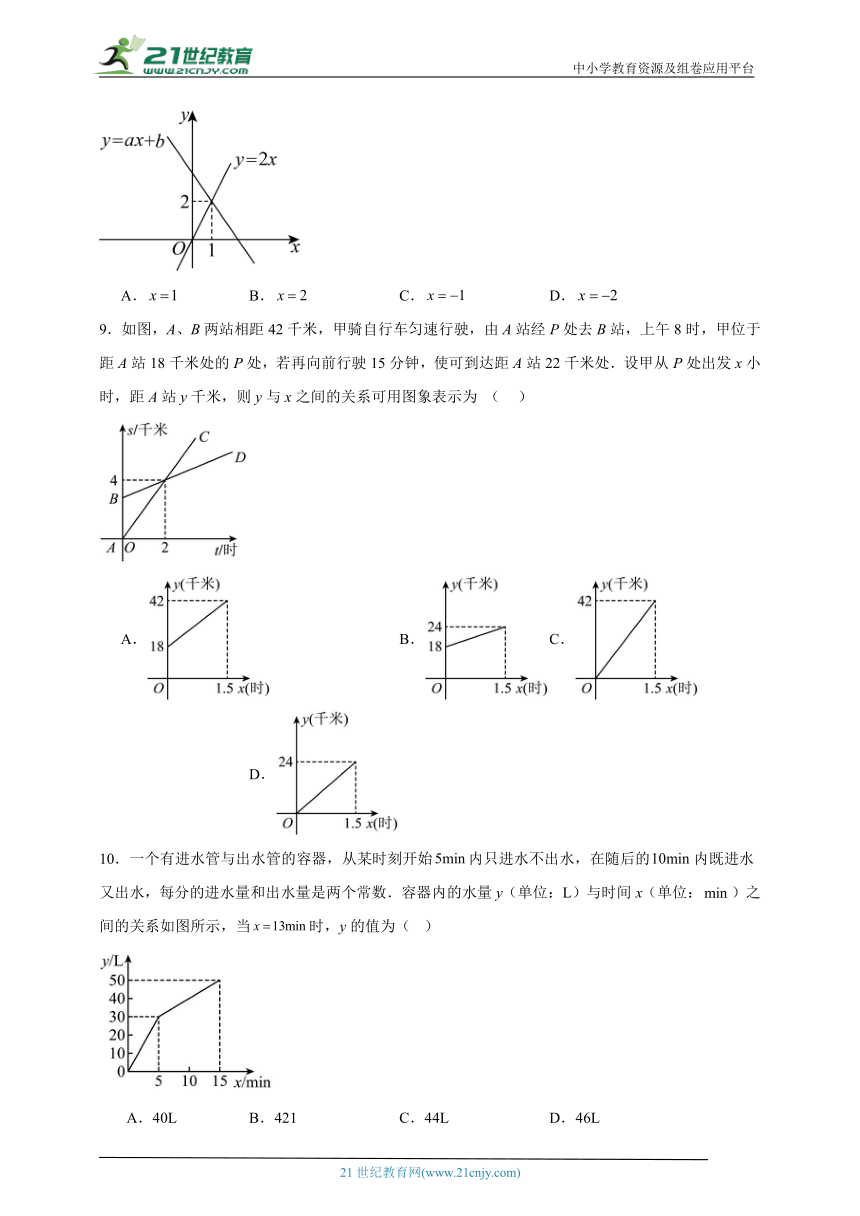
2.甲、乙两位同学放学后走路回家,他们走过的路程(单位:)与所用的时间(单位:)之间的关系如图所示.根据图中信息,下列说法正确的是( )
A.乙走的路程比甲远
B.甲的平均速度为
C.前,甲的速度比乙快
D.经过,甲、乙都走了
3.在一条沿山而建的游览路线上依次有三处观景台,小方从处徒步前往处,同时小圆从处骑车前往处,到达处后休息1分钟,然后立即折返(折返时间忽略不计)按原路原速前往处,结果小圆比小方早2分钟到达处,两人均匀速运动,如图是两人距处路程(米)与时间(分钟)之间的函数图象.根据上述信息,下列说法错误的是( )
A.小方的速度为米/分钟
B.小圆的速度为300米/分钟
C.线段所在直线函数解析式为
D.出发分钟或分钟后,两人之间路程相距200米
4.如图,点A的坐标为,点在直线上运动,当线段最短时,点的坐标为( )
A. B. C. D.
5.如图,矩形的边在轴上,的中点与原点重合,,过定点和动点的直线与矩形的边有公共点,则的取值范围是( )
A. B. C. D.
6.若直线与x轴交点的横坐标为1,则关于x的方程的解为( )
A. B. C. D.
7.为了保护学生视力,课桌高度与凳子高度按照的关系配套设计,那么高的凳子应配课桌的高度为( )
A. B. C. D.
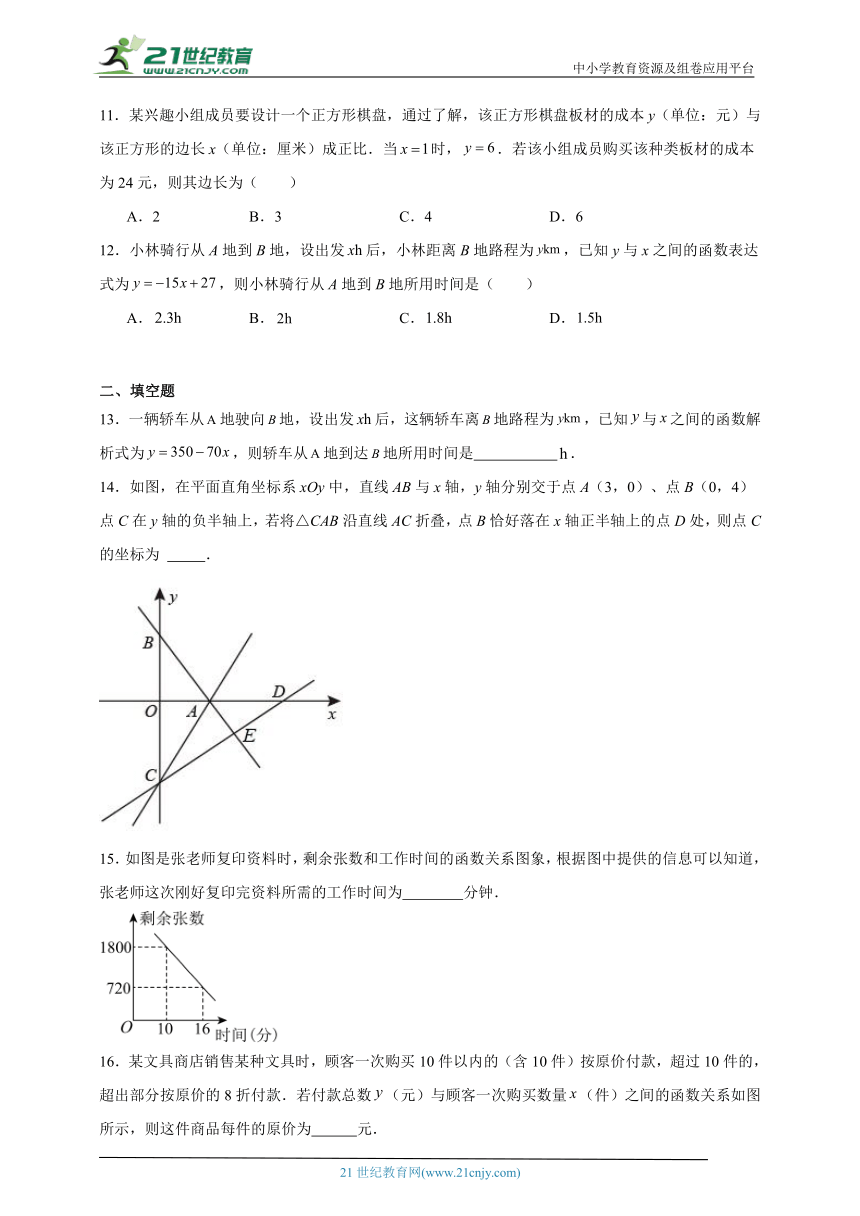
8.数形结合是数学解题中常用的思想方法,使用数形结合的方法,很多问题可迎刃而解,且解法简洁.如图,已知一次函数和的图象交于点,根据图象可得,关于x的方程的解为( )
A. B. C. D.
9.如图,A、B两站相距42千米,甲骑自行车匀速行驶,由A站经P处去B站,上午8时,甲位于距A站18千米处的P处,若再向前行驶15分钟,使可到达距A站22千米处.设甲从P处出发x小时,距A站y千米,则y与x之间的关系可用图象表示为 ( )
A. B. C. D.
10.一个有进水管与出水管的容器,从某时刻开始内只进水不出水,在随后的内既进水又出水,每分的进水量和出水量是两个常数.容器内的水量y(单位:L)与时间x(单位:)之间的关系如图所示,当时,y的值为( )
A.40L B.421 C.44L D.46L
11.某兴趣小组成员要设计一个正方形棋盘,通过了解,该正方形棋盘板材的成本y(单位:元)与该正方形的边长x(单位:厘米)成正比.当时,.若该小组成员购买该种类板材的成本为24元,则其边长为( )
A.2 B.3 C.4 D.6
12.小林骑行从A地到B地,设出发后,小林距离B地路程为,已知y与x之间的函数表达式为,则小林骑行从A地到B地所用时间是( )
A. B. C. D.
二、填空题
13.一辆轿车从地驶向地,设出发后,这辆轿车离地路程为,已知与之间的函数解析式为,则轿车从地到达地所用时间是 .
14.如图,在平面直角坐标系xOy中,直线AB与x轴,y轴分别交于点A(3,0)、点B(0,4)点C在y轴的负半轴上,若将△CAB沿直线AC折叠,点B恰好落在x轴正半轴上的点D处,则点C的坐标为 .
15.如图是张老师复印资料时,剩余张数和工作时间的函数关系图象,根据图中提供的信息可以知道,张老师这次刚好复印完资料所需的工作时间为 分钟.
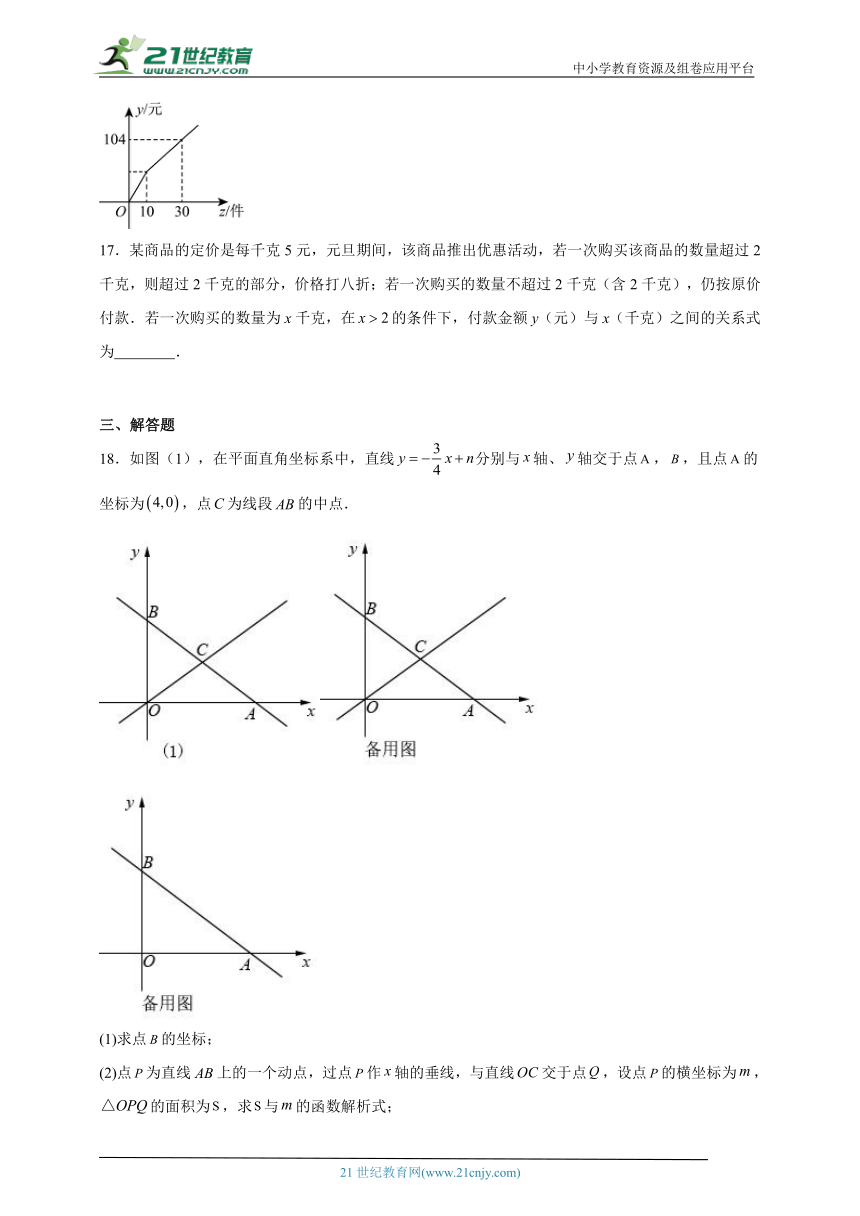
16.某文具商店销售某种文具时,顾客一次购买10件以内的(含10件)按原价付款,超过10件的,超出部分按原价的8折付款.若付款总数(元)与顾客一次购买数量(件)之间的函数关系如图所示,则这件商品每件的原价为 元.
17.某商品的定价是每千克5元,元旦期间,该商品推出优惠活动,若一次购买该商品的数量超过2千克,则超过2千克的部分,价格打八折;若一次购买的数量不超过2千克(含2千克),仍按原价付款.若一次购买的数量为x千克,在的条件下,付款金额y(元)与x(千克)之间的关系式为 .
三、解答题
18.如图(1),在平面直角坐标系中,直线分别与轴、轴交于点,,且点的坐标为,点为线段的中点.
(1)求点的坐标;
(2)点为直线上的一个动点,过点作轴的垂线,与直线交于点,设点的横坐标为,的面积为,求与的函数解析式;
(3)当点在直线上运动时,在平面直角坐标系内是否存在一点,使得以,,,为顶点的四边形为矩形?若存在,直接写出点的坐标;若不存在,请说明理由.
19.已知一次函数的图象如图所示.
(1)关于x的方程的解是________;
(2)关于x的方程的解是________;
(3)关于x的方程的解是________.
20.周六上午小明从家出发,乘车1小时到郊外某基地参加社会实践活动,在基地活动2.2小时后,因家里有急事,他立即按原路以4千米/时的平均速度步行返回.同时爸爸开车从家出发沿同一路线接他,在离家28千米处与小明相遇.接到小明后保持车速不变,立即按原路返回.设小明离开家的时间为x小时,小名离家的路程y (千米) 与x (小时)之间的函数图象如图所示,
(1)小明去基地乘车的平均速度是________千米/小时,爸爸开车的平均速度应是________千米/小时;
(2)求线段所表示的函数关系式;
(3)问小明能否在前回到家?若能,请说明理由:若不能,请算出时他离家的路程,
21.某水果经销商以10元/千克的价格向当地果农收购某种水果,该水果的市场销售价为20元/千克,根据市场调查,经销商决定降价销售.已知这种水果日销售量y(千克)与每千克降价x(元)(0≤x<10)之间满足如图所示的一次函数关系.
(1)求y与x之间的关系式;
(2)若经销商计划该种水果每日获利440元,那么该种水果每千克应降价多少元进行销售?其相应的日销售量为多少?
22.如图1,已知直线与x轴交于点A,与y轴交于点B,直线l2与y轴交于点,与直线l1交于点D(2,t).
(1)求直线l2的解析式;
(2)如图2,若点P在直线l1上,过点P作轴交l2于点Q,交x轴于点G,使,求此时P点的坐标;
(3)将直线向左平移10个单位得到直线l3交x轴于点E,点F是点C关于原点的对称点,过点F作直线轴.在直线l4上是否存在动点M,使得为等腰三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
23.甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与行驶时间x(小时)之间的函数关系如图所示,已知甲对应的函数关系式为,根据图象提供的信息,解决下列问题:
(1)求乙离开A城的距离y与x的关系式;
(2)求乙出发后几小时追上甲车?
(3)从图象上看,x为何值时,两车之间的路程最大?通过计算说明,最大路程是多少千米?
24.如图,一次函数的图象分别与轴,轴的正半轴交于点、,一次函数的图象与直线交于点,且交于轴于点.
(1)求的值及点、的坐标;
(2)求的面积;
(3)若点是轴上的一个动点,当时,求出点的坐标.
《4.4一次函数的应用》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C D D B D A A A A D
题号 11 12
答案 C C
1.C
【分析】本题主要考查了一次函数与一元一次方程之间的关系.一次函数图象与x轴交点的横坐标等于对应方程的解,据此即可解答.
【详解】解:一次函数的图象与轴交于点,
关于的方程的解为,
故选:C.
2.D
【分析】本题主要考查一次函数的应用,理解函数图象是解题关键.根据函数关系图得出后,甲的路程比乙的路程远,可判断A; 根据图象可知,甲走了,所以甲的平均速度为,即可判断B;观察函数关系图即可得前时,乙的速度比甲快 ,即可判断C; 观察函数关系图经过,甲、乙走的路程,即可判断D.
【详解】解∶ A.后,甲的路程比乙的路程远, 故A不符合题意;
B.根据图象可知, 甲走了,所以甲的平均速度为,故B不符合题意;
C.前,甲走了,乙走了,所以乙比甲的速度快,故C不符合题意;
D.经过,由函数图象可知,甲、乙都走了,故D符合题意.
故选∶ D
3.D
【分析】本题考查一次函数的应用、路程速度时间的关系等知识,利用速度路程时间,找准小方、小圆的路程和时间,可求出小方、小圆的速度;得出点G的坐标,设直线的解析式为:,将F,G的坐标代入,求解方程组即可得线段所在直线函数解析式;两人之间路程相距200米,根据题意可知存在三种情况,然后分别计算即可.
【详解】解:根据题意可知,,
∴小圆的速度为:(米/分钟),
故选项B正确;
∴小圆从B地到C地用时:(分钟),
∴,
∴,
∴小方的速度为(米/分钟),
故选项A正确;
设线段所在直线函数解析式为,
将、代入,
得,
解得,
∴线段所在直线函数解析式为,
故选项C正确;
由题意可知,相距300米,相距900米,
∵,,
∴直线的解析式为:,
∵,
∴直线的解析式为:,
当时,小方从处徒步前往处,同时小圆从处骑车前往处,即小方、小圆朝相反方向走,
∴令,
解得,
∵当时,小方从处徒步前往处,小圆从处往处骑行,
∴,
解得(不合题意,舍去),
∵当时,小方从继续徒步前往处,小圆从处往处骑行,
∴或,
解得或.
综上,出发分钟或分钟或分钟后,两人之间的路程相距200米,
故选项D错误.
故选:D.
4.B
【分析】过点B作轴于C,作轴于D,得四边形是正方形,当线段垂直直线时,线段最短,,根据直线是二、四象限角平分线,得,得,根据点A的坐标为,得,即得点B的坐标为.
【详解】当线段垂直直线时,线段最短,,
过点B作轴于C,作轴于D,
则,
∵直线是二、四象限角平分线,
∴,
∵,
∴四边形是正方形,
∵,
∴是等腰直角三角形,
∴,
∵点A的坐标为,
∴,
∴,
∴,
∴点B的坐标为:.
故选:B.
【点睛】此题考查了正比例函数的性质,等腰直角三角形的判定与性质,角平分线判定和性质,正方形的判定和性质.熟练掌握是解题的关键.
5.D
【分析】考查了一次函数的综合题,解题关键是运用数形结合思想.分别求出直线过点D和直线过点C时对应的函数解析式,然后求出点P的坐标即可.
【详解】解:根据题意得:,即,
当直线过点D时,设直线的解析式为,
将点代入得:,
解得,
∴直线的解析式为,
令,得到;
当直线过点C时,设直线的解析式为,
将点代入得:,
解得,
∴直线的解析式为,
令,得,
则过定点和动点的直线与矩形的边有公共点时,a的取值范围是.
故选:D.
6.A
【分析】本题考查了一次函数的性质与一元一次方程,一次函数与轴的交点问题,由直线与x轴交点的横坐标为1,得到,将代入中,即可求解,掌握相关知识是解题的关键.
【详解】解:∵直线与x轴交点的横坐标为1,
∴,
∴,
将代入中,得:,
∴,
∵,
∴,
故选:A.
7.A
【分析】本题主要考查了一次函数的应用,把代入,求出结果即可.
【详解】解:把代入得:
,
即高的凳子应配课桌的高度为,
故选:A.
8.A
【分析】本题考查了利用图象法解一元一次方程,根据一次函数和的图象交于点即可得解,采用数形结合的思想是解此题的关键.
【详解】解:∵一次函数和的图象交于点,
∴根据图象可得,关于x的方程的解为,
故选:A.
9.A
【分析】本题考查了一次函数的应用.首先根据题意,得出、所表示的意义(注意单位),然后再计算出甲1.5小时行驶的路程,结合的初始位置来判断各选项的对错.
【详解】解:由题意,知:甲15分钟即小时行驶了千米,
所以甲的速度为:千米小时;
故甲从行驶1.5小时后,距地的距离为千米,可排除B、D选项;
由于处距地18千米,且甲从处出发,故的初始值应该是18,可排除C选项;
故选:A.
10.D
【分析】本题主要考查了一次函数的应用.依据题意,先求出时的函数关系式,然后将代入计算可以得解.
【详解】解:设当时的直线解析式为:.
图象过、,
可得.解得.
直线解析式为.
令,
.
故选:D.
11.C
【分析】本题考查待定系数法求正比例函数解析式,理解题意求出正比例函数解析式是解题的关键.
先由题意设,用待定系数法求出k的值,再将代入解析式计算即可得到边长.
【详解】解:根据题意设,
当时,,
,
,
当时,,解得,
因此,边长为4厘米.
故选C.
12.C
【分析】本题考查了一次函数的应用.
根据“小林距离B地路程为”结合求解即可.
【详解】解:∵小林距离B地路程为,
∴当小林骑行从A地到达B地时,,
此时
解得:
故选:C.
13.
【分析】本题考查一次函数的应用,理解题意,根据题意将代入解析式,直接求解即可.
【详解】解:根据题意得:当时,时,
解得:,
故答案为:.
14.(0,-6)
【分析】利用勾股定理可得AB=5,由折叠得:AD=AB=5,得出点D的坐标,设点C(0,m),则OC=-m,由勾股定理代入计算即可得出结果.
【详解】解:∵A(3,0)、B(0,4),
∴OA=3,OB=4,
∵∠AOB=90°,
∴AB=,
由折叠得:AD=AB=5,
∴OD=OA+AD=3+5=8,
∴点D(8,0),
设点C(0,m),则OC=-m,
由折叠得:CD=BC=4-m,
在Rt OCD中,
,
∴,
解得:m=-6,
∴C(0,-6),
故答案为:(0,-6).
【点睛】题目主要考查一次函数的综合应用,解答本题的关键是利用翻折的性质、勾股定理及待定系数法确定函数解析式.
15.20
【分析】本题主要考查了一次函数的实际应用.利用待定系数法求出函数解析式,即可求解.
【详解】解:根据题意得:剩余张数和工作时间的函数关系是一次函数关系,
设该函数解析式为,
把点代入得:
,
解得:,
∴该函数解析式为,
当时,,
解得:,
即张老师这次刚好复印完资料所需的工作时间为20分钟.
故答案为:20
16.4
【分析】设这件商品每件的原价为a元,当购买的件数x超过10件时,所付的款数,再根据点在一次函数的图象上得,由此解出a即可得出答案.
此题主要考查了一次函数的应用,理解题意,正确的列出,当购买的件数x超过10件时,所付的款数元与件之间的函数关系,读懂函数的图象,并从函数的图象中获取准确的解题信息是解决问题的关键.
【详解】解:设这件商品每件的原价为a元,
当购买的件数x超过10件时,所付的款数,
整理得:,
根据元与件之间的函数关系可知:点在一次函数的图象上,
,
解得:
答:这件商品每件的原价为4元.
故答案为4.
17.
【分析】本题考查了一次函数的实际应用知识,掌握以上知识并充分理解题意是解答本题的关键.
本题当时,付款金额由两部分构成,一部分是2千克所花的钱,另一部分是超过2千克所花的钱,然后即可求解.
【详解】解:由题意可列式:当,即.
故答案为:
18.(1)点
(2)
(3)存在,点为或
【分析】(1)用待定系数法即可求解;
(2)S=PQ |xP|,即可求解;
(3)分OB是矩形的边、OB是矩形的对角线两种情况,分别求解即可.
【详解】(1)将点代入,得,解得,
∴直线的表达式为,
当时,,
∴点.
(2)∵点为线段的中点,,,
∴,
设直线OC的表达式为y=px,将代入得:,
∴则直线的表达式为:,
∵点的横坐标为,且点为直线上的点,
将代入,得到,
又∵轴,
∴,
∴,
当点在轴右侧,且在点右侧时,
,
当点在轴右侧,且与点重合时,
当点在轴右侧,且在点左侧时,
,
当点在轴左侧时,,
当点在轴上时,.
综上,
(3)设P(m,-m+3),点N(s,t),而点O、B的坐标分别为(0,0)、(0,3);
①当OB是矩形的边时,
则点P与点A重合,故点P(4,0),故点N(4,3);
②当OB是矩形的对角线时,
由中点公式得:m+s=0且-m+3+t=3+0①,
由矩形的对角线相等得:OB=PN,即(m-s)2+(-m+3-t)2=32②,
联立①②并解得:,
∴,
故点;
综上,点P的坐标为(4,0)或.
【点睛】本题考查的是一次函数综合运用,涉及到矩形的性质、面积的计算等,其中(2)、(3),要注意分类求解,避免遗漏.
19.(1)
(2)
(3)
【分析】此题主要考查了一次函数与方程,关键是正确利用数形结合的方法从图象中找到正确答案.
(1)一次函数的图象与轴交点横坐标的值即为方程的解;
(2)根据一次函数图象可得一次函数的图象经过点,进而得到方程的解;
(3)根据一次函数图象可得一次函数的图象经过点,进而得到方程的解.
【详解】(1)解: 一次函数的图象与轴相交于点,
关于的方程的解是.
故答案为:;
(2)解:根据图象可得,一次函数的图象经过点,
因此关于的方程的解,
故答案为:;
(3)解:根据图象可得,一次函数的图象经过点,
因此关于的方程的解,
故答案为:.
20.(1)30,56
(2)线段的表达式:
(3)不能,理由见解析
【分析】本题主要考查了一次函数的实际应用,解答一次函数的应用问题中,要注意自变量的取值范围还必须使实际问题有意义,属于中档题.
(1)仔细观察图象,结合题意即可得出答案;
(2)先设一次函数的解析式,然后将两点坐标代入解析式即可得出线段所表示的函数关系式;
(3)根据图象和解析式可知小明从出发到回家一共需要4.2小时,故前不能回到家.
【详解】(1)解:仔细观察图象可知:小明去基地乘车1小时后离基地的距离为30千米,
因此小明去基地乘车的平均速度是30千米小时,
在返回时小明以4千米时的平均速度步行,行驶2千米后遇到爸爸,
因两个人同时走,小明走了0.5小时,即爸爸也走了0.5小时
他爸爸在0.5小时内行驶了28千米,
故爸爸开车的平均速度应是56千米小时;
故答案为:30,56;
(2)解:线段所表示的函数关系式为;
点的横坐标为:,
,
点横坐标是:,
;
将两点代入函数解析式即可得线段的表达式:;
(3)解:不能.
小明从家出发到回家一共需要时间:(小时),
从经过4.2小时已经过了,
不能在前回到家,此时离家的距离:(千米).
21.(1)
(2)6元,110千克
【分析】(1)根据图象上点的坐标,利用待定系数法求一次函数解析式即可;
(2)每日利润=每千克销售利润×日销售量,由此可得关于x的一元二次方程,求出x的值,代入y与x之间的关系式即可求出相应的日销售量.
【详解】(1)解:设y与x之间的关系式为,
观察图象,将,代入得,
解得,
故y与x之间的关系式为;
(2)解:依题意,降价x元后,每千克销售利润为元,日销量为千克,
则,
整理得,
解得或(不合题意,舍去)
当时,,
故该种水果每千克应降价6元进行销售,其相应的日销售量为110千克.
【点睛】本题考查一次函数和一元二次方程的实际应用,第1问需要掌握利用待定系数法求一次函数的解析式,关键是从图象中找出有用信息;第2问关键是根据题意找出等量关系列方程并正确求解.
22.(1),(2);(3)或,或
【分析】(1)把点D坐标代入直线求出t的值,运用待定系数法求出l2即可;
(2)根据三角形面积公式求解即可;
(3)设 则,分,,三种情况列式求解即可.
【详解】解:(1)∵D(2,t)在直线
∴,
∴D(2,3)
设直线的解析式为,
将点C,D代入得,
解得,
所以,线的解析式为
(2)设
∵PQ//x轴,
∴G(a,0),Q(a,2a-1)
∵,且
∴
∴
解得,,(舍去)
∴
(3)存在,理由如下:
对于直线
当时,;当时,
∴,
∴
如图,
∵
∴
又∵
∴
∴的解析式为:
设 则
当为等腰三角形,有:
①时,
解得,,即
②时,
解得:或
即,
③时,
解得,或(舍去)
即
综上,点M的坐标为:或,或.
【点睛】本题为一次函数综合运用题,解题的关键是熟练掌握待定系数法求函数解析式、等腰三角形的性质等知识,其中(3)要注意分类求解,避免遗漏.
23.(1)
(2)乙车出发后1.5小时追上甲车
(3)相遇前、相遇后时两车之间的路程最大,最大路程60千米
【分析】(1)设乙对应的函数关系式为,利用待定系数法求解即可确定函数解析式;
(2)联立甲乙两车对应的函数解析式求解即可;
(3)结合图象,相遇前、相遇后时两车之间的路程最大,代入求解即可.
【详解】(1)解:设乙对应的函数关系式为
将点(4,300),(1,0)代入得:
解得:
∴乙对应的函数关系式;
(2)联立两个函数得:
解得:
(小时)
∴乙车出发后1.5小时追上甲车;
(3)从图上看,相遇前、相遇后时两车之间的路程最大
当时,两车之间的路程是(千米)
当时,两车之间的路程是(60千米).
【点睛】题目主要考查利用待定系数法确定一次函数解析式,从函数图象获取相关信息,求函数值等,理解题意,从函数图象获取相关信息是解题关键.
24.(1),,;
(2)2
(3)点的坐标为或
【分析】(1)根据函数值,可得相应自变量的值,根据自变量的值,可得相应的函数值;
(2)根据待定系数法,可得的解析式,根据函数值为零,可得点坐标,根据三角形的面积公式,可得答案;
(3)设,可得,然后根据时,即可求出点的坐标.
【详解】(1)解:一次函数的图象经过点,
得,
解得,
一次函数的图象分别与轴,轴的正半轴交于点、,
当时,,
解得,即,
当时,,即,
,,;
(2)解:把点一次函数,得,解得,
,
当时,,即.
,
;
(3)解:点是轴上的一个动点,设,
,
,
,
或,
点的坐标为或.
【点睛】本题考查了两条直线相交或平行问题,一次函数的性质,(1)利用了自变量与函数值的对应关系,(2)利用了三角形的面积公式,(3)利用了分类讨论的方法,掌握一次函数的性质是解题关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
4.4一次函数的应用
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.一次函数与轴相交于点,则关于的方程的解为( )
A. B. C. D.无法求解
2.甲、乙两位同学放学后走路回家,他们走过的路程(单位:)与所用的时间(单位:)之间的关系如图所示.根据图中信息,下列说法正确的是( )
A.乙走的路程比甲远
B.甲的平均速度为
C.前,甲的速度比乙快
D.经过,甲、乙都走了
3.在一条沿山而建的游览路线上依次有三处观景台,小方从处徒步前往处,同时小圆从处骑车前往处,到达处后休息1分钟,然后立即折返(折返时间忽略不计)按原路原速前往处,结果小圆比小方早2分钟到达处,两人均匀速运动,如图是两人距处路程(米)与时间(分钟)之间的函数图象.根据上述信息,下列说法错误的是( )
A.小方的速度为米/分钟
B.小圆的速度为300米/分钟
C.线段所在直线函数解析式为
D.出发分钟或分钟后,两人之间路程相距200米
4.如图,点A的坐标为,点在直线上运动,当线段最短时,点的坐标为( )
A. B. C. D.
5.如图,矩形的边在轴上,的中点与原点重合,,过定点和动点的直线与矩形的边有公共点,则的取值范围是( )
A. B. C. D.
6.若直线与x轴交点的横坐标为1,则关于x的方程的解为( )
A. B. C. D.
7.为了保护学生视力,课桌高度与凳子高度按照的关系配套设计,那么高的凳子应配课桌的高度为( )
A. B. C. D.
8.数形结合是数学解题中常用的思想方法,使用数形结合的方法,很多问题可迎刃而解,且解法简洁.如图,已知一次函数和的图象交于点,根据图象可得,关于x的方程的解为( )
A. B. C. D.
9.如图,A、B两站相距42千米,甲骑自行车匀速行驶,由A站经P处去B站,上午8时,甲位于距A站18千米处的P处,若再向前行驶15分钟,使可到达距A站22千米处.设甲从P处出发x小时,距A站y千米,则y与x之间的关系可用图象表示为 ( )
A. B. C. D.
10.一个有进水管与出水管的容器,从某时刻开始内只进水不出水,在随后的内既进水又出水,每分的进水量和出水量是两个常数.容器内的水量y(单位:L)与时间x(单位:)之间的关系如图所示,当时,y的值为( )
A.40L B.421 C.44L D.46L
11.某兴趣小组成员要设计一个正方形棋盘,通过了解,该正方形棋盘板材的成本y(单位:元)与该正方形的边长x(单位:厘米)成正比.当时,.若该小组成员购买该种类板材的成本为24元,则其边长为( )
A.2 B.3 C.4 D.6
12.小林骑行从A地到B地,设出发后,小林距离B地路程为,已知y与x之间的函数表达式为,则小林骑行从A地到B地所用时间是( )
A. B. C. D.
二、填空题
13.一辆轿车从地驶向地,设出发后,这辆轿车离地路程为,已知与之间的函数解析式为,则轿车从地到达地所用时间是 .
14.如图,在平面直角坐标系xOy中,直线AB与x轴,y轴分别交于点A(3,0)、点B(0,4)点C在y轴的负半轴上,若将△CAB沿直线AC折叠,点B恰好落在x轴正半轴上的点D处,则点C的坐标为 .
15.如图是张老师复印资料时,剩余张数和工作时间的函数关系图象,根据图中提供的信息可以知道,张老师这次刚好复印完资料所需的工作时间为 分钟.
16.某文具商店销售某种文具时,顾客一次购买10件以内的(含10件)按原价付款,超过10件的,超出部分按原价的8折付款.若付款总数(元)与顾客一次购买数量(件)之间的函数关系如图所示,则这件商品每件的原价为 元.
17.某商品的定价是每千克5元,元旦期间,该商品推出优惠活动,若一次购买该商品的数量超过2千克,则超过2千克的部分,价格打八折;若一次购买的数量不超过2千克(含2千克),仍按原价付款.若一次购买的数量为x千克,在的条件下,付款金额y(元)与x(千克)之间的关系式为 .
三、解答题
18.如图(1),在平面直角坐标系中,直线分别与轴、轴交于点,,且点的坐标为,点为线段的中点.
(1)求点的坐标;
(2)点为直线上的一个动点,过点作轴的垂线,与直线交于点,设点的横坐标为,的面积为,求与的函数解析式;
(3)当点在直线上运动时,在平面直角坐标系内是否存在一点,使得以,,,为顶点的四边形为矩形?若存在,直接写出点的坐标;若不存在,请说明理由.
19.已知一次函数的图象如图所示.
(1)关于x的方程的解是________;
(2)关于x的方程的解是________;
(3)关于x的方程的解是________.
20.周六上午小明从家出发,乘车1小时到郊外某基地参加社会实践活动,在基地活动2.2小时后,因家里有急事,他立即按原路以4千米/时的平均速度步行返回.同时爸爸开车从家出发沿同一路线接他,在离家28千米处与小明相遇.接到小明后保持车速不变,立即按原路返回.设小明离开家的时间为x小时,小名离家的路程y (千米) 与x (小时)之间的函数图象如图所示,
(1)小明去基地乘车的平均速度是________千米/小时,爸爸开车的平均速度应是________千米/小时;
(2)求线段所表示的函数关系式;
(3)问小明能否在前回到家?若能,请说明理由:若不能,请算出时他离家的路程,
21.某水果经销商以10元/千克的价格向当地果农收购某种水果,该水果的市场销售价为20元/千克,根据市场调查,经销商决定降价销售.已知这种水果日销售量y(千克)与每千克降价x(元)(0≤x<10)之间满足如图所示的一次函数关系.
(1)求y与x之间的关系式;
(2)若经销商计划该种水果每日获利440元,那么该种水果每千克应降价多少元进行销售?其相应的日销售量为多少?
22.如图1,已知直线与x轴交于点A,与y轴交于点B,直线l2与y轴交于点,与直线l1交于点D(2,t).
(1)求直线l2的解析式;
(2)如图2,若点P在直线l1上,过点P作轴交l2于点Q,交x轴于点G,使,求此时P点的坐标;
(3)将直线向左平移10个单位得到直线l3交x轴于点E,点F是点C关于原点的对称点,过点F作直线轴.在直线l4上是否存在动点M,使得为等腰三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
23.甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与行驶时间x(小时)之间的函数关系如图所示,已知甲对应的函数关系式为,根据图象提供的信息,解决下列问题:
(1)求乙离开A城的距离y与x的关系式;
(2)求乙出发后几小时追上甲车?
(3)从图象上看,x为何值时,两车之间的路程最大?通过计算说明,最大路程是多少千米?
24.如图,一次函数的图象分别与轴,轴的正半轴交于点、,一次函数的图象与直线交于点,且交于轴于点.
(1)求的值及点、的坐标;
(2)求的面积;
(3)若点是轴上的一个动点,当时,求出点的坐标.
《4.4一次函数的应用》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C D D B D A A A A D
题号 11 12
答案 C C
1.C
【分析】本题主要考查了一次函数与一元一次方程之间的关系.一次函数图象与x轴交点的横坐标等于对应方程的解,据此即可解答.
【详解】解:一次函数的图象与轴交于点,
关于的方程的解为,
故选:C.
2.D
【分析】本题主要考查一次函数的应用,理解函数图象是解题关键.根据函数关系图得出后,甲的路程比乙的路程远,可判断A; 根据图象可知,甲走了,所以甲的平均速度为,即可判断B;观察函数关系图即可得前时,乙的速度比甲快 ,即可判断C; 观察函数关系图经过,甲、乙走的路程,即可判断D.
【详解】解∶ A.后,甲的路程比乙的路程远, 故A不符合题意;
B.根据图象可知, 甲走了,所以甲的平均速度为,故B不符合题意;
C.前,甲走了,乙走了,所以乙比甲的速度快,故C不符合题意;
D.经过,由函数图象可知,甲、乙都走了,故D符合题意.
故选∶ D
3.D
【分析】本题考查一次函数的应用、路程速度时间的关系等知识,利用速度路程时间,找准小方、小圆的路程和时间,可求出小方、小圆的速度;得出点G的坐标,设直线的解析式为:,将F,G的坐标代入,求解方程组即可得线段所在直线函数解析式;两人之间路程相距200米,根据题意可知存在三种情况,然后分别计算即可.
【详解】解:根据题意可知,,
∴小圆的速度为:(米/分钟),
故选项B正确;
∴小圆从B地到C地用时:(分钟),
∴,
∴,
∴小方的速度为(米/分钟),
故选项A正确;
设线段所在直线函数解析式为,
将、代入,
得,
解得,
∴线段所在直线函数解析式为,
故选项C正确;
由题意可知,相距300米,相距900米,
∵,,
∴直线的解析式为:,
∵,
∴直线的解析式为:,
当时,小方从处徒步前往处,同时小圆从处骑车前往处,即小方、小圆朝相反方向走,
∴令,
解得,
∵当时,小方从处徒步前往处,小圆从处往处骑行,
∴,
解得(不合题意,舍去),
∵当时,小方从继续徒步前往处,小圆从处往处骑行,
∴或,
解得或.
综上,出发分钟或分钟或分钟后,两人之间的路程相距200米,
故选项D错误.
故选:D.
4.B
【分析】过点B作轴于C,作轴于D,得四边形是正方形,当线段垂直直线时,线段最短,,根据直线是二、四象限角平分线,得,得,根据点A的坐标为,得,即得点B的坐标为.
【详解】当线段垂直直线时,线段最短,,
过点B作轴于C,作轴于D,
则,
∵直线是二、四象限角平分线,
∴,
∵,
∴四边形是正方形,
∵,
∴是等腰直角三角形,
∴,
∵点A的坐标为,
∴,
∴,
∴,
∴点B的坐标为:.
故选:B.
【点睛】此题考查了正比例函数的性质,等腰直角三角形的判定与性质,角平分线判定和性质,正方形的判定和性质.熟练掌握是解题的关键.
5.D
【分析】考查了一次函数的综合题,解题关键是运用数形结合思想.分别求出直线过点D和直线过点C时对应的函数解析式,然后求出点P的坐标即可.
【详解】解:根据题意得:,即,
当直线过点D时,设直线的解析式为,
将点代入得:,
解得,
∴直线的解析式为,
令,得到;
当直线过点C时,设直线的解析式为,
将点代入得:,
解得,
∴直线的解析式为,
令,得,
则过定点和动点的直线与矩形的边有公共点时,a的取值范围是.
故选:D.
6.A
【分析】本题考查了一次函数的性质与一元一次方程,一次函数与轴的交点问题,由直线与x轴交点的横坐标为1,得到,将代入中,即可求解,掌握相关知识是解题的关键.
【详解】解:∵直线与x轴交点的横坐标为1,
∴,
∴,
将代入中,得:,
∴,
∵,
∴,
故选:A.
7.A
【分析】本题主要考查了一次函数的应用,把代入,求出结果即可.
【详解】解:把代入得:
,
即高的凳子应配课桌的高度为,
故选:A.
8.A
【分析】本题考查了利用图象法解一元一次方程,根据一次函数和的图象交于点即可得解,采用数形结合的思想是解此题的关键.
【详解】解:∵一次函数和的图象交于点,
∴根据图象可得,关于x的方程的解为,
故选:A.
9.A
【分析】本题考查了一次函数的应用.首先根据题意,得出、所表示的意义(注意单位),然后再计算出甲1.5小时行驶的路程,结合的初始位置来判断各选项的对错.
【详解】解:由题意,知:甲15分钟即小时行驶了千米,
所以甲的速度为:千米小时;
故甲从行驶1.5小时后,距地的距离为千米,可排除B、D选项;
由于处距地18千米,且甲从处出发,故的初始值应该是18,可排除C选项;
故选:A.
10.D
【分析】本题主要考查了一次函数的应用.依据题意,先求出时的函数关系式,然后将代入计算可以得解.
【详解】解:设当时的直线解析式为:.
图象过、,
可得.解得.
直线解析式为.
令,
.
故选:D.
11.C
【分析】本题考查待定系数法求正比例函数解析式,理解题意求出正比例函数解析式是解题的关键.
先由题意设,用待定系数法求出k的值,再将代入解析式计算即可得到边长.
【详解】解:根据题意设,
当时,,
,
,
当时,,解得,
因此,边长为4厘米.
故选C.
12.C
【分析】本题考查了一次函数的应用.
根据“小林距离B地路程为”结合求解即可.
【详解】解:∵小林距离B地路程为,
∴当小林骑行从A地到达B地时,,
此时
解得:
故选:C.
13.
【分析】本题考查一次函数的应用,理解题意,根据题意将代入解析式,直接求解即可.
【详解】解:根据题意得:当时,时,
解得:,
故答案为:.
14.(0,-6)
【分析】利用勾股定理可得AB=5,由折叠得:AD=AB=5,得出点D的坐标,设点C(0,m),则OC=-m,由勾股定理代入计算即可得出结果.
【详解】解:∵A(3,0)、B(0,4),
∴OA=3,OB=4,
∵∠AOB=90°,
∴AB=,
由折叠得:AD=AB=5,
∴OD=OA+AD=3+5=8,
∴点D(8,0),
设点C(0,m),则OC=-m,
由折叠得:CD=BC=4-m,
在Rt OCD中,
,
∴,
解得:m=-6,
∴C(0,-6),
故答案为:(0,-6).
【点睛】题目主要考查一次函数的综合应用,解答本题的关键是利用翻折的性质、勾股定理及待定系数法确定函数解析式.
15.20
【分析】本题主要考查了一次函数的实际应用.利用待定系数法求出函数解析式,即可求解.
【详解】解:根据题意得:剩余张数和工作时间的函数关系是一次函数关系,
设该函数解析式为,
把点代入得:
,
解得:,
∴该函数解析式为,
当时,,
解得:,
即张老师这次刚好复印完资料所需的工作时间为20分钟.
故答案为:20
16.4
【分析】设这件商品每件的原价为a元,当购买的件数x超过10件时,所付的款数,再根据点在一次函数的图象上得,由此解出a即可得出答案.
此题主要考查了一次函数的应用,理解题意,正确的列出,当购买的件数x超过10件时,所付的款数元与件之间的函数关系,读懂函数的图象,并从函数的图象中获取准确的解题信息是解决问题的关键.
【详解】解:设这件商品每件的原价为a元,
当购买的件数x超过10件时,所付的款数,
整理得:,
根据元与件之间的函数关系可知:点在一次函数的图象上,
,
解得:
答:这件商品每件的原价为4元.
故答案为4.
17.
【分析】本题考查了一次函数的实际应用知识,掌握以上知识并充分理解题意是解答本题的关键.
本题当时,付款金额由两部分构成,一部分是2千克所花的钱,另一部分是超过2千克所花的钱,然后即可求解.
【详解】解:由题意可列式:当,即.
故答案为:
18.(1)点
(2)
(3)存在,点为或
【分析】(1)用待定系数法即可求解;
(2)S=PQ |xP|,即可求解;
(3)分OB是矩形的边、OB是矩形的对角线两种情况,分别求解即可.
【详解】(1)将点代入,得,解得,
∴直线的表达式为,
当时,,
∴点.
(2)∵点为线段的中点,,,
∴,
设直线OC的表达式为y=px,将代入得:,
∴则直线的表达式为:,
∵点的横坐标为,且点为直线上的点,
将代入,得到,
又∵轴,
∴,
∴,
当点在轴右侧,且在点右侧时,
,
当点在轴右侧,且与点重合时,
当点在轴右侧,且在点左侧时,
,
当点在轴左侧时,,
当点在轴上时,.
综上,
(3)设P(m,-m+3),点N(s,t),而点O、B的坐标分别为(0,0)、(0,3);
①当OB是矩形的边时,
则点P与点A重合,故点P(4,0),故点N(4,3);
②当OB是矩形的对角线时,
由中点公式得:m+s=0且-m+3+t=3+0①,
由矩形的对角线相等得:OB=PN,即(m-s)2+(-m+3-t)2=32②,
联立①②并解得:,
∴,
故点;
综上,点P的坐标为(4,0)或.
【点睛】本题考查的是一次函数综合运用,涉及到矩形的性质、面积的计算等,其中(2)、(3),要注意分类求解,避免遗漏.
19.(1)
(2)
(3)
【分析】此题主要考查了一次函数与方程,关键是正确利用数形结合的方法从图象中找到正确答案.
(1)一次函数的图象与轴交点横坐标的值即为方程的解;
(2)根据一次函数图象可得一次函数的图象经过点,进而得到方程的解;
(3)根据一次函数图象可得一次函数的图象经过点,进而得到方程的解.
【详解】(1)解: 一次函数的图象与轴相交于点,
关于的方程的解是.
故答案为:;
(2)解:根据图象可得,一次函数的图象经过点,
因此关于的方程的解,
故答案为:;
(3)解:根据图象可得,一次函数的图象经过点,
因此关于的方程的解,
故答案为:.
20.(1)30,56
(2)线段的表达式:
(3)不能,理由见解析
【分析】本题主要考查了一次函数的实际应用,解答一次函数的应用问题中,要注意自变量的取值范围还必须使实际问题有意义,属于中档题.
(1)仔细观察图象,结合题意即可得出答案;
(2)先设一次函数的解析式,然后将两点坐标代入解析式即可得出线段所表示的函数关系式;
(3)根据图象和解析式可知小明从出发到回家一共需要4.2小时,故前不能回到家.
【详解】(1)解:仔细观察图象可知:小明去基地乘车1小时后离基地的距离为30千米,
因此小明去基地乘车的平均速度是30千米小时,
在返回时小明以4千米时的平均速度步行,行驶2千米后遇到爸爸,
因两个人同时走,小明走了0.5小时,即爸爸也走了0.5小时
他爸爸在0.5小时内行驶了28千米,
故爸爸开车的平均速度应是56千米小时;
故答案为:30,56;
(2)解:线段所表示的函数关系式为;
点的横坐标为:,
,
点横坐标是:,
;
将两点代入函数解析式即可得线段的表达式:;
(3)解:不能.
小明从家出发到回家一共需要时间:(小时),
从经过4.2小时已经过了,
不能在前回到家,此时离家的距离:(千米).
21.(1)
(2)6元,110千克
【分析】(1)根据图象上点的坐标,利用待定系数法求一次函数解析式即可;
(2)每日利润=每千克销售利润×日销售量,由此可得关于x的一元二次方程,求出x的值,代入y与x之间的关系式即可求出相应的日销售量.
【详解】(1)解:设y与x之间的关系式为,
观察图象,将,代入得,
解得,
故y与x之间的关系式为;
(2)解:依题意,降价x元后,每千克销售利润为元,日销量为千克,
则,
整理得,
解得或(不合题意,舍去)
当时,,
故该种水果每千克应降价6元进行销售,其相应的日销售量为110千克.
【点睛】本题考查一次函数和一元二次方程的实际应用,第1问需要掌握利用待定系数法求一次函数的解析式,关键是从图象中找出有用信息;第2问关键是根据题意找出等量关系列方程并正确求解.
22.(1),(2);(3)或,或
【分析】(1)把点D坐标代入直线求出t的值,运用待定系数法求出l2即可;
(2)根据三角形面积公式求解即可;
(3)设 则,分,,三种情况列式求解即可.
【详解】解:(1)∵D(2,t)在直线
∴,
∴D(2,3)
设直线的解析式为,
将点C,D代入得,
解得,
所以,线的解析式为
(2)设
∵PQ//x轴,
∴G(a,0),Q(a,2a-1)
∵,且
∴
∴
解得,,(舍去)
∴
(3)存在,理由如下:
对于直线
当时,;当时,
∴,
∴
如图,
∵
∴
又∵
∴
∴的解析式为:
设 则
当为等腰三角形,有:
①时,
解得,,即
②时,
解得:或
即,
③时,
解得,或(舍去)
即
综上,点M的坐标为:或,或.
【点睛】本题为一次函数综合运用题,解题的关键是熟练掌握待定系数法求函数解析式、等腰三角形的性质等知识,其中(3)要注意分类求解,避免遗漏.
23.(1)
(2)乙车出发后1.5小时追上甲车
(3)相遇前、相遇后时两车之间的路程最大,最大路程60千米
【分析】(1)设乙对应的函数关系式为,利用待定系数法求解即可确定函数解析式;
(2)联立甲乙两车对应的函数解析式求解即可;
(3)结合图象,相遇前、相遇后时两车之间的路程最大,代入求解即可.
【详解】(1)解:设乙对应的函数关系式为
将点(4,300),(1,0)代入得:
解得:
∴乙对应的函数关系式;
(2)联立两个函数得:
解得:
(小时)
∴乙车出发后1.5小时追上甲车;
(3)从图上看,相遇前、相遇后时两车之间的路程最大
当时,两车之间的路程是(千米)
当时,两车之间的路程是(60千米).
【点睛】题目主要考查利用待定系数法确定一次函数解析式,从函数图象获取相关信息,求函数值等,理解题意,从函数图象获取相关信息是解题关键.
24.(1),,;
(2)2
(3)点的坐标为或
【分析】(1)根据函数值,可得相应自变量的值,根据自变量的值,可得相应的函数值;
(2)根据待定系数法,可得的解析式,根据函数值为零,可得点坐标,根据三角形的面积公式,可得答案;
(3)设,可得,然后根据时,即可求出点的坐标.
【详解】(1)解:一次函数的图象经过点,
得,
解得,
一次函数的图象分别与轴,轴的正半轴交于点、,
当时,,
解得,即,
当时,,即,
,,;
(2)解:把点一次函数,得,解得,
,
当时,,即.
,
;
(3)解:点是轴上的一个动点,设,
,
,
,
或,
点的坐标为或.
【点睛】本题考查了两条直线相交或平行问题,一次函数的性质,(1)利用了自变量与函数值的对应关系,(2)利用了三角形的面积公式,(3)利用了分类讨论的方法,掌握一次函数的性质是解题关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
