5.3二元一次方程组的应用同步练习(含解析)北师大版数学八年级上册
文档属性
| 名称 | 5.3二元一次方程组的应用同步练习(含解析)北师大版数学八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 744.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-24 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
5.3二元一次方程组的应用
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.为奖励在“缤纷节”汇演中表现突出的同学,班主任派小王到文具店为获奖同学购买奖品. 小王发现,购买15 个文具盒和12支钢笔价格一样;如果在上述基础上少购买2个文具盒,多购买2支钢笔,则购买文具盒比钢笔少花36元. 设文具盒单价为x元,钢笔单价为y元,则符合题意的方程组为( )
A. B.
C. D.
2.我国古代数学古典名著《孙子算经》中记载:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”其大意是:用一根绳子去量一根木条,绳子还剩余4.5尺;将绳子对折再量,木条还剩余1尺;问木条多少尺?如果设木条长为尺,绳子长为尺,则下面所列方程组正确的是( )
A. B. C. D.
3.爸爸骑摩托车带着小明在公路上匀速行驶,小明每隔一段时间看到的里程碑上的数如下:
时刻 9:00 10:00 11:30
里程碑上的数 是一个两位数,它的两个数字之和是6 是一个两位数,它的十位与个位数字与9:00所看到的正好互换了 是一个三位数,它比9:00时看到的两位数中间多了个0
则10:00时看到里程碑上的数是( )
A.15 B.24 C.42 D.51
4.我国古代数学名著《九章算术》中记载:“今有共买琎,人出半,盈四;人出少半,不足三.问人数、琎价各几何?”意思是:一起去买琎(一种像玉的石头),每个人出两,则多4两;每个人出两,则不足3两.问人数、琎的价格分别是多少?如果设人数x人,琎的价格为y两,那么可列成的方程组为( )
A. B. C. D.
5.小李家去年节余5000元,今年可节余9500元,并且今年收入比去年高,支出比去年低,今年的收入与支出各是多少?设去年的收入为元,支出为元,则可列方程组为( )
A. B. C. D.
6.兔年来临,小兰要做玩偶兔子和福袋作为新年礼物,她去市场买了36米布,每米布可以做兔子25只,或者福袋40个,小兰将1只玩偶兔子和2个福袋配成一套礼物,结果发现布没有剩余,恰好配套做成了礼物.若设用x米布做兔子,用y米布做福袋,则可列出方程组为( )
A. B. C. D.
7.有大小两种货车,2辆大货车与3辆小货车一次共可运货15.5吨,5辆大货车与6辆小货车一次共可运货35吨,则每辆小货车一次可运货( )
A.2吨 B.2.5吨 C.3吨 D.3.5吨
8.某生产线现有个工人,一个工人每天可生产6个螺杆或个螺母,1个螺杆和2个螺母为一套,现在要求工人每天生产的螺杆和螺母完整配套而没有剩余,若设安排x个工人生产螺杆,y个工人生产螺母,则列出正确的二元一次方程组为( )
A. B.
C. D.
9.一条铁路线A,B,C三个车站的位置如图所示,已知B,C两车站之间相距500千米.火车从B站出发,向C站方向行驶,经过30分钟,距A站130千米;经过2小时,距A站280千米.火车从B站开出多少时间后可到达C站?( )
A.4小时 B.5小时 C.6小时 D.7小时
10.小明和小亮做加法游戏,小明在一个加数后面多写了一个0,得到的和为242;而小亮在另一个加数后面多写了一个0,得到的和为341,原来的两个加数分别是( )
A.21,32 B.12,23 C.31,22 D.41,42
11.某同学的笔袋中有若干支黑色中性笔和红色中性笔(除笔芯颜色不同外,其他都相同),从中随机取出一支笔,取出的是黑色中性笔的概率,如果再往笔袋中放进6支红色中性笔,这时从中随机取出一支笔是黑色中性笔的概率变为,则笔袋中的黑色中性笔有( ).
A.8支 B.6支 C.4支 D.2支
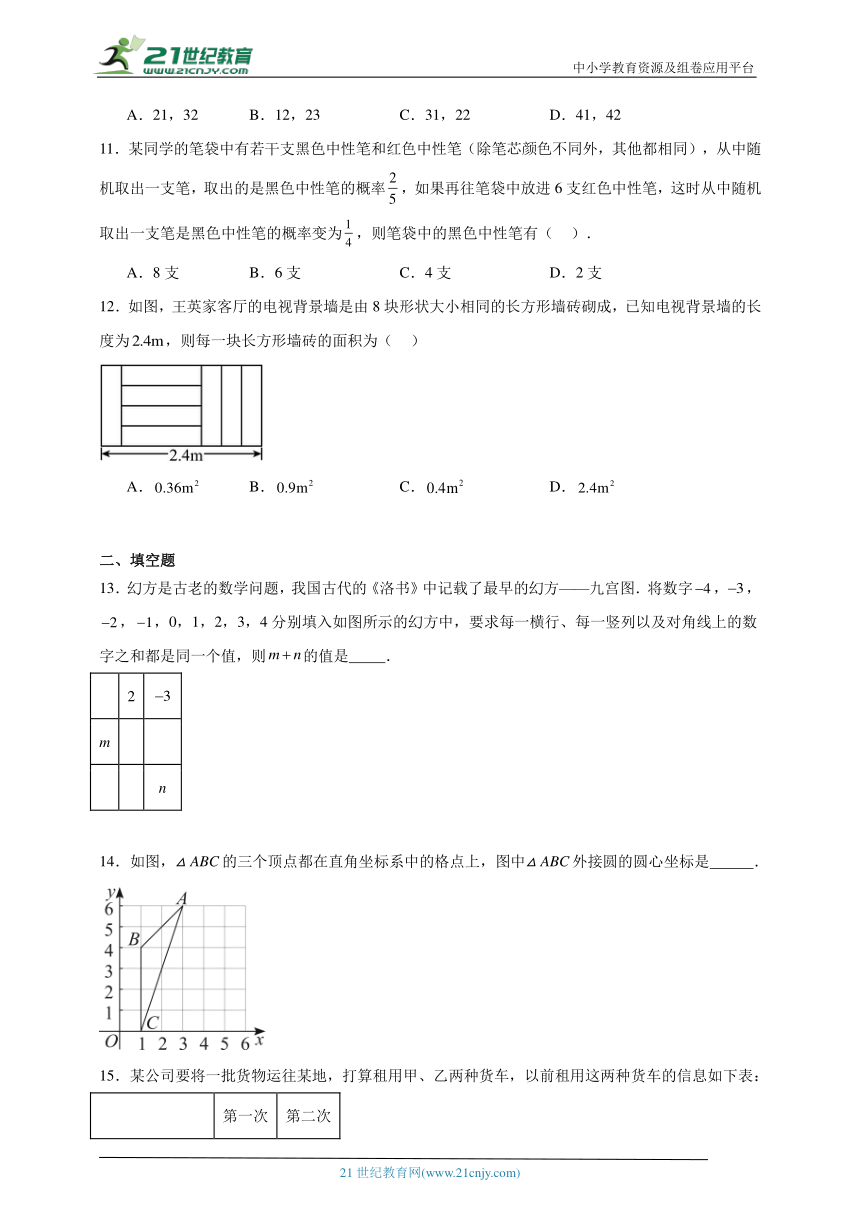
12.如图,王英家客厅的电视背景墙是由8块形状大小相同的长方形墙砖砌成,已知电视背景墙的长度为,则每一块长方形墙砖的面积为( )
A. B. C. D.
二、填空题
13.幻方是古老的数学问题,我国古代的《洛书》中记载了最早的幻方——九宫图.将数字,,,,0,1,2,3,4分别填入如图所示的幻方中,要求每一横行、每一竖列以及对角线上的数字之和都是同一个值,则的值是 .
2
m
n
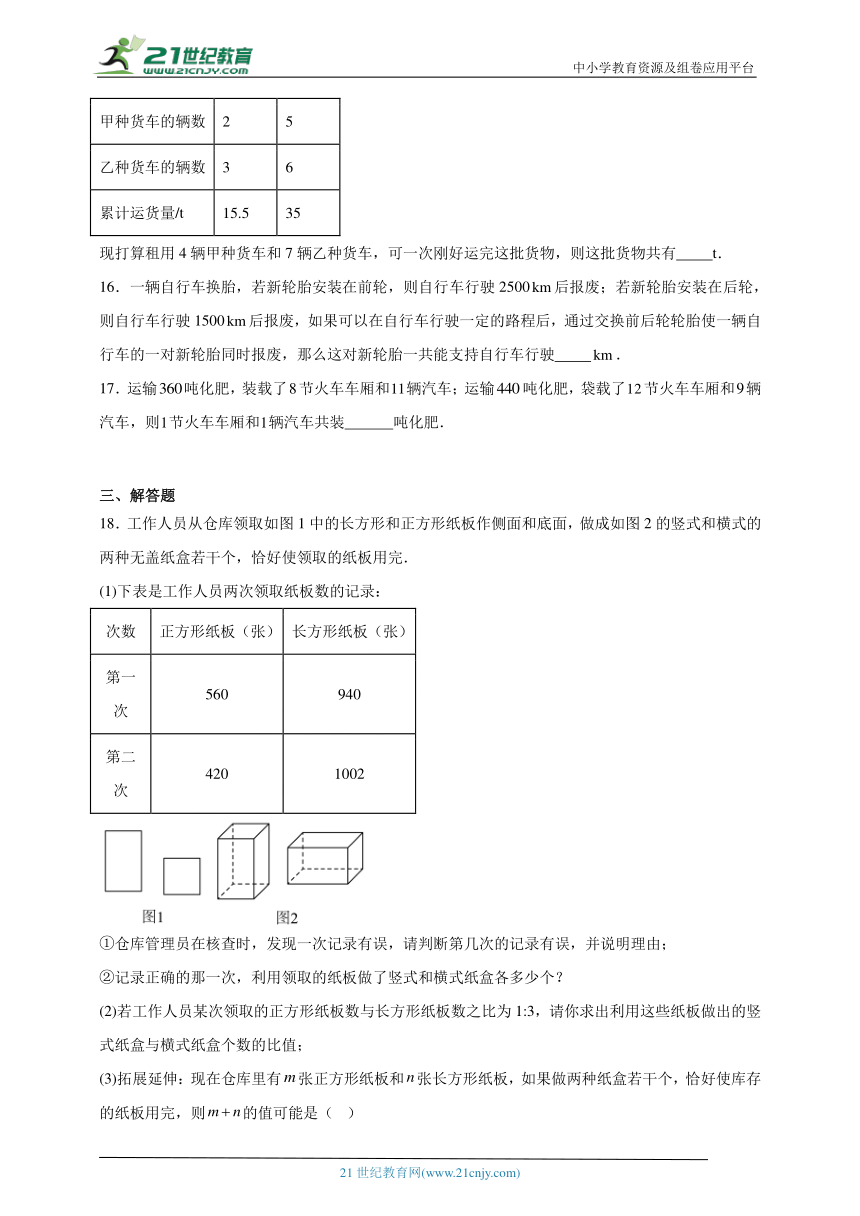
14.如图,△ABC的三个顶点都在直角坐标系中的格点上,图中△ABC外接圆的圆心坐标是 .
15.某公司要将一批货物运往某地,打算租用甲、乙两种货车,以前租用这两种货车的信息如下表:
第一次 第二次
甲种货车的辆数 2 5
乙种货车的辆数 3 6
累计运货量/t 15.5 35
现打算租用4辆甲种货车和7辆乙种货车,可一次刚好运完这批货物,则这批货物共有 t.
16.一辆自行车换胎,若新轮胎安装在前轮,则自行车行驶2500后报废;若新轮胎安装在后轮,则自行车行驶1500后报废,如果可以在自行车行驶一定的路程后,通过交换前后轮轮胎使一辆自行车的一对新轮胎同时报废,那么这对新轮胎一共能支持自行车行驶 .
17.运输吨化肥,装载了节火车车厢和辆汽车;运输吨化肥,袋载了节火车车厢和辆汽车,则节火车车厢和辆汽车共装 吨化肥.
三、解答题
18.工作人员从仓库领取如图1中的长方形和正方形纸板作侧面和底面,做成如图2的竖式和横式的两种无盖纸盒若干个,恰好使领取的纸板用完.
(1)下表是工作人员两次领取纸板数的记录:
次数 正方形纸板(张) 长方形纸板(张)
第一次 560 940
第二次 420 1002
①仓库管理员在核查时,发现一次记录有误,请判断第几次的记录有误,并说明理由;
②记录正确的那一次,利用领取的纸板做了竖式和横式纸盒各多少个?
(2)若工作人员某次领取的正方形纸板数与长方形纸板数之比为1:3,请你求出利用这些纸板做出的竖式纸盒与横式纸盒个数的比值;
(3)拓展延伸:现在仓库里有张正方形纸板和张长方形纸板,如果做两种纸盒若干个,恰好使库存的纸板用完,则的值可能是( )
A.2013 B.2014 C.2015 D.2016
19.某校八年级(1)班名学生某次数学测验的成绩统计如表:
成绩分
人数人
(1)若这名学生成绩的平均数为分,求和的值.
(2)在(1)的条件下,求这名学生本次测验成绩的众数和中位数.
20.“预防为主,生命至上”.商场计划购进一批消防器材进行销售,已知购进15个干粉灭火器和20个消防自救呼吸器共需1500元,购进20个干粉灭火器和25个消防自救呼吸器共需1950元.
(1)求一个干粉灭火器和一个消防自救呼吸器的进价分别是多少元;
(2)该商场计划用4800元购进干粉灭火器和消防自救呼吸器共100个,销售时,干粉灭火器在进价的基础上加价进行销售;消防自救呼吸器每件加价10元进行销售,求全部售出后共可获利多少元.
21.对下面的问题,列出二元一次方程组,并根据问题的实际意义,找出问题的解.
(1)某村乡村振兴项目计划把黄桃加工成罐头,刚开始每天加工,后在技术顾问的指导下改进加工方法,每天加工,前后共用8天完成全部加工任务.这个项目改进加工方法前、后各用了多少天?
(2)在篮球联赛中,每场比赛都要分出胜负,每队胜1场得2分,负1场得1分.某队在10场比赛中得到16分,这个队的胜、负场数分别是多少?
22.为了节能减排,一家工厂将照明灯换成了节能灯.A车间购买了3盏甲型节能灯和5盏乙型节能灯,共花费50元;B车间购买了12盏甲型节能灯和4盏乙型节能灯,共花费88元.1盏甲型节能灯和1盏乙型节能灯的售价各是多少元?
23.七年级书法兴趣小组到文具店购买A,B两种型号的毛笔,文具店的销售方式是:
(1)一次性购买A型毛笔不超过20支时,按零售价销售;超过20支时,超过部分每支的价格比零售价低元.
(2)一次性购买B型毛笔不超过15支时,按零售价销售;超过15支时,超过部分每支的价格比零售价低元.
这个小组共有20名同学,若每人买1支A型毛笔和2支B型毛笔,共需支付325元;若每人买2支A型毛笔和1支B型毛笔,共需支付309元.这家文具店A,B型毛笔的零售价分别是多少?
24.快递公司为提高快递分拣的速度,决定购买机器人来代替人工分拣.已知购买甲型机器人1台,乙型机器人2台,共需7万元;购买甲型机器人2台,乙型机器人3台,共需12万元.
(1)甲,乙两种型号机器人的单价各为多少万元?
(2)已知1台甲型和1台乙型机器人每小时分拣快递的数量分别是1400件和1200件,该公司计划最多用16万元购买6台这两种型号的机器人,且至少购买甲型机器人2台,如何购买才能使每小时的分拣量最大?
《5.3二元一次方程组的应用》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A A D B B C B C B A
题号 11 12
答案 C A
1.A
【分析】本题考查了二元一次方程组的应用,解题关键是准确把握题目中的数量关系,找到等量关系列出方程组.
【详解】解:设文具盒单价为x元,钢笔单价为y元,
根据购买15 个文具盒和12支钢笔价格一样可列出方程;
根据在上述基础上少购买2个文具盒,多购买2支钢笔,则购买文具盒比钢笔少花36元可列出方程,
符合题意的方程组为,
故选:A.
2.A
【分析】本题考查二元一次方程组的实际应用,解题的关键是明确题意,找出等量关系,列出相应的二元一次方程组.
根据“一根绳子去量一根木条,绳子剩余4.5尺”可知:绳子=木条+4.5,再根据“将绳子对折再量木条,木条剩余1尺”可知:绳子=木条,据此列出二元一次方程组即可.
【详解】解:设木条长x尺,绳子长y尺,
那么可列方程组为:
,
故选:A.
3.D
【分析】解:设小明9:00看到的两位数,十位数为x,个位数为y,根据车的速度不变和12:00时看到的两位数字之和为6,即可列出二元一次方程组,解方程组即可求解.
【详解】解:设小明9:00看到的两位数,十位数为x,个位数为y,由题意列方程组得:,
解得:,
∴9:00时看到的两位数是15.
10:00时看到里程碑上的数是
故选:D
【点睛】本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题关键.
4.B
【分析】根据等量关系人出半,盈四;人出少半,不足三列方程组即可.
【详解】解:由题意知,可列方程为:
故选B.
【点睛】本题考查了二元一次方程组的应用.解题的关键在于理解题意.
5.B
【分析】根据题意可得等量关系:①去年的收入为元去年的支出元结余5000元;②今年的收入今年的支出今年可节余9500元,根据等量关系列出方程组即可.
【详解】解:设去年的收入为元,支出为元,根据题意可得:
,
故选:B.
【点睛】本题考查了由实际问题抽象出二元一次方程组,根据实际问题中的条件列方程组时,要注意抓住题目中的一些关键性词语,找出等量关系,列出方程组,找到两个等量关系是解决本题的关键.
6.C
【分析】根据“小兰去市场买了36米布”、“1只玩偶兔子和2个福袋配成一套礼物”即可列出二元一次方程组.
【详解】解:∵“小兰去市场买了36米布”
∴
∵“1只玩偶兔子和2个福袋配成一套礼物”
∴福袋的数量是玩偶兔子数量的2倍
∴
故:
故选:C
【点睛】本题考查配套问题.注意1只玩偶兔子和2个福袋配成一套礼物=福袋的数量是玩偶兔子数量的2倍.
7.B
【分析】设每辆大货车一次可运货x吨,每辆小货车一次可运货y吨,根据2辆大货车与3辆小货车一次共可运货15.5吨,5辆大货车与6辆小货车一次共可运货35吨,即可得出关于x,y的二元一次方程组,解之即可得出结论.
【详解】解:设每辆大货车一次可运货x吨,每辆小货车一次可运货y吨,依题意得:
,
解得:
.
故选:B.
【点睛】本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.
8.C
【分析】本题考查了二元一次方程组的实际应用,解题关键是找准等量关系.
设安排x个工人生产螺杆,y个工人生产螺母,根据“生产线现有个工人”、“现在要求工人每天生产的螺杆和螺母完整配套而没有剩余”列出方程组即可.
【详解】解:设安排x个工人生产螺杆,y个工人生产螺母,
根据题意得:,
故选:C.
9.B
【分析】本题考查了二元一次方程组在行程问题中的应用,等量关系式:列车小时行驶的路程站与站的距离千米,列车小时行驶的路程站与站的距离千米,据此列出方程组,即可求解;找出等量关系式是解题的关键.
【详解】解:设火车的速度为千米/小时,站与站相距千米,由题意得
,
解得:,
(小时),
故答案:B.
10.A
【分析】设原来的两个加数分别为和,小明将后多写一个0,即x扩大10倍,得到;小亮将后多写一个0即y扩大10倍,得到,解方程组即可.
本题考查了方程组的应用,熟练掌握解方程组是解题的关键.
【详解】解:设原来的两个加数分别为和,
根据题意,得,
解得.
故选:A.
11.C
【分析】本题考查了二元一次方程组的应用,设原来笔袋中黑色中性笔有支,红色中性笔有支,根据“从中随机取出一支笔,取出的是黑色中性笔的概率,如果再往笔袋中放进6支红色中性笔,这时从中随机取出一支笔是黑色中性笔的概率变为”列出方程组,解方程即可得出答案.
【详解】解:设原来笔袋中黑色中性笔有支,红色中性笔有支,
由题意得:,
整理得:,
解得,
原来笔袋中黑色中性笔有支,
故选:C.
12.A
【分析】此题考查了二元一次方程组的实际应用,长方形的性质,根据长方形的两组对边分别相等列出方程组是解题的关键.
设一块长方形墙砖的长为,宽为,然后用的代数式分别表示出长方形的长为,两条宽分别为,,进而根据长方形的性质列出方程组,解方程组得到的值,再根据长方形面积计算公式即可求出面积,
【详解】解:设一块长方形墙砖的长为,宽为,依题意得,
,
解得,
∴每一块长方形墙砖的面积为:
答:每一块长方形墙砖的面积为.
故选:A.
13.
【分析】本题考查了代数式求值,解二元一次方程组.由,,可知每一横行、每一竖列以及对角线上的数字之和都是0,如图1,由,解得,,解得,,解得,,解得,,解得,如图2,由题意知,,整理得,,,整理得,,联立,解得,然后求解即可.
【详解】解:∵,
∴,即每一横行、每一竖列以及对角线上的数字之和都是0,
如图1,
a 2
m b c
d e n
∵,解得,
∵,解得,
∵,解得,
∵,解得,
∵,解得,
如图2,
1 2
m
n
由题意知,,整理得,,
,整理得,,
∴,
解得,
∴,
故答案为:.
14.
【分析】设三角形的外心为,然后根据外心的性质可以得到关于x、y的方程组,解方程组即可得解.
【详解】解:设三角形的外心为,由题意可得:
,
则,
解方程可得:,
故答案为.
【点睛】本题考查圆的综合应用,熟练掌握三角形外接圆的性质、二元一次方程组的解法是解题关键.
15.33.5
【分析】本题考查二元一次方程组的应用,正确理解题意,寻找等量关系是解题的关键;
设甲种货车可运输货物,乙种货车可运输货物,根据表格中所提供的信息列二元一次方程组,
求出两种货车每次的载重吨数,再根据题中所给数据列式计算即可.
【详解】解:设甲种货车可运输货物,乙种货车可运输货物,
由题知,,
解方程组得
用4辆甲种货车和7辆乙种货车可运输货物.
故答案为:33.5.
16.
【分析】本题考查了二元一次方程组的应用.
设新轮胎安装在后轮行驶时更换到前轮,在前轮又行驶了报废,根据通过交换前后轮轮胎使一辆自行车的一对新轮胎同时报废,可列出关于x,y的二元一次方程组,解之可得出x,y的值,再将其代入中,即可求出结论.
【详解】解:设新轮胎安装在后轮行驶时更换到前轮,在前轮又行驶了报废,
根据题意得:,
解得:,
∴(),
∴这对新轮胎一共能支持自行车行驶.
故答案为:.
17.
【分析】本题考查了二元一次方程组的应用,设节火车车厢装吨化肥,辆汽车装吨化肥,根据运输吨化肥,装载了节火车车厢和辆汽车;运输吨化肥,袋载了节火车车厢和辆汽车,可列方程组,把方程组中的两个方程相加可得:,所以可得节火车车厢和辆汽车共装吨化肥.
【详解】解:设节火车车厢装吨化肥,辆汽车装吨化肥,
根据题意可得:,
得:,
方程两边同时除以得:,
节火车车厢和辆汽车共装吨化肥.
故答案为:.
18.(1)①第二次,见解析;②做成40个竖式纸盒,260个横式纸盒
(2)3
(3)C
【分析】本题考查了二元一次方程组的应用,理解题意,找到正确的数量关系是本题的关键.
(1)①设做成x个竖式纸盒,y个横式纸盒,由领取的正方形的纸板和长方形的纸板之和应该是5的倍数,可判断第二次记录错误;
②由第一次记录,列出方程组,可求解;
(2)由正方形纸板数与长方形纸板数之比为1:3,可得,可求解;
(3)设做竖式和横式的两种无盖纸盒分别为x个、y个,然后根据所需长方形纸板和正方形纸板的张数列出方程组,再根据x、y的系数表示出并判断为5的倍数,然后选择答案即可.
【详解】(1)解:①第二次记录错误,
理由如下:设做成x个竖式纸盒,y个横式纸盒,
则需要正方形纸板张,需要长方形的纸板张,
∴领取的正方形的纸板和长方形的纸板之和为,应该是5的倍数,
而,,1422不能被5整除,
∴第二次记录有误;
②由题意可得:,
解得:,
答:做成40个竖式纸盒,260个横式纸盒;
(2)解:由题意可得:,
解得:,
∴,
答:竖式纸盒与横式纸盒个数的比值为3.
(3)解:设做竖式和横式的两种无盖纸盒分别为x个、y个,
根据题意得:,
两式相加得,,
∵x、y都是正整数,
∴是5的倍数,
∵2013、2014、2015、2016四个数中只有2015是5的倍数,
∴的值可能是2015.
故选:C.
19.(1)5;7;
(2)90;80
【分析】(1)根据题意可以得到关于x、y的二元一次方程组,解方程组即可求得x、y的值;
(2)根据众数和中位数的定义求出答案即可.
【详解】(1)解:由题意得:,
解得:,
∴x的值为5,y的值为7;
(2)解:由(1)得,分的人数最多,故众数为分,
中位数为从低到高第和第位同学成绩的平均值为分,
∴众数为,中位数为.
【点睛】本题考查了平均数、众数与中位数的知识以及解二元一次方程组,掌握各知识点的概念及方法是解答本题的关键.
20.(1)一个干粉灭火器的进价为60元,一个消防自救呼吸器的进价为30元
(2)全部售出后共可获利1480元
【分析】本题考查了二元一次方程组的应用,理解题意找准等量关系列出方程是解题的关键.
(1)设一个干粉灭火器的进价为元,一个消防自救呼吸器的进价为元,根据题意列出方程组,解出的值即可解答;
(2)设购进干粉灭火器个,购进消防自救呼吸器个,根据题意列出方程组,解出的值,再计算获利即可解答.
【详解】(1)解:设一个干粉灭火器的进价为元,一个消防自救呼吸器的进价为元,
由题意得,,
解得:,
答:一个干粉灭火器的进价为60元,一个消防自救呼吸器的进价为30元.
(2)解:设购进干粉灭火器个,购进消防自救呼吸器个,
由题意得,,
解得:,
购进干粉灭火器60个,购进消防自救呼吸器40个,
全部售出后共可获利(元),
答:全部售出后共可获利1480元.
21.(1)这个项目改进加工方法前、后各用了2天、6天.
(2)这个队的胜、负场数分别是6场和4场.
【分析】本题主要考查了二元一次方程组的应用,审清题意、正确列出二元一次方程组成为解题的关键.
(1)设这个项目改进加工方法前、后各用了x、y天,然后根据题意列二元一次方程组求解即可;
(2)设这个队的胜、负场数分别是m、n场,然后根据题意列二元一次方程组求解即可.
【详解】(1)解:设这个项目改进加工方法前、后各用了x天和y天,
由题意可得:,解得:.
答:这个项目改进加工方法前、后各用了2天和6天.
(2)解:设这个队的胜、负场数分别是m场和n场,
由题意可得:,解得:.
答:这个队的胜、负场数分别是6场和4场.
22.1盏甲型节能灯售价为5元,1盏乙型节能灯的售价为7元
【分析】本题考查了二元一次方程解决实际问题,正确列出二元一次方程是解题的关键.
设出两种型号的节能灯的价格,然后算出各自花费的金额,其和等于54元,可列出方程求解.
【详解】解:设1盏甲型节能灯售价为x元,1盏乙型节能灯的售价为y元,根据题意得:
,
解得,
答:1盏甲型节能灯售价为5元,1盏乙型节能灯的售价为7元.
23.这家文具店A型毛笔的零售价为5元,B型毛笔的零售价为6元
【分析】设这家文具店A型毛笔的零售价为元,B型毛笔的零售价为元,
根据题意列出方程组解答即可.
本题考查了方程组的应用,正确列出方程组是解题的关键.
【详解】解:设这家文具店A型毛笔的零售价为元,B型毛笔的零售价为元,
根据题意得:
,
解得,
答:这家文具店A型毛笔的零售价为5元,B型毛笔的零售价为6元.
24.(1)甲型机器人的单价是3万元,乙型机器人的单价是2万元
(2)购进甲型机器人4台,乙型机器人2台时,分拣量最大
【分析】(1)设甲型机器人的单价是x万元,乙型机器人的单价是y万元,根据“购买甲型机器人1台,乙型机器人2台,共需7万元;购买甲型机器人2台,乙型机器人3台,共需12万元”,即可得出关于x,y的二元一次方程组,解之即可得出结论.
(2)设购买甲型机器人m台,则购买乙型机器人台,根据“该公司计划最多用16万元购买6台这两种型号的机器人,且至少购买甲型机器人2台”,即可得出关于m的一元一次不等式组,解之即可得出m的取值范围,设6台机器人每小时的分拣量为w,利用总分拣量=每台机器人的分拣量×购买该型机器人的数量,即可得出w关于m的函数关系式,再利用一次函数的性质,即可解决最值问题.
【详解】(1)解:设甲型机器人的单价是x万元,乙型机器人的单价是y万元,
依题意,得
解得
答:甲型机器人的单价是3万元,乙型机器人的单价是2万元.
(2)解:设购买甲型机器人m台,则购买乙型机器人台.
依题意,得,
解得.
设6台机器人每小时的分拣量为w,则.
∵,
∴w随m的增大而增大,
∴当时,w取得最大值,此时,
∴购买甲型机器人4台,乙型机器人2台时,才能使每小时的分拣量最大.
【点睛】本题考查了二元一次方程组的应用、一元一次不等式组的应用以及一次函数的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)根据各数量之间的关系,找出w关于m的函数关系式.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
5.3二元一次方程组的应用
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.为奖励在“缤纷节”汇演中表现突出的同学,班主任派小王到文具店为获奖同学购买奖品. 小王发现,购买15 个文具盒和12支钢笔价格一样;如果在上述基础上少购买2个文具盒,多购买2支钢笔,则购买文具盒比钢笔少花36元. 设文具盒单价为x元,钢笔单价为y元,则符合题意的方程组为( )
A. B.
C. D.
2.我国古代数学古典名著《孙子算经》中记载:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”其大意是:用一根绳子去量一根木条,绳子还剩余4.5尺;将绳子对折再量,木条还剩余1尺;问木条多少尺?如果设木条长为尺,绳子长为尺,则下面所列方程组正确的是( )
A. B. C. D.
3.爸爸骑摩托车带着小明在公路上匀速行驶,小明每隔一段时间看到的里程碑上的数如下:
时刻 9:00 10:00 11:30
里程碑上的数 是一个两位数,它的两个数字之和是6 是一个两位数,它的十位与个位数字与9:00所看到的正好互换了 是一个三位数,它比9:00时看到的两位数中间多了个0
则10:00时看到里程碑上的数是( )
A.15 B.24 C.42 D.51
4.我国古代数学名著《九章算术》中记载:“今有共买琎,人出半,盈四;人出少半,不足三.问人数、琎价各几何?”意思是:一起去买琎(一种像玉的石头),每个人出两,则多4两;每个人出两,则不足3两.问人数、琎的价格分别是多少?如果设人数x人,琎的价格为y两,那么可列成的方程组为( )
A. B. C. D.
5.小李家去年节余5000元,今年可节余9500元,并且今年收入比去年高,支出比去年低,今年的收入与支出各是多少?设去年的收入为元,支出为元,则可列方程组为( )
A. B. C. D.
6.兔年来临,小兰要做玩偶兔子和福袋作为新年礼物,她去市场买了36米布,每米布可以做兔子25只,或者福袋40个,小兰将1只玩偶兔子和2个福袋配成一套礼物,结果发现布没有剩余,恰好配套做成了礼物.若设用x米布做兔子,用y米布做福袋,则可列出方程组为( )
A. B. C. D.
7.有大小两种货车,2辆大货车与3辆小货车一次共可运货15.5吨,5辆大货车与6辆小货车一次共可运货35吨,则每辆小货车一次可运货( )
A.2吨 B.2.5吨 C.3吨 D.3.5吨
8.某生产线现有个工人,一个工人每天可生产6个螺杆或个螺母,1个螺杆和2个螺母为一套,现在要求工人每天生产的螺杆和螺母完整配套而没有剩余,若设安排x个工人生产螺杆,y个工人生产螺母,则列出正确的二元一次方程组为( )
A. B.
C. D.
9.一条铁路线A,B,C三个车站的位置如图所示,已知B,C两车站之间相距500千米.火车从B站出发,向C站方向行驶,经过30分钟,距A站130千米;经过2小时,距A站280千米.火车从B站开出多少时间后可到达C站?( )
A.4小时 B.5小时 C.6小时 D.7小时
10.小明和小亮做加法游戏,小明在一个加数后面多写了一个0,得到的和为242;而小亮在另一个加数后面多写了一个0,得到的和为341,原来的两个加数分别是( )
A.21,32 B.12,23 C.31,22 D.41,42
11.某同学的笔袋中有若干支黑色中性笔和红色中性笔(除笔芯颜色不同外,其他都相同),从中随机取出一支笔,取出的是黑色中性笔的概率,如果再往笔袋中放进6支红色中性笔,这时从中随机取出一支笔是黑色中性笔的概率变为,则笔袋中的黑色中性笔有( ).
A.8支 B.6支 C.4支 D.2支
12.如图,王英家客厅的电视背景墙是由8块形状大小相同的长方形墙砖砌成,已知电视背景墙的长度为,则每一块长方形墙砖的面积为( )
A. B. C. D.
二、填空题
13.幻方是古老的数学问题,我国古代的《洛书》中记载了最早的幻方——九宫图.将数字,,,,0,1,2,3,4分别填入如图所示的幻方中,要求每一横行、每一竖列以及对角线上的数字之和都是同一个值,则的值是 .
2
m
n
14.如图,△ABC的三个顶点都在直角坐标系中的格点上,图中△ABC外接圆的圆心坐标是 .
15.某公司要将一批货物运往某地,打算租用甲、乙两种货车,以前租用这两种货车的信息如下表:
第一次 第二次
甲种货车的辆数 2 5
乙种货车的辆数 3 6
累计运货量/t 15.5 35
现打算租用4辆甲种货车和7辆乙种货车,可一次刚好运完这批货物,则这批货物共有 t.
16.一辆自行车换胎,若新轮胎安装在前轮,则自行车行驶2500后报废;若新轮胎安装在后轮,则自行车行驶1500后报废,如果可以在自行车行驶一定的路程后,通过交换前后轮轮胎使一辆自行车的一对新轮胎同时报废,那么这对新轮胎一共能支持自行车行驶 .
17.运输吨化肥,装载了节火车车厢和辆汽车;运输吨化肥,袋载了节火车车厢和辆汽车,则节火车车厢和辆汽车共装 吨化肥.
三、解答题
18.工作人员从仓库领取如图1中的长方形和正方形纸板作侧面和底面,做成如图2的竖式和横式的两种无盖纸盒若干个,恰好使领取的纸板用完.
(1)下表是工作人员两次领取纸板数的记录:
次数 正方形纸板(张) 长方形纸板(张)
第一次 560 940
第二次 420 1002
①仓库管理员在核查时,发现一次记录有误,请判断第几次的记录有误,并说明理由;
②记录正确的那一次,利用领取的纸板做了竖式和横式纸盒各多少个?
(2)若工作人员某次领取的正方形纸板数与长方形纸板数之比为1:3,请你求出利用这些纸板做出的竖式纸盒与横式纸盒个数的比值;
(3)拓展延伸:现在仓库里有张正方形纸板和张长方形纸板,如果做两种纸盒若干个,恰好使库存的纸板用完,则的值可能是( )
A.2013 B.2014 C.2015 D.2016
19.某校八年级(1)班名学生某次数学测验的成绩统计如表:
成绩分
人数人
(1)若这名学生成绩的平均数为分,求和的值.
(2)在(1)的条件下,求这名学生本次测验成绩的众数和中位数.
20.“预防为主,生命至上”.商场计划购进一批消防器材进行销售,已知购进15个干粉灭火器和20个消防自救呼吸器共需1500元,购进20个干粉灭火器和25个消防自救呼吸器共需1950元.
(1)求一个干粉灭火器和一个消防自救呼吸器的进价分别是多少元;
(2)该商场计划用4800元购进干粉灭火器和消防自救呼吸器共100个,销售时,干粉灭火器在进价的基础上加价进行销售;消防自救呼吸器每件加价10元进行销售,求全部售出后共可获利多少元.
21.对下面的问题,列出二元一次方程组,并根据问题的实际意义,找出问题的解.
(1)某村乡村振兴项目计划把黄桃加工成罐头,刚开始每天加工,后在技术顾问的指导下改进加工方法,每天加工,前后共用8天完成全部加工任务.这个项目改进加工方法前、后各用了多少天?
(2)在篮球联赛中,每场比赛都要分出胜负,每队胜1场得2分,负1场得1分.某队在10场比赛中得到16分,这个队的胜、负场数分别是多少?
22.为了节能减排,一家工厂将照明灯换成了节能灯.A车间购买了3盏甲型节能灯和5盏乙型节能灯,共花费50元;B车间购买了12盏甲型节能灯和4盏乙型节能灯,共花费88元.1盏甲型节能灯和1盏乙型节能灯的售价各是多少元?
23.七年级书法兴趣小组到文具店购买A,B两种型号的毛笔,文具店的销售方式是:
(1)一次性购买A型毛笔不超过20支时,按零售价销售;超过20支时,超过部分每支的价格比零售价低元.
(2)一次性购买B型毛笔不超过15支时,按零售价销售;超过15支时,超过部分每支的价格比零售价低元.
这个小组共有20名同学,若每人买1支A型毛笔和2支B型毛笔,共需支付325元;若每人买2支A型毛笔和1支B型毛笔,共需支付309元.这家文具店A,B型毛笔的零售价分别是多少?
24.快递公司为提高快递分拣的速度,决定购买机器人来代替人工分拣.已知购买甲型机器人1台,乙型机器人2台,共需7万元;购买甲型机器人2台,乙型机器人3台,共需12万元.
(1)甲,乙两种型号机器人的单价各为多少万元?
(2)已知1台甲型和1台乙型机器人每小时分拣快递的数量分别是1400件和1200件,该公司计划最多用16万元购买6台这两种型号的机器人,且至少购买甲型机器人2台,如何购买才能使每小时的分拣量最大?
《5.3二元一次方程组的应用》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A A D B B C B C B A
题号 11 12
答案 C A
1.A
【分析】本题考查了二元一次方程组的应用,解题关键是准确把握题目中的数量关系,找到等量关系列出方程组.
【详解】解:设文具盒单价为x元,钢笔单价为y元,
根据购买15 个文具盒和12支钢笔价格一样可列出方程;
根据在上述基础上少购买2个文具盒,多购买2支钢笔,则购买文具盒比钢笔少花36元可列出方程,
符合题意的方程组为,
故选:A.
2.A
【分析】本题考查二元一次方程组的实际应用,解题的关键是明确题意,找出等量关系,列出相应的二元一次方程组.
根据“一根绳子去量一根木条,绳子剩余4.5尺”可知:绳子=木条+4.5,再根据“将绳子对折再量木条,木条剩余1尺”可知:绳子=木条,据此列出二元一次方程组即可.
【详解】解:设木条长x尺,绳子长y尺,
那么可列方程组为:
,
故选:A.
3.D
【分析】解:设小明9:00看到的两位数,十位数为x,个位数为y,根据车的速度不变和12:00时看到的两位数字之和为6,即可列出二元一次方程组,解方程组即可求解.
【详解】解:设小明9:00看到的两位数,十位数为x,个位数为y,由题意列方程组得:,
解得:,
∴9:00时看到的两位数是15.
10:00时看到里程碑上的数是
故选:D
【点睛】本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题关键.
4.B
【分析】根据等量关系人出半,盈四;人出少半,不足三列方程组即可.
【详解】解:由题意知,可列方程为:
故选B.
【点睛】本题考查了二元一次方程组的应用.解题的关键在于理解题意.
5.B
【分析】根据题意可得等量关系:①去年的收入为元去年的支出元结余5000元;②今年的收入今年的支出今年可节余9500元,根据等量关系列出方程组即可.
【详解】解:设去年的收入为元,支出为元,根据题意可得:
,
故选:B.
【点睛】本题考查了由实际问题抽象出二元一次方程组,根据实际问题中的条件列方程组时,要注意抓住题目中的一些关键性词语,找出等量关系,列出方程组,找到两个等量关系是解决本题的关键.
6.C
【分析】根据“小兰去市场买了36米布”、“1只玩偶兔子和2个福袋配成一套礼物”即可列出二元一次方程组.
【详解】解:∵“小兰去市场买了36米布”
∴
∵“1只玩偶兔子和2个福袋配成一套礼物”
∴福袋的数量是玩偶兔子数量的2倍
∴
故:
故选:C
【点睛】本题考查配套问题.注意1只玩偶兔子和2个福袋配成一套礼物=福袋的数量是玩偶兔子数量的2倍.
7.B
【分析】设每辆大货车一次可运货x吨,每辆小货车一次可运货y吨,根据2辆大货车与3辆小货车一次共可运货15.5吨,5辆大货车与6辆小货车一次共可运货35吨,即可得出关于x,y的二元一次方程组,解之即可得出结论.
【详解】解:设每辆大货车一次可运货x吨,每辆小货车一次可运货y吨,依题意得:
,
解得:
.
故选:B.
【点睛】本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.
8.C
【分析】本题考查了二元一次方程组的实际应用,解题关键是找准等量关系.
设安排x个工人生产螺杆,y个工人生产螺母,根据“生产线现有个工人”、“现在要求工人每天生产的螺杆和螺母完整配套而没有剩余”列出方程组即可.
【详解】解:设安排x个工人生产螺杆,y个工人生产螺母,
根据题意得:,
故选:C.
9.B
【分析】本题考查了二元一次方程组在行程问题中的应用,等量关系式:列车小时行驶的路程站与站的距离千米,列车小时行驶的路程站与站的距离千米,据此列出方程组,即可求解;找出等量关系式是解题的关键.
【详解】解:设火车的速度为千米/小时,站与站相距千米,由题意得
,
解得:,
(小时),
故答案:B.
10.A
【分析】设原来的两个加数分别为和,小明将后多写一个0,即x扩大10倍,得到;小亮将后多写一个0即y扩大10倍,得到,解方程组即可.
本题考查了方程组的应用,熟练掌握解方程组是解题的关键.
【详解】解:设原来的两个加数分别为和,
根据题意,得,
解得.
故选:A.
11.C
【分析】本题考查了二元一次方程组的应用,设原来笔袋中黑色中性笔有支,红色中性笔有支,根据“从中随机取出一支笔,取出的是黑色中性笔的概率,如果再往笔袋中放进6支红色中性笔,这时从中随机取出一支笔是黑色中性笔的概率变为”列出方程组,解方程即可得出答案.
【详解】解:设原来笔袋中黑色中性笔有支,红色中性笔有支,
由题意得:,
整理得:,
解得,
原来笔袋中黑色中性笔有支,
故选:C.
12.A
【分析】此题考查了二元一次方程组的实际应用,长方形的性质,根据长方形的两组对边分别相等列出方程组是解题的关键.
设一块长方形墙砖的长为,宽为,然后用的代数式分别表示出长方形的长为,两条宽分别为,,进而根据长方形的性质列出方程组,解方程组得到的值,再根据长方形面积计算公式即可求出面积,
【详解】解:设一块长方形墙砖的长为,宽为,依题意得,
,
解得,
∴每一块长方形墙砖的面积为:
答:每一块长方形墙砖的面积为.
故选:A.
13.
【分析】本题考查了代数式求值,解二元一次方程组.由,,可知每一横行、每一竖列以及对角线上的数字之和都是0,如图1,由,解得,,解得,,解得,,解得,,解得,如图2,由题意知,,整理得,,,整理得,,联立,解得,然后求解即可.
【详解】解:∵,
∴,即每一横行、每一竖列以及对角线上的数字之和都是0,
如图1,
a 2
m b c
d e n
∵,解得,
∵,解得,
∵,解得,
∵,解得,
∵,解得,
如图2,
1 2
m
n
由题意知,,整理得,,
,整理得,,
∴,
解得,
∴,
故答案为:.
14.
【分析】设三角形的外心为,然后根据外心的性质可以得到关于x、y的方程组,解方程组即可得解.
【详解】解:设三角形的外心为,由题意可得:
,
则,
解方程可得:,
故答案为.
【点睛】本题考查圆的综合应用,熟练掌握三角形外接圆的性质、二元一次方程组的解法是解题关键.
15.33.5
【分析】本题考查二元一次方程组的应用,正确理解题意,寻找等量关系是解题的关键;
设甲种货车可运输货物,乙种货车可运输货物,根据表格中所提供的信息列二元一次方程组,
求出两种货车每次的载重吨数,再根据题中所给数据列式计算即可.
【详解】解:设甲种货车可运输货物,乙种货车可运输货物,
由题知,,
解方程组得
用4辆甲种货车和7辆乙种货车可运输货物.
故答案为:33.5.
16.
【分析】本题考查了二元一次方程组的应用.
设新轮胎安装在后轮行驶时更换到前轮,在前轮又行驶了报废,根据通过交换前后轮轮胎使一辆自行车的一对新轮胎同时报废,可列出关于x,y的二元一次方程组,解之可得出x,y的值,再将其代入中,即可求出结论.
【详解】解:设新轮胎安装在后轮行驶时更换到前轮,在前轮又行驶了报废,
根据题意得:,
解得:,
∴(),
∴这对新轮胎一共能支持自行车行驶.
故答案为:.
17.
【分析】本题考查了二元一次方程组的应用,设节火车车厢装吨化肥,辆汽车装吨化肥,根据运输吨化肥,装载了节火车车厢和辆汽车;运输吨化肥,袋载了节火车车厢和辆汽车,可列方程组,把方程组中的两个方程相加可得:,所以可得节火车车厢和辆汽车共装吨化肥.
【详解】解:设节火车车厢装吨化肥,辆汽车装吨化肥,
根据题意可得:,
得:,
方程两边同时除以得:,
节火车车厢和辆汽车共装吨化肥.
故答案为:.
18.(1)①第二次,见解析;②做成40个竖式纸盒,260个横式纸盒
(2)3
(3)C
【分析】本题考查了二元一次方程组的应用,理解题意,找到正确的数量关系是本题的关键.
(1)①设做成x个竖式纸盒,y个横式纸盒,由领取的正方形的纸板和长方形的纸板之和应该是5的倍数,可判断第二次记录错误;
②由第一次记录,列出方程组,可求解;
(2)由正方形纸板数与长方形纸板数之比为1:3,可得,可求解;
(3)设做竖式和横式的两种无盖纸盒分别为x个、y个,然后根据所需长方形纸板和正方形纸板的张数列出方程组,再根据x、y的系数表示出并判断为5的倍数,然后选择答案即可.
【详解】(1)解:①第二次记录错误,
理由如下:设做成x个竖式纸盒,y个横式纸盒,
则需要正方形纸板张,需要长方形的纸板张,
∴领取的正方形的纸板和长方形的纸板之和为,应该是5的倍数,
而,,1422不能被5整除,
∴第二次记录有误;
②由题意可得:,
解得:,
答:做成40个竖式纸盒,260个横式纸盒;
(2)解:由题意可得:,
解得:,
∴,
答:竖式纸盒与横式纸盒个数的比值为3.
(3)解:设做竖式和横式的两种无盖纸盒分别为x个、y个,
根据题意得:,
两式相加得,,
∵x、y都是正整数,
∴是5的倍数,
∵2013、2014、2015、2016四个数中只有2015是5的倍数,
∴的值可能是2015.
故选:C.
19.(1)5;7;
(2)90;80
【分析】(1)根据题意可以得到关于x、y的二元一次方程组,解方程组即可求得x、y的值;
(2)根据众数和中位数的定义求出答案即可.
【详解】(1)解:由题意得:,
解得:,
∴x的值为5,y的值为7;
(2)解:由(1)得,分的人数最多,故众数为分,
中位数为从低到高第和第位同学成绩的平均值为分,
∴众数为,中位数为.
【点睛】本题考查了平均数、众数与中位数的知识以及解二元一次方程组,掌握各知识点的概念及方法是解答本题的关键.
20.(1)一个干粉灭火器的进价为60元,一个消防自救呼吸器的进价为30元
(2)全部售出后共可获利1480元
【分析】本题考查了二元一次方程组的应用,理解题意找准等量关系列出方程是解题的关键.
(1)设一个干粉灭火器的进价为元,一个消防自救呼吸器的进价为元,根据题意列出方程组,解出的值即可解答;
(2)设购进干粉灭火器个,购进消防自救呼吸器个,根据题意列出方程组,解出的值,再计算获利即可解答.
【详解】(1)解:设一个干粉灭火器的进价为元,一个消防自救呼吸器的进价为元,
由题意得,,
解得:,
答:一个干粉灭火器的进价为60元,一个消防自救呼吸器的进价为30元.
(2)解:设购进干粉灭火器个,购进消防自救呼吸器个,
由题意得,,
解得:,
购进干粉灭火器60个,购进消防自救呼吸器40个,
全部售出后共可获利(元),
答:全部售出后共可获利1480元.
21.(1)这个项目改进加工方法前、后各用了2天、6天.
(2)这个队的胜、负场数分别是6场和4场.
【分析】本题主要考查了二元一次方程组的应用,审清题意、正确列出二元一次方程组成为解题的关键.
(1)设这个项目改进加工方法前、后各用了x、y天,然后根据题意列二元一次方程组求解即可;
(2)设这个队的胜、负场数分别是m、n场,然后根据题意列二元一次方程组求解即可.
【详解】(1)解:设这个项目改进加工方法前、后各用了x天和y天,
由题意可得:,解得:.
答:这个项目改进加工方法前、后各用了2天和6天.
(2)解:设这个队的胜、负场数分别是m场和n场,
由题意可得:,解得:.
答:这个队的胜、负场数分别是6场和4场.
22.1盏甲型节能灯售价为5元,1盏乙型节能灯的售价为7元
【分析】本题考查了二元一次方程解决实际问题,正确列出二元一次方程是解题的关键.
设出两种型号的节能灯的价格,然后算出各自花费的金额,其和等于54元,可列出方程求解.
【详解】解:设1盏甲型节能灯售价为x元,1盏乙型节能灯的售价为y元,根据题意得:
,
解得,
答:1盏甲型节能灯售价为5元,1盏乙型节能灯的售价为7元.
23.这家文具店A型毛笔的零售价为5元,B型毛笔的零售价为6元
【分析】设这家文具店A型毛笔的零售价为元,B型毛笔的零售价为元,
根据题意列出方程组解答即可.
本题考查了方程组的应用,正确列出方程组是解题的关键.
【详解】解:设这家文具店A型毛笔的零售价为元,B型毛笔的零售价为元,
根据题意得:
,
解得,
答:这家文具店A型毛笔的零售价为5元,B型毛笔的零售价为6元.
24.(1)甲型机器人的单价是3万元,乙型机器人的单价是2万元
(2)购进甲型机器人4台,乙型机器人2台时,分拣量最大
【分析】(1)设甲型机器人的单价是x万元,乙型机器人的单价是y万元,根据“购买甲型机器人1台,乙型机器人2台,共需7万元;购买甲型机器人2台,乙型机器人3台,共需12万元”,即可得出关于x,y的二元一次方程组,解之即可得出结论.
(2)设购买甲型机器人m台,则购买乙型机器人台,根据“该公司计划最多用16万元购买6台这两种型号的机器人,且至少购买甲型机器人2台”,即可得出关于m的一元一次不等式组,解之即可得出m的取值范围,设6台机器人每小时的分拣量为w,利用总分拣量=每台机器人的分拣量×购买该型机器人的数量,即可得出w关于m的函数关系式,再利用一次函数的性质,即可解决最值问题.
【详解】(1)解:设甲型机器人的单价是x万元,乙型机器人的单价是y万元,
依题意,得
解得
答:甲型机器人的单价是3万元,乙型机器人的单价是2万元.
(2)解:设购买甲型机器人m台,则购买乙型机器人台.
依题意,得,
解得.
设6台机器人每小时的分拣量为w,则.
∵,
∴w随m的增大而增大,
∴当时,w取得最大值,此时,
∴购买甲型机器人4台,乙型机器人2台时,才能使每小时的分拣量最大.
【点睛】本题考查了二元一次方程组的应用、一元一次不等式组的应用以及一次函数的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)根据各数量之间的关系,找出w关于m的函数关系式.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
