第一章勾股定理同步练习(含解析)北师大版数学八年级上册
文档属性
| 名称 | 第一章勾股定理同步练习(含解析)北师大版数学八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 997.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-24 20:54:57 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第一章勾股定理
学校:___________姓名:___________班级:___________考号:___________
一、单选题
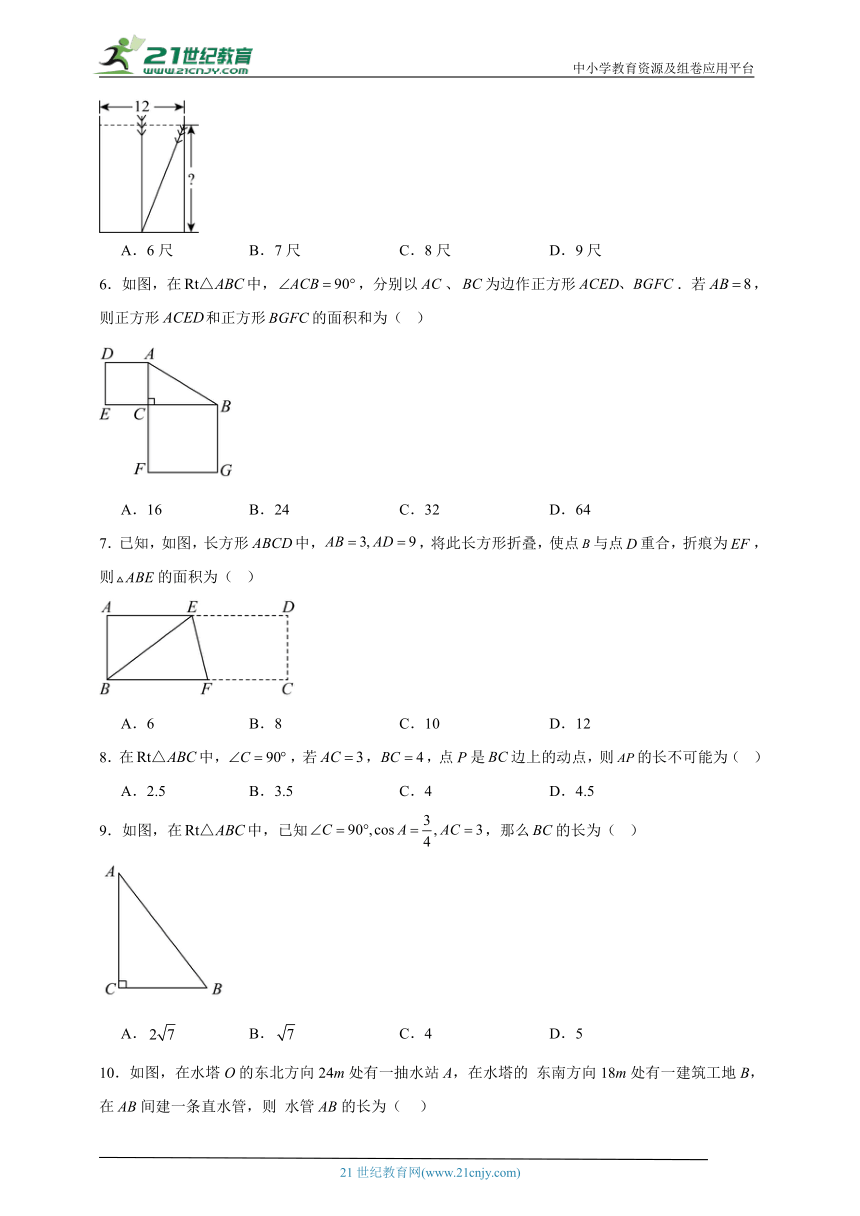
1.如图,将放在每个小正方形的边长为1的网格中,点,,均落在格点上,用一个圆面去覆盖,能够完全覆盖这个三角形的最小圆面的半径是( )
A.4 B. C. D.
2.池塘中有一朵荷花,它直立在水中,荷花高出水面半尺处长着一朵红莲,一阵风吹来把荷花吹倒在一边,红莲倒在水面位置距荷花生长处水平距离为2尺,则池塘深( )
A.3.75尺 B.3.25尺 C.4.25尺 D.3.5尺
3.如图,图中小正方形的边长都为1,的顶点都在格点上,则是( )
A.直角三角形 B.锐角三角形 C.钝角三角形 D.无法判断
4.下列四组数中,不是勾股数的是( )
A. B.
C. D.
5.我国古代数学著作《九章算术》中记载了一个问题:“今有池方一丈,葭()生其中,出水一尺.引葭赴岸,适与岸齐,问水深几何”(丈、尺都是长度单位,1丈尺.)其大意为:有一个水池,水面是一个边长为12尺的正方形,在水池中央有一根芦苇,它高出水面2尺.如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面.水的深度是多少?则水深为( )
A.6尺 B.7尺 C.8尺 D.9尺
6.如图,在中,,分别以、为边作正方形.若,则正方形和正方形的面积和为( )
A.16 B.24 C.32 D.64
7.已知,如图,长方形中,,将此长方形折叠,使点与点重合,折痕为,则的面积为( )
A.6 B.8 C.10 D.12
8.在中,,若,,点P是边上的动点,则的长不可能为( )
A.2.5 B.3.5 C.4 D.4.5
9.如图,在中,已知,那么的长为( )
A. B. C.4 D.5
10.如图,在水塔O的东北方向24m处有一抽水站A,在水塔的 东南方向18m处有一建筑工地B,在AB间建一条直水管,则 水管AB的长为( )
A.40m B.45m C.30m D.35m
11.一架长的梯子斜靠在墙上,梯子底端到墙的距离为.若梯子顶端下滑,那么梯子底端在水平方向上滑动了( )
A. B.小于 C.大于 D.无法确定
12.在学习勾股定理时,甲同学用两个相同的直角三角形和一个等腰三角形构成如图甲所示的直角梯形;乙同学用四个相同的直角三角形构成如图乙所示的大正方形,中间是一个小正方形,甲、乙两位同学给出的构图方案,可以证明勾股定理的是( )
A.甲 B.乙
C.甲,乙都可以 D.甲,乙都不可以
二、填空题
13.直角三角形的两直角边长为5和12,则该三角形的斜边长为 .
14.如图,对折矩形纸片ABCD,使AD和BC重合,得到折痕EF;把纸片展平再折,使点A落在EF上的点处,则 度,折叠后折痕为BM,BM与EF相交于点N,如果直线交CD于点O,,,则OD= .
15.中,,,则 .
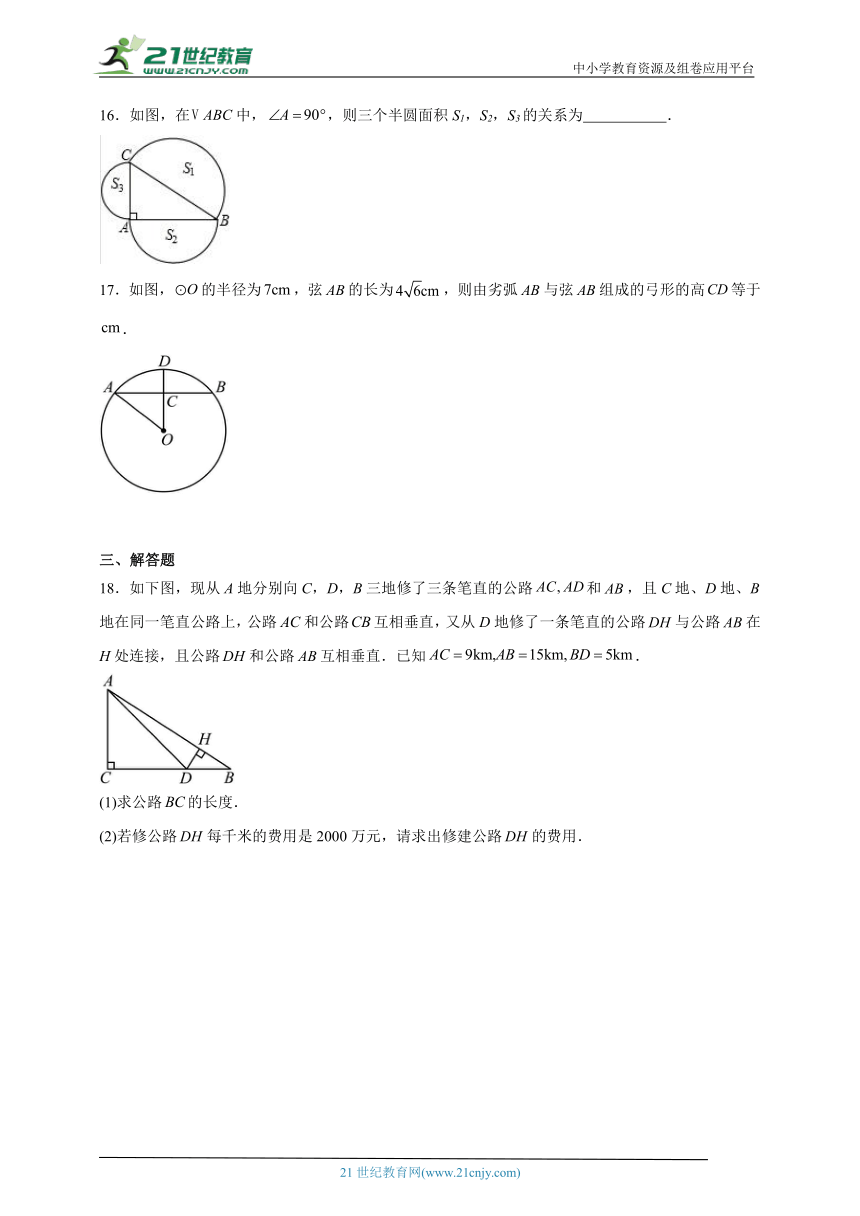
16.如图,在中,,则三个半圆面积S1,S2,S3的关系为 .
17.如图,的半径为,弦的长为,则由劣弧与弦组成的弓形的高等于 .
三、解答题
18.如下图,现从A地分别向C,D,B三地修了三条笔直的公路和,且C地、D地、B地在同一笔直公路上,公路和公路互相垂直,又从D地修了一条笔直的公路与公路在H处连接,且公路和公路互相垂直.已知.
(1)求公路的长度.
(2)若修公路每千米的费用是2000万元,请求出修建公路的费用.
19.已知a,b,c是的三边长,,且,试判断的形状.
20.如图,AB是⊙O的直径,点C是弧AB的中点,连接AC、BC,点Q是△ABC内一点,且有∠QAB=∠QCA.
(1)求∠AQC的度数.
(2)线段QA、QC、QB三者之间的数量关系为: ,并说明理由.
(3)若,求∠AQB的度数.
21.如图,学校有一块三角形空地,计划将这块三角形空地分割成四边形和三角形,分别摆放两种不同的花卉.经测量,,,
,,,,求四边形的面积.
22.如图,一个25米长的梯子,斜靠在一竖直的墙上,这时为24米.如果梯子的顶端A沿墙下滑了4米,那么此时梯子的底部B到墙的距离为多少米?
23.小宇同学在布置班级文化园地时,想从一块长为,宽为的长方形纸片上剪下一个腰长为的等腰三角形,并使其中一个顶点在长方形的一边上,另两个顶点落在对边上,请你帮他计算出所剪下的等腰三角形的底边长.
24.如图,在中,,是的垂直平分线,分别交、于点E、D.
(1)求证:是直角三角形;
(2)求的长.
《第一章勾股定理》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C A A D C D A A B C
题号 11 12
答案 A C
1.C
【分析】根据题意可得能够完全覆盖这个三角形的最小圆为外接圆,圆心位于 和 的垂直平分线的交点处,求出,即可求解.
【详解】解:如图,点为外接圆的圆心,则为半径,
故能完全覆盖该三角形的最小圆面的半径是.
故选:C
【点睛】本题主要考查了三角形的外接圆,勾股定理,熟练掌握三角形的外接圆圆心就是三角形三边垂直平分线的交点是解题的关键.
2.A
【分析】本题主要考查的是勾股定理的应用,设水深为x尺,则荷花茎长为尺,根据题意,利用勾股定理列方程解答即可.
【详解】设池塘深为尺,
则,
解得,
故选:A.
3.A
【分析】先根据勾股定理求出各边的长,再根据勾股定理的逆定理判断出的形状即可.
【详解】解:由图形可知:;;,
∴,
∴是直角三角形.
故选:A.
【点睛】本题考查的是勾股定理及其逆定理,熟知如果三角形的三边长a,b,c满足,那么这个三角形就是直角三角形是解答此题的关键.
4.D
【分析】此题主要考查了勾股数,根据勾股数的定义,可以进行判断,解题的关键是要用到勾股数的定义,及勾股定理的逆定理:已知的三边满足,则是直角三角形.
【详解】解:、,故这是一组勾股数,不符合题意;
、,故这是一组勾股数,不符合题意;
、,故这是一组勾股数,不符合题意;
、,故这不是一组勾股数,符合题意;
故选:.
5.C
【分析】本题主要考查了勾股定理的实际应用,设水深为x尺,则这根芦苇的长为尺,由勾股定理可得,解方程即可得到答案.
【详解】解:设水深为x尺,则这根芦苇的长为尺,
由题意得,,
解得,
∴水深为8尺,
故选:C.
6.D
【分析】本题主要考查了勾股定理,根据直角三角形两直角边的平方和等于斜边的平方求解即可.
【详解】解:正方形的面积为:,正方形的面积为:;
在中,,
又 ∵,
∴,
故选:D.
7.A
【分析】本题主要考查了勾股定理与折叠问题,设,,利用勾股定理建立方程,解方程求出,问题随之得解.
【详解】解:由折叠的性质可得,
设,,
在中,由勾股定理得,
∴,
解得,
∴,
∴,
∴,
故选:A.
8.A
【分析】本题考查了勾股定理,垂线段最短的性质,求出的取值范围是解题的关键.
利用勾股定理列式求出,然后根据求出的范围,再选择答案即可.
【详解】解:如图,
∵,,,
∴,
∴,
纵观各选项,只有2.5不在此范围内.
故选:A.
9.B
【分析】本题考查了解直角三角形,勾股定理,先根据余弦的定义计算出,然后利用勾股定理计算出的长.
【详解】解:∵,
∴,
∵,
∴,
∴.
故选:B.
10.C
【分析】由题意可知东北方向和东南方向间刚好是一直角,利用勾股定理解图中直角三角形即可.
【详解】解:∵OA是东北方向,OB是东南方向,
∴∠AOB=90°,
又∵OA=24m,OB=18m,
∴30m.
故选:C.
【点睛】本题考查的知识点是解直角三角形的应用,正确运用勾股定理,善于观察题目的信息是解题以及学好数学的关键.
11.A
【分析】根据题意作图,利用勾股定理即可求解.
【详解】解:根据题意作图如下,
由题意知,,,
,
,
,
,
梯子底端在水平方向上滑动的距离是.
故选A.
【点睛】本题主要考查勾股定理,解题的关键是根据题意作图分析求解.
12.C
【分析】本题考查了勾股定理的证明,面积转化法,完全平方公式,掌握方法是解题的关键.
由图形中的面积关系:梯形的面积直角三角形的面积等腰三角形的面积,正方形的面积小正方形的面积直角三角形的面积,化简即可求解.
【详解】解:甲同学的方案:
由题意得等腰三角形的直角三角形;
梯形的面积直角三角形的面积等腰三角形的面积,
,
整理得,
因此甲同学的方案可以证明勾股定理.
乙同学的方案:
大正方形的面积小正方形的面积直角三角形的面积,
,
,
,
因此乙同学的方案可以证明勾股定理;
故选:C.
13.13
【分析】本题考查了勾股定理,熟练掌握勾股定理是解题的关键.由勾股定理得出斜边长,即可得解.
【详解】解:∵直角三角形的两直角边长为5和12,
∴该三角形的斜边长为.
故答案为:13.
14. 60; .
【分析】根据直角三角形中30°角所对直角边等于斜边的一半的逆定理,可求∠BE的度数;
根据中位线定理可得AM =2,根据折叠的性质和等腰三角形的性质可得M = N =2,过 M 点作MG⊥EF于G ,可求G ,根据勾股定理可求 MG,进一步得到BE ,再根据勾股定理可求 OF ,从而得到 OD.
【详解】∵BE=B,
∴60°;
故填:60;
∵EN =1,
∴由中位线定理得AM =2,
由折叠的性质可得M =2,
∵AD // EF,
∴∠AMB =∠NM,
∵∠AMB =∠MB,
∴∠NM = ∠MB,
∴N =2,
∴E =3, F =2,
∵∠EB=30°,
∴∠OF=∠EB=30°,
∵OF= O,
∴在Rt△OF中,,即,
,
解得 OF =,
过 M 点作MG⊥EF于 G
∴NG = EN =1,
∴G =1,
由勾股定理得 MG =,
∴BE = DF = MG =,
∴OD= DF-OF=.
故答案为:.
【点睛】考查了翻折变换(折叠问题),矩形的性质,勾股定理,关键是得到矩形的宽和E 的长.
15.4或
【分析】本题考查了勾股定理,熟知任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.
由于直角三角形的斜边不能确定,故分是斜边与直角边两种情况进行解答.
【详解】解:当是直角边时,,
当是斜边时,,
故答案为:4或.
16.
【分析】分别用、和表示出、、,然后根据即可得出、、的关系.
【详解】解:在中,,
,
,,,
,
即.
故答案为:.
【点睛】本题主要考查了勾股定理的应用.解题的关键是勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.
17.2
【分析】根据垂径定理,构造直角三角形,然后利用勾股定理求出的长,即可获得答案.
【详解】解:根据垂径定理,可得,,
则在中,,
∴.
故答案为:2.
【点睛】本题主要考查了垂径定理、勾股定理等知识,熟练掌握垂径定理是解题关键.
18.(1)
(2)(万元)
【分析】本题考查了勾股定理、三角形面积公式及其应用,解题的关键在于利用勾股定理计算直角三角形的边长,通过三角形面积的不同表示方法建立等式求解未知量,最终计算所需费用,体现了数学知识在实际问题中的综合运用.
(1)利用直角三角形中勾股定理求;
(2)先通过与的长度差得到,再利用三角形面积的两种表示方法建立等式求出,最后计算费用.
【详解】解:(1)由题意,得,
所以由勾股定理,得,所以.
(2)因为,
所以,
所以,
所以修建公路的费用为(万元).
19.直角三角形
【分析】本题主要考查的就是比例的性质以及直角三角形的判定.设,可以根据求得k的值,进而求得a、b、c的值,再根据勾股定理的逆定理,即可判断的形状,
【详解】解:设,
则,,.
因为,
所以.解得.
所以,,.
因为,,
所以.
所以为直角三角形.
20.(1)135°;(2)AQ2+2QC2=BQ2,理由见详解;(3)150°
【分析】(1)先证是等腰直角三角形,可得∠QAB+∠QAC=∠BAC=45°,进而即可得到答案;
(2)把CQ绕点C顺时针旋转90°得到CQ’,连接QQ’,AQ’,则是等腰直角三角形,再证,∠AQQ’=135°-45°=90°,进而即可得到答案;
(3)设CQ=3x,AQ=,则QQ’=3x,从而得tan∠AQ’Q=,即:∠AQ’Q=30°,结合,即可得到答案.
【详解】解:(1)∵AB是⊙O的直径,点C是弧AB的中点,
∴是等腰直角三角形,
∴∠QAB+∠QAC=∠BAC=45°,
∵∠QAB=∠QCA,
∴∠QCA +∠QAC=45°,
∴∠AQC=180°-(∠QCA +∠QAC)=135°;
(2)如图:把CQ绕点C顺时针旋转90°得到CQ’,连接QQ’,AQ’,则是等腰直角三角形,
∴∠CQQ’=45°,QQ’=QC,
∵∠QCQ’=∠ACB=90°,
∴∠ACQ’=∠BCQ,
又∵AC=BC,CQ=CQ’,
∴,
∴AQ’=BQ,
∵∠AQC=135°,
∴∠AQQ’=135°-45°=90°,
∴AQ2+QQ’2=AQ’2,
∴AQ2+2QC2=BQ2;
(3)∵,
∴设CQ=3x,AQ=,则QQ’=3x,
∴tan∠AQ’Q=,即:∠AQ’Q=30°,
∴∠AQ’C=30°+45°=75°,
∵,
∴∠BQC=∠AQ’C=75°,
∴∠AQB=360°-135°-75°=150°.
【点睛】本题主要考查圆的综合以及全等三角形的判定和性质,旋转的性质,勾股定理,锐角三角函数,添加辅助线构造全等三角形是解题的关键.
21.
【分析】本题考查勾股定理及其逆定理,三角形面积公式等.根据题意可得,继而得到,,再利用三角形面积公式即可得到本题答案.
【详解】解:∵,
∴,
∵,
∴,,
∵,,
∴,
∴.
22.15米
【分析】此题考查了勾股定理的应用.先求出的长度,再根据勾股定理进行计算即可.
【详解】解:在中,米,
(米),
所以,
所以米,
所以此时梯子的底部B到墙的距离为15米.
23.或或
【分析】此题考查了等腰三角形的基本性质及运用勾股定理求解三角形的边长.关键是要进行分类讨论,不要漏解.
分两种情况:(1)当底边在长方形的长边上时;(2)当腰在长方形的长边上时,再根据腰的不同分两种情况;然后根据勾股定理求出底边边长.
【详解】解:分三种情况考虑:
(1)当底边在长方形的长边上时,如图1,
.
,;
(2)当腰在长方形的长边上时,
Ⅰ、如图2,
,,
;
Ⅱ、如图3,
,,
;
故等腰三角形的底边长为或或.
24.(1)见解析
(2)
【分析】本题考查勾股定理,勾股定理逆定理,垂直平分线性质,解题的关键是先证明直角,再根据垂直平分线性质转换线段,根据勾股定理列方程求解.
(1)根据勾股定理逆定理即可证明;
(2)连接,根据是的垂直平分线,得到,设,则,在中,根据勾股定理列方程求解即可得到答案.
【详解】(1)证明:∵,,,
∴
∴
∴是直角三角形;
(2)解:连接,
∵是的垂直平分线,
∴,
∴设,则,
∵在中,,
∴,
∴,
∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第一章勾股定理
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,将放在每个小正方形的边长为1的网格中,点,,均落在格点上,用一个圆面去覆盖,能够完全覆盖这个三角形的最小圆面的半径是( )
A.4 B. C. D.
2.池塘中有一朵荷花,它直立在水中,荷花高出水面半尺处长着一朵红莲,一阵风吹来把荷花吹倒在一边,红莲倒在水面位置距荷花生长处水平距离为2尺,则池塘深( )
A.3.75尺 B.3.25尺 C.4.25尺 D.3.5尺
3.如图,图中小正方形的边长都为1,的顶点都在格点上,则是( )
A.直角三角形 B.锐角三角形 C.钝角三角形 D.无法判断
4.下列四组数中,不是勾股数的是( )
A. B.
C. D.
5.我国古代数学著作《九章算术》中记载了一个问题:“今有池方一丈,葭()生其中,出水一尺.引葭赴岸,适与岸齐,问水深几何”(丈、尺都是长度单位,1丈尺.)其大意为:有一个水池,水面是一个边长为12尺的正方形,在水池中央有一根芦苇,它高出水面2尺.如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面.水的深度是多少?则水深为( )
A.6尺 B.7尺 C.8尺 D.9尺
6.如图,在中,,分别以、为边作正方形.若,则正方形和正方形的面积和为( )
A.16 B.24 C.32 D.64
7.已知,如图,长方形中,,将此长方形折叠,使点与点重合,折痕为,则的面积为( )
A.6 B.8 C.10 D.12
8.在中,,若,,点P是边上的动点,则的长不可能为( )
A.2.5 B.3.5 C.4 D.4.5
9.如图,在中,已知,那么的长为( )
A. B. C.4 D.5
10.如图,在水塔O的东北方向24m处有一抽水站A,在水塔的 东南方向18m处有一建筑工地B,在AB间建一条直水管,则 水管AB的长为( )
A.40m B.45m C.30m D.35m
11.一架长的梯子斜靠在墙上,梯子底端到墙的距离为.若梯子顶端下滑,那么梯子底端在水平方向上滑动了( )
A. B.小于 C.大于 D.无法确定
12.在学习勾股定理时,甲同学用两个相同的直角三角形和一个等腰三角形构成如图甲所示的直角梯形;乙同学用四个相同的直角三角形构成如图乙所示的大正方形,中间是一个小正方形,甲、乙两位同学给出的构图方案,可以证明勾股定理的是( )
A.甲 B.乙
C.甲,乙都可以 D.甲,乙都不可以
二、填空题
13.直角三角形的两直角边长为5和12,则该三角形的斜边长为 .
14.如图,对折矩形纸片ABCD,使AD和BC重合,得到折痕EF;把纸片展平再折,使点A落在EF上的点处,则 度,折叠后折痕为BM,BM与EF相交于点N,如果直线交CD于点O,,,则OD= .
15.中,,,则 .
16.如图,在中,,则三个半圆面积S1,S2,S3的关系为 .
17.如图,的半径为,弦的长为,则由劣弧与弦组成的弓形的高等于 .
三、解答题
18.如下图,现从A地分别向C,D,B三地修了三条笔直的公路和,且C地、D地、B地在同一笔直公路上,公路和公路互相垂直,又从D地修了一条笔直的公路与公路在H处连接,且公路和公路互相垂直.已知.
(1)求公路的长度.
(2)若修公路每千米的费用是2000万元,请求出修建公路的费用.
19.已知a,b,c是的三边长,,且,试判断的形状.
20.如图,AB是⊙O的直径,点C是弧AB的中点,连接AC、BC,点Q是△ABC内一点,且有∠QAB=∠QCA.
(1)求∠AQC的度数.
(2)线段QA、QC、QB三者之间的数量关系为: ,并说明理由.
(3)若,求∠AQB的度数.
21.如图,学校有一块三角形空地,计划将这块三角形空地分割成四边形和三角形,分别摆放两种不同的花卉.经测量,,,
,,,,求四边形的面积.
22.如图,一个25米长的梯子,斜靠在一竖直的墙上,这时为24米.如果梯子的顶端A沿墙下滑了4米,那么此时梯子的底部B到墙的距离为多少米?
23.小宇同学在布置班级文化园地时,想从一块长为,宽为的长方形纸片上剪下一个腰长为的等腰三角形,并使其中一个顶点在长方形的一边上,另两个顶点落在对边上,请你帮他计算出所剪下的等腰三角形的底边长.
24.如图,在中,,是的垂直平分线,分别交、于点E、D.
(1)求证:是直角三角形;
(2)求的长.
《第一章勾股定理》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C A A D C D A A B C
题号 11 12
答案 A C
1.C
【分析】根据题意可得能够完全覆盖这个三角形的最小圆为外接圆,圆心位于 和 的垂直平分线的交点处,求出,即可求解.
【详解】解:如图,点为外接圆的圆心,则为半径,
故能完全覆盖该三角形的最小圆面的半径是.
故选:C
【点睛】本题主要考查了三角形的外接圆,勾股定理,熟练掌握三角形的外接圆圆心就是三角形三边垂直平分线的交点是解题的关键.
2.A
【分析】本题主要考查的是勾股定理的应用,设水深为x尺,则荷花茎长为尺,根据题意,利用勾股定理列方程解答即可.
【详解】设池塘深为尺,
则,
解得,
故选:A.
3.A
【分析】先根据勾股定理求出各边的长,再根据勾股定理的逆定理判断出的形状即可.
【详解】解:由图形可知:;;,
∴,
∴是直角三角形.
故选:A.
【点睛】本题考查的是勾股定理及其逆定理,熟知如果三角形的三边长a,b,c满足,那么这个三角形就是直角三角形是解答此题的关键.
4.D
【分析】此题主要考查了勾股数,根据勾股数的定义,可以进行判断,解题的关键是要用到勾股数的定义,及勾股定理的逆定理:已知的三边满足,则是直角三角形.
【详解】解:、,故这是一组勾股数,不符合题意;
、,故这是一组勾股数,不符合题意;
、,故这是一组勾股数,不符合题意;
、,故这不是一组勾股数,符合题意;
故选:.
5.C
【分析】本题主要考查了勾股定理的实际应用,设水深为x尺,则这根芦苇的长为尺,由勾股定理可得,解方程即可得到答案.
【详解】解:设水深为x尺,则这根芦苇的长为尺,
由题意得,,
解得,
∴水深为8尺,
故选:C.
6.D
【分析】本题主要考查了勾股定理,根据直角三角形两直角边的平方和等于斜边的平方求解即可.
【详解】解:正方形的面积为:,正方形的面积为:;
在中,,
又 ∵,
∴,
故选:D.
7.A
【分析】本题主要考查了勾股定理与折叠问题,设,,利用勾股定理建立方程,解方程求出,问题随之得解.
【详解】解:由折叠的性质可得,
设,,
在中,由勾股定理得,
∴,
解得,
∴,
∴,
∴,
故选:A.
8.A
【分析】本题考查了勾股定理,垂线段最短的性质,求出的取值范围是解题的关键.
利用勾股定理列式求出,然后根据求出的范围,再选择答案即可.
【详解】解:如图,
∵,,,
∴,
∴,
纵观各选项,只有2.5不在此范围内.
故选:A.
9.B
【分析】本题考查了解直角三角形,勾股定理,先根据余弦的定义计算出,然后利用勾股定理计算出的长.
【详解】解:∵,
∴,
∵,
∴,
∴.
故选:B.
10.C
【分析】由题意可知东北方向和东南方向间刚好是一直角,利用勾股定理解图中直角三角形即可.
【详解】解:∵OA是东北方向,OB是东南方向,
∴∠AOB=90°,
又∵OA=24m,OB=18m,
∴30m.
故选:C.
【点睛】本题考查的知识点是解直角三角形的应用,正确运用勾股定理,善于观察题目的信息是解题以及学好数学的关键.
11.A
【分析】根据题意作图,利用勾股定理即可求解.
【详解】解:根据题意作图如下,
由题意知,,,
,
,
,
,
梯子底端在水平方向上滑动的距离是.
故选A.
【点睛】本题主要考查勾股定理,解题的关键是根据题意作图分析求解.
12.C
【分析】本题考查了勾股定理的证明,面积转化法,完全平方公式,掌握方法是解题的关键.
由图形中的面积关系:梯形的面积直角三角形的面积等腰三角形的面积,正方形的面积小正方形的面积直角三角形的面积,化简即可求解.
【详解】解:甲同学的方案:
由题意得等腰三角形的直角三角形;
梯形的面积直角三角形的面积等腰三角形的面积,
,
整理得,
因此甲同学的方案可以证明勾股定理.
乙同学的方案:
大正方形的面积小正方形的面积直角三角形的面积,
,
,
,
因此乙同学的方案可以证明勾股定理;
故选:C.
13.13
【分析】本题考查了勾股定理,熟练掌握勾股定理是解题的关键.由勾股定理得出斜边长,即可得解.
【详解】解:∵直角三角形的两直角边长为5和12,
∴该三角形的斜边长为.
故答案为:13.
14. 60; .
【分析】根据直角三角形中30°角所对直角边等于斜边的一半的逆定理,可求∠BE的度数;
根据中位线定理可得AM =2,根据折叠的性质和等腰三角形的性质可得M = N =2,过 M 点作MG⊥EF于G ,可求G ,根据勾股定理可求 MG,进一步得到BE ,再根据勾股定理可求 OF ,从而得到 OD.
【详解】∵BE=B,
∴60°;
故填:60;
∵EN =1,
∴由中位线定理得AM =2,
由折叠的性质可得M =2,
∵AD // EF,
∴∠AMB =∠NM,
∵∠AMB =∠MB,
∴∠NM = ∠MB,
∴N =2,
∴E =3, F =2,
∵∠EB=30°,
∴∠OF=∠EB=30°,
∵OF= O,
∴在Rt△OF中,,即,
,
解得 OF =,
过 M 点作MG⊥EF于 G
∴NG = EN =1,
∴G =1,
由勾股定理得 MG =,
∴BE = DF = MG =,
∴OD= DF-OF=.
故答案为:.
【点睛】考查了翻折变换(折叠问题),矩形的性质,勾股定理,关键是得到矩形的宽和E 的长.
15.4或
【分析】本题考查了勾股定理,熟知任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.
由于直角三角形的斜边不能确定,故分是斜边与直角边两种情况进行解答.
【详解】解:当是直角边时,,
当是斜边时,,
故答案为:4或.
16.
【分析】分别用、和表示出、、,然后根据即可得出、、的关系.
【详解】解:在中,,
,
,,,
,
即.
故答案为:.
【点睛】本题主要考查了勾股定理的应用.解题的关键是勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.
17.2
【分析】根据垂径定理,构造直角三角形,然后利用勾股定理求出的长,即可获得答案.
【详解】解:根据垂径定理,可得,,
则在中,,
∴.
故答案为:2.
【点睛】本题主要考查了垂径定理、勾股定理等知识,熟练掌握垂径定理是解题关键.
18.(1)
(2)(万元)
【分析】本题考查了勾股定理、三角形面积公式及其应用,解题的关键在于利用勾股定理计算直角三角形的边长,通过三角形面积的不同表示方法建立等式求解未知量,最终计算所需费用,体现了数学知识在实际问题中的综合运用.
(1)利用直角三角形中勾股定理求;
(2)先通过与的长度差得到,再利用三角形面积的两种表示方法建立等式求出,最后计算费用.
【详解】解:(1)由题意,得,
所以由勾股定理,得,所以.
(2)因为,
所以,
所以,
所以修建公路的费用为(万元).
19.直角三角形
【分析】本题主要考查的就是比例的性质以及直角三角形的判定.设,可以根据求得k的值,进而求得a、b、c的值,再根据勾股定理的逆定理,即可判断的形状,
【详解】解:设,
则,,.
因为,
所以.解得.
所以,,.
因为,,
所以.
所以为直角三角形.
20.(1)135°;(2)AQ2+2QC2=BQ2,理由见详解;(3)150°
【分析】(1)先证是等腰直角三角形,可得∠QAB+∠QAC=∠BAC=45°,进而即可得到答案;
(2)把CQ绕点C顺时针旋转90°得到CQ’,连接QQ’,AQ’,则是等腰直角三角形,再证,∠AQQ’=135°-45°=90°,进而即可得到答案;
(3)设CQ=3x,AQ=,则QQ’=3x,从而得tan∠AQ’Q=,即:∠AQ’Q=30°,结合,即可得到答案.
【详解】解:(1)∵AB是⊙O的直径,点C是弧AB的中点,
∴是等腰直角三角形,
∴∠QAB+∠QAC=∠BAC=45°,
∵∠QAB=∠QCA,
∴∠QCA +∠QAC=45°,
∴∠AQC=180°-(∠QCA +∠QAC)=135°;
(2)如图:把CQ绕点C顺时针旋转90°得到CQ’,连接QQ’,AQ’,则是等腰直角三角形,
∴∠CQQ’=45°,QQ’=QC,
∵∠QCQ’=∠ACB=90°,
∴∠ACQ’=∠BCQ,
又∵AC=BC,CQ=CQ’,
∴,
∴AQ’=BQ,
∵∠AQC=135°,
∴∠AQQ’=135°-45°=90°,
∴AQ2+QQ’2=AQ’2,
∴AQ2+2QC2=BQ2;
(3)∵,
∴设CQ=3x,AQ=,则QQ’=3x,
∴tan∠AQ’Q=,即:∠AQ’Q=30°,
∴∠AQ’C=30°+45°=75°,
∵,
∴∠BQC=∠AQ’C=75°,
∴∠AQB=360°-135°-75°=150°.
【点睛】本题主要考查圆的综合以及全等三角形的判定和性质,旋转的性质,勾股定理,锐角三角函数,添加辅助线构造全等三角形是解题的关键.
21.
【分析】本题考查勾股定理及其逆定理,三角形面积公式等.根据题意可得,继而得到,,再利用三角形面积公式即可得到本题答案.
【详解】解:∵,
∴,
∵,
∴,,
∵,,
∴,
∴.
22.15米
【分析】此题考查了勾股定理的应用.先求出的长度,再根据勾股定理进行计算即可.
【详解】解:在中,米,
(米),
所以,
所以米,
所以此时梯子的底部B到墙的距离为15米.
23.或或
【分析】此题考查了等腰三角形的基本性质及运用勾股定理求解三角形的边长.关键是要进行分类讨论,不要漏解.
分两种情况:(1)当底边在长方形的长边上时;(2)当腰在长方形的长边上时,再根据腰的不同分两种情况;然后根据勾股定理求出底边边长.
【详解】解:分三种情况考虑:
(1)当底边在长方形的长边上时,如图1,
.
,;
(2)当腰在长方形的长边上时,
Ⅰ、如图2,
,,
;
Ⅱ、如图3,
,,
;
故等腰三角形的底边长为或或.
24.(1)见解析
(2)
【分析】本题考查勾股定理,勾股定理逆定理,垂直平分线性质,解题的关键是先证明直角,再根据垂直平分线性质转换线段,根据勾股定理列方程求解.
(1)根据勾股定理逆定理即可证明;
(2)连接,根据是的垂直平分线,得到,设,则,在中,根据勾股定理列方程求解即可得到答案.
【详解】(1)证明:∵,,,
∴
∴
∴是直角三角形;
(2)解:连接,
∵是的垂直平分线,
∴,
∴设,则,
∵在中,,
∴,
∴,
∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
