1.1探索勾股定理同步练习(含解析)北师大版数学八年级上册
文档属性
| 名称 | 1.1探索勾股定理同步练习(含解析)北师大版数学八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-24 20:50:01 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
1.1探索勾股定理
学校:___________姓名:___________班级:___________考号:___________
一、单选题
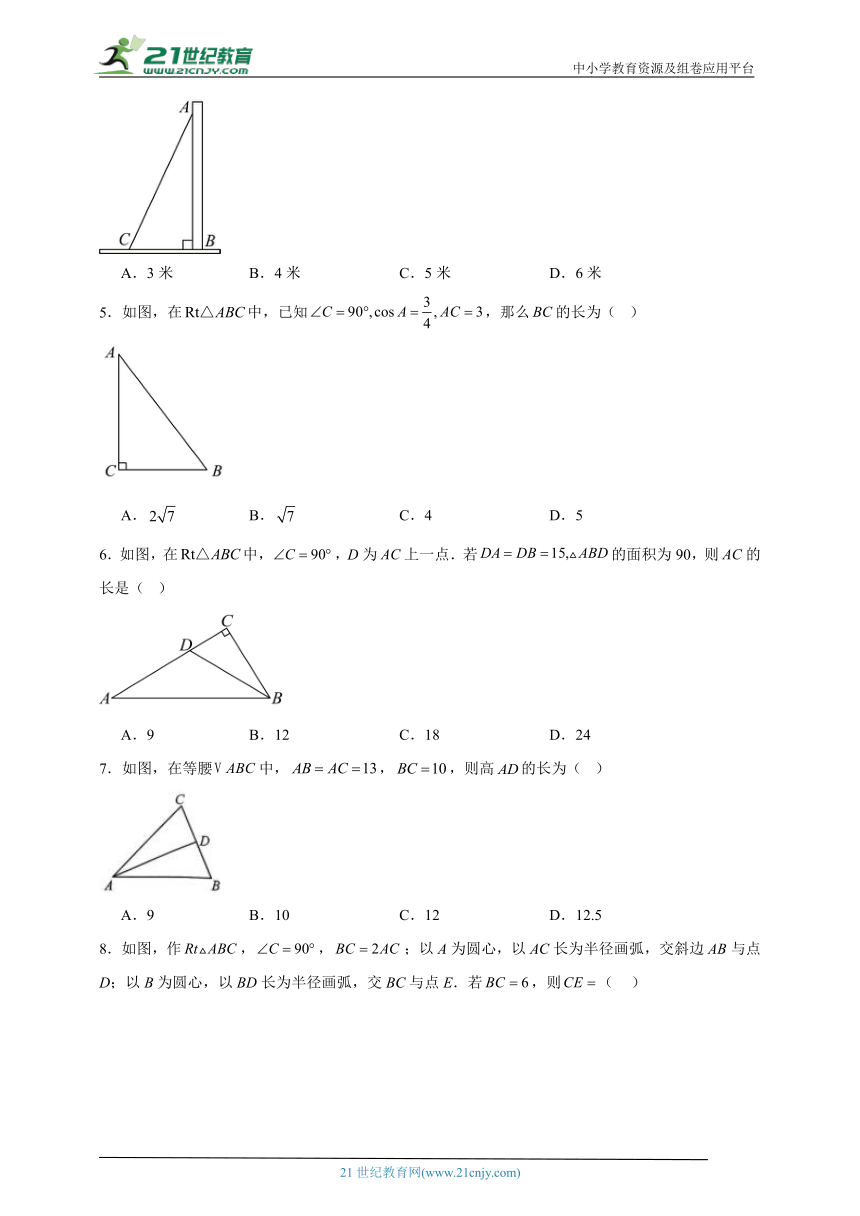
1.如图是我国古代数学家赵爽为《周髀算经》作注解时给出的“弦图”,它解决的数学问题是( )
A.勾股定理 B.三角形内角和定理
C.三角形全等 D.中心对称图形
2.如图,,点为边上的两点,且,连结,则下列结论:①;②;③;④,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
3.如图,已知⊙O的半径为4,M是⊙O内一点,且OM=2,则过点M的所有弦中,弦长是整数的共有( )
A.1条 B.2条 C.3条 D.4条
4.为了固定垂直于地面的木桩,工人们在木桩离地面高4米的点A拉了一根长5米的钢丝,另一头固定在地面的处(接头处长度不计),则点与木桩底部的距离应为( )
A.3米 B.4米 C.5米 D.6米
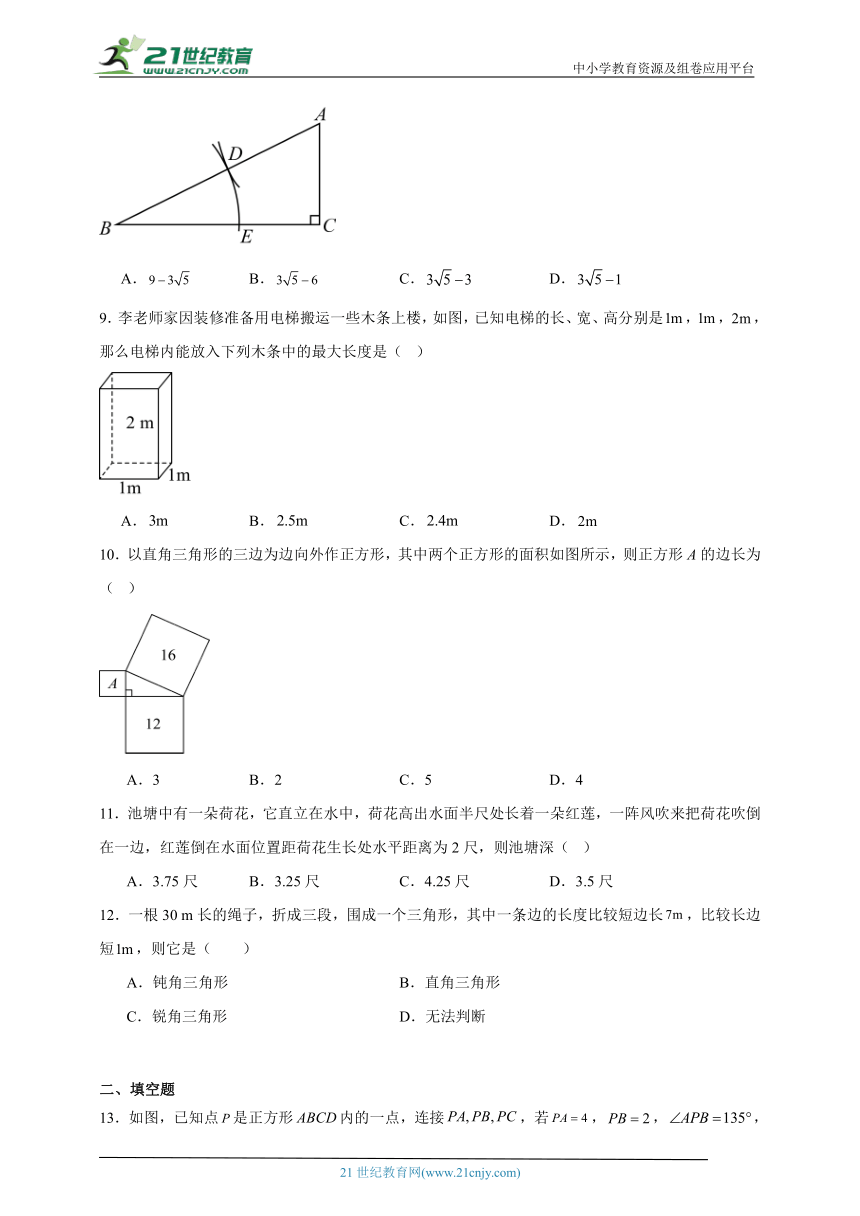
5.如图,在中,已知,那么的长为( )
A. B. C.4 D.5
6.如图,在中,,D为上一点.若的面积为90,则的长是( )
A.9 B.12 C.18 D.24
7.如图,在等腰中,,,则高的长为( )
A.9 B.10 C.12 D.12.5
8.如图,作,,;以A为圆心,以AC长为半径画弧,交斜边AB与点D;以B为圆心,以BD长为半径画弧,交BC与点E.若,则( )
A. B. C. D.
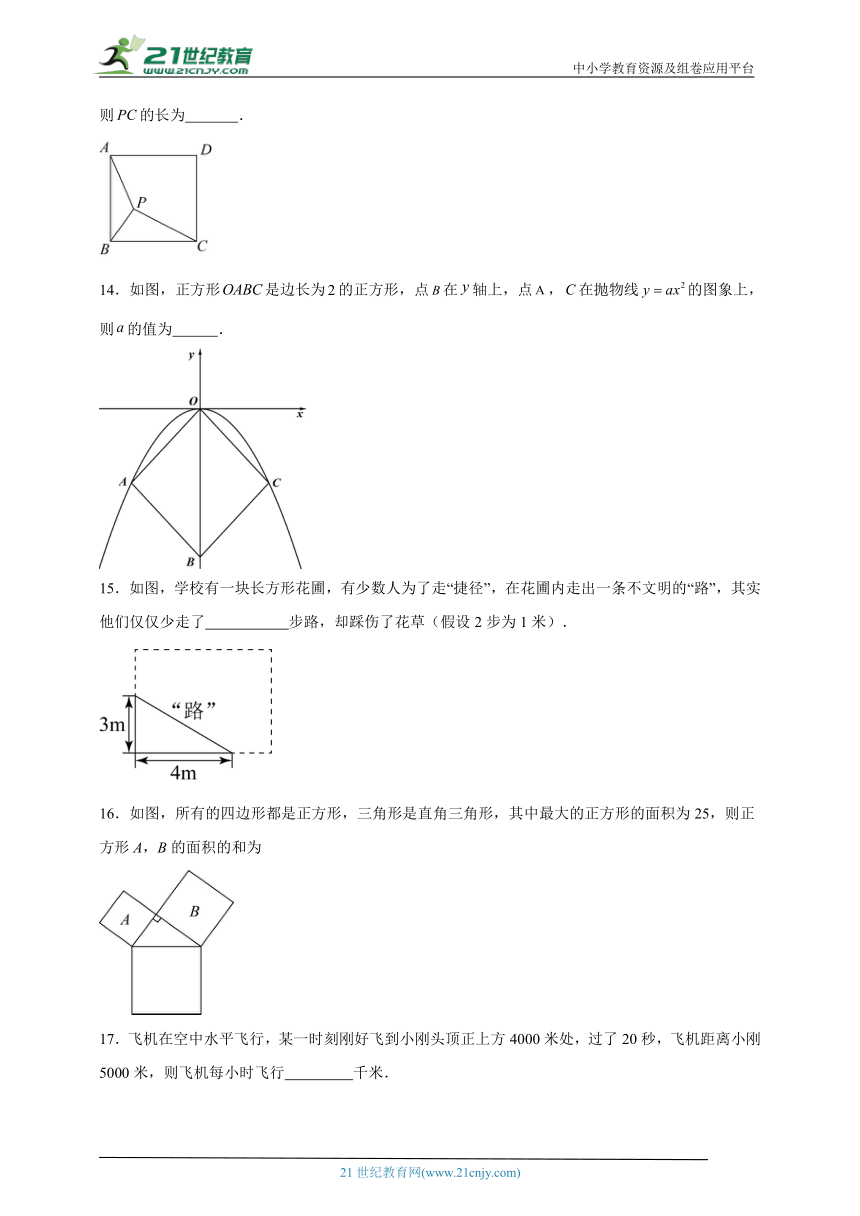
9.李老师家因装修准备用电梯搬运一些木条上楼,如图,已知电梯的长、宽、高分别是,,,那么电梯内能放入下列木条中的最大长度是( )
A. B. C. D.
10.以直角三角形的三边为边向外作正方形,其中两个正方形的面积如图所示,则正方形A的边长为( )
A.3 B.2 C.5 D.4
11.池塘中有一朵荷花,它直立在水中,荷花高出水面半尺处长着一朵红莲,一阵风吹来把荷花吹倒在一边,红莲倒在水面位置距荷花生长处水平距离为2尺,则池塘深( )
A.3.75尺 B.3.25尺 C.4.25尺 D.3.5尺
12.一根30 m长的绳子,折成三段,围成一个三角形,其中一条边的长度比较短边长,比较长边短,则它是( )
A.钝角三角形 B.直角三角形
C.锐角三角形 D.无法判断
二、填空题
13.如图,已知点是正方形内的一点,连接,若,,,则的长为 .
14.如图,正方形是边长为的正方形,点在轴上,点,在抛物线的图象上,则的值为 .
15.如图,学校有一块长方形花圃,有少数人为了走“捷径”,在花圃内走出一条不文明的“路”,其实他们仅仅少走了 步路,却踩伤了花草(假设2步为1米).
16.如图,所有的四边形都是正方形,三角形是直角三角形,其中最大的正方形的面积为25,则正方形A,B的面积的和为
17.飞机在空中水平飞行,某一时刻刚好飞到小刚头顶正上方4000米处,过了20秒,飞机距离小刚5000米,则飞机每小时飞行 千米.
三、解答题
18.《九章算术》“勾股”章有一题:“今有户高多于广六尺八寸,两隅相去适一丈.问户高、广各几何.”
大意是说:已知长方形门的高比宽多6尺8寸,门的对角线长1丈,那么门的高和宽各是多少?
19.如图,各边的长如图所示,求的面积.
20.如图,图中所有的三角形都是直角三角形,四边形都是正方形.已知正方形A,B,C,D的边长分别是12,16,9,12,求最大正方形E的面积.
21.某地一楼房发生火灾,消防队员决定用消防车上的云梯救人,示意图如下图所示.已知云梯最多只能伸长到,消防车高.救人时云梯伸长至最长,在完成从高的B处救人后,还要从高的D处救人.求这时消防车从A处向着火的楼房靠近的距离.
22.如图,地面上放着一个小凳子(与地面平行),点A到墙面(墙面与地面垂直)的距离为.在图①中,一木杆的一端与墙角O重合,另一端靠在点A处,.
(1)求小凳子的高度;
(2)在图②中另一木杆的一端与点B重合,另一端靠在墙上的点C处.若,木杆比凳宽长,求小凳子宽和木杆的长度.
23.1400多年前,我国隋朝建造的赵州石拱桥(如图)是圆弧形,它的跨度(即弧所对的弦长)为,拱高(即弧的中点到弦的距离)为,求桥拱所在圆的半径(结果精确到).
24.某菜农修建一个塑料大棚(如图),若棚宽,高,长,求覆盖在顶上的塑料薄膜的面积.
《1.1探索勾股定理》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A C C A B D C A C B
题号 11 12
答案 A B
1.A
【分析】本题考查对勾股定理的证明,掌握“弦图”的作用是解题的关键.根据“弦图”是解决勾股定理的证明的解答即可.
【详解】解:∵“弦图”是利用面积关系证明勾股定理的,
∴“弦图”解决的数学问题是:勾股定理.
故选:A.
2.C
【分析】本题考查了全等三角形的判定与性质、勾股定理.熟练掌握全等三角形的判定与性质、勾股定理是解题的关键.
利用已知条件证明三角形全等从而得出边和角的关系是解题的关键,再利用三角形的性质判断各个结论的正确性即可.
【详解】解: ,,
,
在与中,
,
,故①正确;
,
,
,
,
在与中,
,
,
,,
在中,,
,故③正确;
,
,
,
,
在中,,
,
,故④正确;
由题干条件无法证明出,
综上所述,其中正确的有①③④,共3个.
故选C.
3.C
【分析】过点M作AB⊥OM交⊙O于点A、B,根据勾股定理求出AM,根据垂径定理求出AB,进而得到答案.
【详解】解:过点M作AB⊥OM交⊙O于点A、B,连接OA,
则AM=BM=AB,
在Rt△AOM中,AM===,
∴AB=2AM=,
则≤过点M的所有弦≤8,
则弦长是整数的共有长度为7的两条,长度为8的一条,共三条,
故选:C.
【点睛】本题考查了垂径定理,勾股定理,掌握垂直于选的直径平分这条弦,并平分弦所对的两条弧是解题关键.
4.A
【分析】本题考查了勾股定理,熟练掌握勾股定理是解题的关键.
根据勾股定理即可得到结论.
【详解】解:∵
∴,
在中,米,米。
∴,
米 ,
故选:A.
5.B
【分析】本题考查了解直角三角形,勾股定理,先根据余弦的定义计算出,然后利用勾股定理计算出的长.
【详解】解:∵,
∴,
∵,
∴,
∴.
故选:B.
6.D
【分析】本题考查了三角形面积公式及勾股定理,根据为中上的高及面积,可得,再利用勾股定理可求得,即可求解.
【详解】解:∵,的面积为90,
∴,解得:,
∵,
∴,
∴,
故选:D.
7.C
【分析】本题主要考查了等腰三角形的性质和勾股定理.
首先根据等腰三角形“三线合一”的性质可得,然后在中由勾股定理计算的长即可.
【详解】解:∵,,,
∴,
∴在中,
故选:C
8.A
【分析】根据勾股定理求出AB,再根据圆的定义可求得AD=AC,BE=BD即可求解.
【详解】解:∵,,
∴AC=3,
在中,,由勾股定理得:
,
由题意,AD=AC=3,BE=BD=AB-AD=-3,
∴CE=BC-BE=6-(-3)=9-,
故选:A.
【点睛】本题考查圆的定义、勾股定理,熟练掌握勾股定理是解答的关键.
9.C
【分析】本题考查了勾股定理.电梯是个长方体,电梯中能放下的最大长度就是长方体对角线的长度,连接、构造直角三角形,利用勾股定理求解即可.
【详解】解:如下图所示,
电梯中能放下的最大长度就是线段的长度,
,
,
,
故选:C.
10.B
【分析】本题考查了勾股定理,解题关键是掌握勾股定理.
直接利用勾股定理求解.
【详解】解:正方形A的边长为,
故选:B.
11.A
【分析】本题主要考查的是勾股定理的应用,设水深为x尺,则荷花茎长为尺,根据题意,利用勾股定理列方程解答即可.
【详解】设池塘深为尺,
则,
解得,
故选:A.
12.B
【分析】本题主要考查了一元一次方程的应用、勾股定理等知识点,根据题意列出方程、求出三边是解题的关键.
设“其中一条边”的长为,再根据意义列一元一次方程,进而求得三边,最后根据勾股定理即可解答.
【详解】解:设“其中一条边”的长为,则有,
解得:.
故三边长分别为5,12,13,
∵,
∴它为直角三角形.
故选B.
13.
【分析】根据题意,将绕点顺时针旋转得,可得是等腰直角三角形,再根据,可得,根据勾股定理即可求解.
【详解】解:如图所示,正方形,,
∴将绕点顺时针旋转,则与重合,得,
∴,,
∴是等腰直角三角形,
∴,,
∵,,
∴,即,且,
∴在中,,
故答案为:.
【点睛】本题主要考查正方形,直角三角形,勾股定理,旋转的性质的综合,掌握旋转的性质,正方形的性质,直角三角形的勾股定理是解题的关键.
14.//
【分析】连接AC,交y轴于点D,先根据正方形的性质可证得CD=OD,∠ODC=90°,进而设CD=OD=x,利用勾股定理可求得点C的坐标,再将点C坐标代入即可求得答案.
【详解】解:如图,连接AC,交y轴于点D,
∵四边形OABC是边长为的正方形,
∴CD=AC,OD=BD,AC=BD,AC⊥BD,
∴CD=OD,∠ODC=90°,
∴设CD=OD=x,
又∵OC=2,
∴在RtODC中,,
即:,
解得:(舍负),
∴CD=OD=,
又∵点C在第四象限,
∴点C的坐标为(,-),
将点C(,-)代入,
得:,
解得:,
故答案为:.
【点睛】本题考查了正方形的性质,勾股定理的应用以及待定系数法求二次函数解析式,根据正方形的性质求得点C的坐标是解决本题的关键.
15.
【分析】根据勾股定理即可求解.
【详解】解:根据题意得,“路”的长度,即步,
是步,是步,共步,
∴少走了步,
故答案为:步.
【点睛】本题主要考查勾股定理的实际应用,掌握勾股定理是解题的关键.
16.25
【分析】本题主要考查了勾股定理弦图,熟练掌握勾股定理的几何意义是解题的关键.
根据勾股定理的几何意义即可解答.
【详解】解:根据勾股定理的几何意义可得:
正方形A,B的面积的和=最大正方形的面积=25.
故答案为:25.
17.540
【分析】本题考查了勾股定理在实际问题中的运用,由勾股定理计算过了秒,飞机飞行的水平距离,再用速度路程时间解答即可.
【详解】解:飞机飞行的距离为:米,
∴飞行的速度为千米/时,
故答案为:540.
18.门的高为9尺6寸,宽为2尺8寸
【分析】设门高x尺,则宽为尺,根据勾股定理列方程解答.
【详解】解:设门高x尺,则宽为尺,
根据题意,得.
整理,得.
解得(不合题意,舍去).
【点睛】此题考查一元二次方程的实际应用,勾股定理,正确理解题意利用勾股定理列出方程是解题的关键.
19.
【分析】本题考查了勾股定理;先利用勾股定理列方程求出,再根据三角形的面积公式计算即可.
【详解】解:由勾股定理得,
解得,
所以的面积.
20.
【分析】本题主要考查了勾股定理,根据勾股定理可求出正方形F和正方形G的边长,进而可求出正方形E的边长,再根据正方形面积计算公式可得答案.
【详解】解:如图所示,∵正方形A,B的边长分别为12,16,
∴,
在中,由勾股定理得,
∴正方形F的边长为20,
同理可得正方形G的边长为,
∴正方形E的边长为,
∴正方形E的面积为.
21.消防车从处向着火的楼房靠近的距离为
【分析】本题考查了勾股定理的应用,在中,根据勾股定理得到和,于是得到结论.
【详解】解:在中,因为,
所以,
所以.
在中,因为,
所以,
所以,
所以.
故消防车从处向着火的楼房靠近的距离为.
22.(1).
(2)
【分析】(1)过A作垂直于墙面,垂足M,根据勾股定理解答即可;
(2)延长交墙面于点N,根据勾股定理解答即可.
【详解】(1)解:过A作垂直于墙面,垂足M,
根据题意可得,,
在中,,
即凳子的高度为.
(2)解:延长交墙面于点N,可得,
设cm,则,,,
在中,,即,
解得,则.
【点睛】此题考查勾股定理的应用,解题的关键是根据勾股定理解答.
23..
【分析】利用勾股定理和垂径定理解答.
【详解】解:如图,∵,拱桥的跨度AB=37.4m,拱高CD=7.2m,
∴AD=AB=18.7m,
∴AD2=OA2 (OC CD)2,即18.72=AO2 (AO 7.2)2,
解得AO≈27.9m.即圆弧半径为27.9m.
答:桥拱所在圆的半径为27.9m.
【点睛】本题考查了垂径定理和勾股定理,注意数形结合思想与方程思想的应用.
24.
【分析】本题考查勾股定理的应用,首先根据勾股定理求得直角三角形的斜边,即是长方形的宽,再根据长方形的面积公式计算即可.
【详解】解:米,
∴塑料薄膜的面积为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
1.1探索勾股定理
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图是我国古代数学家赵爽为《周髀算经》作注解时给出的“弦图”,它解决的数学问题是( )
A.勾股定理 B.三角形内角和定理
C.三角形全等 D.中心对称图形
2.如图,,点为边上的两点,且,连结,则下列结论:①;②;③;④,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
3.如图,已知⊙O的半径为4,M是⊙O内一点,且OM=2,则过点M的所有弦中,弦长是整数的共有( )
A.1条 B.2条 C.3条 D.4条
4.为了固定垂直于地面的木桩,工人们在木桩离地面高4米的点A拉了一根长5米的钢丝,另一头固定在地面的处(接头处长度不计),则点与木桩底部的距离应为( )
A.3米 B.4米 C.5米 D.6米
5.如图,在中,已知,那么的长为( )
A. B. C.4 D.5
6.如图,在中,,D为上一点.若的面积为90,则的长是( )
A.9 B.12 C.18 D.24
7.如图,在等腰中,,,则高的长为( )
A.9 B.10 C.12 D.12.5
8.如图,作,,;以A为圆心,以AC长为半径画弧,交斜边AB与点D;以B为圆心,以BD长为半径画弧,交BC与点E.若,则( )
A. B. C. D.
9.李老师家因装修准备用电梯搬运一些木条上楼,如图,已知电梯的长、宽、高分别是,,,那么电梯内能放入下列木条中的最大长度是( )
A. B. C. D.
10.以直角三角形的三边为边向外作正方形,其中两个正方形的面积如图所示,则正方形A的边长为( )
A.3 B.2 C.5 D.4
11.池塘中有一朵荷花,它直立在水中,荷花高出水面半尺处长着一朵红莲,一阵风吹来把荷花吹倒在一边,红莲倒在水面位置距荷花生长处水平距离为2尺,则池塘深( )
A.3.75尺 B.3.25尺 C.4.25尺 D.3.5尺
12.一根30 m长的绳子,折成三段,围成一个三角形,其中一条边的长度比较短边长,比较长边短,则它是( )
A.钝角三角形 B.直角三角形
C.锐角三角形 D.无法判断
二、填空题
13.如图,已知点是正方形内的一点,连接,若,,,则的长为 .
14.如图,正方形是边长为的正方形,点在轴上,点,在抛物线的图象上,则的值为 .
15.如图,学校有一块长方形花圃,有少数人为了走“捷径”,在花圃内走出一条不文明的“路”,其实他们仅仅少走了 步路,却踩伤了花草(假设2步为1米).
16.如图,所有的四边形都是正方形,三角形是直角三角形,其中最大的正方形的面积为25,则正方形A,B的面积的和为
17.飞机在空中水平飞行,某一时刻刚好飞到小刚头顶正上方4000米处,过了20秒,飞机距离小刚5000米,则飞机每小时飞行 千米.
三、解答题
18.《九章算术》“勾股”章有一题:“今有户高多于广六尺八寸,两隅相去适一丈.问户高、广各几何.”
大意是说:已知长方形门的高比宽多6尺8寸,门的对角线长1丈,那么门的高和宽各是多少?
19.如图,各边的长如图所示,求的面积.
20.如图,图中所有的三角形都是直角三角形,四边形都是正方形.已知正方形A,B,C,D的边长分别是12,16,9,12,求最大正方形E的面积.
21.某地一楼房发生火灾,消防队员决定用消防车上的云梯救人,示意图如下图所示.已知云梯最多只能伸长到,消防车高.救人时云梯伸长至最长,在完成从高的B处救人后,还要从高的D处救人.求这时消防车从A处向着火的楼房靠近的距离.
22.如图,地面上放着一个小凳子(与地面平行),点A到墙面(墙面与地面垂直)的距离为.在图①中,一木杆的一端与墙角O重合,另一端靠在点A处,.
(1)求小凳子的高度;
(2)在图②中另一木杆的一端与点B重合,另一端靠在墙上的点C处.若,木杆比凳宽长,求小凳子宽和木杆的长度.
23.1400多年前,我国隋朝建造的赵州石拱桥(如图)是圆弧形,它的跨度(即弧所对的弦长)为,拱高(即弧的中点到弦的距离)为,求桥拱所在圆的半径(结果精确到).
24.某菜农修建一个塑料大棚(如图),若棚宽,高,长,求覆盖在顶上的塑料薄膜的面积.
《1.1探索勾股定理》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A C C A B D C A C B
题号 11 12
答案 A B
1.A
【分析】本题考查对勾股定理的证明,掌握“弦图”的作用是解题的关键.根据“弦图”是解决勾股定理的证明的解答即可.
【详解】解:∵“弦图”是利用面积关系证明勾股定理的,
∴“弦图”解决的数学问题是:勾股定理.
故选:A.
2.C
【分析】本题考查了全等三角形的判定与性质、勾股定理.熟练掌握全等三角形的判定与性质、勾股定理是解题的关键.
利用已知条件证明三角形全等从而得出边和角的关系是解题的关键,再利用三角形的性质判断各个结论的正确性即可.
【详解】解: ,,
,
在与中,
,
,故①正确;
,
,
,
,
在与中,
,
,
,,
在中,,
,故③正确;
,
,
,
,
在中,,
,
,故④正确;
由题干条件无法证明出,
综上所述,其中正确的有①③④,共3个.
故选C.
3.C
【分析】过点M作AB⊥OM交⊙O于点A、B,根据勾股定理求出AM,根据垂径定理求出AB,进而得到答案.
【详解】解:过点M作AB⊥OM交⊙O于点A、B,连接OA,
则AM=BM=AB,
在Rt△AOM中,AM===,
∴AB=2AM=,
则≤过点M的所有弦≤8,
则弦长是整数的共有长度为7的两条,长度为8的一条,共三条,
故选:C.
【点睛】本题考查了垂径定理,勾股定理,掌握垂直于选的直径平分这条弦,并平分弦所对的两条弧是解题关键.
4.A
【分析】本题考查了勾股定理,熟练掌握勾股定理是解题的关键.
根据勾股定理即可得到结论.
【详解】解:∵
∴,
在中,米,米。
∴,
米 ,
故选:A.
5.B
【分析】本题考查了解直角三角形,勾股定理,先根据余弦的定义计算出,然后利用勾股定理计算出的长.
【详解】解:∵,
∴,
∵,
∴,
∴.
故选:B.
6.D
【分析】本题考查了三角形面积公式及勾股定理,根据为中上的高及面积,可得,再利用勾股定理可求得,即可求解.
【详解】解:∵,的面积为90,
∴,解得:,
∵,
∴,
∴,
故选:D.
7.C
【分析】本题主要考查了等腰三角形的性质和勾股定理.
首先根据等腰三角形“三线合一”的性质可得,然后在中由勾股定理计算的长即可.
【详解】解:∵,,,
∴,
∴在中,
故选:C
8.A
【分析】根据勾股定理求出AB,再根据圆的定义可求得AD=AC,BE=BD即可求解.
【详解】解:∵,,
∴AC=3,
在中,,由勾股定理得:
,
由题意,AD=AC=3,BE=BD=AB-AD=-3,
∴CE=BC-BE=6-(-3)=9-,
故选:A.
【点睛】本题考查圆的定义、勾股定理,熟练掌握勾股定理是解答的关键.
9.C
【分析】本题考查了勾股定理.电梯是个长方体,电梯中能放下的最大长度就是长方体对角线的长度,连接、构造直角三角形,利用勾股定理求解即可.
【详解】解:如下图所示,
电梯中能放下的最大长度就是线段的长度,
,
,
,
故选:C.
10.B
【分析】本题考查了勾股定理,解题关键是掌握勾股定理.
直接利用勾股定理求解.
【详解】解:正方形A的边长为,
故选:B.
11.A
【分析】本题主要考查的是勾股定理的应用,设水深为x尺,则荷花茎长为尺,根据题意,利用勾股定理列方程解答即可.
【详解】设池塘深为尺,
则,
解得,
故选:A.
12.B
【分析】本题主要考查了一元一次方程的应用、勾股定理等知识点,根据题意列出方程、求出三边是解题的关键.
设“其中一条边”的长为,再根据意义列一元一次方程,进而求得三边,最后根据勾股定理即可解答.
【详解】解:设“其中一条边”的长为,则有,
解得:.
故三边长分别为5,12,13,
∵,
∴它为直角三角形.
故选B.
13.
【分析】根据题意,将绕点顺时针旋转得,可得是等腰直角三角形,再根据,可得,根据勾股定理即可求解.
【详解】解:如图所示,正方形,,
∴将绕点顺时针旋转,则与重合,得,
∴,,
∴是等腰直角三角形,
∴,,
∵,,
∴,即,且,
∴在中,,
故答案为:.
【点睛】本题主要考查正方形,直角三角形,勾股定理,旋转的性质的综合,掌握旋转的性质,正方形的性质,直角三角形的勾股定理是解题的关键.
14.//
【分析】连接AC,交y轴于点D,先根据正方形的性质可证得CD=OD,∠ODC=90°,进而设CD=OD=x,利用勾股定理可求得点C的坐标,再将点C坐标代入即可求得答案.
【详解】解:如图,连接AC,交y轴于点D,
∵四边形OABC是边长为的正方形,
∴CD=AC,OD=BD,AC=BD,AC⊥BD,
∴CD=OD,∠ODC=90°,
∴设CD=OD=x,
又∵OC=2,
∴在RtODC中,,
即:,
解得:(舍负),
∴CD=OD=,
又∵点C在第四象限,
∴点C的坐标为(,-),
将点C(,-)代入,
得:,
解得:,
故答案为:.
【点睛】本题考查了正方形的性质,勾股定理的应用以及待定系数法求二次函数解析式,根据正方形的性质求得点C的坐标是解决本题的关键.
15.
【分析】根据勾股定理即可求解.
【详解】解:根据题意得,“路”的长度,即步,
是步,是步,共步,
∴少走了步,
故答案为:步.
【点睛】本题主要考查勾股定理的实际应用,掌握勾股定理是解题的关键.
16.25
【分析】本题主要考查了勾股定理弦图,熟练掌握勾股定理的几何意义是解题的关键.
根据勾股定理的几何意义即可解答.
【详解】解:根据勾股定理的几何意义可得:
正方形A,B的面积的和=最大正方形的面积=25.
故答案为:25.
17.540
【分析】本题考查了勾股定理在实际问题中的运用,由勾股定理计算过了秒,飞机飞行的水平距离,再用速度路程时间解答即可.
【详解】解:飞机飞行的距离为:米,
∴飞行的速度为千米/时,
故答案为:540.
18.门的高为9尺6寸,宽为2尺8寸
【分析】设门高x尺,则宽为尺,根据勾股定理列方程解答.
【详解】解:设门高x尺,则宽为尺,
根据题意,得.
整理,得.
解得(不合题意,舍去).
【点睛】此题考查一元二次方程的实际应用,勾股定理,正确理解题意利用勾股定理列出方程是解题的关键.
19.
【分析】本题考查了勾股定理;先利用勾股定理列方程求出,再根据三角形的面积公式计算即可.
【详解】解:由勾股定理得,
解得,
所以的面积.
20.
【分析】本题主要考查了勾股定理,根据勾股定理可求出正方形F和正方形G的边长,进而可求出正方形E的边长,再根据正方形面积计算公式可得答案.
【详解】解:如图所示,∵正方形A,B的边长分别为12,16,
∴,
在中,由勾股定理得,
∴正方形F的边长为20,
同理可得正方形G的边长为,
∴正方形E的边长为,
∴正方形E的面积为.
21.消防车从处向着火的楼房靠近的距离为
【分析】本题考查了勾股定理的应用,在中,根据勾股定理得到和,于是得到结论.
【详解】解:在中,因为,
所以,
所以.
在中,因为,
所以,
所以,
所以.
故消防车从处向着火的楼房靠近的距离为.
22.(1).
(2)
【分析】(1)过A作垂直于墙面,垂足M,根据勾股定理解答即可;
(2)延长交墙面于点N,根据勾股定理解答即可.
【详解】(1)解:过A作垂直于墙面,垂足M,
根据题意可得,,
在中,,
即凳子的高度为.
(2)解:延长交墙面于点N,可得,
设cm,则,,,
在中,,即,
解得,则.
【点睛】此题考查勾股定理的应用,解题的关键是根据勾股定理解答.
23..
【分析】利用勾股定理和垂径定理解答.
【详解】解:如图,∵,拱桥的跨度AB=37.4m,拱高CD=7.2m,
∴AD=AB=18.7m,
∴AD2=OA2 (OC CD)2,即18.72=AO2 (AO 7.2)2,
解得AO≈27.9m.即圆弧半径为27.9m.
答:桥拱所在圆的半径为27.9m.
【点睛】本题考查了垂径定理和勾股定理,注意数形结合思想与方程思想的应用.
24.
【分析】本题考查勾股定理的应用,首先根据勾股定理求得直角三角形的斜边,即是长方形的宽,再根据长方形的面积公式计算即可.
【详解】解:米,
∴塑料薄膜的面积为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
