2025年福建省福州市一中中考数学适应性试卷(4月份)(含答案)
文档属性
| 名称 | 2025年福建省福州市一中中考数学适应性试卷(4月份)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 202.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-23 17:13:59 | ||
图片预览




文档简介
2025年福建省福州一中中考数学适应性试卷(4月份)
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.-5的绝对值是( )
A. B. 5 C. -5 D. -
2.手机移动支付给生活带来便捷.如图是小陈某某天微信账单的全部收支明细(正数表示收入,负数表示支出,单位:元),小陈当天微信收支的最终结果是( )
A. 收入36元 B. 支出26元 C. 收入10元 D. 支出10元
3.如图是由四个相同的小正方体组成的立体图形,它的左视图为( )
A.
B.
C.
D.
4.下列各式中,正确的是( )
A. B. C. D.
5.一条古称在称物时的状态如图所示,已知∠1=80°,则∠2=( )
A. 20°
B. 80°
C. 100°
D. 120°
6.如图,A、D是⊙O上的两个点,BC是直径,若∠D=34°,则∠OAC等于( )
A. 68°
B. 58°
C. 72°
D. 56°
7.把如图的五角星绕着它的中心旋转一定角度后与自身重合,则这个旋转角度可能是( )
A. 36°
B. 72°
C. 90°
D. 108°
8.《孙子算经》中有一道题,原文是:今有三人共车,二车空;二人共车,九人步,问人与车各几何?译文为:今有若干人乘车,每3人共乘一车,最终剩余2辆车;若每2人共乘一车,则最终剩余9个人无车可乘,问共有多少人,多少辆车?设共有x人,则可列方程为( )
A. =-9 B. +2= C. -2= D. =+9
9.已知点M(6,a-3),N(-2,a),P(2,a)在同一个函数图象上,则这个函数图象可能是( )
A. B.
C. D.
10.计算机中常用的十六进制是一种逢16进1的计数制,采用数字0~9和字母A~F共16个计数符号,这些符号与十进制的数字的对应关系如表:
十六进制 0 1 2 3 4 5 6
十进制 0 1 2 3 4 5 6
十六进制 8 9 A B C D E
十进制 8 9 10 11 12 13 14
例如,用十六进制表示D+E=1B,用十进制表示也就是13+14=1×16+11,则用十六进制表示E×F=( )
A. 6E B. 2D C. D2 D. 210
二、填空题:本题共6小题,每小题3分,共18分。
11.分解因式:9x2-3xy= ______.
12.如图,在△ABC中,点D,E分别为边AB,AC上的点,且DE∥BC,若AD=5,BD=10,DE=3,则BC的长为______.
13.设x1,x2是一元一次方程2x2-3x-10=0的两根,=______.
14.某学校广播站要新招1名广播员,甲、乙两名同学经过选拔进入复试环节,参加了口语表达、写作能力两项测试,得分如表:
口语表达 写作能力
甲同学 80 90
乙同学 90 80
该学校规定口语表达按60%、写作能力按40%计入总成绩,根据总成绩从高到低择优录取.通过计算,被录取的同学是______.
15.如图,矩形ABCD两组对边分别和坐标轴平行且矩形的对角线交点为原点,点C在函数的图象上,则矩形ABCD的面积为______.
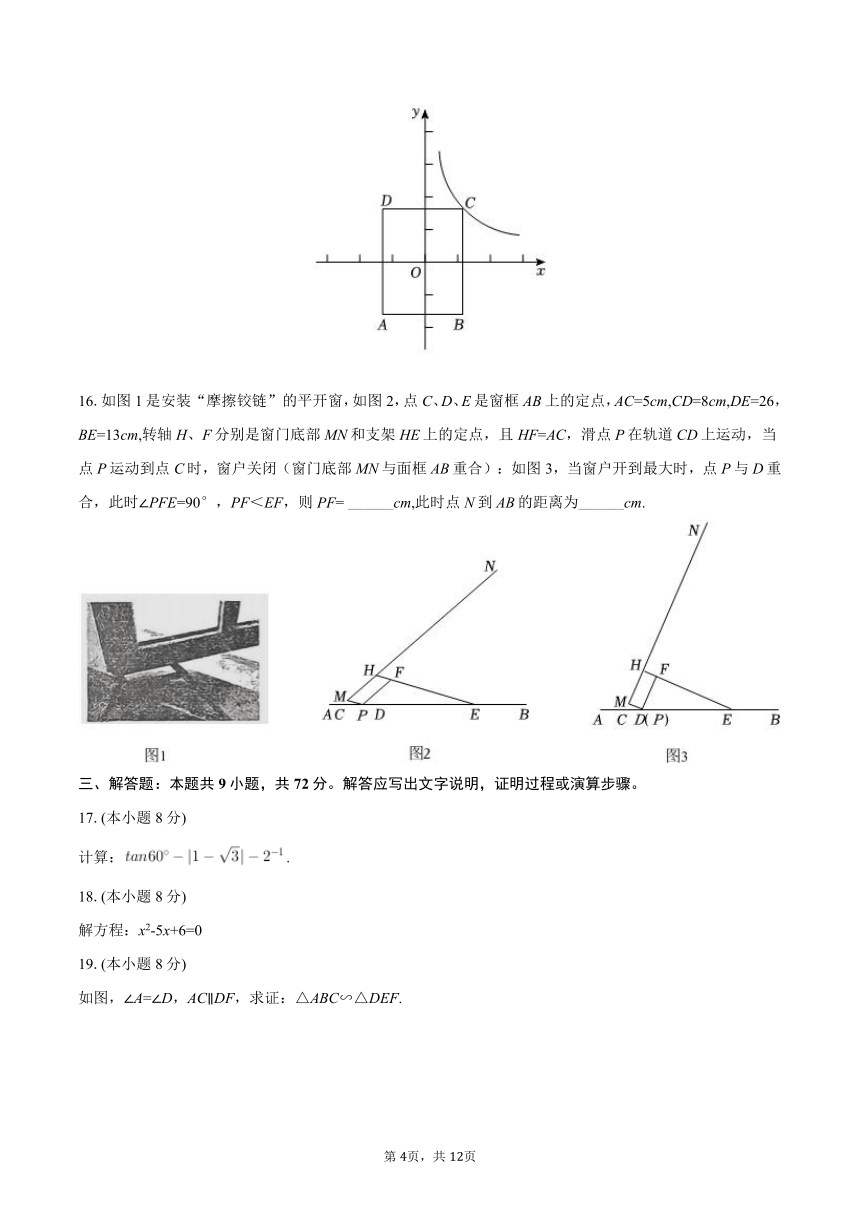
16.如图1是安装“摩擦铰链”的平开窗,如图2,点C、D、E是窗框AB上的定点,AC=5cm,CD=8cm,DE=26,BE=13cm,转轴H、F分别是窗门底部MN和支架HE上的定点,且HF=AC,滑点P在轨道CD上运动,当点P运动到点C时,窗户关闭(窗门底部MN与面框AB重合):如图3,当窗户开到最大时,点P与D重合,此时∠PFE=90°,PF<EF,则PF= ______cm,此时点N到AB的距离为______cm.
三、解答题:本题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.(本小题8分)
计算:.
18.(本小题8分)
解方程:x2-5x+6=0
19.(本小题8分)
如图,∠A=∠D,AC∥DF,求证:△ABC∽△DEF.
20.(本小题8分)
某校的饮水机有温水、开水两个按钮,温水和开水共用一个出水口.温水的温度为30℃,流速为20ml/s;开水的温度为100℃,流速为15ml/s.某学生先接了一会儿温水,又接了一会儿开水,得到一杯210ml温度为60℃的水(不计热损失),求该学生分别接温水和开水的时间.
物理常识
开水和温水混合时会发生热传递,开水放出的热量等于温水吸收的热量,可以转化为:开水的体积×开水降低的温度=温水的体积×温水升高的温度.
21.(本小题8分)
保护环境,人人有责,某校为培养学生“垃圾分类,从我做起”的环保意识,组织开展“游戏互动”、“趣味问答”、“模拟投放”三项活动(分别以A、B、C来依次表示这三项活动).活动开始前,将A,B,C这三个字母分别写在三张无差别不透明的卡片正面上,洗匀后正面向下放在桌面上,小南同学先从中随机抽取一张卡片放回后洗匀,小晶同学从中再随机抽取一张卡片.
(1)求小南抽到参加“趣味问答”活动的概率;
(2)用列表法或画树状图法,求小南和小晶都抽到参加“趣味问答”活动的概率.
22.(本小题8分)
如图,O是半圆的圆心,直径AB=10cm.
(1)分别在半圆上的取点C和点D,顺次连接各点,构成以A,O,C,D为顶点的菱形,请用直尺和圆规求作符合要求的菱形;
(2)求(1)中菱形的面积.
23.(本小题8分)
【阅读材料】用“割尾法”判断一个三位数能否是7的整数倍.
方法:三位数割掉末位数字c得两位数,再用减去c的2倍所得的差为.若是7的整数倍,则是7的整数倍. 注: 举例:对于三位数364,割掉末位数字4得36,36-4×2=28,因为28是7的整数倍,所以364是7的整数倍.
(1)尝试用“割尾法”判断455能否是7的整数倍.
(2)材料中的判断方法是“若是7的整数倍,则是7的整数倍”,请证明这种方法的正确性.
24.(本小题8分)
如图,在△ABC中,AB=AC,∠BAC=90°,点D是△ABC内一点,且CD=CA.
(1)求证:∠ACD=2∠BAD;
(2)将线段DA绕点D顺时针旋转90°得到线段DE,连接AE交CD于点F.
①依题意补全图形;
②若点F恰是CD的中点,用等式表示AE与BD之间的数量关系,并证明.
25.(本小题8分)
根据背景素材,探索解决问题.
测算拉索桥立柱的高
素材1 一条桥身形状和抛物线y= x2相同的拉索桥,桥的跨径OH的水平距离为22米,点O和点H处于同一水平线.
素材2 (1)桥的两根主立柱AB和GL拉出铁索固定桥身,两个立柱中间共有10根拉索(如图);(2)立柱和铁索与桥身的连接点水平等距分布(即相邻的两个连接点的水平距离相等);(3)经测量拉索AC与水平线CE成45°角,从左侧第3个拉索连接点D射出的探测光线DP交立柱AB于点P,从连接点C射出的探测光线CB交立柱于点B,且DP∥CB.
问题解决
任务1 建立模型 以点O为原点,水平线为x轴,以1米为一个单位长度,建立直角坐标系,根据素材1求桥身模型的函数解析式.
任务2 利用模型 根据任务1所求的解析式模型,分别求点D、C的坐标.
任务3 分析计算 若点P恰好为OB中点,根据素材2及任务1和任务2得到的函数模型和数据,求立柱AB的高度.
1.【答案】B
2.【答案】C
3.【答案】A
4.【答案】D
5.【答案】C
6.【答案】D
7.【答案】B
8.【答案】B
9.【答案】A
10.【答案】C
11.【答案】3x(3x-y)
12.【答案】9
13.【答案】5
14.【答案】乙同学
15.【答案】8
16.【答案】10
17.【答案】.
18.【答案】解:∵x2-5x+6=0,
∴(x-2)(x-3)=0,
则x-2=0或x-3=0,
解得x1=2,x2=3.
19.【答案】证明:∵AC∥DF,
∴∠ACB=∠DFE,
∵∠A=∠D,
∴△ABC∽△DEF.
20.【答案】该学生接温水的时间为6s,接开水的时间为6s.
21.【答案】解(1)依题意知抽到参加“趣味问答”的概率为;
(2)树状图如下:
共有9种等可能的结果,其中小南和小晶都抽到参加“趣味问答”活动的结果有1种,
∴小南和小晶都抽到参加“趣味问答”活动的概率为.
22.【答案】见解析;
cm2.
23.【答案】是,理由见解析; 证明见解析.
24.【答案】见解析过程;
①见解析过程;②AE=2BD,理由见解析过程.
25.【答案】解:(1)如图所示,
∵抛物线经过(0,0),(22,0),
∴抛物线的对称轴为直线x=11,
设抛物线解析式为:y=-,
代入(0,0)得:0=-(0-11)2+k,
解得k=,
∴抛物线解析式为:y=-(x-11)2+;
(2)由题意可知,线段OH被均分成11条相等的线段,每段长为(22÷11=2米),
不妨设点C(10,m),D(6,n),
当x=10时,m=-(10-11)2+=2;
当x=6时,n=-(6-11)2+=;
∴C(10,2),D(6,);
(3)设CE与y轴交于点M,作DN⊥y轴于点N,则DN∥CM∥OH,
∴∠3=∠4,∠1=∠2,∠BMC=∠BND,
∵DP∥BC,
∴∠2=∠4,∠1=∠3,
∴△BMC∽△PND,
∴,
∵DN=6,CM=10,OM=2,ON=,OB=2OP,
∴,
解得OP=2,
∴OB=4,
∵∠ACE=45°,
∴∠ACE=∠CAM,
∴AM=CM=10,
∴AB=AM+OM+OB=10+2+4=16.
故立柱AB的高度为16米.
第1页,共1页
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.-5的绝对值是( )
A. B. 5 C. -5 D. -
2.手机移动支付给生活带来便捷.如图是小陈某某天微信账单的全部收支明细(正数表示收入,负数表示支出,单位:元),小陈当天微信收支的最终结果是( )
A. 收入36元 B. 支出26元 C. 收入10元 D. 支出10元
3.如图是由四个相同的小正方体组成的立体图形,它的左视图为( )
A.
B.
C.
D.
4.下列各式中,正确的是( )
A. B. C. D.
5.一条古称在称物时的状态如图所示,已知∠1=80°,则∠2=( )
A. 20°
B. 80°
C. 100°
D. 120°
6.如图,A、D是⊙O上的两个点,BC是直径,若∠D=34°,则∠OAC等于( )
A. 68°
B. 58°
C. 72°
D. 56°
7.把如图的五角星绕着它的中心旋转一定角度后与自身重合,则这个旋转角度可能是( )
A. 36°
B. 72°
C. 90°
D. 108°
8.《孙子算经》中有一道题,原文是:今有三人共车,二车空;二人共车,九人步,问人与车各几何?译文为:今有若干人乘车,每3人共乘一车,最终剩余2辆车;若每2人共乘一车,则最终剩余9个人无车可乘,问共有多少人,多少辆车?设共有x人,则可列方程为( )
A. =-9 B. +2= C. -2= D. =+9
9.已知点M(6,a-3),N(-2,a),P(2,a)在同一个函数图象上,则这个函数图象可能是( )
A. B.
C. D.
10.计算机中常用的十六进制是一种逢16进1的计数制,采用数字0~9和字母A~F共16个计数符号,这些符号与十进制的数字的对应关系如表:
十六进制 0 1 2 3 4 5 6
十进制 0 1 2 3 4 5 6
十六进制 8 9 A B C D E
十进制 8 9 10 11 12 13 14
例如,用十六进制表示D+E=1B,用十进制表示也就是13+14=1×16+11,则用十六进制表示E×F=( )
A. 6E B. 2D C. D2 D. 210
二、填空题:本题共6小题,每小题3分,共18分。
11.分解因式:9x2-3xy= ______.
12.如图,在△ABC中,点D,E分别为边AB,AC上的点,且DE∥BC,若AD=5,BD=10,DE=3,则BC的长为______.
13.设x1,x2是一元一次方程2x2-3x-10=0的两根,=______.
14.某学校广播站要新招1名广播员,甲、乙两名同学经过选拔进入复试环节,参加了口语表达、写作能力两项测试,得分如表:
口语表达 写作能力
甲同学 80 90
乙同学 90 80
该学校规定口语表达按60%、写作能力按40%计入总成绩,根据总成绩从高到低择优录取.通过计算,被录取的同学是______.
15.如图,矩形ABCD两组对边分别和坐标轴平行且矩形的对角线交点为原点,点C在函数的图象上,则矩形ABCD的面积为______.
16.如图1是安装“摩擦铰链”的平开窗,如图2,点C、D、E是窗框AB上的定点,AC=5cm,CD=8cm,DE=26,BE=13cm,转轴H、F分别是窗门底部MN和支架HE上的定点,且HF=AC,滑点P在轨道CD上运动,当点P运动到点C时,窗户关闭(窗门底部MN与面框AB重合):如图3,当窗户开到最大时,点P与D重合,此时∠PFE=90°,PF<EF,则PF= ______cm,此时点N到AB的距离为______cm.
三、解答题:本题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.(本小题8分)
计算:.
18.(本小题8分)
解方程:x2-5x+6=0
19.(本小题8分)
如图,∠A=∠D,AC∥DF,求证:△ABC∽△DEF.
20.(本小题8分)
某校的饮水机有温水、开水两个按钮,温水和开水共用一个出水口.温水的温度为30℃,流速为20ml/s;开水的温度为100℃,流速为15ml/s.某学生先接了一会儿温水,又接了一会儿开水,得到一杯210ml温度为60℃的水(不计热损失),求该学生分别接温水和开水的时间.
物理常识
开水和温水混合时会发生热传递,开水放出的热量等于温水吸收的热量,可以转化为:开水的体积×开水降低的温度=温水的体积×温水升高的温度.
21.(本小题8分)
保护环境,人人有责,某校为培养学生“垃圾分类,从我做起”的环保意识,组织开展“游戏互动”、“趣味问答”、“模拟投放”三项活动(分别以A、B、C来依次表示这三项活动).活动开始前,将A,B,C这三个字母分别写在三张无差别不透明的卡片正面上,洗匀后正面向下放在桌面上,小南同学先从中随机抽取一张卡片放回后洗匀,小晶同学从中再随机抽取一张卡片.
(1)求小南抽到参加“趣味问答”活动的概率;
(2)用列表法或画树状图法,求小南和小晶都抽到参加“趣味问答”活动的概率.
22.(本小题8分)
如图,O是半圆的圆心,直径AB=10cm.
(1)分别在半圆上的取点C和点D,顺次连接各点,构成以A,O,C,D为顶点的菱形,请用直尺和圆规求作符合要求的菱形;
(2)求(1)中菱形的面积.
23.(本小题8分)
【阅读材料】用“割尾法”判断一个三位数能否是7的整数倍.
方法:三位数割掉末位数字c得两位数,再用减去c的2倍所得的差为.若是7的整数倍,则是7的整数倍. 注: 举例:对于三位数364,割掉末位数字4得36,36-4×2=28,因为28是7的整数倍,所以364是7的整数倍.
(1)尝试用“割尾法”判断455能否是7的整数倍.
(2)材料中的判断方法是“若是7的整数倍,则是7的整数倍”,请证明这种方法的正确性.
24.(本小题8分)
如图,在△ABC中,AB=AC,∠BAC=90°,点D是△ABC内一点,且CD=CA.
(1)求证:∠ACD=2∠BAD;
(2)将线段DA绕点D顺时针旋转90°得到线段DE,连接AE交CD于点F.
①依题意补全图形;
②若点F恰是CD的中点,用等式表示AE与BD之间的数量关系,并证明.
25.(本小题8分)
根据背景素材,探索解决问题.
测算拉索桥立柱的高
素材1 一条桥身形状和抛物线y= x2相同的拉索桥,桥的跨径OH的水平距离为22米,点O和点H处于同一水平线.
素材2 (1)桥的两根主立柱AB和GL拉出铁索固定桥身,两个立柱中间共有10根拉索(如图);(2)立柱和铁索与桥身的连接点水平等距分布(即相邻的两个连接点的水平距离相等);(3)经测量拉索AC与水平线CE成45°角,从左侧第3个拉索连接点D射出的探测光线DP交立柱AB于点P,从连接点C射出的探测光线CB交立柱于点B,且DP∥CB.
问题解决
任务1 建立模型 以点O为原点,水平线为x轴,以1米为一个单位长度,建立直角坐标系,根据素材1求桥身模型的函数解析式.
任务2 利用模型 根据任务1所求的解析式模型,分别求点D、C的坐标.
任务3 分析计算 若点P恰好为OB中点,根据素材2及任务1和任务2得到的函数模型和数据,求立柱AB的高度.
1.【答案】B
2.【答案】C
3.【答案】A
4.【答案】D
5.【答案】C
6.【答案】D
7.【答案】B
8.【答案】B
9.【答案】A
10.【答案】C
11.【答案】3x(3x-y)
12.【答案】9
13.【答案】5
14.【答案】乙同学
15.【答案】8
16.【答案】10
17.【答案】.
18.【答案】解:∵x2-5x+6=0,
∴(x-2)(x-3)=0,
则x-2=0或x-3=0,
解得x1=2,x2=3.
19.【答案】证明:∵AC∥DF,
∴∠ACB=∠DFE,
∵∠A=∠D,
∴△ABC∽△DEF.
20.【答案】该学生接温水的时间为6s,接开水的时间为6s.
21.【答案】解(1)依题意知抽到参加“趣味问答”的概率为;
(2)树状图如下:
共有9种等可能的结果,其中小南和小晶都抽到参加“趣味问答”活动的结果有1种,
∴小南和小晶都抽到参加“趣味问答”活动的概率为.
22.【答案】见解析;
cm2.
23.【答案】是,理由见解析; 证明见解析.
24.【答案】见解析过程;
①见解析过程;②AE=2BD,理由见解析过程.
25.【答案】解:(1)如图所示,
∵抛物线经过(0,0),(22,0),
∴抛物线的对称轴为直线x=11,
设抛物线解析式为:y=-,
代入(0,0)得:0=-(0-11)2+k,
解得k=,
∴抛物线解析式为:y=-(x-11)2+;
(2)由题意可知,线段OH被均分成11条相等的线段,每段长为(22÷11=2米),
不妨设点C(10,m),D(6,n),
当x=10时,m=-(10-11)2+=2;
当x=6时,n=-(6-11)2+=;
∴C(10,2),D(6,);
(3)设CE与y轴交于点M,作DN⊥y轴于点N,则DN∥CM∥OH,
∴∠3=∠4,∠1=∠2,∠BMC=∠BND,
∵DP∥BC,
∴∠2=∠4,∠1=∠3,
∴△BMC∽△PND,
∴,
∵DN=6,CM=10,OM=2,ON=,OB=2OP,
∴,
解得OP=2,
∴OB=4,
∵∠ACE=45°,
∴∠ACE=∠CAM,
∴AM=CM=10,
∴AB=AM+OM+OB=10+2+4=16.
故立柱AB的高度为16米.
第1页,共1页
同课章节目录
