3.4力的合成与分解(共45张PPT) 高一上学期物理 人教版(2019) 必修第一册
文档属性
| 名称 | 3.4力的合成与分解(共45张PPT) 高一上学期物理 人教版(2019) 必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-08-24 00:00:00 | ||
图片预览






文档简介
(共45张PPT)
第4节 力的合成与分解
第三章
2019人教版 必修一
新课导入
通过这节课学习我们可知:即使在算正确的情况下也能不等于2
本山大叔你错了
在算错的情况下不等于2
1+1在什么情况下不等于2?
思考:生活中常见到这样的事,一桶水,小孩需要两个才能提起,而大人只需要自己就能很轻松地提起它,就力的作用效果而言,小孩与大人的作用效果是否一样?
等效
两个力的作用效果=一个力的作用效果
G
F1
F2
G
F
今天我们学习力的合成,将接触一种很重要的物理思想方法等效代替
新知讲解
一、合力(resultant force)与分力(component force)
1、定义:
假设一个力单独作用的效果跟某几个力共同作用的 相同,这个力就叫作那几个力的合力。
假设几个力共同作用的效果跟某个力单独作用的效果相同,这几个力就叫作那个力的分力。
合力
分力
等效替代
新知讲解
2、关系:
(1)等效性:合力的作用效果与分力的共同作用效果相同,它们在效果上可以相互替代。
(2)同体性:各个分力是作用在同一物体上的,分力与合力为同一物体,作用在不同物体上的力不能求合力。
(3)瞬时性:各个分力与合力具有瞬时对应关系,某个分力变化了,合力也同时发生变化。
使物体发生相同的形变
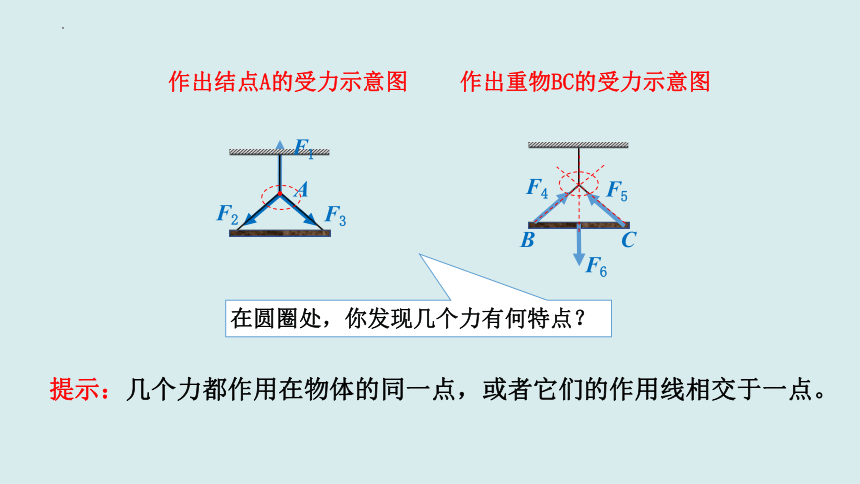
作出结点A的受力示意图
作出重物BC的受力示意图
A
B C
F1
F2
F3
F4
F5
F6
提示:几个力都作用在物体的同一点,或者它们的作用线相交于一点。
在圆圈处,你发现几个力有何特点?
G
F1
F2
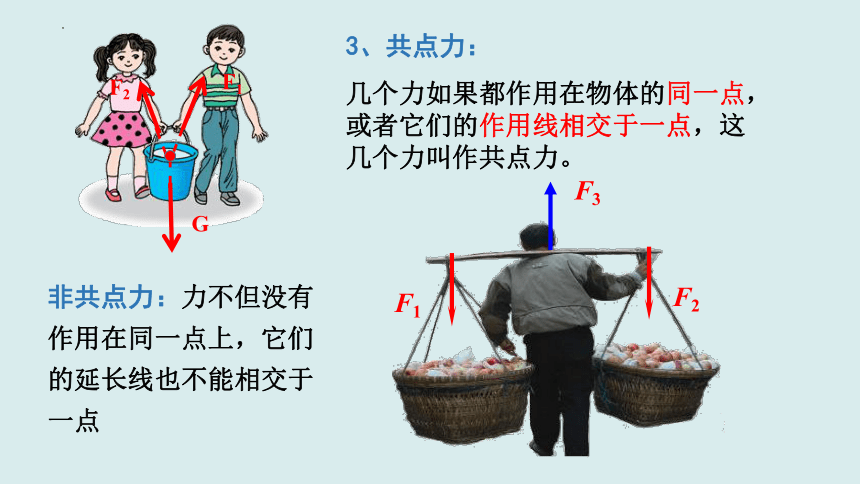
3、共点力:
几个力如果都作用在物体的同一点,或者它们的作用线相交于一点,这几个力叫作共点力。
非共点力:力不但没有作用在同一点上,它们的延长线也不能相交于一点
F1
F2
F3
新知讲解
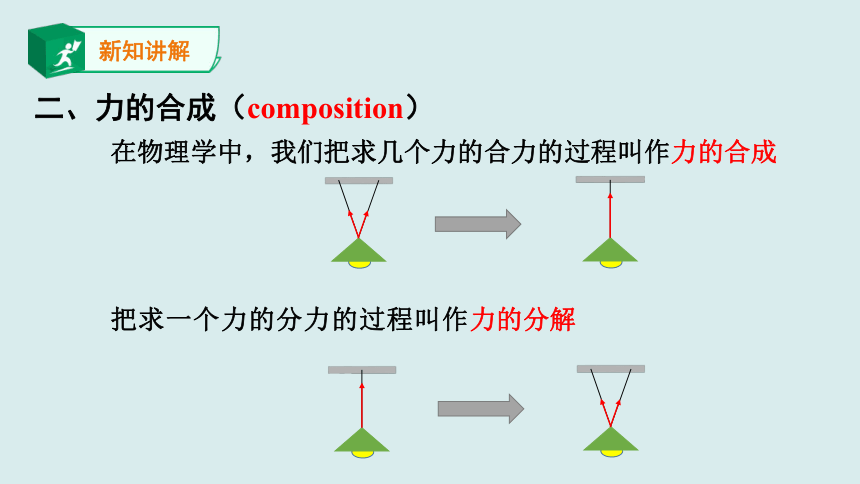
在物理学中,我们把求几个力的合力的过程叫作力的合成
把求一个力的分力的过程叫作力的分解
二、力的合成(composition)
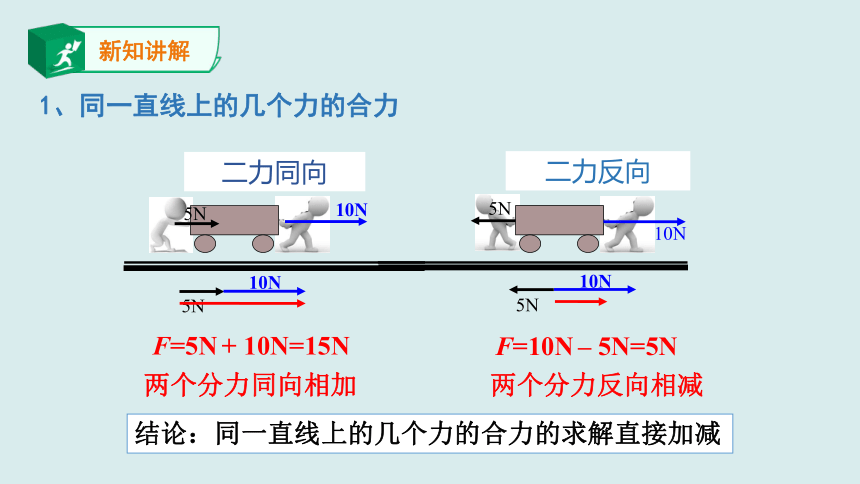
1、同一直线上的几个力的合力
结论:同一直线上的几个力的合力的求解直接加减
二力同向
10N
5N
10N
5N
二力反向
5N
10N
10N
F=5N + 10N=15N
F=10N – 5N=5N
5N
新知讲解
两个分力同向相加
两个分力反向相减
思考
F
F1
F2
如图所示,当F1、F2 互成一定角度时,它们的合力大小还是F1+F2 吗
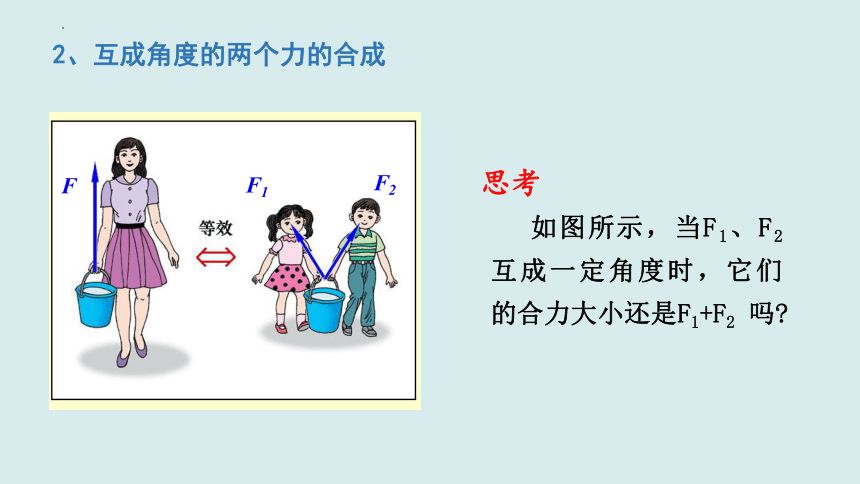
2、互成角度的两个力的合成
探究两个互成角度的力的合成规律
一、实验目的:两个互成角度的力的合成规律
二、思考:
(1)如何测量合力和分力的大小?
(2)如何测量合力和分力的方向?
(3)如何保证合力和分力的效果是相同的?
三、实验器材:弹簧测力计(两只)、橡皮条、细绳套、刻度尺
实验探究
请同学们阅读教材,然后小组讨论,如何利用以上器材设计实验方案?
三、实验探究
1、实验器材
方木板一块、白纸、橡皮筋、弹簧测力计两个、细绳套(两个)、三角板、刻度尺、图钉
2、实验原理
互成角度的共点力F1、F2作用于橡皮筋的结点上,与只用一个力F’作用在结点上,效果相同(等效替代)
(1)在桌上平放一个
木板,在方木板上铺上
一张白纸,用图钉把白
纸固定好。
3、进行实验
(2)用图钉把橡皮筋的一端固定在板上一点,在橡皮筋的另外一端拴上两条细绳套。
3、进行实验
(2)用图钉把橡皮筋的一端固定在板上一点,在橡皮筋的另外一端拴上两条细绳套。
3、进行实验
(2)用图钉把橡皮筋的一端固定在板上一点,在橡皮筋的另外一端拴上两条细绳套。
3、进行实验
(3)用两个弹簧测力计分别钩住绳套,互成角度地拉橡皮筋,使橡皮筋伸长,结点达到某一位置O点
3、进行实验
O
(4)用铅笔记下O的位置和两条细绳的方向,分别读出两只弹簧测力计的示数。
需要记录哪些信息?
注意哪些问题?
3、进行实验
O
(5)只用一只弹簧测力计,通过细绳把橡皮筋的结点拉到相同的位置O点。
需要记录哪些信息?
注意哪些问题?
3、进行实验
(6)按照一定标度,用铅笔和刻度尺作出两个分力F1、F2及合力F的图示。
F1
F2
3、进行实验
1.位置不变:在同一次实验中,使橡皮条拉长时结点的位置一定要相同.
2.角度合适:用两个弹簧测力计钩住细绳套互成角度地拉橡皮条时,其夹角不宜太小,也不宜太大。
3. 与木板平行:拉橡皮筋时要使弹簧称与木板平面平行。
4.尽量减少误差
(1)在合力不超出量程及橡皮条弹性限度内的前提下,测量数据应尽量大一些.
(2)细绳套应适当长一些,便于确定力的方向.不要直接沿细绳套方向画直线,应在细绳套两端画个投影点,去掉细绳套后,连直线确定力的方向.
5.统一标度:在同一次实验中,画力的图示选定的标度要相同,并且要恰当选定标度,使力的图示稍大一些。
注意事项
F2
F合
·
F1
O
互成角度的两个力合成时,不是简单的将两个力相加减,而是用两个共点力F1和F2为邻边作平行四边形,那么合力F的大小和方向就可以用这两邻边之间的对角线表示,称为平行四边形定则
4、实验结论
注意:力用实线,辅助线用虚线!
也适用于位移、速度、加速度等矢量的合成。
新知讲解
3、平行四边形定则
以表示这两个力的有向线段为邻边作平行四边形,这两个邻边之间的对角线就代表合力的大小和方向 ,这个规律叫做平行四边形定则
矢量运算法则
大小:标度
方向:角度
合力大小的范围:
|F1-F2|≤F≤|F1+F2|
F
θ
F1
F2
o
F1
F2
F3
F4
F12
F123
F1234
先求出任意两个力的合力,再求出这个合力跟第三个力的合力,直到把所有的力都合成进去,最后得到的结果就是这些力的合力
逐次合成法
4、多个力的合成
新知讲解
5、三角形定则
F1
F2
F
θ
F
θ
o
三角形定则
共起点
首尾相接
F1
F2
平行四边形的邻边平移后,两个共点力首尾相接,从一个力的始端指向另一个力的末端,这个有向线段就是合力。
新知讲解
物体受三个力处于平衡态:平移后构成封闭矢量三角形
F1
F2
F4
F3
F
G
N
T
F=0
F3
F1
F2
F4
F5
5、三角形定则
新知讲解
F1
F2
F3
F4
F2
F3
F4
F1234
合力一定大于分力吗?
6、多边形定则
新知讲解
1.两个分力F1、F2大小不变,合力随夹角如何变化?
①合力最大: F=F1+F2(夹角为0 , 即方向相同)
②合力最小: F=︱F1 - F2︱(夹角为180 ,即方向相反)
q
F
③合力的大小范围: ︱F1 - F2︱ ≤ F ≤ F1 + F2
④合力可能大于、等于、小于任一分力
⑤两个分力F1、F2大小不变,两个分力的夹角越大,合力越小。
思考讨论1
①合力一定时,两等大分力大小随夹角增大而增大
②当夹角为120°时,合力F=F1=F2
2.合力一定时,两等大分力随夹角如何变化?
思考讨论2
F2
F1
F合
F2
F合
①两分力反向时
②两分力成钝角时
③两分力成锐角时
F合
一个分力不变,另一个分力增大时,合力可能增大,可能减小,可能不变
3.一个分力不变,另一个分力增大时,合力一定增大吗?
思考讨论3
②任取两个力,求出其合力的范围;
如果第三个力在这个范围之内,
则三个力的合力最小值为零;
如果第三个力不在这个范围内,
则合力最小值等于最大的力减去另外两个力之和。
F3
F2
F1
F12
F123
4.三个共点力合成后的范围?
①三个力共线且同向时,其合力最大,等于F1+F2+F3
思考讨论4
F
力的分解是力的合成的逆运算,因此也遵循平行四边形定则。
如果没有其它限制,对于同一条对角线,可以作出无数个不同的平行四边形,那么该怎么分解呢?
三、力的分解(resolution of force)
新知讲解
1、按力的效果分解
两个静止在斜面上的物体,重力都为G,产生的作用效果相同吗?
G1
G1
G2
G2
G
G
①压挡板 ②压斜面
①压挡板 ②压斜面
q
q
2、在限定条件下力的分解
①已知两分力的方向
F
F1
F2
有唯一组解
②已知一个分力的大小和方向
F
F2
有唯一组解
F
F1
F2
F1
O1
O2
F2
F1+F2F
F1
F2
F1
O1
O2
F2
F1+F2=F 一解
③已知两个分力的大小
F
F1
F2
F1
O1
O2
F2
F1
F2
F1+F2>F 两组解(平面内)
无数组解(三维空间内)
④已知F1的方向和F2的大小
o
F
F2a
F1a
F1c
F2c
F2b
F1b
F2d
F1d
F2=Fsinθ 一个解
FsinθF≤ F2 一个解
力的分解的步骤:
(1)分析力的作用效果;
(2)据力的作用效果定分力的方向;(画两个分力的方向)
(3)用平行四边形定则定分力的大小;
(4)据数学知识求分力的大小和方向。
1.力的正交分解:将力沿两互相垂的方向分解
Fx
Fy
Fy=F·sinθ
x方向的分力:
Fx =F·cosθ
0
x
y
y方向的分力:
θ
F
为什么要正交分解呢?
三、力的正交分解
新知讲解
化复杂的矢量运算为普通的代数运算,将力的合成化简为同向或反向或垂直方向。便于运用普通代数运算公式来解决矢量的运算。
2.正交分解的目的
正交分解法求合力,运用了“欲合先分”的策略,即为了合成而分解,降低了运算的难度,是一种重要思想方法。
3.正交分解的基本思想
分解时最好兼顾力的实际效果
新知讲解
F1
F2
x
y
O
F2y
F1y
F1x
F2X
(2)将不在坐标轴上的力分解到坐标轴上;
(1)建立xoy直角坐标系
F1X=F1cosθ1
F1y=F1sinθ1
F2X=F2cosθ2
F2y=F2sinθ2
F1
F2
θ1
θ2
4.正交分解的步骤
新知讲解
(3)分别求出x轴、y轴上各分力的矢量和,即
Fx=F1x+F2x+……
Fy=F1y+F2y+……
(4)求共点力的合力:
与x轴正方向的夹角为θ
x
y
o
FX
Fy
F
θ
大小:
方向:
新知讲解
F拉
θ
x
y
G
f静
N
o
F2
F1
θ
O
x
y
v
G
F
N
f滑
5、正交分解的常见模型
标量:在物理学中,只有大小而没有方向的物理量叫标量。
标量运算遵循算术加减法法则(代数运算法则)1+1=2。
矢量:在物理学中,既有大小又有方向的物理量叫矢量。
四、矢量与标量
如:位移,力,速度等等
如:时间,路程,质量,温度,长度,能量等等
矢量运算法则:平行四边形法则
课 堂 小 结
合力
分力
思想:等效替代
运算法则:平行四边形定则
力的合成
力的分解
第4节 力的合成与分解
第三章
2019人教版 必修一
新课导入
通过这节课学习我们可知:即使在算正确的情况下也能不等于2
本山大叔你错了
在算错的情况下不等于2
1+1在什么情况下不等于2?
思考:生活中常见到这样的事,一桶水,小孩需要两个才能提起,而大人只需要自己就能很轻松地提起它,就力的作用效果而言,小孩与大人的作用效果是否一样?
等效
两个力的作用效果=一个力的作用效果
G
F1
F2
G
F
今天我们学习力的合成,将接触一种很重要的物理思想方法等效代替
新知讲解
一、合力(resultant force)与分力(component force)
1、定义:
假设一个力单独作用的效果跟某几个力共同作用的 相同,这个力就叫作那几个力的合力。
假设几个力共同作用的效果跟某个力单独作用的效果相同,这几个力就叫作那个力的分力。
合力
分力
等效替代
新知讲解
2、关系:
(1)等效性:合力的作用效果与分力的共同作用效果相同,它们在效果上可以相互替代。
(2)同体性:各个分力是作用在同一物体上的,分力与合力为同一物体,作用在不同物体上的力不能求合力。
(3)瞬时性:各个分力与合力具有瞬时对应关系,某个分力变化了,合力也同时发生变化。
使物体发生相同的形变
作出结点A的受力示意图
作出重物BC的受力示意图
A
B C
F1
F2
F3
F4
F5
F6
提示:几个力都作用在物体的同一点,或者它们的作用线相交于一点。
在圆圈处,你发现几个力有何特点?
G
F1
F2
3、共点力:
几个力如果都作用在物体的同一点,或者它们的作用线相交于一点,这几个力叫作共点力。
非共点力:力不但没有作用在同一点上,它们的延长线也不能相交于一点
F1
F2
F3
新知讲解
在物理学中,我们把求几个力的合力的过程叫作力的合成
把求一个力的分力的过程叫作力的分解
二、力的合成(composition)
1、同一直线上的几个力的合力
结论:同一直线上的几个力的合力的求解直接加减
二力同向
10N
5N
10N
5N
二力反向
5N
10N
10N
F=5N + 10N=15N
F=10N – 5N=5N
5N
新知讲解
两个分力同向相加
两个分力反向相减
思考
F
F1
F2
如图所示,当F1、F2 互成一定角度时,它们的合力大小还是F1+F2 吗
2、互成角度的两个力的合成
探究两个互成角度的力的合成规律
一、实验目的:两个互成角度的力的合成规律
二、思考:
(1)如何测量合力和分力的大小?
(2)如何测量合力和分力的方向?
(3)如何保证合力和分力的效果是相同的?
三、实验器材:弹簧测力计(两只)、橡皮条、细绳套、刻度尺
实验探究
请同学们阅读教材,然后小组讨论,如何利用以上器材设计实验方案?
三、实验探究
1、实验器材
方木板一块、白纸、橡皮筋、弹簧测力计两个、细绳套(两个)、三角板、刻度尺、图钉
2、实验原理
互成角度的共点力F1、F2作用于橡皮筋的结点上,与只用一个力F’作用在结点上,效果相同(等效替代)
(1)在桌上平放一个
木板,在方木板上铺上
一张白纸,用图钉把白
纸固定好。
3、进行实验
(2)用图钉把橡皮筋的一端固定在板上一点,在橡皮筋的另外一端拴上两条细绳套。
3、进行实验
(2)用图钉把橡皮筋的一端固定在板上一点,在橡皮筋的另外一端拴上两条细绳套。
3、进行实验
(2)用图钉把橡皮筋的一端固定在板上一点,在橡皮筋的另外一端拴上两条细绳套。
3、进行实验
(3)用两个弹簧测力计分别钩住绳套,互成角度地拉橡皮筋,使橡皮筋伸长,结点达到某一位置O点
3、进行实验
O
(4)用铅笔记下O的位置和两条细绳的方向,分别读出两只弹簧测力计的示数。
需要记录哪些信息?
注意哪些问题?
3、进行实验
O
(5)只用一只弹簧测力计,通过细绳把橡皮筋的结点拉到相同的位置O点。
需要记录哪些信息?
注意哪些问题?
3、进行实验
(6)按照一定标度,用铅笔和刻度尺作出两个分力F1、F2及合力F的图示。
F1
F2
3、进行实验
1.位置不变:在同一次实验中,使橡皮条拉长时结点的位置一定要相同.
2.角度合适:用两个弹簧测力计钩住细绳套互成角度地拉橡皮条时,其夹角不宜太小,也不宜太大。
3. 与木板平行:拉橡皮筋时要使弹簧称与木板平面平行。
4.尽量减少误差
(1)在合力不超出量程及橡皮条弹性限度内的前提下,测量数据应尽量大一些.
(2)细绳套应适当长一些,便于确定力的方向.不要直接沿细绳套方向画直线,应在细绳套两端画个投影点,去掉细绳套后,连直线确定力的方向.
5.统一标度:在同一次实验中,画力的图示选定的标度要相同,并且要恰当选定标度,使力的图示稍大一些。
注意事项
F2
F合
·
F1
O
互成角度的两个力合成时,不是简单的将两个力相加减,而是用两个共点力F1和F2为邻边作平行四边形,那么合力F的大小和方向就可以用这两邻边之间的对角线表示,称为平行四边形定则
4、实验结论
注意:力用实线,辅助线用虚线!
也适用于位移、速度、加速度等矢量的合成。
新知讲解
3、平行四边形定则
以表示这两个力的有向线段为邻边作平行四边形,这两个邻边之间的对角线就代表合力的大小和方向 ,这个规律叫做平行四边形定则
矢量运算法则
大小:标度
方向:角度
合力大小的范围:
|F1-F2|≤F≤|F1+F2|
F
θ
F1
F2
o
F1
F2
F3
F4
F12
F123
F1234
先求出任意两个力的合力,再求出这个合力跟第三个力的合力,直到把所有的力都合成进去,最后得到的结果就是这些力的合力
逐次合成法
4、多个力的合成
新知讲解
5、三角形定则
F1
F2
F
θ
F
θ
o
三角形定则
共起点
首尾相接
F1
F2
平行四边形的邻边平移后,两个共点力首尾相接,从一个力的始端指向另一个力的末端,这个有向线段就是合力。
新知讲解
物体受三个力处于平衡态:平移后构成封闭矢量三角形
F1
F2
F4
F3
F
G
N
T
F=0
F3
F1
F2
F4
F5
5、三角形定则
新知讲解
F1
F2
F3
F4
F2
F3
F4
F1234
合力一定大于分力吗?
6、多边形定则
新知讲解
1.两个分力F1、F2大小不变,合力随夹角如何变化?
①合力最大: F=F1+F2(夹角为0 , 即方向相同)
②合力最小: F=︱F1 - F2︱(夹角为180 ,即方向相反)
q
F
③合力的大小范围: ︱F1 - F2︱ ≤ F ≤ F1 + F2
④合力可能大于、等于、小于任一分力
⑤两个分力F1、F2大小不变,两个分力的夹角越大,合力越小。
思考讨论1
①合力一定时,两等大分力大小随夹角增大而增大
②当夹角为120°时,合力F=F1=F2
2.合力一定时,两等大分力随夹角如何变化?
思考讨论2
F2
F1
F合
F2
F合
①两分力反向时
②两分力成钝角时
③两分力成锐角时
F合
一个分力不变,另一个分力增大时,合力可能增大,可能减小,可能不变
3.一个分力不变,另一个分力增大时,合力一定增大吗?
思考讨论3
②任取两个力,求出其合力的范围;
如果第三个力在这个范围之内,
则三个力的合力最小值为零;
如果第三个力不在这个范围内,
则合力最小值等于最大的力减去另外两个力之和。
F3
F2
F1
F12
F123
4.三个共点力合成后的范围?
①三个力共线且同向时,其合力最大,等于F1+F2+F3
思考讨论4
F
力的分解是力的合成的逆运算,因此也遵循平行四边形定则。
如果没有其它限制,对于同一条对角线,可以作出无数个不同的平行四边形,那么该怎么分解呢?
三、力的分解(resolution of force)
新知讲解
1、按力的效果分解
两个静止在斜面上的物体,重力都为G,产生的作用效果相同吗?
G1
G1
G2
G2
G
G
①压挡板 ②压斜面
①压挡板 ②压斜面
q
q
2、在限定条件下力的分解
①已知两分力的方向
F
F1
F2
有唯一组解
②已知一个分力的大小和方向
F
F2
有唯一组解
F
F1
F2
F1
O1
O2
F2
F1+F2
F1
F2
F1
O1
O2
F2
F1+F2=F 一解
③已知两个分力的大小
F
F1
F2
F1
O1
O2
F2
F1
F2
F1+F2>F 两组解(平面内)
无数组解(三维空间内)
④已知F1的方向和F2的大小
o
F
F2a
F1a
F1c
F2c
F2b
F1b
F2d
F1d
F2=Fsinθ 一个解
Fsinθ
力的分解的步骤:
(1)分析力的作用效果;
(2)据力的作用效果定分力的方向;(画两个分力的方向)
(3)用平行四边形定则定分力的大小;
(4)据数学知识求分力的大小和方向。
1.力的正交分解:将力沿两互相垂的方向分解
Fx
Fy
Fy=F·sinθ
x方向的分力:
Fx =F·cosθ
0
x
y
y方向的分力:
θ
F
为什么要正交分解呢?
三、力的正交分解
新知讲解
化复杂的矢量运算为普通的代数运算,将力的合成化简为同向或反向或垂直方向。便于运用普通代数运算公式来解决矢量的运算。
2.正交分解的目的
正交分解法求合力,运用了“欲合先分”的策略,即为了合成而分解,降低了运算的难度,是一种重要思想方法。
3.正交分解的基本思想
分解时最好兼顾力的实际效果
新知讲解
F1
F2
x
y
O
F2y
F1y
F1x
F2X
(2)将不在坐标轴上的力分解到坐标轴上;
(1)建立xoy直角坐标系
F1X=F1cosθ1
F1y=F1sinθ1
F2X=F2cosθ2
F2y=F2sinθ2
F1
F2
θ1
θ2
4.正交分解的步骤
新知讲解
(3)分别求出x轴、y轴上各分力的矢量和,即
Fx=F1x+F2x+……
Fy=F1y+F2y+……
(4)求共点力的合力:
与x轴正方向的夹角为θ
x
y
o
FX
Fy
F
θ
大小:
方向:
新知讲解
F拉
θ
x
y
G
f静
N
o
F2
F1
θ
O
x
y
v
G
F
N
f滑
5、正交分解的常见模型
标量:在物理学中,只有大小而没有方向的物理量叫标量。
标量运算遵循算术加减法法则(代数运算法则)1+1=2。
矢量:在物理学中,既有大小又有方向的物理量叫矢量。
四、矢量与标量
如:位移,力,速度等等
如:时间,路程,质量,温度,长度,能量等等
矢量运算法则:平行四边形法则
课 堂 小 结
合力
分力
思想:等效替代
运算法则:平行四边形定则
力的合成
力的分解
