1.4 绝对值(共14张PPT) 2025-2026学年数学华东师大版(2024)七年级上册
文档属性
| 名称 | 1.4 绝对值(共14张PPT) 2025-2026学年数学华东师大版(2024)七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-23 00:00:00 | ||
图片预览





文档简介
1.4绝对值
1.理解绝对值的概念及其几何意义;
2.会求一个数的绝对值,会求绝对值已知的数;
3.了解绝对值的非负性,并能用其非负性解决相关问题.
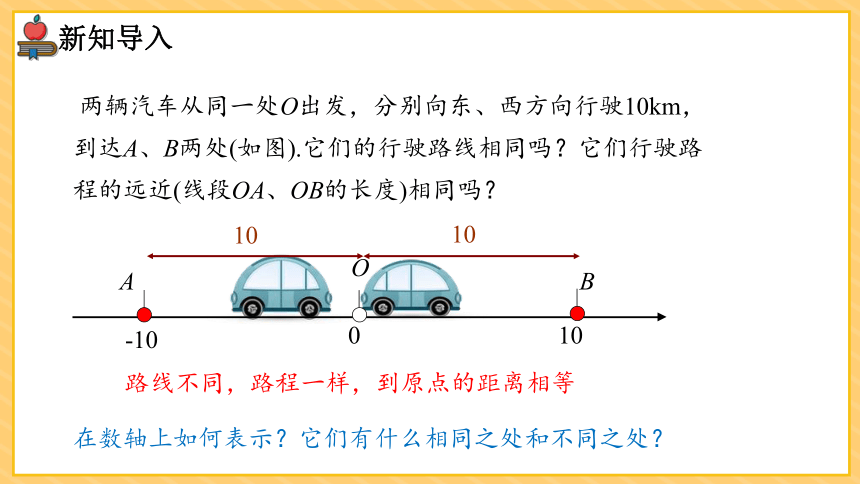
两辆汽车从同一处O出发,分别向东、西方向行驶10km,到达A、B两处(如图).它们的行驶路线相同吗?它们行驶路程的远近(线段OA、OB的长度)相同吗?
A
O
B
10
10
-10
0
10
路线不同,路程一样,到原点的距离相等
在数轴上如何表示?它们有什么相同之处和不同之处?
-10与10在数轴上所表示的点到原点的距离都是10个单位长度,它们的符号不同.
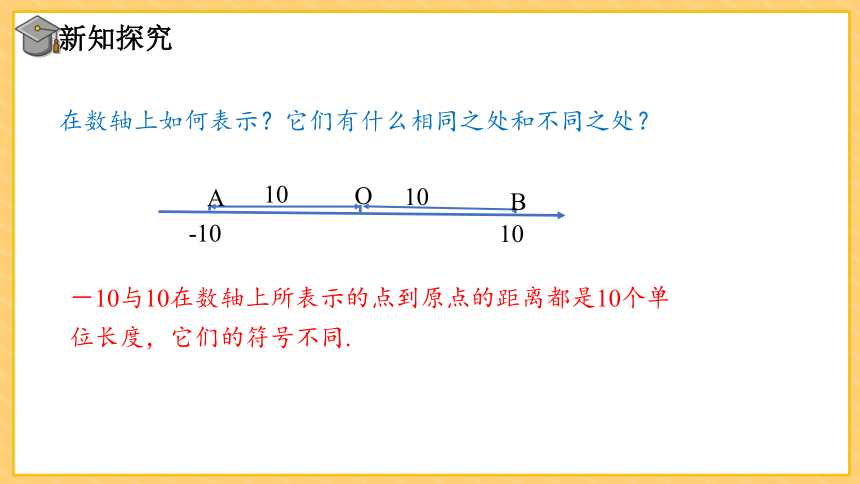
在数轴上如何表示?它们有什么相同之处和不同之处?
O
10
-10
10
10
A
B
-10与10在数轴上所表示的点到原点的距离都是10个单位长度,它们的符号不同.
例如,在数轴上表示+5的点与原点的距离是5,所以+5的绝对值是5,记作|+5|=5;在数轴上表示-6的点与原点的距离是6,所以-6的绝对值是6,记作|-6|=6.
我们把在数轴上表示数a的点与原点的距离叫做数a的绝对值,记作|a|.
概念
(1)|+2|=______,|15|=______,|+8.2|=______;
(2)|0|=______;
(3)|-3|=______;|-0.2|=______;|-8.2|=______.
?
2
8.2
0
3
0.2
8.2
试一试
怎样求一个数的绝对值?从这些结果中你能发现什么规律?
可以将表示这些数的点在数轴上表示出来,根据各点到原点的距离,就可以求得该点表示的数的绝对值.
方法
1.一个正数的绝对值是它本身
2.0的绝对值是0
3.一个负数的绝对值是它的相反数
归纳
4.一个数的绝对值就是表示这个数的点到原点的距离,离原点越远,绝对值越大;离原点越近,绝对值越小
1.当a>0时,|a|=______;
2.当a=0时,|a|=______;
3.当a<0时,|a|=______.
a
0
-a
任何一个有理数的绝对值总是正数或0(通常也称非负数)
即对任何有理数a,总有 |a|≥0. (绝对值具有非负性)
你能将前面的结论用数学式子表示吗?
试一试
归纳
例1 求下列各数的绝对值:
-152,+110,-4.75,10.5.
?
解:?152=152,+110=110,
?4.75=4.75,10.5=10.5.
?
例2 化简:
(1)|-(+12)|; (2)-|-113|.
?
解:(1)?(+12)=?12=12;
(2)-?113=?113.
?
化简含绝对值符号的式子时,要先求绝对值,再按照双重符号化简规则进行化简.
1.数轴上,在原点左侧且到原点的距离为3个单位长度的点表示的数是 ( )
A.3 B.-3 C. 13 D.-13
?
B
2.若a是有理数,则下列各式一定为正数的是( )
A.a B.a+1
C.|a| D.|a|+1
D
3.化简:
(1)-| +2.5| ; (2)-|- 3. 4| ; (3)+|-4|; (4)|-(-3)|.
解:(1)原式=-2.5.
(2)原式=-3.4.
(3)原式=4.
(4)原式=|3|=3.
绝对值
概念:数轴上表示数a的点与原点的距离叫做数a的绝对值
绝对值的性质
(1) |a|≥0;
(2)
|a|=a (a>0)
|a|=-a (a<0)
|a|=0 (a=0)
|a|
1.理解绝对值的概念及其几何意义;
2.会求一个数的绝对值,会求绝对值已知的数;
3.了解绝对值的非负性,并能用其非负性解决相关问题.
两辆汽车从同一处O出发,分别向东、西方向行驶10km,到达A、B两处(如图).它们的行驶路线相同吗?它们行驶路程的远近(线段OA、OB的长度)相同吗?
A
O
B
10
10
-10
0
10
路线不同,路程一样,到原点的距离相等
在数轴上如何表示?它们有什么相同之处和不同之处?
-10与10在数轴上所表示的点到原点的距离都是10个单位长度,它们的符号不同.
在数轴上如何表示?它们有什么相同之处和不同之处?
O
10
-10
10
10
A
B
-10与10在数轴上所表示的点到原点的距离都是10个单位长度,它们的符号不同.
例如,在数轴上表示+5的点与原点的距离是5,所以+5的绝对值是5,记作|+5|=5;在数轴上表示-6的点与原点的距离是6,所以-6的绝对值是6,记作|-6|=6.
我们把在数轴上表示数a的点与原点的距离叫做数a的绝对值,记作|a|.
概念
(1)|+2|=______,|15|=______,|+8.2|=______;
(2)|0|=______;
(3)|-3|=______;|-0.2|=______;|-8.2|=______.
?
2
8.2
0
3
0.2
8.2
试一试
怎样求一个数的绝对值?从这些结果中你能发现什么规律?
可以将表示这些数的点在数轴上表示出来,根据各点到原点的距离,就可以求得该点表示的数的绝对值.
方法
1.一个正数的绝对值是它本身
2.0的绝对值是0
3.一个负数的绝对值是它的相反数
归纳
4.一个数的绝对值就是表示这个数的点到原点的距离,离原点越远,绝对值越大;离原点越近,绝对值越小
1.当a>0时,|a|=______;
2.当a=0时,|a|=______;
3.当a<0时,|a|=______.
a
0
-a
任何一个有理数的绝对值总是正数或0(通常也称非负数)
即对任何有理数a,总有 |a|≥0. (绝对值具有非负性)
你能将前面的结论用数学式子表示吗?
试一试
归纳
例1 求下列各数的绝对值:
-152,+110,-4.75,10.5.
?
解:?152=152,+110=110,
?4.75=4.75,10.5=10.5.
?
例2 化简:
(1)|-(+12)|; (2)-|-113|.
?
解:(1)?(+12)=?12=12;
(2)-?113=?113.
?
化简含绝对值符号的式子时,要先求绝对值,再按照双重符号化简规则进行化简.
1.数轴上,在原点左侧且到原点的距离为3个单位长度的点表示的数是 ( )
A.3 B.-3 C. 13 D.-13
?
B
2.若a是有理数,则下列各式一定为正数的是( )
A.a B.a+1
C.|a| D.|a|+1
D
3.化简:
(1)-| +2.5| ; (2)-|- 3. 4| ; (3)+|-4|; (4)|-(-3)|.
解:(1)原式=-2.5.
(2)原式=-3.4.
(3)原式=4.
(4)原式=|3|=3.
绝对值
概念:数轴上表示数a的点与原点的距离叫做数a的绝对值
绝对值的性质
(1) |a|≥0;
(2)
|a|=a (a>0)
|a|=-a (a<0)
|a|=0 (a=0)
|a|
同课章节目录
