1.6 有理数的加法(共31张PPT)2025-2026学年数学华东师大版(2024)七年级上册
文档属性
| 名称 | 1.6 有理数的加法(共31张PPT)2025-2026学年数学华东师大版(2024)七年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-23 23:32:16 | ||
图片预览








文档简介
(共31张PPT)
1.6 有理数的加法
1.6.1有理数的加法法则
1.了解有理数加法的意义,理解有理数加法法则的合理性
2.能运用有理数加法法则进行有理数的加法运算
填空
(1)一个有理数由_______和________两部分组成.
(2)若向东走20米记作20米,则向西走30米记作_________.
(3)若水位升高5米记作5米,则-5米表示________________
(4)小兰向西走了-8米,8米表示__________________________.
符号
绝对值
-30米
水位下降5米
小兰向东走了8米
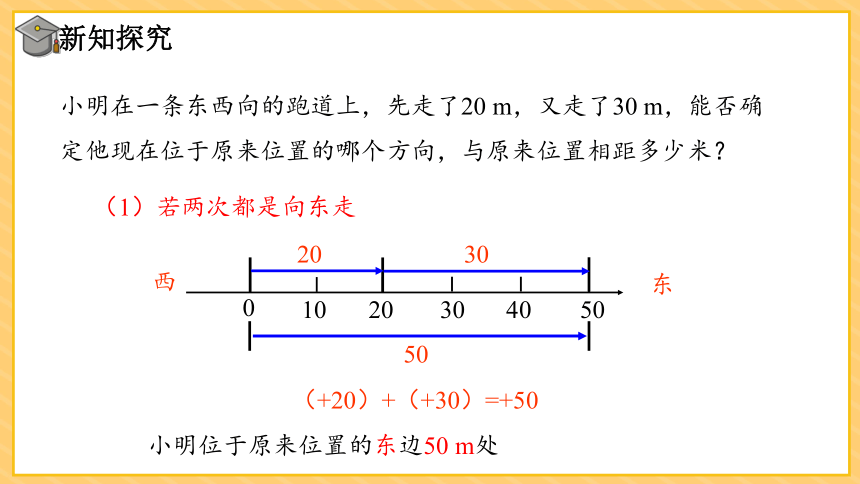
小明在一条东西向的跑道上,先走了20 m,又走了30 m,能否确定他现在位于原来位置的哪个方向,与原来位置相距多少米?
小明最后的位置与行走方向有关,不妨规定向东为正,向西为负.
(1)若两次都是向东走
0
10
20
30
40
50
20
30
50
(+20)+(+30)=+50
东
西
小明位于原来位置的东边50 m处
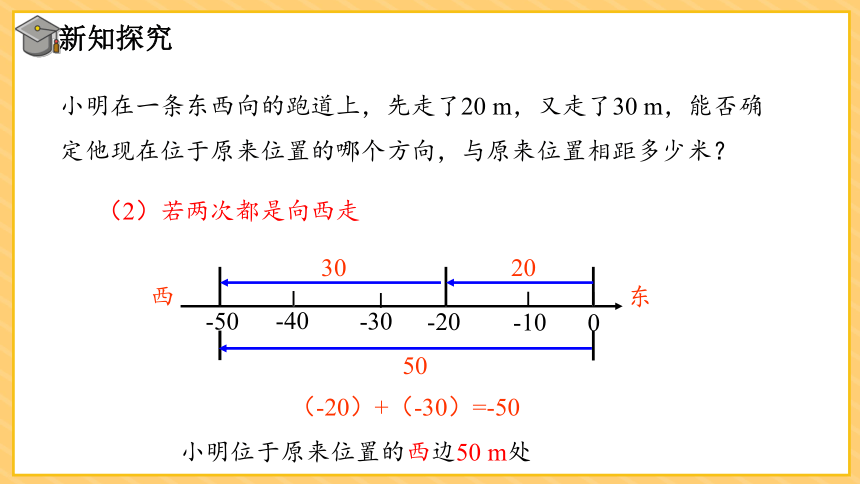
小明在一条东西向的跑道上,先走了20 m,又走了30 m,能否确定他现在位于原来位置的哪个方向,与原来位置相距多少米?
(2)若两次都是向西走
-10
0
-20
-30
-40
-50
20
30
50
(-20)+(-30)=-50
东
西
小明位于原来位置的西边50 m处
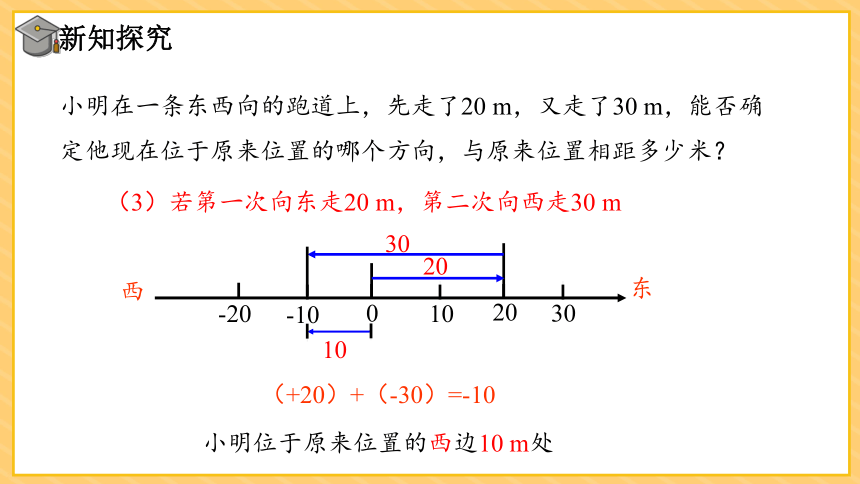
小明在一条东西向的跑道上,先走了20 m,又走了30 m,能否确定他现在位于原来位置的哪个方向,与原来位置相距多少米?
(3)若第一次向东走20 m,第二次向西走30 m
东
-10
10
30
20
-20
0
20
30
10
(+20)+(-30)=-10
西
小明位于原来位置的西边10 m处
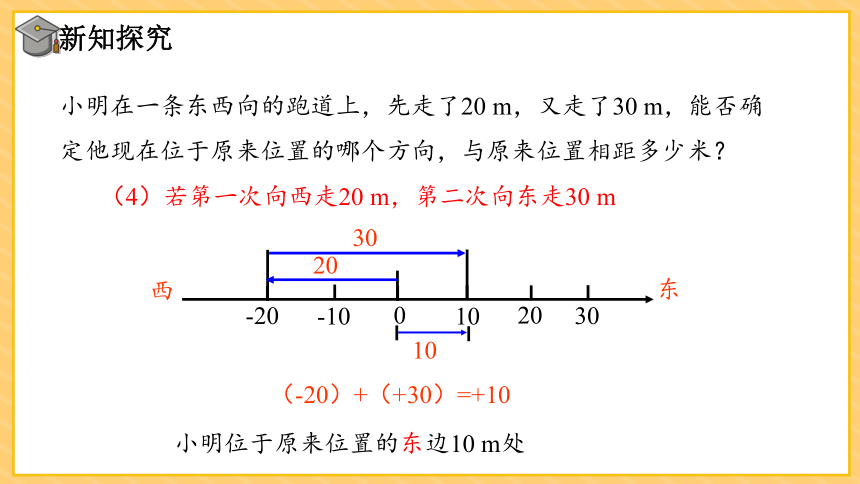
小明在一条东西向的跑道上,先走了20 m,又走了30 m,能否确定他现在位于原来位置的哪个方向,与原来位置相距多少米?
(4)若第一次向西走20 m,第二次向东走30 m
东
-10
10
30
20
-20
0
20
30
10
(-20)+(+30)=+10
西
小明位于原来位置的东边10 m处
小明在一条东西向的跑道上,先走了20 m,又走了30 m,能否确定他现在位于原来位置的哪个方向,与原来位置相距多少米?
(3)(4)两种情形中两个加数的正负号不同(通常可称为异号),让我们再试几次(下列算式中各个加数的正负号和绝对值仍分别表示运动的方向和路程):
(+4) +(-3)=( ), (+3) + (-10)=( ),
(-5) +(+7)=( ), (-6) +2 =( ).
+1
-7
+2
-4
(3)若第一次向东走20 m,第二次向西走30 m:(+20)+(-30)=-10
(4)若第一次向西走20 m,第二次向东走30 m:(-20)+(+30)=+10
还有两种特殊情形:
(5)若第一次向西走了30 m,第二次向东走了30 m,写成
算式是(-30)+(+30)=( ).
(6)若第一次向西走了30 m,第二次没走,写成算式是
(-30)+0=( ).
0
-30
从(1)~(6)所写出的算式中,你能总结出一些规律吗?
1.同号两数相加,取与加数相同的正负号,并把绝对值相加;
2.绝对值不相等的异号两数相加,取绝对值较大的加数的正负号,
并用较大的绝对值减去较小的绝对值;
3.互为相反数的两个数相加得0;
4.一个数与0相加,仍得这个数.
有理数的加法法则:
归纳
绝对值不相等的异号两数相加
互为相反数的两数相加
同号两数相加
绝对值不相等的异号两数相加
例1 计算:
(1)(+2)+(-11); (2)(-12)+(+12);
(3)(-)+(-); (4)(-3.4)+4.3 .
解:(1)(+2)+ (-11)=-(11-2)=-9.
(2) (-12) +(+12)=0.
(3)(-)+(-)=-(+)=-1;
(4)(-3.4)+4.3=+(4.3-3.4)=0.9.
1.如果两个数的和为正数,那么下列描述中,一定错误的是( )
A. 两个数均为正数
B. 两个数一个是正数,另一个是零
C. 两数一正一负,正数比负数的绝对值大
D. 两数一正一负,正数比负数的绝对值小
D
2. 计算:
(1) (-0.6)+(-2.7); (2) 3.7+(-8.4);
(3) 0+(-5.8); (4) 2025+(-2025).
解:(1) (-0.6)+(-2.7)=-(0.6+2.7)=-3.3
(2) 3.7+(-8.4)=-(8.4-3.7)=-4.7
(3) 0+(-5.8)=-5.8
(4) 2025+(-2025)=0
3.用“﹥”或“﹤”符号填空
(1)如果a>0,b>0,那么a+b____0;
(2) 如果a<0,b<0,那么a+b____0;
(3) 如果a>0,b<0,|a|>|b|,那么a+b____0;
(4) 如果a>0,b<0,|a|<|b|,那么a+b____0;
>
<
>
<
1.6.2有理数加法的运算律
1.理解加法交换律、结合律,并能运用字母表示运算律的内容
2.灵活熟练地运用加法交换律、结合律简化运算,并能运用加法运算律解决实际问题.
小学里我们学过的加法运算定律有哪些?举例说明.
引进了负数以后,这些运算律是否还成立呢?
也就是说,上面两个等式中,将5、3.5和2. 5换成任
意的有理数,是否仍然成立呢?
(1)a+b=b+a
(2)(a+b)+c=a+(b+c)
加法交换律 、加法结合律
5 +3.5 = 3.5+5
(5+3.5)+ 2.5 = 5 +(3.5+2.5)
(1) 任意选择两个有理数(至少有一个是负数),分别填入下列□和〇内,并比较两个运算结果:
□+〇和〇+□;
(2) 任意选择三个有理数(至少有一个是负数),分别填入下列□、〇和 内,并比较两个运算结果:
(□+〇)+ 和□+(〇+ ).
你能发现什么?
如:(1)(-30)+20= (2)20 +(-30)=
(3)8+(-5)= (4)(-5)+8=
(5)[8+(-5)]+(-4)= (6) 8+[(-5)+(-4)]=
-10
-10
3
3
-1
-1
有理数的加法仍满足交换律和结合律.
加法交换律:两个数相加,交换加数的位置,和不变.
a+b=b+a.
加法结合律:三个数相加,先把前两个数相加,或者先把后两个数相加,和不变 .(a+b)+c=a+(b+c).
归纳
解:(1) (+26) + (-18) + 5 + (-16)
=(26 + 5) +[(-18) + (-16)]
= 31 + (-34)
=-(34 - 31)
符号相同
例1 计算:(1) (+26) + (-18) + 5 + (-16);
=-3.
(2) (-1.75) + 1.5 + (+7.3) + (-2.25) + (-8.5).
解:(-1.75) + 1.5 + (+7.3) + (-2.25) + (-8.5)
=[(-1.75) + (-2.25)] + [1.5 + (-8.5)] + 7.3
= (-4) + (-7) + 7.3
=(-4) + 0.3
结果是整数
= (-4) + [(-7) + 7.3]
=-3.7.
整数部分相同
例2 10筐苹果,以每筐30千克为基准,超过的千克数记作正数,不足的千克数记作负数,记录如下:
2, -4, 2.5, 3, -0.5, 1.5, 3, -1, 0, -2.5.
问这10筐苹果总共重多少千克?
=8+(-4)
解:根据题意得:
2+(-4)+2.5+3+(-0.5)+1.5+3+(-1)+0+(-2.5)
=(2+3+3)+(-4)+[2.5+(-2.5)]+[(-0.5)+(-1)+1.5]
=4
所以这10筐苹果总重量为:30×10+4=304(千克)
结合例1、例2的解答,思考:将怎样的加数结合在一起,可使运算简便?
把具有以下特征的数交换、结合相加:
(1)互为相反数的两个数;
(2)符号相同的数;
(3)相加能得到整数的数;
(4)分母相同的数;
(5)易于通分的数.
方法总结
1.计算:(-1.75)+(+7.3)+(-2.25)+(-8.5)+(+1.5)=[(-1.75)+(-2.25)]+[(+1.5)+(-8.5)]+(+7.3)运用了( )
A.加法的交换律
B.加法的结合律
C.加法的交换律和结合律
D.以上都不对
C
2.计算,可以运用( )
A.加法交换律
B.加法结合律
C.加法交换律和加法结合律
D.以上都不对
C
3.用运算律计算43+(- 78)+27+(-52)时,最为恰当的是( )
A.[43+(-78)]+[27+(-52)]
B. (43+27)+[(-78)+(-52)]
C.[43+(-52)]+[27+(-78)]
D.[27+(-78) ]+ [43-(-52)]
B
4.某日小明在一条南北方向的公路上跑步,他从A地出发,每隔10分钟记录下自己的跑步情况(向南为正方向,单位:米).
-1008,+1100,-976,+1010,-827,946
1小时后他停下来休息,此时他在A地的什么方向 距A地多远 小明共跑了多少米
解:(-1008)+1100+(-976)+1010+(-827)+946=245(米)
+++++=5867(米)
答:小明在A地的南边,距A地245米,小明共跑了5867米.
加法交换律:a+b=b+a
加法结合律:(a+b)+c=a+(b+c)
有理数的加法运算律
运算律的应用
使用方法:
(1)互为相反数的两个数;
(2)符号相同的数;
(3)相加能得到整数的数;
(4)分母相同的数;
(5)易于通分的数.
1.6 有理数的加法
1.6.1有理数的加法法则
1.了解有理数加法的意义,理解有理数加法法则的合理性
2.能运用有理数加法法则进行有理数的加法运算
填空
(1)一个有理数由_______和________两部分组成.
(2)若向东走20米记作20米,则向西走30米记作_________.
(3)若水位升高5米记作5米,则-5米表示________________
(4)小兰向西走了-8米,8米表示__________________________.
符号
绝对值
-30米
水位下降5米
小兰向东走了8米
小明在一条东西向的跑道上,先走了20 m,又走了30 m,能否确定他现在位于原来位置的哪个方向,与原来位置相距多少米?
小明最后的位置与行走方向有关,不妨规定向东为正,向西为负.
(1)若两次都是向东走
0
10
20
30
40
50
20
30
50
(+20)+(+30)=+50
东
西
小明位于原来位置的东边50 m处
小明在一条东西向的跑道上,先走了20 m,又走了30 m,能否确定他现在位于原来位置的哪个方向,与原来位置相距多少米?
(2)若两次都是向西走
-10
0
-20
-30
-40
-50
20
30
50
(-20)+(-30)=-50
东
西
小明位于原来位置的西边50 m处
小明在一条东西向的跑道上,先走了20 m,又走了30 m,能否确定他现在位于原来位置的哪个方向,与原来位置相距多少米?
(3)若第一次向东走20 m,第二次向西走30 m
东
-10
10
30
20
-20
0
20
30
10
(+20)+(-30)=-10
西
小明位于原来位置的西边10 m处
小明在一条东西向的跑道上,先走了20 m,又走了30 m,能否确定他现在位于原来位置的哪个方向,与原来位置相距多少米?
(4)若第一次向西走20 m,第二次向东走30 m
东
-10
10
30
20
-20
0
20
30
10
(-20)+(+30)=+10
西
小明位于原来位置的东边10 m处
小明在一条东西向的跑道上,先走了20 m,又走了30 m,能否确定他现在位于原来位置的哪个方向,与原来位置相距多少米?
(3)(4)两种情形中两个加数的正负号不同(通常可称为异号),让我们再试几次(下列算式中各个加数的正负号和绝对值仍分别表示运动的方向和路程):
(+4) +(-3)=( ), (+3) + (-10)=( ),
(-5) +(+7)=( ), (-6) +2 =( ).
+1
-7
+2
-4
(3)若第一次向东走20 m,第二次向西走30 m:(+20)+(-30)=-10
(4)若第一次向西走20 m,第二次向东走30 m:(-20)+(+30)=+10
还有两种特殊情形:
(5)若第一次向西走了30 m,第二次向东走了30 m,写成
算式是(-30)+(+30)=( ).
(6)若第一次向西走了30 m,第二次没走,写成算式是
(-30)+0=( ).
0
-30
从(1)~(6)所写出的算式中,你能总结出一些规律吗?
1.同号两数相加,取与加数相同的正负号,并把绝对值相加;
2.绝对值不相等的异号两数相加,取绝对值较大的加数的正负号,
并用较大的绝对值减去较小的绝对值;
3.互为相反数的两个数相加得0;
4.一个数与0相加,仍得这个数.
有理数的加法法则:
归纳
绝对值不相等的异号两数相加
互为相反数的两数相加
同号两数相加
绝对值不相等的异号两数相加
例1 计算:
(1)(+2)+(-11); (2)(-12)+(+12);
(3)(-)+(-); (4)(-3.4)+4.3 .
解:(1)(+2)+ (-11)=-(11-2)=-9.
(2) (-12) +(+12)=0.
(3)(-)+(-)=-(+)=-1;
(4)(-3.4)+4.3=+(4.3-3.4)=0.9.
1.如果两个数的和为正数,那么下列描述中,一定错误的是( )
A. 两个数均为正数
B. 两个数一个是正数,另一个是零
C. 两数一正一负,正数比负数的绝对值大
D. 两数一正一负,正数比负数的绝对值小
D
2. 计算:
(1) (-0.6)+(-2.7); (2) 3.7+(-8.4);
(3) 0+(-5.8); (4) 2025+(-2025).
解:(1) (-0.6)+(-2.7)=-(0.6+2.7)=-3.3
(2) 3.7+(-8.4)=-(8.4-3.7)=-4.7
(3) 0+(-5.8)=-5.8
(4) 2025+(-2025)=0
3.用“﹥”或“﹤”符号填空
(1)如果a>0,b>0,那么a+b____0;
(2) 如果a<0,b<0,那么a+b____0;
(3) 如果a>0,b<0,|a|>|b|,那么a+b____0;
(4) 如果a>0,b<0,|a|<|b|,那么a+b____0;
>
<
>
<
1.6.2有理数加法的运算律
1.理解加法交换律、结合律,并能运用字母表示运算律的内容
2.灵活熟练地运用加法交换律、结合律简化运算,并能运用加法运算律解决实际问题.
小学里我们学过的加法运算定律有哪些?举例说明.
引进了负数以后,这些运算律是否还成立呢?
也就是说,上面两个等式中,将5、3.5和2. 5换成任
意的有理数,是否仍然成立呢?
(1)a+b=b+a
(2)(a+b)+c=a+(b+c)
加法交换律 、加法结合律
5 +3.5 = 3.5+5
(5+3.5)+ 2.5 = 5 +(3.5+2.5)
(1) 任意选择两个有理数(至少有一个是负数),分别填入下列□和〇内,并比较两个运算结果:
□+〇和〇+□;
(2) 任意选择三个有理数(至少有一个是负数),分别填入下列□、〇和 内,并比较两个运算结果:
(□+〇)+ 和□+(〇+ ).
你能发现什么?
如:(1)(-30)+20= (2)20 +(-30)=
(3)8+(-5)= (4)(-5)+8=
(5)[8+(-5)]+(-4)= (6) 8+[(-5)+(-4)]=
-10
-10
3
3
-1
-1
有理数的加法仍满足交换律和结合律.
加法交换律:两个数相加,交换加数的位置,和不变.
a+b=b+a.
加法结合律:三个数相加,先把前两个数相加,或者先把后两个数相加,和不变 .(a+b)+c=a+(b+c).
归纳
解:(1) (+26) + (-18) + 5 + (-16)
=(26 + 5) +[(-18) + (-16)]
= 31 + (-34)
=-(34 - 31)
符号相同
例1 计算:(1) (+26) + (-18) + 5 + (-16);
=-3.
(2) (-1.75) + 1.5 + (+7.3) + (-2.25) + (-8.5).
解:(-1.75) + 1.5 + (+7.3) + (-2.25) + (-8.5)
=[(-1.75) + (-2.25)] + [1.5 + (-8.5)] + 7.3
= (-4) + (-7) + 7.3
=(-4) + 0.3
结果是整数
= (-4) + [(-7) + 7.3]
=-3.7.
整数部分相同
例2 10筐苹果,以每筐30千克为基准,超过的千克数记作正数,不足的千克数记作负数,记录如下:
2, -4, 2.5, 3, -0.5, 1.5, 3, -1, 0, -2.5.
问这10筐苹果总共重多少千克?
=8+(-4)
解:根据题意得:
2+(-4)+2.5+3+(-0.5)+1.5+3+(-1)+0+(-2.5)
=(2+3+3)+(-4)+[2.5+(-2.5)]+[(-0.5)+(-1)+1.5]
=4
所以这10筐苹果总重量为:30×10+4=304(千克)
结合例1、例2的解答,思考:将怎样的加数结合在一起,可使运算简便?
把具有以下特征的数交换、结合相加:
(1)互为相反数的两个数;
(2)符号相同的数;
(3)相加能得到整数的数;
(4)分母相同的数;
(5)易于通分的数.
方法总结
1.计算:(-1.75)+(+7.3)+(-2.25)+(-8.5)+(+1.5)=[(-1.75)+(-2.25)]+[(+1.5)+(-8.5)]+(+7.3)运用了( )
A.加法的交换律
B.加法的结合律
C.加法的交换律和结合律
D.以上都不对
C
2.计算,可以运用( )
A.加法交换律
B.加法结合律
C.加法交换律和加法结合律
D.以上都不对
C
3.用运算律计算43+(- 78)+27+(-52)时,最为恰当的是( )
A.[43+(-78)]+[27+(-52)]
B. (43+27)+[(-78)+(-52)]
C.[43+(-52)]+[27+(-78)]
D.[27+(-78) ]+ [43-(-52)]
B
4.某日小明在一条南北方向的公路上跑步,他从A地出发,每隔10分钟记录下自己的跑步情况(向南为正方向,单位:米).
-1008,+1100,-976,+1010,-827,946
1小时后他停下来休息,此时他在A地的什么方向 距A地多远 小明共跑了多少米
解:(-1008)+1100+(-976)+1010+(-827)+946=245(米)
+++++=5867(米)
答:小明在A地的南边,距A地245米,小明共跑了5867米.
加法交换律:a+b=b+a
加法结合律:(a+b)+c=a+(b+c)
有理数的加法运算律
运算律的应用
使用方法:
(1)互为相反数的两个数;
(2)符号相同的数;
(3)相加能得到整数的数;
(4)分母相同的数;
(5)易于通分的数.
同课章节目录
