1.10 有理数的除法(共21张PPT) 2025-2026学年数学华东师大版(2024)七年级上册
文档属性
| 名称 | 1.10 有理数的除法(共21张PPT) 2025-2026学年数学华东师大版(2024)七年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-23 23:39:54 | ||
图片预览







文档简介
(共21张PPT)
思考:若对象是有理数,倒数的定义是否会发生变化?有理数的除法该怎样计算呢?
小学里我们学过的倒数是怎样定义的?除法的意义是什么?它与乘法有什么关系?
乘积是1的两个数互为倒数.
1.10 有理数的除法
1.理解倒数的意义,会求有理数的倒数
2.理解有理数的除法法则,会进行有理数的除法运算
3.知道有理数是可以表示成两个整数之商的数,会进行分数的化简
(1)因为( )×(-4)=8,
所以8÷(-4)= .
(2)8×(- )= .
1
4
怎样计算8÷(-4)呢
-2
-2
-2
通过刚才的计算,观察8÷(-4)与 8×(- )有什么关系
1
4
8÷(-4)=8×(- )
1
4
除法可以转化为乘法来进行运算
试一试
与 互为倒数.
例如,
-2与 互为倒数,
小学里我们学过倒数的定义,对有理数仍有:
乘积是1的两个数互为倒数.
归纳
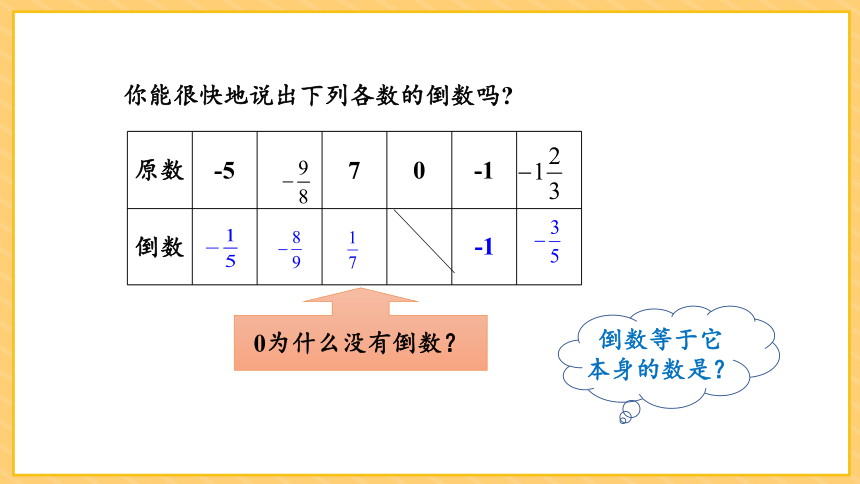
你能很快地说出下列各数的倒数吗
原数 -5 7 0 -1
倒数
-1
0为什么没有倒数?
倒数等于它本身的数是?
求一个数的倒数的方法:
①求一个不为0的整数的倒数,是用这个数作分母,1作分子的分数.
②求一个真分数或假分数的倒数,是把分子和分母交换位置后形成的分数.
③求一个带分数的倒数,要先把带分数化成假分数,再交换分子和分母的位置.
④求一个小数的倒数,要先把小数化成分数,再交换分子和分母的位置.
归纳
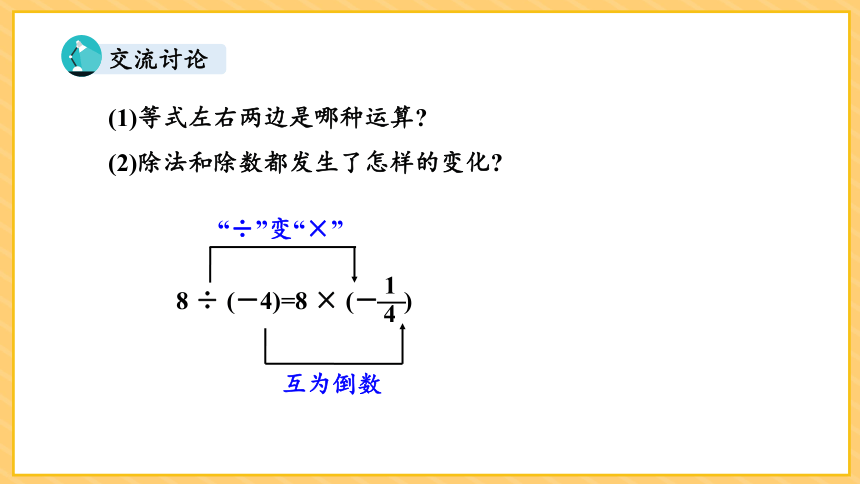
(1)等式左右两边是哪种运算
(2)除法和除数都发生了怎样的变化
互为倒数
8 ÷ (-4)=8 × (- )
1
4
“÷”变“×”
交流讨论
注意:0不能作除数.
有理数的除法法则:
1.除以一个数等于乘以这个数的倒数.
归纳
例1 计算:
(1)(-18)÷6;(2)(-)÷(-);(3)÷(-)
解:(1)(-18)÷6=(-18)×=-3
(2)(-)÷(-)=(-)×(-)=
(3)÷(-)=×(-)=-
你能发现商的正负号与除数和被除数正负号有什么关系吗?商的绝对值与除数及被除数的绝对值有什么关系呢?
两数相除,同号得___,异号得___, 并把绝对值相___.
0除以任何一个不等于0的数,都得__.
正
负
除
0
思考
两数相除,同号得___,异号得___, 并把绝对值相___.
0除以任何一个不等于0的数,都得__.
正
负
除
0
有理数的除法法则2:
归纳
两数相除,同号得___,异号得___, 并把绝对值相___.
0除以任何一个不等于0的数,都得__.
正
负
除
0
有理数的除法法则2:
归纳
有理数的本质:表示成两个整数之商的数
两数相除,同号得___,异号得___, 并把绝对值相___.
0除以任何一个不等于0的数,都得__.
正
负
除
0
有理数的除法法则2:
归纳
有理数的本质:表示成两个整数之商的数
①任何整数都是它除以1所得的商
②任何正分数(带分数先化成假分数)都是它的分子除以分母所得的商
③任何负分数可看成两个整数(其中一个是负整数)的商
-3==是-22与7或22与-7的商
例2 化简下列分数:
(1); (2).
解:(1)=(- 12) ÷3=-(12÷3)=-4.
(2)=(-24) ÷(-16)=24÷16=1
分数可以理解为两个整数的商,解答也可以书写成:
(1)=-=-4.
(2)==1
先定正负号
再算绝对值
例3 计算:
(1)(-)÷(-);(2)-(-)
解:(1)(-)÷(-)=÷=×=
(2)-(-)=×=
1.下列各组数中,互为倒数的是( )
A.2与-|-2|
B.-(+2)与
C.-(-2)与-
D.-与+(-2)
D
2. 下列计算中错误的是( )
A. (-5)÷ =(-5)×(-2)
B. ÷(-3)=3×(-3)
C.(-2)÷(-3)=(-2)×
D.
B
3. 两个互为相反数的有理数相除,商为( )
A.正数
B.负数
C.不存在
D.负数或不存在
D
4.(-56)÷(-2)÷(-8)
解:(-56)÷(-2)÷(-8)=-
有理数除法法则
两数相除,同号得正,异号得负,并把绝对值相除;0除以任何一个不等于0的数,都得0
化为有理数乘法,利用有理数乘法的运算律简化运算
思考:若对象是有理数,倒数的定义是否会发生变化?有理数的除法该怎样计算呢?
小学里我们学过的倒数是怎样定义的?除法的意义是什么?它与乘法有什么关系?
乘积是1的两个数互为倒数.
1.10 有理数的除法
1.理解倒数的意义,会求有理数的倒数
2.理解有理数的除法法则,会进行有理数的除法运算
3.知道有理数是可以表示成两个整数之商的数,会进行分数的化简
(1)因为( )×(-4)=8,
所以8÷(-4)= .
(2)8×(- )= .
1
4
怎样计算8÷(-4)呢
-2
-2
-2
通过刚才的计算,观察8÷(-4)与 8×(- )有什么关系
1
4
8÷(-4)=8×(- )
1
4
除法可以转化为乘法来进行运算
试一试
与 互为倒数.
例如,
-2与 互为倒数,
小学里我们学过倒数的定义,对有理数仍有:
乘积是1的两个数互为倒数.
归纳
你能很快地说出下列各数的倒数吗
原数 -5 7 0 -1
倒数
-1
0为什么没有倒数?
倒数等于它本身的数是?
求一个数的倒数的方法:
①求一个不为0的整数的倒数,是用这个数作分母,1作分子的分数.
②求一个真分数或假分数的倒数,是把分子和分母交换位置后形成的分数.
③求一个带分数的倒数,要先把带分数化成假分数,再交换分子和分母的位置.
④求一个小数的倒数,要先把小数化成分数,再交换分子和分母的位置.
归纳
(1)等式左右两边是哪种运算
(2)除法和除数都发生了怎样的变化
互为倒数
8 ÷ (-4)=8 × (- )
1
4
“÷”变“×”
交流讨论
注意:0不能作除数.
有理数的除法法则:
1.除以一个数等于乘以这个数的倒数.
归纳
例1 计算:
(1)(-18)÷6;(2)(-)÷(-);(3)÷(-)
解:(1)(-18)÷6=(-18)×=-3
(2)(-)÷(-)=(-)×(-)=
(3)÷(-)=×(-)=-
你能发现商的正负号与除数和被除数正负号有什么关系吗?商的绝对值与除数及被除数的绝对值有什么关系呢?
两数相除,同号得___,异号得___, 并把绝对值相___.
0除以任何一个不等于0的数,都得__.
正
负
除
0
思考
两数相除,同号得___,异号得___, 并把绝对值相___.
0除以任何一个不等于0的数,都得__.
正
负
除
0
有理数的除法法则2:
归纳
两数相除,同号得___,异号得___, 并把绝对值相___.
0除以任何一个不等于0的数,都得__.
正
负
除
0
有理数的除法法则2:
归纳
有理数的本质:表示成两个整数之商的数
两数相除,同号得___,异号得___, 并把绝对值相___.
0除以任何一个不等于0的数,都得__.
正
负
除
0
有理数的除法法则2:
归纳
有理数的本质:表示成两个整数之商的数
①任何整数都是它除以1所得的商
②任何正分数(带分数先化成假分数)都是它的分子除以分母所得的商
③任何负分数可看成两个整数(其中一个是负整数)的商
-3==是-22与7或22与-7的商
例2 化简下列分数:
(1); (2).
解:(1)=(- 12) ÷3=-(12÷3)=-4.
(2)=(-24) ÷(-16)=24÷16=1
分数可以理解为两个整数的商,解答也可以书写成:
(1)=-=-4.
(2)==1
先定正负号
再算绝对值
例3 计算:
(1)(-)÷(-);(2)-(-)
解:(1)(-)÷(-)=÷=×=
(2)-(-)=×=
1.下列各组数中,互为倒数的是( )
A.2与-|-2|
B.-(+2)与
C.-(-2)与-
D.-与+(-2)
D
2. 下列计算中错误的是( )
A. (-5)÷ =(-5)×(-2)
B. ÷(-3)=3×(-3)
C.(-2)÷(-3)=(-2)×
D.
B
3. 两个互为相反数的有理数相除,商为( )
A.正数
B.负数
C.不存在
D.负数或不存在
D
4.(-56)÷(-2)÷(-8)
解:(-56)÷(-2)÷(-8)=-
有理数除法法则
两数相除,同号得正,异号得负,并把绝对值相除;0除以任何一个不等于0的数,都得0
化为有理数乘法,利用有理数乘法的运算律简化运算
同课章节目录
