1.11 有理数的乘方(共31张PPT) 2025-2026学年数学华东师大版(2024)七年级上册
文档属性
| 名称 | 1.11 有理数的乘方(共31张PPT) 2025-2026学年数学华东师大版(2024)七年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-23 23:41:10 | ||
图片预览










文档简介
(共31张PPT)
1.11 有理数的乘方
1.11 第1课时 有理数的乘方
1.理解乘方的意义,能进行有理数的乘方运算
2.经历探索有量数乘方意义的过程,培养转化的思想方法.
你能利用学过的图形来解释平方、立方的意义吗?
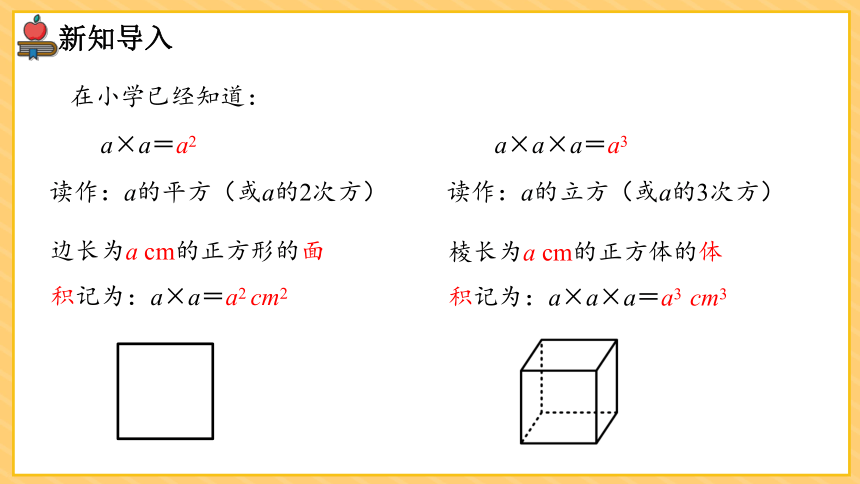
a×a=a2
在小学已经知道:
a×a×a=a3
读作:a的平方(或a的2次方)
读作:a的立方(或a的3次方)
a×a=a2
在小学已经知道:
a×a×a=a3
读作:a的平方(或a的2次方)
读作:a的立方(或a的3次方)
边长为a cm的正方形的面积记为:a×a=a2 cm2
棱长为a cm的正方体的体积记为:a×a×a=a3 cm3
2×2×2×2×2记作_____,读作___________.
(-2)×(-2)×(-2)×(-2)记作_____,读作___________.
-2的四次方
2的五次方
25
(-2)4
试一试
n个a相乘
一般的,n个相同的因数a相乘,即
记作
如:(-2)×(-2)×(-2)×(-2)= (-2)4
2×2×2×2=
n个a相乘
一般的,n个相同的因数a相乘,即
记作
如:(-2)×(-2)×(-2)×(-2)= (-2)4
2×2×2×2=
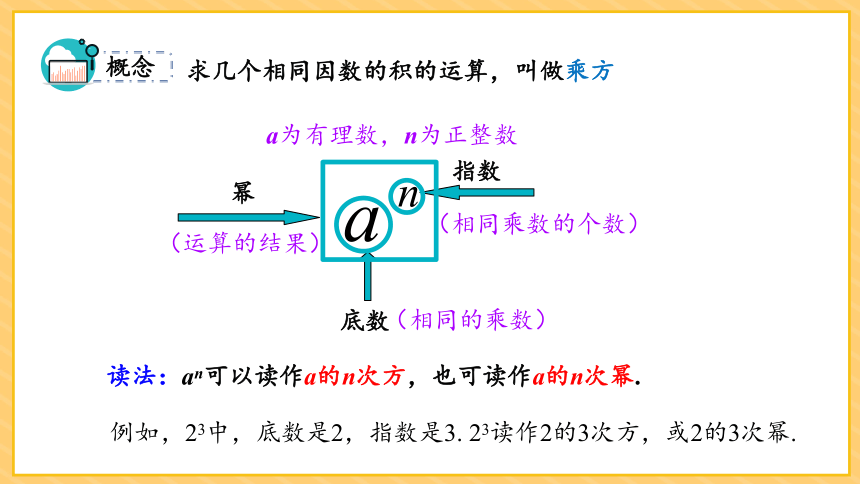
求几个相同因数的积的运算,叫做乘方
概念
概念
指数
底数
幂
读法:an可以读作a的n次方,也可读作a的n次幂.
(相同的乘数)
(相同乘数的个数)
(运算的结果)
a为有理数,n为正整数
例如,23中,底数是2,指数是3. 23读作2的3次方,或2的3次幂.
求几个相同因数的积的运算,叫做乘方
(1)45 表示____个_____相乘,指数是____,底数是____;
(2)(-2)10的底数是___,指数是 ____,表示 ;
(3)x m 表示____个____相乘,指数是____,底数是____;
(4)10的底数是____,指数是 ____;
-2
m
x
m
1
10
10
x
5
4
5
4
10个(-2)相乘
注意:一个数可看作这个数本身的1次方,a1就是a,指数1通常省略不写.
练一练
解:(1)(-2)3=(-2)×(-2)×(-2)=-8;
(2)(-2)4=(-2)×(-2)×(-2)×(-2)=16;
(3)(-2)5=(-2)×(-2)×(-2)×(-2)×(-2)=-32.
例1 计算:(1)(-2)3
;(2)(-2)4
;(3)(-2)5
你发现正负数次幂有什么规律吗?
正数的任何次幂都是正数
负数的奇次幂是负数,负数的偶次幂是正数
0的任何正整数次幂都是0
归纳
二者所表示的意义不一样.
因为 (-2)4表示的是2的相反数的4次幂,即-2的4次幂,结果是16;
而 -24表示的是2的4次幂的相反数,结果是-16.
所以二者的意义不一样.
(-2)4和-24所表示的意义一样吗?为什么?
思考
1. (-1)2等于( )
A.-1 B.1
C.-2 D.2
B
2.计算
A. B.
C. D.
D
3.下列对于-34的叙述正确的是( )
A.读作-3的4次幂
B.底数是-3,指数是4
C.表示4个3相乘的积的相反数
D.表示4个-3的积
C
4.计算:
(1) (-4)3; (2) (-2)4; (3)
解:(1) (-4)3=(-4)×(-4)×(-4)=-64;
(2) (-2)4=(-2)×(-2)×(-2)×(-2)=16;
有理数的乘方
乘方的定义
乘方的计算
这种求n个相同因数的积的运算叫做乘方,乘方的结果叫做幂.
2.正数的任何正整数次幂都是正数,0的任何正整数次幂都是0.
1.负数的奇次幂是负数,负数的偶次幂是正数.(偶为正、奇为负)
1.11 第2课时 科学记数法
在敦煌石窟所刻的算经中发现以下文字“一、十、百、千、万、十万、百万、千万、万万曰亿、一亿、十亿、百亿、千亿、万亿、百万亿、千万亿、万万亿曰兆……万万兆曰京……”
这段文字说明我国在古代表示大数的一种方法。
2023年末,中国人口约为14 0967 0000人;
月球的质量约为7350 0000 0000亿吨;
光的速度约为3 0000 0000米/秒;
地球离太阳约有1 5000 0000千米.
在生活中我们就会遇到一些比较大的数.例如:
你能快速读出这些数吗?
1.了解科学记数法的意义
2.会用科学记数法表示大数
3.能将用科学记数法表示的数还原成原数.
计算观察,10的乘方有什么特点?
思考:(1)指数与运算结果中0的个数有什么关系?
(2)指数与运算结果的数位有什么关系?
101=___, 102=____,103=_________,104=_______,
106=_________,1010=_____________,…
10
100
1000
10000
1000000
10000000000
,n恰好是1后面0的个数
n个0
反之,1后面有多少个0,10的幂指数就是多少.
,n比运算结果的位数少1
(n+1)位
7个0
(1)
(2)
(1)把下面各数写成10的幂的形式,即写成10( )
1000= 10000000= 100000000000= .
103
107
1011
做一做
300=3×
32000=3.2×
345000000=3.45×
=3×10( )
100
10000
100000000
2
4
8
=3.2×10( )
=3.45×10( )
读作“3.45乘10的8次方(幂)”
104,109,1015分别是几位数
这样,一个大于10的数就记成a×10n的形式,其中1≤a<10, n是正整数.这种记数法叫做科学记数法.
概念
例1 用科学记数法表示下列各数:
(1)678000; (2)1000000; (3)-14800.
解:(1)678000=6.78×105;
(2)1500000=1.5×106;
(3)-14800=-1.48×104.
用科学计数法表示一个n位整数时,10的指数是_____.
n-1
思考
归纳
用科学计数法表示一个n位整数时,10的指数是______
例2 下列用科学记数法写出的数,原来分别是什么数?
(1)4×103 (2)8.5×106 (3)3.96×104
(1)4000
(2)8500000
(3)39600
要将a×10n还原成整数就是把小数点向右移动n位,即a×10n原数的整数位数等于n+1,如果a中的位数不够,用“0”补足,注意符号.
方法总结
-3.251×107原数有__位整数
8
1.-268 000用科学记数法表示为( )
A.-268×103 B.-268×104
C.-26.8×104 D.-2.68×105
D
2.一个整数815550…0 用科学记数法表示为8.1555×,则原数中“0”的个数为( )
A.4 B.6 C.7 D.10
B
3.下列用科学记数法表示的数,原来各是什么数?
(1)2×107;(2)7.5×106;(3)8.04×103;(4)-2.96×105.
解:(1)20000000;(2)7500000;(3)8040;(4)-296000.
一个绝对值大于10的数都可记成a×10n的形式,其中a的取值范围1≤a<10 .n等于原数整数位减1.这种记数方法叫做科学记数法.
科学记数法
概念
应用
表示绝对值大于10的数
根据科学记数法写原数
n等于整数位数减1
原数整数位数等于指数n加1
1.11 有理数的乘方
1.11 第1课时 有理数的乘方
1.理解乘方的意义,能进行有理数的乘方运算
2.经历探索有量数乘方意义的过程,培养转化的思想方法.
你能利用学过的图形来解释平方、立方的意义吗?
a×a=a2
在小学已经知道:
a×a×a=a3
读作:a的平方(或a的2次方)
读作:a的立方(或a的3次方)
a×a=a2
在小学已经知道:
a×a×a=a3
读作:a的平方(或a的2次方)
读作:a的立方(或a的3次方)
边长为a cm的正方形的面积记为:a×a=a2 cm2
棱长为a cm的正方体的体积记为:a×a×a=a3 cm3
2×2×2×2×2记作_____,读作___________.
(-2)×(-2)×(-2)×(-2)记作_____,读作___________.
-2的四次方
2的五次方
25
(-2)4
试一试
n个a相乘
一般的,n个相同的因数a相乘,即
记作
如:(-2)×(-2)×(-2)×(-2)= (-2)4
2×2×2×2=
n个a相乘
一般的,n个相同的因数a相乘,即
记作
如:(-2)×(-2)×(-2)×(-2)= (-2)4
2×2×2×2=
求几个相同因数的积的运算,叫做乘方
概念
概念
指数
底数
幂
读法:an可以读作a的n次方,也可读作a的n次幂.
(相同的乘数)
(相同乘数的个数)
(运算的结果)
a为有理数,n为正整数
例如,23中,底数是2,指数是3. 23读作2的3次方,或2的3次幂.
求几个相同因数的积的运算,叫做乘方
(1)45 表示____个_____相乘,指数是____,底数是____;
(2)(-2)10的底数是___,指数是 ____,表示 ;
(3)x m 表示____个____相乘,指数是____,底数是____;
(4)10的底数是____,指数是 ____;
-2
m
x
m
1
10
10
x
5
4
5
4
10个(-2)相乘
注意:一个数可看作这个数本身的1次方,a1就是a,指数1通常省略不写.
练一练
解:(1)(-2)3=(-2)×(-2)×(-2)=-8;
(2)(-2)4=(-2)×(-2)×(-2)×(-2)=16;
(3)(-2)5=(-2)×(-2)×(-2)×(-2)×(-2)=-32.
例1 计算:(1)(-2)3
;(2)(-2)4
;(3)(-2)5
你发现正负数次幂有什么规律吗?
正数的任何次幂都是正数
负数的奇次幂是负数,负数的偶次幂是正数
0的任何正整数次幂都是0
归纳
二者所表示的意义不一样.
因为 (-2)4表示的是2的相反数的4次幂,即-2的4次幂,结果是16;
而 -24表示的是2的4次幂的相反数,结果是-16.
所以二者的意义不一样.
(-2)4和-24所表示的意义一样吗?为什么?
思考
1. (-1)2等于( )
A.-1 B.1
C.-2 D.2
B
2.计算
A. B.
C. D.
D
3.下列对于-34的叙述正确的是( )
A.读作-3的4次幂
B.底数是-3,指数是4
C.表示4个3相乘的积的相反数
D.表示4个-3的积
C
4.计算:
(1) (-4)3; (2) (-2)4; (3)
解:(1) (-4)3=(-4)×(-4)×(-4)=-64;
(2) (-2)4=(-2)×(-2)×(-2)×(-2)=16;
有理数的乘方
乘方的定义
乘方的计算
这种求n个相同因数的积的运算叫做乘方,乘方的结果叫做幂.
2.正数的任何正整数次幂都是正数,0的任何正整数次幂都是0.
1.负数的奇次幂是负数,负数的偶次幂是正数.(偶为正、奇为负)
1.11 第2课时 科学记数法
在敦煌石窟所刻的算经中发现以下文字“一、十、百、千、万、十万、百万、千万、万万曰亿、一亿、十亿、百亿、千亿、万亿、百万亿、千万亿、万万亿曰兆……万万兆曰京……”
这段文字说明我国在古代表示大数的一种方法。
2023年末,中国人口约为14 0967 0000人;
月球的质量约为7350 0000 0000亿吨;
光的速度约为3 0000 0000米/秒;
地球离太阳约有1 5000 0000千米.
在生活中我们就会遇到一些比较大的数.例如:
你能快速读出这些数吗?
1.了解科学记数法的意义
2.会用科学记数法表示大数
3.能将用科学记数法表示的数还原成原数.
计算观察,10的乘方有什么特点?
思考:(1)指数与运算结果中0的个数有什么关系?
(2)指数与运算结果的数位有什么关系?
101=___, 102=____,103=_________,104=_______,
106=_________,1010=_____________,…
10
100
1000
10000
1000000
10000000000
,n恰好是1后面0的个数
n个0
反之,1后面有多少个0,10的幂指数就是多少.
,n比运算结果的位数少1
(n+1)位
7个0
(1)
(2)
(1)把下面各数写成10的幂的形式,即写成10( )
1000= 10000000= 100000000000= .
103
107
1011
做一做
300=3×
32000=3.2×
345000000=3.45×
=3×10( )
100
10000
100000000
2
4
8
=3.2×10( )
=3.45×10( )
读作“3.45乘10的8次方(幂)”
104,109,1015分别是几位数
这样,一个大于10的数就记成a×10n的形式,其中1≤a<10, n是正整数.这种记数法叫做科学记数法.
概念
例1 用科学记数法表示下列各数:
(1)678000; (2)1000000; (3)-14800.
解:(1)678000=6.78×105;
(2)1500000=1.5×106;
(3)-14800=-1.48×104.
用科学计数法表示一个n位整数时,10的指数是_____.
n-1
思考
归纳
用科学计数法表示一个n位整数时,10的指数是______
例2 下列用科学记数法写出的数,原来分别是什么数?
(1)4×103 (2)8.5×106 (3)3.96×104
(1)4000
(2)8500000
(3)39600
要将a×10n还原成整数就是把小数点向右移动n位,即a×10n原数的整数位数等于n+1,如果a中的位数不够,用“0”补足,注意符号.
方法总结
-3.251×107原数有__位整数
8
1.-268 000用科学记数法表示为( )
A.-268×103 B.-268×104
C.-26.8×104 D.-2.68×105
D
2.一个整数815550…0 用科学记数法表示为8.1555×,则原数中“0”的个数为( )
A.4 B.6 C.7 D.10
B
3.下列用科学记数法表示的数,原来各是什么数?
(1)2×107;(2)7.5×106;(3)8.04×103;(4)-2.96×105.
解:(1)20000000;(2)7500000;(3)8040;(4)-296000.
一个绝对值大于10的数都可记成a×10n的形式,其中a的取值范围1≤a<10 .n等于原数整数位减1.这种记数方法叫做科学记数法.
科学记数法
概念
应用
表示绝对值大于10的数
根据科学记数法写原数
n等于整数位数减1
原数整数位数等于指数n加1
同课章节目录
