2.4.3 去括号和添括号(共25张PPT)2025-2026学年数学华东师大版(2024)七年级上册
文档属性
| 名称 | 2.4.3 去括号和添括号(共25张PPT)2025-2026学年数学华东师大版(2024)七年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-23 23:49:32 | ||
图片预览








文档简介
2.4.3 去括号和添括号
第1课时 去括号
在具体情境中体会去括号的必要性,了解去括号法则的依据
2. 掌握去括号法则,能利用其其进行简单的计算
1.树上起初有a只鸟,不一会儿飞来b只,后来又飞来c只,则树上共有______只鸟,我们还可以理解为,一共飞来_______只鸟,因而树上共有________只鸟。
①a+(b+c)=a+b+c
a+b+c
(b+c)
a+(b+c)
2.树上起初有a只鸟,不一会儿飞走b只,后来又走c只,则树上共有______只鸟,我们还可以理解为,一共飞走_______只鸟,因而树上共有________只鸟
②a-(b+c)=a-b-c
a-b-c
(b+c)
a-(b+c)
从这两个问题结果,你能发现什么关系?
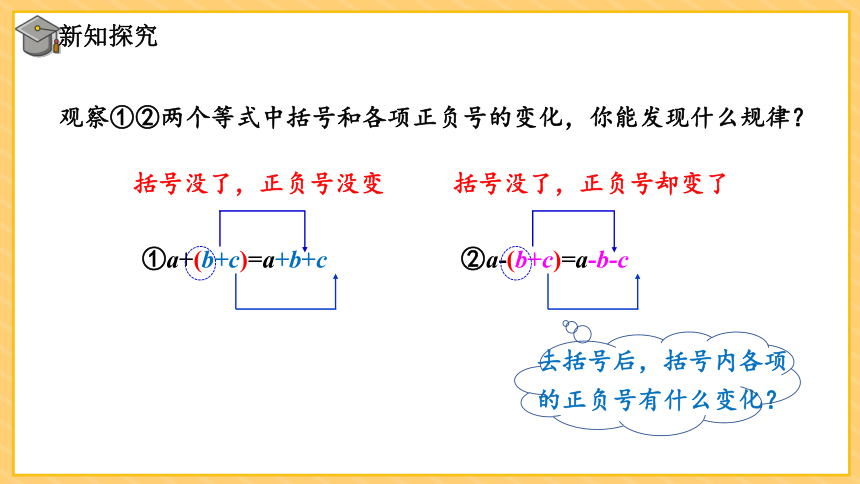
观察①②两个等式中括号和各项正负号的变化,你能发现什么规律?
②a-(b+c)=a-b-c
①a+(b+c)=a+b+c
括号没了,正负号没变
括号没了,正负号却变了
去括号后,括号内各项的正负号有什么变化?
(1)括号前面是“+”号,把括号和它前面的“+”号去掉,括号里各项都不变正负号;
(2)括号前面是“-”号,把括号和它前面的“-”号去掉,括号里各项都改变正负号.
归纳
例1 去括号:
(1)a+(b-c); (2)a-(b-c);
(3)a+(-b+c); (4)a- (-b-c).
解:(1)a+(b-c)=a +b-c.
(2)a-(b-c)=a-b+c.
(3)a+(-b+c)=a-b+c.
(4)a-(-b-c)=a+b+c.
注意:
①准确理解去括号的规律,去括号时括号内的每一项的符号都要考虑,做到要变都变,要不变,则都不变
②括号内原有几项去掉括号后仍有几项
例2 化简下列各式:
(1)8a+2b+(5a-b);
(2)(5a-3b)-3(a2-2b).
(1)解: 原式=8a+2b+5a-b
=13a+b
(2)解:原式= (5a-3b)-(3a2-6b)
= 5a-3b-3a2+6b
= -3a2+5a+3b
注意:
当括号前面有数字因数时,可应用乘法分配律将这个数字因数先乘以括号内的每一项,再去括号,切勿漏乘.
例3 先去括号,再合并同类项:
(1)(x+y-z)+(x-y+z)-(x-y-z);
(2)(a2+2ab+b2)-(a2-2ab+b2);
(3)3(2x2-y2)-2(3y2-2x2).
解:(1)(x+y-z)+(x-y+z) -(x-y-z)=x+y+z+x-y+z-x+y+z
(2)(a2+2ab+b2) -(a2-2ab+b2)=a2+2ab+b2-a2+2ab-b2
(3)3(2x2-y2)-2(3y2-2x2)=6x2-3y2-6y2+4x2
=x+y+z
=4ab
=10x2-9y2
1.将-(2 x2-3 x )去括号得( B )
A. -2 x2-3 x B. -2 x2+3 x
C. 2 x2-3 x D. 2 x2+3 x
B
2.若a-b表示一个数,则它的相反数是( )
A. -a+b . B.-a-b.
C. a+b D.a-b
A
3.化简:
(1)(6x2-x+3)-(-4x2+6x-2);
(2)(2x-3y)-3(4x-2y).
解:(1)原式=6x2-x+3+4x2-6x+2=10x2-7x+5.
(2)原式=2x-3y-12x+6y=-10x+3y.
2.4.3 去括号和添括号 第2课时 添括号
1.能用自己的语言总结添括号法则,并能运用法则进行多项式的化简求值
(1)a+(b+c)=a+b+c (2)a-(b+c)=a-b-c
括号没了,正负号没变
括号没了,正负号却变了
去括号
如果把上面的(1)(2)两个等式中等号的两边对调,观察对调后两个等式中括号和各项正负号的变化,你能得出什么结论?
(1)a+b+c=a+(b+c) . (2)a-b-c=a-(b+c) .
正负号均不变
正负号均改变
发现
1.所添括号前面是“+”号,括到括号里的各项都不改变正负号;
2.所添括号前面是“-”号,括到括号里的各项都改变正负号.
归纳
在括号内填入适当的项:
(1)x2-x+1=x2-( )
(2) 2x2-3x-1=2x2+( )
(3) (a-b)-(c-d)=a-( )
x-1
-3x-1
解:(3)(a-b)-(c-d)=a-b-c+d=a-(b+c-d)
b+c-d
做一做
例1 计算:
(1)214a+47a+53a;
(2)214a-39a-61a.
解:(1)214a+47a+53a
=214a+(47a+53a)
=214a+100a
=314a;
(2)214a-39a-61a
=214a-(39a+61a)
=214a-100a
=114a.
适当添加括号,可使计算简便.
添括号与去括号的过程正好相反,添括号是否正确,可以用去括号检验!
1.下面添括号错误的是( ? )
A.-x+5=-(x+5)?????????
B.-7m-2n=-(7m+2n)
C.a2-3=+( a2-3)??????????
D.2x-y=-(y-2x)
A
2.不改变代数式a2+2a-b+c的值,下列添括号错误的是( ?????)
A.a2+(2a-b+c) ???????????
B.a2-(-2a+b-c)
C.a2-(2a+b+c) ???????????
D.a2+2a+(c-b)
C
3.若x-2y的值是3,则1+2x-4y的值是( ?????)
A.7 ??????????????
B.-5 ????????????
C.5 ??????????????
D. -4
A
4.把多项式a2-2bc+b2-c2写成两个代数式差的形式使被减式中只含字母a,减式中不含字母a.
a2-(2bc-b2+c2)
5.计算109a+428a-156a+141a-128a-44a.
解:原式=109a+428a+141a-156a-128a-44a
=(109a+141a)+(428a-128a)-(156a+44a)
=250a+300a-200a
=550a-200a
=350a.
添括号
所添括号前面是“+”号,括到括号内的各项都不改变符号
所添括号前面是“-”号,括到括号内的各项都改变符号
去括号
检
验
添括号
所添括号前面是“+”号,括到括号内的各项都不改变符号
所添括号前面是“-”号,括到括号内的各项都改变符号
添括号与去括号都只改变式子的形状,不改变式子的值,属于多项式的恒等变形,即“形变而值不变”
化简求值
第1课时 去括号
在具体情境中体会去括号的必要性,了解去括号法则的依据
2. 掌握去括号法则,能利用其其进行简单的计算
1.树上起初有a只鸟,不一会儿飞来b只,后来又飞来c只,则树上共有______只鸟,我们还可以理解为,一共飞来_______只鸟,因而树上共有________只鸟。
①a+(b+c)=a+b+c
a+b+c
(b+c)
a+(b+c)
2.树上起初有a只鸟,不一会儿飞走b只,后来又走c只,则树上共有______只鸟,我们还可以理解为,一共飞走_______只鸟,因而树上共有________只鸟
②a-(b+c)=a-b-c
a-b-c
(b+c)
a-(b+c)
从这两个问题结果,你能发现什么关系?
观察①②两个等式中括号和各项正负号的变化,你能发现什么规律?
②a-(b+c)=a-b-c
①a+(b+c)=a+b+c
括号没了,正负号没变
括号没了,正负号却变了
去括号后,括号内各项的正负号有什么变化?
(1)括号前面是“+”号,把括号和它前面的“+”号去掉,括号里各项都不变正负号;
(2)括号前面是“-”号,把括号和它前面的“-”号去掉,括号里各项都改变正负号.
归纳
例1 去括号:
(1)a+(b-c); (2)a-(b-c);
(3)a+(-b+c); (4)a- (-b-c).
解:(1)a+(b-c)=a +b-c.
(2)a-(b-c)=a-b+c.
(3)a+(-b+c)=a-b+c.
(4)a-(-b-c)=a+b+c.
注意:
①准确理解去括号的规律,去括号时括号内的每一项的符号都要考虑,做到要变都变,要不变,则都不变
②括号内原有几项去掉括号后仍有几项
例2 化简下列各式:
(1)8a+2b+(5a-b);
(2)(5a-3b)-3(a2-2b).
(1)解: 原式=8a+2b+5a-b
=13a+b
(2)解:原式= (5a-3b)-(3a2-6b)
= 5a-3b-3a2+6b
= -3a2+5a+3b
注意:
当括号前面有数字因数时,可应用乘法分配律将这个数字因数先乘以括号内的每一项,再去括号,切勿漏乘.
例3 先去括号,再合并同类项:
(1)(x+y-z)+(x-y+z)-(x-y-z);
(2)(a2+2ab+b2)-(a2-2ab+b2);
(3)3(2x2-y2)-2(3y2-2x2).
解:(1)(x+y-z)+(x-y+z) -(x-y-z)=x+y+z+x-y+z-x+y+z
(2)(a2+2ab+b2) -(a2-2ab+b2)=a2+2ab+b2-a2+2ab-b2
(3)3(2x2-y2)-2(3y2-2x2)=6x2-3y2-6y2+4x2
=x+y+z
=4ab
=10x2-9y2
1.将-(2 x2-3 x )去括号得( B )
A. -2 x2-3 x B. -2 x2+3 x
C. 2 x2-3 x D. 2 x2+3 x
B
2.若a-b表示一个数,则它的相反数是( )
A. -a+b . B.-a-b.
C. a+b D.a-b
A
3.化简:
(1)(6x2-x+3)-(-4x2+6x-2);
(2)(2x-3y)-3(4x-2y).
解:(1)原式=6x2-x+3+4x2-6x+2=10x2-7x+5.
(2)原式=2x-3y-12x+6y=-10x+3y.
2.4.3 去括号和添括号 第2课时 添括号
1.能用自己的语言总结添括号法则,并能运用法则进行多项式的化简求值
(1)a+(b+c)=a+b+c (2)a-(b+c)=a-b-c
括号没了,正负号没变
括号没了,正负号却变了
去括号
如果把上面的(1)(2)两个等式中等号的两边对调,观察对调后两个等式中括号和各项正负号的变化,你能得出什么结论?
(1)a+b+c=a+(b+c) . (2)a-b-c=a-(b+c) .
正负号均不变
正负号均改变
发现
1.所添括号前面是“+”号,括到括号里的各项都不改变正负号;
2.所添括号前面是“-”号,括到括号里的各项都改变正负号.
归纳
在括号内填入适当的项:
(1)x2-x+1=x2-( )
(2) 2x2-3x-1=2x2+( )
(3) (a-b)-(c-d)=a-( )
x-1
-3x-1
解:(3)(a-b)-(c-d)=a-b-c+d=a-(b+c-d)
b+c-d
做一做
例1 计算:
(1)214a+47a+53a;
(2)214a-39a-61a.
解:(1)214a+47a+53a
=214a+(47a+53a)
=214a+100a
=314a;
(2)214a-39a-61a
=214a-(39a+61a)
=214a-100a
=114a.
适当添加括号,可使计算简便.
添括号与去括号的过程正好相反,添括号是否正确,可以用去括号检验!
1.下面添括号错误的是( ? )
A.-x+5=-(x+5)?????????
B.-7m-2n=-(7m+2n)
C.a2-3=+( a2-3)??????????
D.2x-y=-(y-2x)
A
2.不改变代数式a2+2a-b+c的值,下列添括号错误的是( ?????)
A.a2+(2a-b+c) ???????????
B.a2-(-2a+b-c)
C.a2-(2a+b+c) ???????????
D.a2+2a+(c-b)
C
3.若x-2y的值是3,则1+2x-4y的值是( ?????)
A.7 ??????????????
B.-5 ????????????
C.5 ??????????????
D. -4
A
4.把多项式a2-2bc+b2-c2写成两个代数式差的形式使被减式中只含字母a,减式中不含字母a.
a2-(2bc-b2+c2)
5.计算109a+428a-156a+141a-128a-44a.
解:原式=109a+428a+141a-156a-128a-44a
=(109a+141a)+(428a-128a)-(156a+44a)
=250a+300a-200a
=550a-200a
=350a.
添括号
所添括号前面是“+”号,括到括号内的各项都不改变符号
所添括号前面是“-”号,括到括号内的各项都改变符号
去括号
检
验
添括号
所添括号前面是“+”号,括到括号内的各项都不改变符号
所添括号前面是“-”号,括到括号内的各项都改变符号
添括号与去括号都只改变式子的形状,不改变式子的值,属于多项式的恒等变形,即“形变而值不变”
化简求值
同课章节目录
