2.3 整式(共43张PPT)2025-2026学年数学华东师大版(2024)七年级上册
文档属性
| 名称 | 2.3 整式(共43张PPT)2025-2026学年数学华东师大版(2024)七年级上册 |
|
|
| 格式 | pptx | ||
| 文件大小 | 38.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-23 00:00:00 | ||
图片预览








文档简介
(共43张PPT)
2.3 整式
2.3.1 单项式
1.理解单项式的概念,会判断一个代数式是不是单项式
2.理解单项式的系数和次数的概念,会求一个单项式的
次数、系数
同学们,美食节来啦!我们要化身美食小当家,制作美味的蛋挞、蛋糕和果汁饮料.在制作过程中藏着一些数学问题,快来迎接挑战吧!
1.一份蛋挞需要 5 个鸡蛋,每个鸡蛋价格是 y 元,那制作x份蛋挞需要____个鸡蛋,鸡蛋成本是____元
2.要做一个长为 a 分米,高度是 h 分米的正方形蛋糕,蛋糕的底面面积为_____平方分米 ,蛋糕体积为_____立方分米
3.调制苹果梨汁,梨汁量是苹果汁的 2.5 倍 ,用 m 升苹果汁 ,需要____升梨汁,再加入 n 升纯净水 ,每升 3 元,纯净水成本是____元
5x
5xy
3n
2.5m
a
a h
列出的这些代数式在组成形式上有什么共同点?
5x
5xy
3n
2.5m
a
a h
列出的这些代数式在组成形式上有什么共同点?
代数式都是由数与字母的乘积组成
5x
5xy
3n
2.5m
a
a h
概念
像这样,由数与字母的乘积组成的代数式叫做单项式
单独一个数或一个字母也是单项式.
单项式中不含加减运算,分母 中不能出现字母
例1 判断下列哪些是单项式?
不是
是
不是
不是
是
代数式有加法运算
代数式是1和x的商
代数式是x和y的商
(1)x+2;(2)-7;(3);(5)-;(6)
1.单独一个数或一个字母是单项式.
2.不含加减运算,单项式只含有乘积运算.
3.单项式数字因数与字母可能一个或多个.
4.可以含有除以数的运算,不能含有除以字母的运算.
判断单项式的方法
方法总结
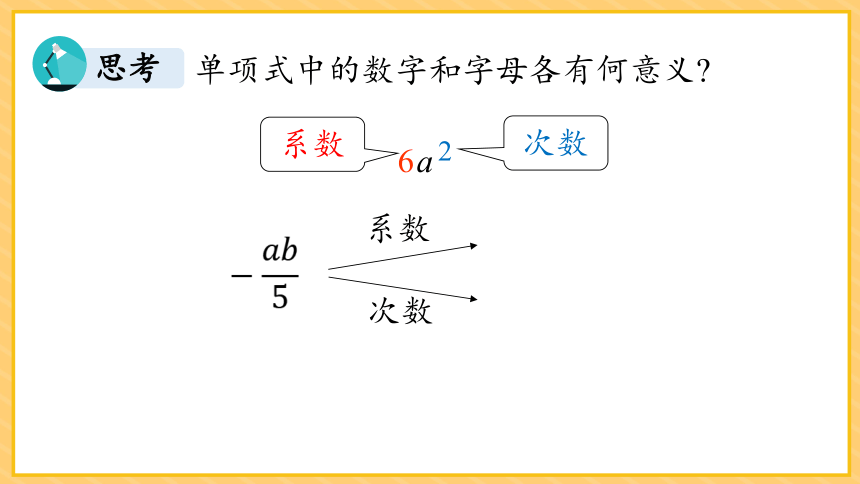
单项式中的数字和字母各有何意义
思考
a
2
6
次数
系数
次数
系数
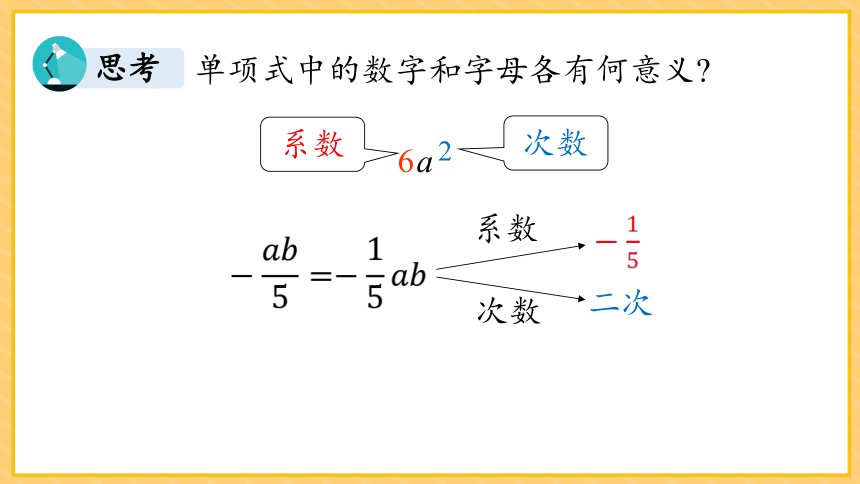
单项式中的数字和字母各有何意义
思考
a
2
6
次数
二次
系数
次数
系数
a
2
6
次数
二次
系数
次数
系数
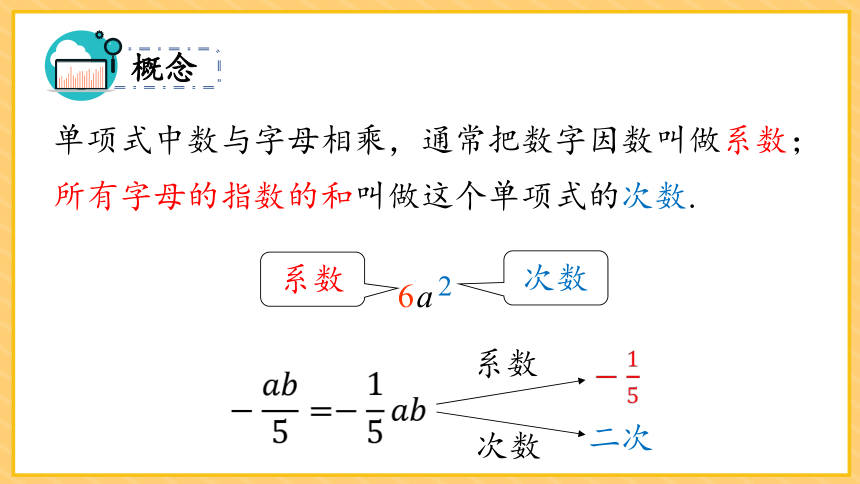
单项式中数与字母相乘,通常把数字因数叫做系数;所有字母的指数的和叫做这个单项式的次数.
概念
例2 判断下列各代数式是不是单项式,如果不是,请说明理由;如果是,请指出它们的系数和次数.
(1)x+1; (2)-
解:(1)x+1不是单项式,因为代数式中出现了加法运算
(2)- 是单项式,它的系数是-
(1)单项式的系数包括它前面的符号,如-2ab的系数是-2,而非2
(2)单项式的系数是1 或-1 时,通常“1”省略不写,如-a,-xy的系
数是-1,ab的系数是1,而不能说没有系数.
(3)单独一个非零数的次数是0,如-1,25等,它们的次数都是0;
(4)若单项式中的某个字母没有写指数,则这个字母的指数是 1.
注意事项
例3 若 是关于 x,y 的一个四次单项式,m,n应满足的条件?
单项式次数是2+n
所以m≠ 2,n=2.
2+n=4,
m-2 ≠ 0,
解:m,n要满足
1.在下列代数式:,-4,-abc,0,x-y,中,单项式有( )
A.3个 B.4个 C.5个 D.6个
B
2.关于单项式-23x2y2z,下列结论正确的是 ( )
A.系数是-2,次数是4
B.系数是-2,次数是5
C.系数是-2,次数是8
D.系数是-23,次数是5
D
3. 已知一个单项式的系数是2,次数是3,则这个单项式可以是( )
A.-2xy2 B.3x2
C.2xy3 D.2x3
D
4.已知单项式6x2y与2a2bm+2的次数相同,求m2-2的值.
解:根据题意,得m+2+2=2+1,
所以m=-1.
所以m2-2m=(-1)2-2×(-1)=3.
单项式
由数与字母的积组成的代数式
所有字母的指数的和
单项式中的数字因数
概念
系数
次数
2.3.2 多项式
1.理解多项式、整式的概念;
2.会确定一个多项式的项数和次数.
列代数式:
(1)若三角形的三条边长分别为a、b、c,则这个三角形的周长是________;
(2)某班有男生x人,女生21人,这个班的学生一共________人;
(3)图中阴影部分的面积为___________.
a+b+c
(x+21)
2ar-πr2
列出的这些代数式有什
么共同特点 它们与单
项式有什么区别?
上面列出的代数式都是由几个单项式相加而成的.
上面列出的代数式都是由几个单项式相加而成的.
a+b+c
2ar-πr2
(x+21)
1.几个单项式的和叫做多项式.
概念
2.在多项式中,每个单项式叫做多项式的项.
3.不含字母的项叫做常数项.
4.多项式中次数最高项的次数就是这个多项式的次数.
5.一个多项式含有几项,就叫做几项式.
多项式及其有关概念:
a+b+c
2ar-πr2
(x+21)
项
常数项
多项式的次数
单项式与多项式统称为整式
多项式5x3-7x-6有______项,分别是_____________,其中-6是_______,这个多项式的次数是_____,该多项式是___次___项式
三
5x2 、-7x、-6
常数项
3
确定多项式的次数时:
①先找出每一项(即每一个单项式)的次数;
②取次数最高项的次数.
找多项式的项,必须连同前面的正负号
三
三
注意
解: (1)多项式 a3-a2b+ab2-b3的项有 a3、-a2b、
ab2、-b3 ,次数是 3.
(2)多项式3n4-2n2+1 的项有3n4 、-2n2 、1,
次数是4.
例1 指出下列多项式的项和次数:
(1)a3-a2b+ab2-b3;(2)3n4-2n2+1.
例2 指出下列多项式是几次几项式:
(1) x3-x+1; (2) x3-2x2y2+3y2.
解:(1) x3-x+1是三次三项式.
(2) x3-2x2y2+3y2是四次三项式.
1.下列代数式中,整式为( )
A. x +1
B.
C.
D.
A
2.已知一个多项式是三次二项式,则这个多项式可以是( )
A.x2-2x+1
B.2x3+1
C.x2-2x
D.x3-2x2+1
B
3.下列说法中正确的是( )
A. 多项式 x2+2x+18是三次三项式
B. 多项式3x2+2y2-5的项是3x2,2y2,5
C. xy2-1是单项式
D. 3m3-2m-5+m2的一次项是-2m,二次项的系数是1
D
次数:所有字母的指数的和.
系数:单项式中的数因数.
次数:多项式中次数最高项的次数.
整式
项:多项式中的每个单项式叫做多项式的项.
其中不含字母的项叫做常数项
单项式
多项式
2.3.3 升幂排列和降幂排列
1.会把一个多项式按某一字母作降幂排列或升幂排列,初步体验排列组合的思想与数学的美感.
运用加法交换律,可以任意交换多项式各项的位置.将多项式x2+x+1中各项的位置交换,可以得到哪些不同的排列方式?
x2+x+1 1+x+x2
x+x2+1 x+1+x2
1+x2+x x2+1+x
试一试
你认为哪几种比较整齐?
字母x的指数从大到小或从小到大的排列方式比较整齐
把一个多项式的各项按某一字母的指数从大到小的顺序排列,叫做把这个多项式按这个字母的降幂排列.
把一个多项式的各项按某一字母的指数从小到大的顺序排列,叫做把这个多项式按这个字母的升幂排列.
x2+x+1 1+x+x2
x+x2+1 x+1+x2
1+x2+x x2+1+x
把一个多项式的各项按某一字母的指数从大到小的顺序排列,叫做把这个多项式按这个字母的降幂排列.
归纳
例如:多项式x2+x+1的降幂、升幂排列:
把一个多项式的各项按某一字母的指数从小到大的顺序排列,叫做把这个多项式按这个字母的升幂排列.
多项式5x2+3x-2x3-1按x的降幂、升幂排列结果是什么
思路:先找出每一项x的指数,再按照x的指数从大到小进行排列.
思路:先找出每一项x的指数,再按照x的指数从大到小进行排列.
按x的降幂排列:-2x3+5x2+3x-1.
按x的升幂排列:-1+3x+5x2-2x3.
多项式5x2+3x-2x3-1按x的降幂、升幂排列结果是什么
①把一个多项式的各项按某个字母的升幂排列时,常数项要作为第一项;而降幂排列时,要把常数项写在最后;
②一个多项式中含有两个(或两个以上)字母时,必须清楚是按哪一个字母的升幂(或降幂)排列.
如a4b3-2a3b4-a2b2+4ab5+3是按a的降幂排列,
方法总结
例1 把多项式2r-1+ r3- r2按r的升幂排列.
解:按r的升幂排列为:
解: (1)按a的升幂排列为: b2 -3ab3-3a2b + a3 .
(2)按a的降幂排列为: a3 -3a2b -3ab3 +b2 .
例2 把多项式a3 +b2 -3a2b-3ab3重新排列:
(1)按a的升幂排列;(2)按a的降幂排列.
试试将这个多项式按b的升幂(或降幂)排列.
注意:
(1)重新排列多项式时,每一项一定要连同它的正负号一起移动;
(2)含有两个或两个以上字母的多项式,通常按其中某一字母的升幂或降幂排列.
1.多项式a3-a2-1+a按a的升幂排列是( )
A.a3-a2-a+1
B.-1+a-a2+a3
C.a3-a2+a-1
D.-1+a3-a2+a
B
2.多项式5x2y+y3-3xy2-x3按x的降幂排列是( )
A. 5x2y-3xy2+y3-x3
B. y3-3xy2+5x2y-x3
C. 5x2y-x3-3xy2+y3
D. -x3+5x2y-3xy2+y3
D
3.将多项式2x2-3x3-5+2x按照字母x的降幂排列后,第三项是( )
A.2x2 B.-3x3
C.-5 D.2x
4.多项式3xy2-2x2y+x3y4-3是 次 项式,把它按字母x的降幂排列为 .
D
七
x3y4-2x2y+3xy2-3
四
2.3 整式
2.3.1 单项式
1.理解单项式的概念,会判断一个代数式是不是单项式
2.理解单项式的系数和次数的概念,会求一个单项式的
次数、系数
同学们,美食节来啦!我们要化身美食小当家,制作美味的蛋挞、蛋糕和果汁饮料.在制作过程中藏着一些数学问题,快来迎接挑战吧!
1.一份蛋挞需要 5 个鸡蛋,每个鸡蛋价格是 y 元,那制作x份蛋挞需要____个鸡蛋,鸡蛋成本是____元
2.要做一个长为 a 分米,高度是 h 分米的正方形蛋糕,蛋糕的底面面积为_____平方分米 ,蛋糕体积为_____立方分米
3.调制苹果梨汁,梨汁量是苹果汁的 2.5 倍 ,用 m 升苹果汁 ,需要____升梨汁,再加入 n 升纯净水 ,每升 3 元,纯净水成本是____元
5x
5xy
3n
2.5m
a
a h
列出的这些代数式在组成形式上有什么共同点?
5x
5xy
3n
2.5m
a
a h
列出的这些代数式在组成形式上有什么共同点?
代数式都是由数与字母的乘积组成
5x
5xy
3n
2.5m
a
a h
概念
像这样,由数与字母的乘积组成的代数式叫做单项式
单独一个数或一个字母也是单项式.
单项式中不含加减运算,分母 中不能出现字母
例1 判断下列哪些是单项式?
不是
是
不是
不是
是
代数式有加法运算
代数式是1和x的商
代数式是x和y的商
(1)x+2;(2)-7;(3);(5)-;(6)
1.单独一个数或一个字母是单项式.
2.不含加减运算,单项式只含有乘积运算.
3.单项式数字因数与字母可能一个或多个.
4.可以含有除以数的运算,不能含有除以字母的运算.
判断单项式的方法
方法总结
单项式中的数字和字母各有何意义
思考
a
2
6
次数
系数
次数
系数
单项式中的数字和字母各有何意义
思考
a
2
6
次数
二次
系数
次数
系数
a
2
6
次数
二次
系数
次数
系数
单项式中数与字母相乘,通常把数字因数叫做系数;所有字母的指数的和叫做这个单项式的次数.
概念
例2 判断下列各代数式是不是单项式,如果不是,请说明理由;如果是,请指出它们的系数和次数.
(1)x+1; (2)-
解:(1)x+1不是单项式,因为代数式中出现了加法运算
(2)- 是单项式,它的系数是-
(1)单项式的系数包括它前面的符号,如-2ab的系数是-2,而非2
(2)单项式的系数是1 或-1 时,通常“1”省略不写,如-a,-xy的系
数是-1,ab的系数是1,而不能说没有系数.
(3)单独一个非零数的次数是0,如-1,25等,它们的次数都是0;
(4)若单项式中的某个字母没有写指数,则这个字母的指数是 1.
注意事项
例3 若 是关于 x,y 的一个四次单项式,m,n应满足的条件?
单项式次数是2+n
所以m≠ 2,n=2.
2+n=4,
m-2 ≠ 0,
解:m,n要满足
1.在下列代数式:,-4,-abc,0,x-y,中,单项式有( )
A.3个 B.4个 C.5个 D.6个
B
2.关于单项式-23x2y2z,下列结论正确的是 ( )
A.系数是-2,次数是4
B.系数是-2,次数是5
C.系数是-2,次数是8
D.系数是-23,次数是5
D
3. 已知一个单项式的系数是2,次数是3,则这个单项式可以是( )
A.-2xy2 B.3x2
C.2xy3 D.2x3
D
4.已知单项式6x2y与2a2bm+2的次数相同,求m2-2的值.
解:根据题意,得m+2+2=2+1,
所以m=-1.
所以m2-2m=(-1)2-2×(-1)=3.
单项式
由数与字母的积组成的代数式
所有字母的指数的和
单项式中的数字因数
概念
系数
次数
2.3.2 多项式
1.理解多项式、整式的概念;
2.会确定一个多项式的项数和次数.
列代数式:
(1)若三角形的三条边长分别为a、b、c,则这个三角形的周长是________;
(2)某班有男生x人,女生21人,这个班的学生一共________人;
(3)图中阴影部分的面积为___________.
a+b+c
(x+21)
2ar-πr2
列出的这些代数式有什
么共同特点 它们与单
项式有什么区别?
上面列出的代数式都是由几个单项式相加而成的.
上面列出的代数式都是由几个单项式相加而成的.
a+b+c
2ar-πr2
(x+21)
1.几个单项式的和叫做多项式.
概念
2.在多项式中,每个单项式叫做多项式的项.
3.不含字母的项叫做常数项.
4.多项式中次数最高项的次数就是这个多项式的次数.
5.一个多项式含有几项,就叫做几项式.
多项式及其有关概念:
a+b+c
2ar-πr2
(x+21)
项
常数项
多项式的次数
单项式与多项式统称为整式
多项式5x3-7x-6有______项,分别是_____________,其中-6是_______,这个多项式的次数是_____,该多项式是___次___项式
三
5x2 、-7x、-6
常数项
3
确定多项式的次数时:
①先找出每一项(即每一个单项式)的次数;
②取次数最高项的次数.
找多项式的项,必须连同前面的正负号
三
三
注意
解: (1)多项式 a3-a2b+ab2-b3的项有 a3、-a2b、
ab2、-b3 ,次数是 3.
(2)多项式3n4-2n2+1 的项有3n4 、-2n2 、1,
次数是4.
例1 指出下列多项式的项和次数:
(1)a3-a2b+ab2-b3;(2)3n4-2n2+1.
例2 指出下列多项式是几次几项式:
(1) x3-x+1; (2) x3-2x2y2+3y2.
解:(1) x3-x+1是三次三项式.
(2) x3-2x2y2+3y2是四次三项式.
1.下列代数式中,整式为( )
A. x +1
B.
C.
D.
A
2.已知一个多项式是三次二项式,则这个多项式可以是( )
A.x2-2x+1
B.2x3+1
C.x2-2x
D.x3-2x2+1
B
3.下列说法中正确的是( )
A. 多项式 x2+2x+18是三次三项式
B. 多项式3x2+2y2-5的项是3x2,2y2,5
C. xy2-1是单项式
D. 3m3-2m-5+m2的一次项是-2m,二次项的系数是1
D
次数:所有字母的指数的和.
系数:单项式中的数因数.
次数:多项式中次数最高项的次数.
整式
项:多项式中的每个单项式叫做多项式的项.
其中不含字母的项叫做常数项
单项式
多项式
2.3.3 升幂排列和降幂排列
1.会把一个多项式按某一字母作降幂排列或升幂排列,初步体验排列组合的思想与数学的美感.
运用加法交换律,可以任意交换多项式各项的位置.将多项式x2+x+1中各项的位置交换,可以得到哪些不同的排列方式?
x2+x+1 1+x+x2
x+x2+1 x+1+x2
1+x2+x x2+1+x
试一试
你认为哪几种比较整齐?
字母x的指数从大到小或从小到大的排列方式比较整齐
把一个多项式的各项按某一字母的指数从大到小的顺序排列,叫做把这个多项式按这个字母的降幂排列.
把一个多项式的各项按某一字母的指数从小到大的顺序排列,叫做把这个多项式按这个字母的升幂排列.
x2+x+1 1+x+x2
x+x2+1 x+1+x2
1+x2+x x2+1+x
把一个多项式的各项按某一字母的指数从大到小的顺序排列,叫做把这个多项式按这个字母的降幂排列.
归纳
例如:多项式x2+x+1的降幂、升幂排列:
把一个多项式的各项按某一字母的指数从小到大的顺序排列,叫做把这个多项式按这个字母的升幂排列.
多项式5x2+3x-2x3-1按x的降幂、升幂排列结果是什么
思路:先找出每一项x的指数,再按照x的指数从大到小进行排列.
思路:先找出每一项x的指数,再按照x的指数从大到小进行排列.
按x的降幂排列:-2x3+5x2+3x-1.
按x的升幂排列:-1+3x+5x2-2x3.
多项式5x2+3x-2x3-1按x的降幂、升幂排列结果是什么
①把一个多项式的各项按某个字母的升幂排列时,常数项要作为第一项;而降幂排列时,要把常数项写在最后;
②一个多项式中含有两个(或两个以上)字母时,必须清楚是按哪一个字母的升幂(或降幂)排列.
如a4b3-2a3b4-a2b2+4ab5+3是按a的降幂排列,
方法总结
例1 把多项式2r-1+ r3- r2按r的升幂排列.
解:按r的升幂排列为:
解: (1)按a的升幂排列为: b2 -3ab3-3a2b + a3 .
(2)按a的降幂排列为: a3 -3a2b -3ab3 +b2 .
例2 把多项式a3 +b2 -3a2b-3ab3重新排列:
(1)按a的升幂排列;(2)按a的降幂排列.
试试将这个多项式按b的升幂(或降幂)排列.
注意:
(1)重新排列多项式时,每一项一定要连同它的正负号一起移动;
(2)含有两个或两个以上字母的多项式,通常按其中某一字母的升幂或降幂排列.
1.多项式a3-a2-1+a按a的升幂排列是( )
A.a3-a2-a+1
B.-1+a-a2+a3
C.a3-a2+a-1
D.-1+a3-a2+a
B
2.多项式5x2y+y3-3xy2-x3按x的降幂排列是( )
A. 5x2y-3xy2+y3-x3
B. y3-3xy2+5x2y-x3
C. 5x2y-x3-3xy2+y3
D. -x3+5x2y-3xy2+y3
D
3.将多项式2x2-3x3-5+2x按照字母x的降幂排列后,第三项是( )
A.2x2 B.-3x3
C.-5 D.2x
4.多项式3xy2-2x2y+x3y4-3是 次 项式,把它按字母x的降幂排列为 .
D
七
x3y4-2x2y+3xy2-3
四
同课章节目录
