大单元复习三 几何的作图问题与简单计算(含答案)2025-2026学年数学人教版(2024)七年级上册
文档属性
| 名称 | 大单元复习三 几何的作图问题与简单计算(含答案)2025-2026学年数学人教版(2024)七年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 194.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-24 00:04:58 | ||
图片预览



文档简介
大单元复习三 几何的作图问题与简单计算
题型归类
题型一 作图问题
例1 作图题(尺规作图,保留痕迹,不写作法):
如图,平面内有四个点,,,.根据下列语句画图:
(1) 画直线;
(2) 画射线交直线于点;
(3) 连接,用圆规在线段的延长线上截取.
变式跟进
1.作图题:
(1) 如图①,,,三点不在同一直线上,请作线段、射线、直线;
(2) 如图②,已知线段,,请作一条线段,使其等于(尺规作图,请保留作图痕迹).
题型二 与线段相关的计算
例2 如图,线段,是线段的中点,是线段的中点.
(1) 如图①,求线段的长;
(2) 如图②,是线段上的一点,且满足,求的长;
(3) 在(2)的条件下,是线段上的一点,且,求的长.
变式跟进
2.如图,已知,是线段的中点,点把线段分成的两部分,求线段的长.
请补充完成下列解答:
解:是线段的中点,,
_ _ _ _ _ _ _ _ _ _ .
,
_ _ _ _ _ _ _ _ _ _ .
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ .
3.如图,是线段上的一点, ,,是线段的中点,是线段上一点.
(1) 若为线段的中点,求的长;
(2) 若为线段的一个三等分点,求的长.
题型三 角度转化及计算
例3 [2023深圳模拟]下列角的单位换算中,正确的是( )
A. B.
C. D.
变式跟进
4.计算:
(1) ;
(2) .
题型四 方向角
例4 [2023长沙模拟]轮船在灯塔的北偏东 的方向上,轮船在灯塔的东南方向,则的度数为_ _ _ _ _ _ .
变式跟进
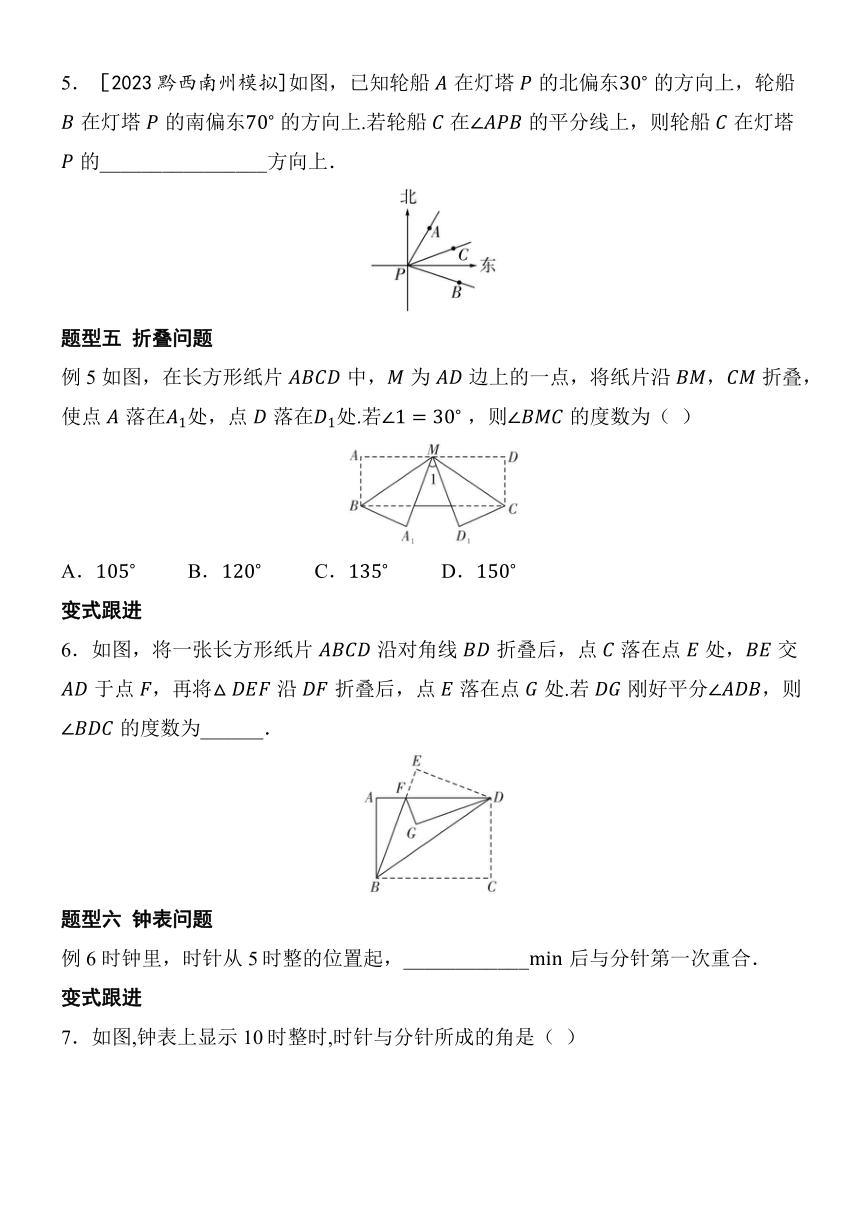
5.[2023黔西南州模拟]如图,已知轮船在灯塔的北偏东 的方向上,轮船在灯塔的南偏东 的方向上.若轮船在的平分线上,则轮船在灯塔的_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ 方向上.
题型五 折叠问题
例5 如图,在长方形纸片中,为边上的一点,将纸片沿,折叠,使点落在处,点落在处.若 ,则的度数为( )
A. B. C. D.
变式跟进
6.如图,将一张长方形纸片沿对角线折叠后,点落在点处,交于点,再将沿折叠后,点落在点处.若刚好平分,则的度数为_ _ _ _ _ _ .
题型六 钟表问题
例6 时钟里,时针从5时整的位置起,_ _ _ _ _ _ _ _ _ _ _ _ 后与分针第一次重合.
变式跟进
7.如图,钟表上显示10时整时,时针与分针所成的角是( )
A. B. C. D.
题型七 角的和差运算
例7 [[2023深圳模拟]]如图,点,,在同一条直线上,,分别平分和.
(1) 求的度数;
(2) 若 ,求的度数;
(3) 若,求的度数.
变式跟进
8.如图,将一副三角尺的顶点叠合在一起,记为点.
(1) 当 时,求的度数;
(2) 请探究和的度数之间满足的数量关系,并说明理由.
题型八 余角与补角
例8 [2024娄底模拟]如图,是直线上一点,与互为余角,是的平分线.
(1) 求的度数;
(2) 若 ,求的度数;
(3) 若,求的度数.
变式跟进
9.[2023宁乡模拟]如图,已知,的余角比小 .
(1) 求的度数;
(2) 过点作射线,使得,请你求出的度数.
过关训练
A组·基础达标
1.[2023邵阳模拟]下列关系正确的是( )
A. B.
C. D.
2.[2024北京模拟]如图,已知 , ,则的度数为( )
A. B. C. D.
3.[2023南阳模拟]如图,,为的中点,点在线段上,且,则的长度是( )
A. B. C. D.
4把一副三角尺与按如图所示拼在一起,其中,,三点在同一直线上,为的平分线,为的平分线,则的度数是_ _ _ _ _ _ .
5.[2023岳阳模拟]如图,是线段上一点,且,动点,从点同时出发,分别朝着点,运动,且点的运动速度是点的.当时,的长为_ _ _ _ .
6.如图,已知为线段上一点,,,,分别为线段,的中点,求线段与的长.
7.已知点在直线上,在直线的同侧作射线,.
(1) 如图①,若 ,,求的度数;
(2) 如图②,若平分,平分, ,求的度数.
B组·能力提升
8.[2024深圳模拟]如图,点在线段的延长线上,且线段,第一次操作:分别取线段和的中点,;第二次操作:分别取线段和的中点,;第三次操作:分别取线段和的中点,……连续这样操作20次,则每次的两个中点所形成的所有线段之和( )
A. B. C. D.
9.[2024长沙模拟]如图,已知线段,点在线段的延长线上,且,为线段的中点.
(1) 求线段的长;
(2) 点在线段上,且,请判断点是不是线段的中点,并说明理由.
10.[2024邵东模拟]线段的计算和角的计算有紧密联系,它们之间的解法可以互相迁移.下面是某节课的学习片段,请完成探索过程:
(1) 课上,老师提出问题:如图①,是线段上一点,,分别是线段,的中点,当时,求线段的长度.下面是小泽根据老师的要求进行的分析及解答过程,请你补全解答过程:
,分别是线段,的中点, _ _ _ _ _ _ _ _ _ _ _ _ . , _ _ _ _ ,
(2) 小泽举一反三,发现有些角度的计算也可以用相似的方法进行转化.如图②,已知 ,是角内部的一条射线,,分别是,的平分线.求的度数.请同学们尝试解决该问题.
同组的同学很善于思考,她提出新的问题:如果(2)中其他条件不变,将射线绕点旋转到的外部,则的度数是_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ .
大单元复习三 几何的作图问题与简单计算
题型归类
题型一 作图问题
例1 (1) 解:如答图,直线即为所求作.
例1答图
(2) 如答图,射线和点即为所求作.
例1答图
(3) 如答图,线段,即为所求作.
例1答图
变式跟进
1.(1) 解:如答图①,线段、射线、直线即为所求作.
变式跟进1答图①
(2) 如答图②,线段即为所求作.
变式跟进1答图②
题型二 与线段相关的计算
例2 (1) 解:是线段的中点,是线段的中点,
,,
.
.
(2) ,
设,则.
,
,解得,
,,
.
(3) ①当点在点左边时,如答图①.
例2答图①
,,
.
②当点在点右边时,如答图②.
例2答图②
,,
.
综上所述,的长为4或8.
变式跟进
2.; 12; ; 8; ; 12; ; 20
3.(1) 解:是线段的中点,为线段的中点,
,.
,
.
(2) ,,
,,
是线段的中点,
,
为线段的一个三等分点,
或,
或.
的长为3或5.
题型三 角度转化及计算
例3 D
变式跟进
4.(1)
(2)
题型四 方向角
例4
变式跟进
5.北偏东
题型五 折叠问题
例5 A
变式跟进
6.
题型六 钟表问题
例6
变式跟进
7.B
题型七 角的和差运算
例7 (1) 解:,分别平分和,
,,
,
即 .
(2) ,
.
(3) ,
设 , .
,
,
解得,
,
,
.
变式跟进
8.(1) 解: , ,
.
,
.
(2) .理由如下:
,
.
,
.
即 .
题型八 余角与补角
例8 (1) 解:与互余,
,
.
(2) 与互余, ,
.
又是的平分线,
,
.
(3) 设 ,则 , .
,
,
解得,
.
变式跟进
9.(1) 解:设 ,则 ,
由题意,得,
解得,
.
(2) 由(1)得, .
.
①当射线在内部时,
.
②当射线在外部时,
.
综上所述,的度数为 或 .
过关训练
A组·基础达标
1.D 2.B 4.D
4.
5.12
6.解:,,
,
.
,分别为线段,的中点,
,,
.
7.(1) 解: ,
,
即 .
,
设 , ,
,
解得, .
(2) ,
.
平分,平分,
,,
,
.
B组·能力提升
8.C
9.(1) 解:,,
.
为线段的中点,
,
.
(2) 是线段的中点.理由如下:
,,.
,.
由(1)可知,
,
,
是线段的中点.
10.(1) ; ; 8
(2) 解:,分别是,的平分线,
,,
.
(3) 或
题型归类
题型一 作图问题
例1 作图题(尺规作图,保留痕迹,不写作法):
如图,平面内有四个点,,,.根据下列语句画图:
(1) 画直线;
(2) 画射线交直线于点;
(3) 连接,用圆规在线段的延长线上截取.
变式跟进
1.作图题:
(1) 如图①,,,三点不在同一直线上,请作线段、射线、直线;
(2) 如图②,已知线段,,请作一条线段,使其等于(尺规作图,请保留作图痕迹).
题型二 与线段相关的计算
例2 如图,线段,是线段的中点,是线段的中点.
(1) 如图①,求线段的长;
(2) 如图②,是线段上的一点,且满足,求的长;
(3) 在(2)的条件下,是线段上的一点,且,求的长.
变式跟进
2.如图,已知,是线段的中点,点把线段分成的两部分,求线段的长.
请补充完成下列解答:
解:是线段的中点,,
_ _ _ _ _ _ _ _ _ _ .
,
_ _ _ _ _ _ _ _ _ _ .
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ .
3.如图,是线段上的一点, ,,是线段的中点,是线段上一点.
(1) 若为线段的中点,求的长;
(2) 若为线段的一个三等分点,求的长.
题型三 角度转化及计算
例3 [2023深圳模拟]下列角的单位换算中,正确的是( )
A. B.
C. D.
变式跟进
4.计算:
(1) ;
(2) .
题型四 方向角
例4 [2023长沙模拟]轮船在灯塔的北偏东 的方向上,轮船在灯塔的东南方向,则的度数为_ _ _ _ _ _ .
变式跟进
5.[2023黔西南州模拟]如图,已知轮船在灯塔的北偏东 的方向上,轮船在灯塔的南偏东 的方向上.若轮船在的平分线上,则轮船在灯塔的_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ 方向上.
题型五 折叠问题
例5 如图,在长方形纸片中,为边上的一点,将纸片沿,折叠,使点落在处,点落在处.若 ,则的度数为( )
A. B. C. D.
变式跟进
6.如图,将一张长方形纸片沿对角线折叠后,点落在点处,交于点,再将沿折叠后,点落在点处.若刚好平分,则的度数为_ _ _ _ _ _ .
题型六 钟表问题
例6 时钟里,时针从5时整的位置起,_ _ _ _ _ _ _ _ _ _ _ _ 后与分针第一次重合.
变式跟进
7.如图,钟表上显示10时整时,时针与分针所成的角是( )
A. B. C. D.
题型七 角的和差运算
例7 [[2023深圳模拟]]如图,点,,在同一条直线上,,分别平分和.
(1) 求的度数;
(2) 若 ,求的度数;
(3) 若,求的度数.
变式跟进
8.如图,将一副三角尺的顶点叠合在一起,记为点.
(1) 当 时,求的度数;
(2) 请探究和的度数之间满足的数量关系,并说明理由.
题型八 余角与补角
例8 [2024娄底模拟]如图,是直线上一点,与互为余角,是的平分线.
(1) 求的度数;
(2) 若 ,求的度数;
(3) 若,求的度数.
变式跟进
9.[2023宁乡模拟]如图,已知,的余角比小 .
(1) 求的度数;
(2) 过点作射线,使得,请你求出的度数.
过关训练
A组·基础达标
1.[2023邵阳模拟]下列关系正确的是( )
A. B.
C. D.
2.[2024北京模拟]如图,已知 , ,则的度数为( )
A. B. C. D.
3.[2023南阳模拟]如图,,为的中点,点在线段上,且,则的长度是( )
A. B. C. D.
4把一副三角尺与按如图所示拼在一起,其中,,三点在同一直线上,为的平分线,为的平分线,则的度数是_ _ _ _ _ _ .
5.[2023岳阳模拟]如图,是线段上一点,且,动点,从点同时出发,分别朝着点,运动,且点的运动速度是点的.当时,的长为_ _ _ _ .
6.如图,已知为线段上一点,,,,分别为线段,的中点,求线段与的长.
7.已知点在直线上,在直线的同侧作射线,.
(1) 如图①,若 ,,求的度数;
(2) 如图②,若平分,平分, ,求的度数.
B组·能力提升
8.[2024深圳模拟]如图,点在线段的延长线上,且线段,第一次操作:分别取线段和的中点,;第二次操作:分别取线段和的中点,;第三次操作:分别取线段和的中点,……连续这样操作20次,则每次的两个中点所形成的所有线段之和( )
A. B. C. D.
9.[2024长沙模拟]如图,已知线段,点在线段的延长线上,且,为线段的中点.
(1) 求线段的长;
(2) 点在线段上,且,请判断点是不是线段的中点,并说明理由.
10.[2024邵东模拟]线段的计算和角的计算有紧密联系,它们之间的解法可以互相迁移.下面是某节课的学习片段,请完成探索过程:
(1) 课上,老师提出问题:如图①,是线段上一点,,分别是线段,的中点,当时,求线段的长度.下面是小泽根据老师的要求进行的分析及解答过程,请你补全解答过程:
,分别是线段,的中点, _ _ _ _ _ _ _ _ _ _ _ _ . , _ _ _ _ ,
(2) 小泽举一反三,发现有些角度的计算也可以用相似的方法进行转化.如图②,已知 ,是角内部的一条射线,,分别是,的平分线.求的度数.请同学们尝试解决该问题.
同组的同学很善于思考,她提出新的问题:如果(2)中其他条件不变,将射线绕点旋转到的外部,则的度数是_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ .
大单元复习三 几何的作图问题与简单计算
题型归类
题型一 作图问题
例1 (1) 解:如答图,直线即为所求作.
例1答图
(2) 如答图,射线和点即为所求作.
例1答图
(3) 如答图,线段,即为所求作.
例1答图
变式跟进
1.(1) 解:如答图①,线段、射线、直线即为所求作.
变式跟进1答图①
(2) 如答图②,线段即为所求作.
变式跟进1答图②
题型二 与线段相关的计算
例2 (1) 解:是线段的中点,是线段的中点,
,,
.
.
(2) ,
设,则.
,
,解得,
,,
.
(3) ①当点在点左边时,如答图①.
例2答图①
,,
.
②当点在点右边时,如答图②.
例2答图②
,,
.
综上所述,的长为4或8.
变式跟进
2.; 12; ; 8; ; 12; ; 20
3.(1) 解:是线段的中点,为线段的中点,
,.
,
.
(2) ,,
,,
是线段的中点,
,
为线段的一个三等分点,
或,
或.
的长为3或5.
题型三 角度转化及计算
例3 D
变式跟进
4.(1)
(2)
题型四 方向角
例4
变式跟进
5.北偏东
题型五 折叠问题
例5 A
变式跟进
6.
题型六 钟表问题
例6
变式跟进
7.B
题型七 角的和差运算
例7 (1) 解:,分别平分和,
,,
,
即 .
(2) ,
.
(3) ,
设 , .
,
,
解得,
,
,
.
变式跟进
8.(1) 解: , ,
.
,
.
(2) .理由如下:
,
.
,
.
即 .
题型八 余角与补角
例8 (1) 解:与互余,
,
.
(2) 与互余, ,
.
又是的平分线,
,
.
(3) 设 ,则 , .
,
,
解得,
.
变式跟进
9.(1) 解:设 ,则 ,
由题意,得,
解得,
.
(2) 由(1)得, .
.
①当射线在内部时,
.
②当射线在外部时,
.
综上所述,的度数为 或 .
过关训练
A组·基础达标
1.D 2.B 4.D
4.
5.12
6.解:,,
,
.
,分别为线段,的中点,
,,
.
7.(1) 解: ,
,
即 .
,
设 , ,
,
解得, .
(2) ,
.
平分,平分,
,,
,
.
B组·能力提升
8.C
9.(1) 解:,,
.
为线段的中点,
,
.
(2) 是线段的中点.理由如下:
,,.
,.
由(1)可知,
,
,
是线段的中点.
10.(1) ; ; 8
(2) 解:,分别是,的平分线,
,,
.
(3) 或
同课章节目录
