第六章 几何图形初步质量评估(含答案)2025-2026学年数学人教版(2024)七年级上册
文档属性
| 名称 | 第六章 几何图形初步质量评估(含答案)2025-2026学年数学人教版(2024)七年级上册 | 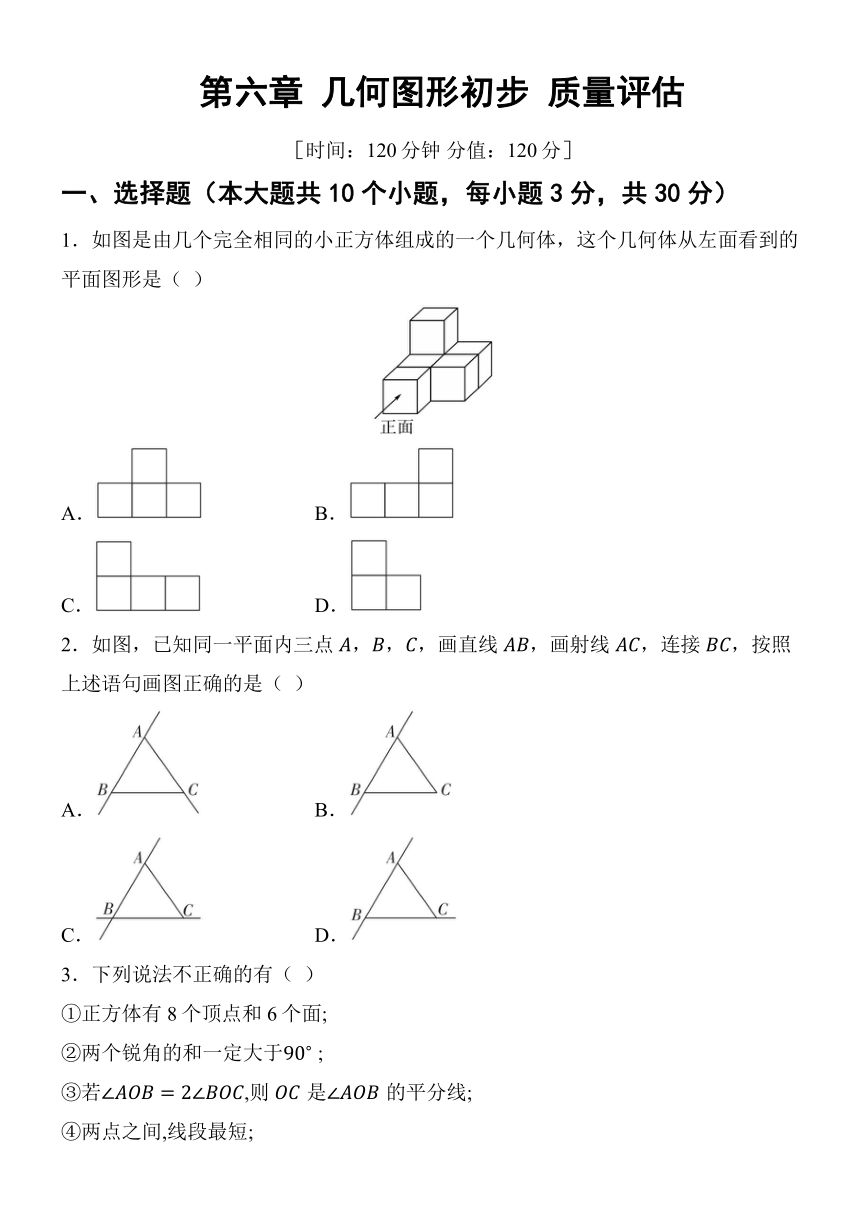 | |
| 格式 | docx | ||
| 文件大小 | 180.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-24 00:10:25 | ||
图片预览





文档简介
第六章 几何图形初步 质量评估
[时间:120分钟 分值:120分]
一、选择题(本大题共10个小题,每小题3分,共30分)
1.如图是由几个完全相同的小正方体组成的一个几何体,这个几何体从左面看到的平面图形是( )
A. B.
C. D.
2.如图,已知同一平面内三点,,,画直线,画射线,连接,按照上述语句画图正确的是( )
A. B.
C. D.
3.下列说法不正确的有( )
①正方体有8个顶点和6个面;
②两个锐角的和一定大于 ;
③若,则是的平分线;
④两点之间,线段最短;
⑤钝角的补角一定大于这个角本身;
⑥射线也可以表示为射线.
A.2个 B.3个 C.4个 D.5个
4.如图,已知线段,是的中点,点在线段上,,那么线段的长为( )
A. B. C. D.
5.已知 与 互为余角,,则 的补角是( )
A. B. C. D.
6.已知线段,延长至点,使,反向延长至点,使,那么线段的长是线段长的( )
A. B. C. D.
7.如图,是的平分线,, ,则的度数是( )
A. B. C. D.
8.当钟表上显示12时15分时,时针与分针的夹角为( )
A. B. C. D.
9.如图,已知数轴上,,三点表示的数分别为,0,4,动点从点出发,沿数轴向右运动.在运动过程中,始终为的中点,始终为的中点,点在从点运动到点的过程中,则线段的长度为( )
A.6 B.5 C.4 D.3
10.如图,为直线上一点,为直角,平分,平分,平分,有下列结论:与互为余角; ;与互为补角; .其中正确的是( )
A.①②③④ B.③④ C.②③ D.②③④
二、填空题(本大题共6个小题,每小题3分,共18分)
11.单位换算:_ _ _ _ .
12.如图,射线表示_ _ _ _ _ _ _ _ _ _ _ _ 方向,射线表示_ _ _ _ _ _ _ _ _ _ _ _ 方向.
13.将一张长方形纸片按如图所示的方式折叠,,为折痕,点落在点处,点落在点处,且与重合.若 ,则的度数为_ _ _ _.
14.如图,已知线段,延长至点,使得,若是的中点,,则的长为_ _ _ _ .
15.若一个角的余角比这个角的补角的一半小 ,则这个角的度数为_ _ _ _ _ _ .
16.定义:把有公共顶点和一条公共边的两个角称为“共边角”.
(1) 当两个“共边角”为 和 时,它们非公共边的两边的夹角的度数为_ _ _ _ _ _ _ _ _ _ ;
(2) 若两个“共边角”非公共边的两边所成的角是 ,则这两个角的平分线的夹角度数为_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ .
三、解答题(本大题共9个小题,共72分)
17.(6分)计算:
(1) ;
(2) ;
(3) .
18.(6分)如图,在同一平面内有,,三点.
(1) 画直线,线段和射线;
(2) 在线段上任取一点(不同于点,),连接线段;
(3) 在(1),(2)的条件下,图中有_ _ _ _ 条线段.
19.(6分)如图,已知 , ,平分,平分,求和的度数.
20.(8分)如图①,有一块长方形纸板,长是宽的2倍.现将其四角各剪去一个正方形,折成如图②所示的高为的无盖长方体盒子(纸板厚度忽略不计).
(1) 请在图①中的长方形纸板中画出无盖长方体盒子的平面示意图,用实线表示剪切线,虚线表示折痕;
(2) 如果无盖长方体盒子底面宽为,长是宽的3倍,原长方形纸板的长可以用两个不同的代数式表示,则这两个代数式分别为_ _ _ _ _ _ _ _ _ _ 或_ _ _ _ _ _ _ _ _ _ ;
(3) 如果原长方形纸板的宽为,经过剪切折成的无盖长方体盒子底面的周长为_ _ _ _ _ _ _ _ _ _ .
21.(8分)阅读感悟:
数学课上,老师给出了如下问题:如图①,一条直线上有,,,四点,线段,为线段的中点,线段,请你补全图形,并求的长度.
以下是小华的解答过程:
解:如图②,
因为线段,为线段 的中点,
所以 _ _ _ _ _ _ _ _ .
因为,
所以 _ _ _ _ .
小斌认为这个题应该有两种情况,小华只考虑了点 在线段 上,事实上,点 还可以在线段 的延长线上.
解决问题:
(1) 请填空:将小华的解答过程补充完整;
(2) 根据小斌的想法,请你在备用图中画出另一种情况对应的示意图,并求出此时的长度.
22.(9分)定义:如果线段上的一个点将这条线段分成长度分别是,的两部分,并且满足,那么这个点叫作这条线段的“三高四新点”.
(1) 如图,点是线段的“三高四新点”,,且,则_ _ _ _ ;
(2) 若点也是(1)中线段的“三高四新点”(不同于点),求与的数量关系.
23.(9分)如图,与互为补角,与互为余角.
(1) 若,求的度数.
(2) 若.
① 求的度数;
② 如果平分,求的度数.
24.(10分)如图①, ,将三角板的直角顶点放置在点处,平分.
(1) 若 ,则_ _ _ _ _ _ ,_ _ _ _ _ _ .
(2) 若 , ,试判断 , 之间的数量关系,并说明理由.
(3) 如图②,当三角板绕着点顺时针旋转一定角度,使得在的内部,在的外部.若 , , , 是否还存在(2)中的数量关系?若存在,请说明理由;若不存在,请求出 , 的数量关系.
25.(10分)【阅读理解】
已知,,为数轴上三点,若点到点的距离是点到点的距离的2倍,我们就称点是的“妙点”.例如,如图①,点表示的数为,点表示的数为2,点表示的数为1,点到点的距离是2,到点的距离是1,那么点是的“妙点”.又例如,表示0的点到点的距离是1,到点的距离是2,那么点就不是的“妙点”,但点是的“妙点”.
【知识应用】
如图②,,为数轴上两点,点表示的数为,点表示的数为4.
(1) 数3_ _ _ _ (填“是”或“不是”)的“妙点”,数2_ _ _ _ (填“是”或“不是”)的“妙点”.
(2) 若数轴上点表示的数为,且点是的“妙点”,求的值.
(3) 如图③,,为数轴上两点,点表示的数为,点表示的数为20.现有一只电子蚂蚁从点出发,以每秒2个单位长度的速度向左运动,到达点停止.设运动的时间为,当为何值时,点,,中恰有一个点为其余两点的“妙点”?(请直接写出答案)
第六章质量评估
一、选择题(本大题共10个小题,每小题3分,共30分)
1.C 2.A 3.C 4.C 5.B 6.D 7.D 8.B 9.A 10.D
二、填空题(本大题共6个小题,每小题3分,共18分)
11.45
12.北偏东; 南偏东
13.60
14.18
15.
16.(1) 15或
(2) 或
三、解答题(本大题共9个小题,共72分)
17.(1) 解:原式.
(2) 原式.
(3) 原式.
18.(1) 解:如答图,直线,线段,射线即为所求作.
第18题答图
(2) 如答图,线段即为所求作.
第18题答图
(3) 6
19.解: ,平分,
.
又 ,
.
平分,
,
.
20.(1) 解:无盖长方体盒子的平面示意图如答图所示.
第20题答图
(2) ;
(3)
21.(1) ; 4; 1.5
(2) 解:如答图,当点在线段的延长线上时,
第21题答图
,为线段的中点,
.
又,
.
22.(1) 7
(2) 解: 点也是线段的“三高四新点”(不同于点),
,即.
,
,.
,.
23.(1) 解:与互为余角,,
.
(2) ① 设 ,则 ,
与互为余角,
,即,解得.
.
② 由①知 .
与互为补角,
.
平分, ,
.
24.(1) ;
(2) 解: .理由如下.
, ,
.
平分,.
,
, .
(3) 不存在.
平分,
.
, ,
, .
25.(1) 不是; 不是
(2) 解:若点在,两点之间,则,
解得;
若点在点的左侧,则,
解得;
若点在点的右侧,则,
解得(不符合题意,舍去),
综上所述,的值为0或.
(3) 由题意,知,,,.
当点是的“妙点”时,则,
解得;
当点是的“妙点”时,则,
解得;
当点是的“妙点”时,则,
解得;
当点是的“妙点”时,则,
解得,不符合题意,舍去;
当点是的“妙点”时,则,
解得;
当点是的“妙点”时,则,
解得,不符合题意,舍去.
综上所述,当的值为10,20或15时,点,,中恰有一个点为其余两点的“妙点”.
[时间:120分钟 分值:120分]
一、选择题(本大题共10个小题,每小题3分,共30分)
1.如图是由几个完全相同的小正方体组成的一个几何体,这个几何体从左面看到的平面图形是( )
A. B.
C. D.
2.如图,已知同一平面内三点,,,画直线,画射线,连接,按照上述语句画图正确的是( )
A. B.
C. D.
3.下列说法不正确的有( )
①正方体有8个顶点和6个面;
②两个锐角的和一定大于 ;
③若,则是的平分线;
④两点之间,线段最短;
⑤钝角的补角一定大于这个角本身;
⑥射线也可以表示为射线.
A.2个 B.3个 C.4个 D.5个
4.如图,已知线段,是的中点,点在线段上,,那么线段的长为( )
A. B. C. D.
5.已知 与 互为余角,,则 的补角是( )
A. B. C. D.
6.已知线段,延长至点,使,反向延长至点,使,那么线段的长是线段长的( )
A. B. C. D.
7.如图,是的平分线,, ,则的度数是( )
A. B. C. D.
8.当钟表上显示12时15分时,时针与分针的夹角为( )
A. B. C. D.
9.如图,已知数轴上,,三点表示的数分别为,0,4,动点从点出发,沿数轴向右运动.在运动过程中,始终为的中点,始终为的中点,点在从点运动到点的过程中,则线段的长度为( )
A.6 B.5 C.4 D.3
10.如图,为直线上一点,为直角,平分,平分,平分,有下列结论:与互为余角; ;与互为补角; .其中正确的是( )
A.①②③④ B.③④ C.②③ D.②③④
二、填空题(本大题共6个小题,每小题3分,共18分)
11.单位换算:_ _ _ _ .
12.如图,射线表示_ _ _ _ _ _ _ _ _ _ _ _ 方向,射线表示_ _ _ _ _ _ _ _ _ _ _ _ 方向.
13.将一张长方形纸片按如图所示的方式折叠,,为折痕,点落在点处,点落在点处,且与重合.若 ,则的度数为_ _ _ _.
14.如图,已知线段,延长至点,使得,若是的中点,,则的长为_ _ _ _ .
15.若一个角的余角比这个角的补角的一半小 ,则这个角的度数为_ _ _ _ _ _ .
16.定义:把有公共顶点和一条公共边的两个角称为“共边角”.
(1) 当两个“共边角”为 和 时,它们非公共边的两边的夹角的度数为_ _ _ _ _ _ _ _ _ _ ;
(2) 若两个“共边角”非公共边的两边所成的角是 ,则这两个角的平分线的夹角度数为_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ .
三、解答题(本大题共9个小题,共72分)
17.(6分)计算:
(1) ;
(2) ;
(3) .
18.(6分)如图,在同一平面内有,,三点.
(1) 画直线,线段和射线;
(2) 在线段上任取一点(不同于点,),连接线段;
(3) 在(1),(2)的条件下,图中有_ _ _ _ 条线段.
19.(6分)如图,已知 , ,平分,平分,求和的度数.
20.(8分)如图①,有一块长方形纸板,长是宽的2倍.现将其四角各剪去一个正方形,折成如图②所示的高为的无盖长方体盒子(纸板厚度忽略不计).
(1) 请在图①中的长方形纸板中画出无盖长方体盒子的平面示意图,用实线表示剪切线,虚线表示折痕;
(2) 如果无盖长方体盒子底面宽为,长是宽的3倍,原长方形纸板的长可以用两个不同的代数式表示,则这两个代数式分别为_ _ _ _ _ _ _ _ _ _ 或_ _ _ _ _ _ _ _ _ _ ;
(3) 如果原长方形纸板的宽为,经过剪切折成的无盖长方体盒子底面的周长为_ _ _ _ _ _ _ _ _ _ .
21.(8分)阅读感悟:
数学课上,老师给出了如下问题:如图①,一条直线上有,,,四点,线段,为线段的中点,线段,请你补全图形,并求的长度.
以下是小华的解答过程:
解:如图②,
因为线段,为线段 的中点,
所以 _ _ _ _ _ _ _ _ .
因为,
所以 _ _ _ _ .
小斌认为这个题应该有两种情况,小华只考虑了点 在线段 上,事实上,点 还可以在线段 的延长线上.
解决问题:
(1) 请填空:将小华的解答过程补充完整;
(2) 根据小斌的想法,请你在备用图中画出另一种情况对应的示意图,并求出此时的长度.
22.(9分)定义:如果线段上的一个点将这条线段分成长度分别是,的两部分,并且满足,那么这个点叫作这条线段的“三高四新点”.
(1) 如图,点是线段的“三高四新点”,,且,则_ _ _ _ ;
(2) 若点也是(1)中线段的“三高四新点”(不同于点),求与的数量关系.
23.(9分)如图,与互为补角,与互为余角.
(1) 若,求的度数.
(2) 若.
① 求的度数;
② 如果平分,求的度数.
24.(10分)如图①, ,将三角板的直角顶点放置在点处,平分.
(1) 若 ,则_ _ _ _ _ _ ,_ _ _ _ _ _ .
(2) 若 , ,试判断 , 之间的数量关系,并说明理由.
(3) 如图②,当三角板绕着点顺时针旋转一定角度,使得在的内部,在的外部.若 , , , 是否还存在(2)中的数量关系?若存在,请说明理由;若不存在,请求出 , 的数量关系.
25.(10分)【阅读理解】
已知,,为数轴上三点,若点到点的距离是点到点的距离的2倍,我们就称点是的“妙点”.例如,如图①,点表示的数为,点表示的数为2,点表示的数为1,点到点的距离是2,到点的距离是1,那么点是的“妙点”.又例如,表示0的点到点的距离是1,到点的距离是2,那么点就不是的“妙点”,但点是的“妙点”.
【知识应用】
如图②,,为数轴上两点,点表示的数为,点表示的数为4.
(1) 数3_ _ _ _ (填“是”或“不是”)的“妙点”,数2_ _ _ _ (填“是”或“不是”)的“妙点”.
(2) 若数轴上点表示的数为,且点是的“妙点”,求的值.
(3) 如图③,,为数轴上两点,点表示的数为,点表示的数为20.现有一只电子蚂蚁从点出发,以每秒2个单位长度的速度向左运动,到达点停止.设运动的时间为,当为何值时,点,,中恰有一个点为其余两点的“妙点”?(请直接写出答案)
第六章质量评估
一、选择题(本大题共10个小题,每小题3分,共30分)
1.C 2.A 3.C 4.C 5.B 6.D 7.D 8.B 9.A 10.D
二、填空题(本大题共6个小题,每小题3分,共18分)
11.45
12.北偏东; 南偏东
13.60
14.18
15.
16.(1) 15或
(2) 或
三、解答题(本大题共9个小题,共72分)
17.(1) 解:原式.
(2) 原式.
(3) 原式.
18.(1) 解:如答图,直线,线段,射线即为所求作.
第18题答图
(2) 如答图,线段即为所求作.
第18题答图
(3) 6
19.解: ,平分,
.
又 ,
.
平分,
,
.
20.(1) 解:无盖长方体盒子的平面示意图如答图所示.
第20题答图
(2) ;
(3)
21.(1) ; 4; 1.5
(2) 解:如答图,当点在线段的延长线上时,
第21题答图
,为线段的中点,
.
又,
.
22.(1) 7
(2) 解: 点也是线段的“三高四新点”(不同于点),
,即.
,
,.
,.
23.(1) 解:与互为余角,,
.
(2) ① 设 ,则 ,
与互为余角,
,即,解得.
.
② 由①知 .
与互为补角,
.
平分, ,
.
24.(1) ;
(2) 解: .理由如下.
, ,
.
平分,.
,
, .
(3) 不存在.
平分,
.
, ,
, .
25.(1) 不是; 不是
(2) 解:若点在,两点之间,则,
解得;
若点在点的左侧,则,
解得;
若点在点的右侧,则,
解得(不符合题意,舍去),
综上所述,的值为0或.
(3) 由题意,知,,,.
当点是的“妙点”时,则,
解得;
当点是的“妙点”时,则,
解得;
当点是的“妙点”时,则,
解得;
当点是的“妙点”时,则,
解得,不符合题意,舍去;
当点是的“妙点”时,则,
解得;
当点是的“妙点”时,则,
解得,不符合题意,舍去.
综上所述,当的值为10,20或15时,点,,中恰有一个点为其余两点的“妙点”.
同课章节目录
