2.1.1 指数与指数幂的运算 课件(第2课时)
文档属性
| 名称 | 2.1.1 指数与指数幂的运算 课件(第2课时) |

|
|
| 格式 | zip | ||
| 文件大小 | 445.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-08-01 00:00:00 | ||
图片预览






文档简介
课件19张PPT。2.1.1指数与指数幂的运算(第二节)1.整数指数幂的概念
一、温故而知新2.整数指数幂的运算性质: 一、温故而知新n次方根的定义:
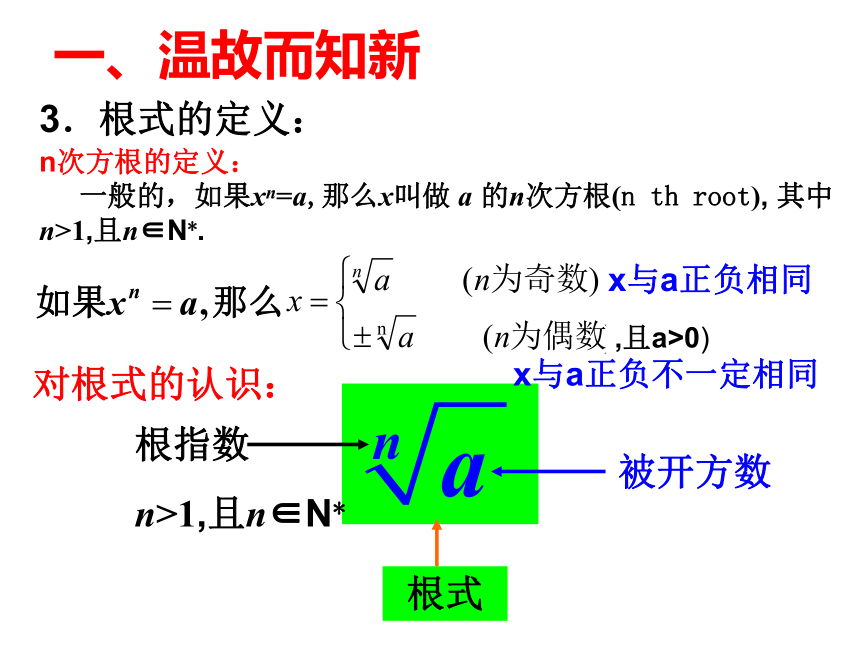
一般的,如果xn=a,那么x叫做 a 的n次方根(n th root), 其中n>1,且n∈N*.,且a>0)x与a正负相同x与a正负不一定相同对根式的认识:根指数
n>1,且n∈N*根式被开方数3.根式的定义: 一、温故而知新4.根式的运算性质: 一、温故而知新① 二、分数指数幂探究:(a>0)我们规定以下写法也成立:(a>0)(a>0)因此我们规定:正数的正分数指数幂的意义是 正数的负分数指数幂的意义与负整数幂的意义相同,
我们规定:
0的正分数指数幂等于0,
0的负分数指数幂无意义 。
注意:(1)根式与分数指数幂可以互化;
(2)指数的概念就从整数指数推广到了有理数指数.例1:用根式的形式表示下列各式(a>0): 整数指数幂的运算性质对于有理指数幂也同样适用,即对于任意有理数r,s,均有下面的运算性质:例2:用分数指数幂的形式表示下列各式(a>0):三、有理数指数幂的运算性质例3:计算下列各式(式中字母都是正数) 巩固练习课本54页练习1,2,3四、知识小结: 整数指数幂根式 两个等式 分数指数幂 有理数指数幂五、作业:59页A组:1,2,4 在前面的学习中,我们已经把正整数指数推广到了有理数指数,那么能不能推广到实数呢?(请同学们自己阅读课本53页) 无理数指数幂探究: 一般地,无理数指数幂 是一个确定的实数,有理数指数幂的运算性质同样适用于无理数指数幂。 其中的未知数都是非负数 练一练(6) ,下列各式总能成立的是( )B题型一:化简求值题型二:给值求值题型三:条件求值2、计算下式练一练4、化简 的结果是( )C5、2-(2k+1)-2-(2k-1)+2-2k等于( )
A.2-2k B. 2-(2k-1) C. -2-(2k+1) D.2C(-?,-1)?(1,+?)
一、温故而知新2.整数指数幂的运算性质: 一、温故而知新n次方根的定义:
一般的,如果xn=a,那么x叫做 a 的n次方根(n th root), 其中n>1,且n∈N*.,且a>0)x与a正负相同x与a正负不一定相同对根式的认识:根指数
n>1,且n∈N*根式被开方数3.根式的定义: 一、温故而知新4.根式的运算性质: 一、温故而知新① 二、分数指数幂探究:(a>0)我们规定以下写法也成立:(a>0)(a>0)因此我们规定:正数的正分数指数幂的意义是 正数的负分数指数幂的意义与负整数幂的意义相同,
我们规定:
0的正分数指数幂等于0,
0的负分数指数幂无意义 。
注意:(1)根式与分数指数幂可以互化;
(2)指数的概念就从整数指数推广到了有理数指数.例1:用根式的形式表示下列各式(a>0): 整数指数幂的运算性质对于有理指数幂也同样适用,即对于任意有理数r,s,均有下面的运算性质:例2:用分数指数幂的形式表示下列各式(a>0):三、有理数指数幂的运算性质例3:计算下列各式(式中字母都是正数) 巩固练习课本54页练习1,2,3四、知识小结: 整数指数幂根式 两个等式 分数指数幂 有理数指数幂五、作业:59页A组:1,2,4 在前面的学习中,我们已经把正整数指数推广到了有理数指数,那么能不能推广到实数呢?(请同学们自己阅读课本53页) 无理数指数幂探究: 一般地,无理数指数幂 是一个确定的实数,有理数指数幂的运算性质同样适用于无理数指数幂。 其中的未知数都是非负数 练一练(6) ,下列各式总能成立的是( )B题型一:化简求值题型二:给值求值题型三:条件求值2、计算下式练一练4、化简 的结果是( )C5、2-(2k+1)-2-(2k-1)+2-2k等于( )
A.2-2k B. 2-(2k-1) C. -2-(2k+1) D.2C(-?,-1)?(1,+?)
