空间向量数量积课件
图片预览





文档简介
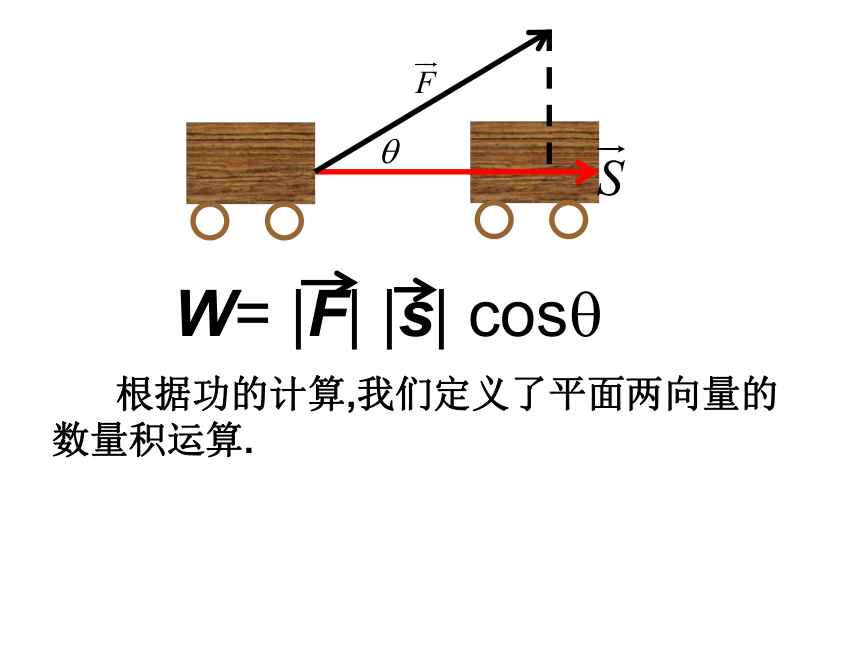
课件19张PPT。空间向量的数量积(1) 根据功的计算,我们定义了平面两向量的数量积运算.1.平面两个向量的夹角已知两个非零向量 , 作 则
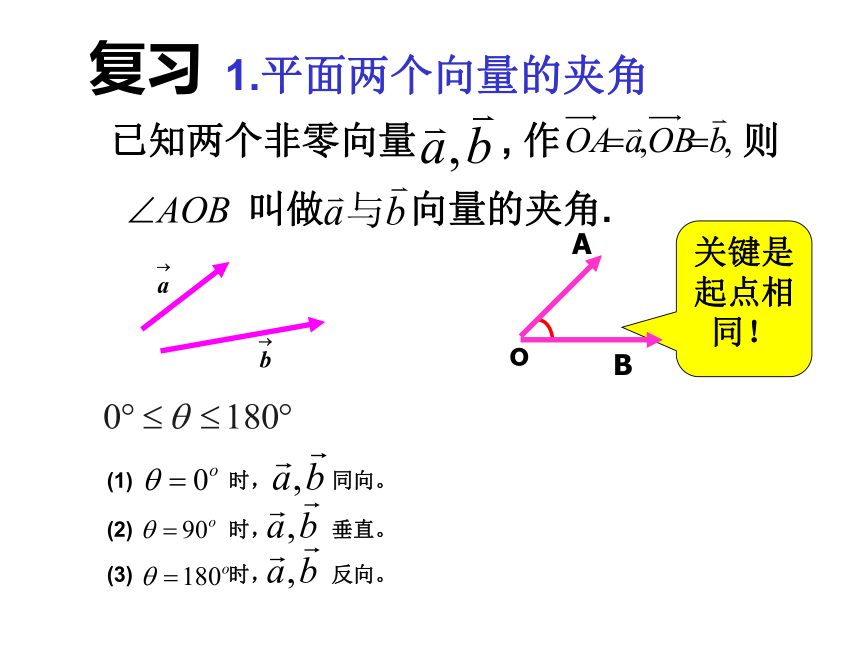
叫做 向量的夹角. o关键是起点相同!复习(1) 时, 同向。(2) 时, 垂直。(3) 时, 反向。2.平面两个向量的数量积规定:零向量与任一向量的数量积为0。两个向量的数量积是数量,而不是向量. 已知两个非零向量 ,它们的夹角为 ,
我们把 叫做向量 的数量积,
记作 ,即 。当_______时, 。当_______时, 。当_______时, 。3.平面向量数量积运算律 ⑴⑵⑶(数乘结合律) (分配律) (交换律) 注意:4.平面向量数量积的性质⑴⑵⑶ 变形求夹角垂直依据长度(模)对于非零向量 ,有:已知平面中
则 的夹角为 因为向量可以自由平移,所以空间
中任意两个向量可以平移到同一平面内,
即空间任意两个向量共面. 因此,平面
中两个向量的夹角及数量积等相关概念、
性质可以推广到空间.1. 两个向量的夹角已知两个非零向量 , 作 则
叫做 向量的夹角. 12.3关键是起点相同!复习新授平面空间记作:2. 两个向量的数量积已知两个非零向量 ,它们的夹角为
我们把 叫做向量 的
数量积,记做 ,即 = 两个向量的数量积是数量,而不是向量.注意:平面空间3. 向量数量积运算律 ⑴⑵⑶(数乘结合律) (分配律) (交换律) 空间平面注意:数量积不满足结合律4. 向量数量积的性质⑵⑶ 对于非零向量 ,有:变形求夹角判断垂直求长度(模)⑴平面空间1.若 ,则 或 ( ) 1.概念辨析:(已知 为非零向量)2. ( ) 3. ( )4.若 与 均不为零向量,则
它们垂直。 ( )√① ② ③ ④ ⑤E ① ⑤2.例:在平行六面体ABCD-A1B1C1D1中,AB=4,AD=4, AA1=5,∠BAD=90O,∠BAA1=∠DAA1=60O (1)求AC1的长 (2)求证: AA1⊥BD变式:在平行六面体ABCD-A1B1C1D1中,AB=4,AD=3,AA1=5,∠BAD=90O,∠BAA1=∠DAA1=60O 求:异面直线AA1与BD所成角的余弦值. 问:在线段AA1上是否存在一点M使得BM⊥AC1?
并求此点位置.引申:在平行六面体ABCD-A1B1C1D1中,AB=4,AD=4,AA1=5,∠BAD=90O,∠BAA1=∠DAA1=60O 练习:1.在三棱锥O-ABC中,已知侧棱
OA,OB,OC两两互相垂直,
求证:底面△ABC是锐角三角形..2如图,在平行四边形ABCD中,AB=AC=1,∠ACD=90o,将它沿对角线AC折起,使AB
与CD成60o,求B、D间的距离。
练习:空间向量数量积的定义 空间向量数量积的性质空间向量数量积的运用空间向量的夹角
叫做 向量的夹角. o关键是起点相同!复习(1) 时, 同向。(2) 时, 垂直。(3) 时, 反向。2.平面两个向量的数量积规定:零向量与任一向量的数量积为0。两个向量的数量积是数量,而不是向量. 已知两个非零向量 ,它们的夹角为 ,
我们把 叫做向量 的数量积,
记作 ,即 。当_______时, 。当_______时, 。当_______时, 。3.平面向量数量积运算律 ⑴⑵⑶(数乘结合律) (分配律) (交换律) 注意:4.平面向量数量积的性质⑴⑵⑶ 变形求夹角垂直依据长度(模)对于非零向量 ,有:已知平面中
则 的夹角为 因为向量可以自由平移,所以空间
中任意两个向量可以平移到同一平面内,
即空间任意两个向量共面. 因此,平面
中两个向量的夹角及数量积等相关概念、
性质可以推广到空间.1. 两个向量的夹角已知两个非零向量 , 作 则
叫做 向量的夹角. 12.3关键是起点相同!复习新授平面空间记作:2. 两个向量的数量积已知两个非零向量 ,它们的夹角为
我们把 叫做向量 的
数量积,记做 ,即 = 两个向量的数量积是数量,而不是向量.注意:平面空间3. 向量数量积运算律 ⑴⑵⑶(数乘结合律) (分配律) (交换律) 空间平面注意:数量积不满足结合律4. 向量数量积的性质⑵⑶ 对于非零向量 ,有:变形求夹角判断垂直求长度(模)⑴平面空间1.若 ,则 或 ( ) 1.概念辨析:(已知 为非零向量)2. ( ) 3. ( )4.若 与 均不为零向量,则
它们垂直。 ( )√① ② ③ ④ ⑤E ① ⑤2.例:在平行六面体ABCD-A1B1C1D1中,AB=4,AD=4, AA1=5,∠BAD=90O,∠BAA1=∠DAA1=60O (1)求AC1的长 (2)求证: AA1⊥BD变式:在平行六面体ABCD-A1B1C1D1中,AB=4,AD=3,AA1=5,∠BAD=90O,∠BAA1=∠DAA1=60O 求:异面直线AA1与BD所成角的余弦值. 问:在线段AA1上是否存在一点M使得BM⊥AC1?
并求此点位置.引申:在平行六面体ABCD-A1B1C1D1中,AB=4,AD=4,AA1=5,∠BAD=90O,∠BAA1=∠DAA1=60O 练习:1.在三棱锥O-ABC中,已知侧棱
OA,OB,OC两两互相垂直,
求证:底面△ABC是锐角三角形..2如图,在平行四边形ABCD中,AB=AC=1,∠ACD=90o,将它沿对角线AC折起,使AB
与CD成60o,求B、D间的距离。
练习:空间向量数量积的定义 空间向量数量积的性质空间向量数量积的运用空间向量的夹角
