1.1.2空间向量的数量积运算 学案(含答案)2025-2026学年高二上学期数学人教A版选择性必修第一册
文档属性
| 名称 | 1.1.2空间向量的数量积运算 学案(含答案)2025-2026学年高二上学期数学人教A版选择性必修第一册 |

|
|
| 格式 | docx | ||
| 文件大小 | 273.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-25 00:00:00 | ||
图片预览

文档简介
第一章 空间向量与立体几何
1.1.2·空间向量的数量积运算
学习指导
课标要求 核心素养 重难分析
1、掌握空间向量数量积的定义、运算律 2、能运用空间向量数量积解决空间中垂直、长度、角度等问题 3、体会空间向量数量积与平面向量数量积的联系与区别 通过从平面向量推广到空间向量,抽象出空间向量数量积的定义与运算律 重点 空间向量数量积的定义、运算律
利用数量积解决空间垂直、长度、角度问题
难点 空间向量数量积几何意义的深入理解
运用数量积解决复杂的空间几何问题
知识清单
知识点一 空间向量的数量积
1.空间向量的夹角:已知两个非零向量a,b,在空间任取一点O,令,,则叫做向量a,b的夹角,记作__________.
若,则向量a,b__________,记作.
2.空间向量的数量积:已知两个非零向量a,b,则__________叫做a,b的数量积,记作__________,即.
特别地,零向量与任意向量的数量积为__________.
由向量的数量积定义得到:__________;__________.
3.向量的投影:向量a向向量b投影,得到与向量b__________的向量c,__________,则向量c称为向量a在向量b上的投影向量.
4.空间向量数量积的运算律:
(1)__________,;
(2)(交换律);
(3)__________(分配律).
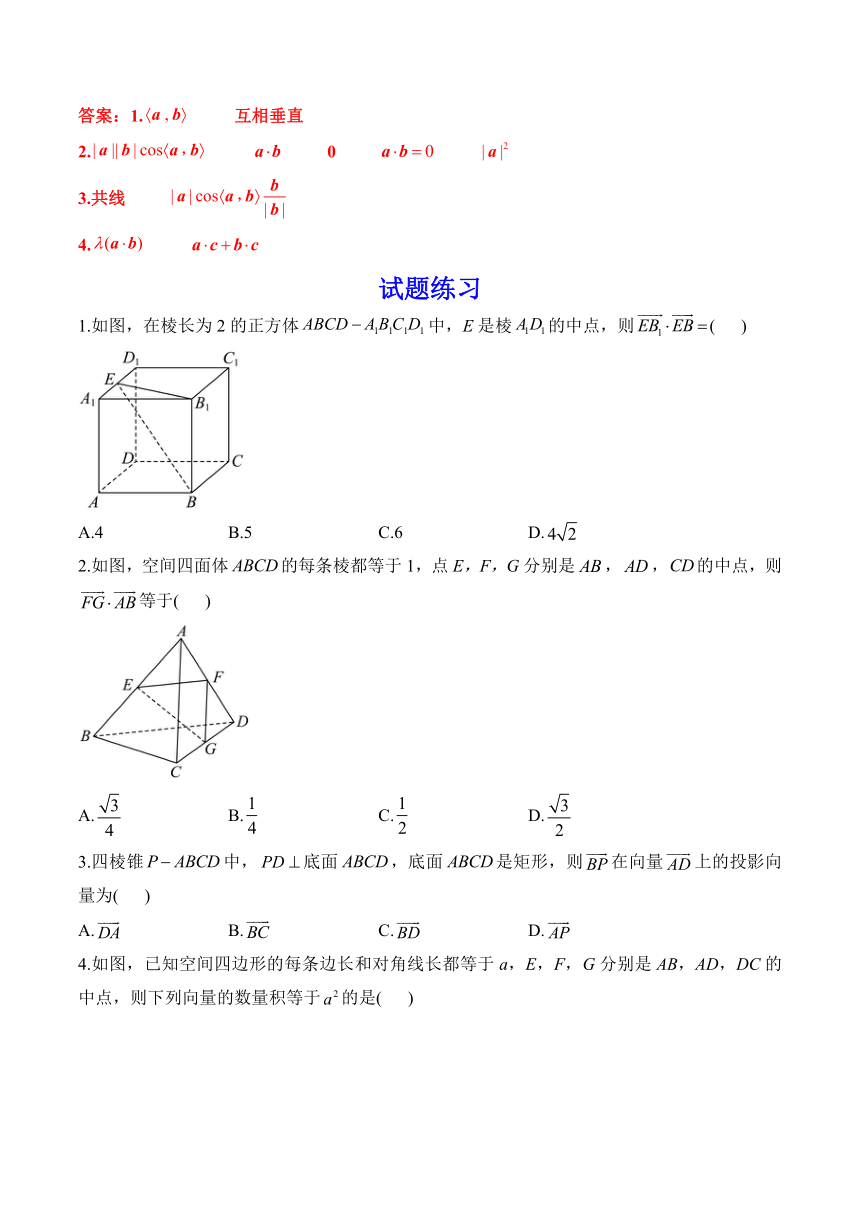
答案:1. 互相垂直
2. 0
3.共线
4.
试题练习
1.如图,在棱长为2的正方体中,E是棱的中点,则( )
A.4 B.5 C.6 D.
2.如图,空间四面体的每条棱都等于1,点E,F,G分别是,,的中点,则等于( )
A. B. C. D.
3.四棱锥中,底面,底面是矩形,则在向量上的投影向量为( )
A. B. C. D.
4.如图,已知空间四边形的每条边长和对角线长都等于a,E,F,G分别是AB,AD,DC的中点,则下列向量的数量积等于的是( )
A. B. C. D.
5.在棱长为2的正方体中,M为棱上任意一点,则________.
答案以及解析
1.答案:B
解析:
.
故选:B.
2.答案:B
解析:,.
故选:B.
3.答案:B
解析:四棱锥如图所示,
底面是矩形,∴,
底面,底面,∴,
过向量的始点B作直线的垂线,垂足为点A,
过向量的终点P作直线的垂线,
垂足为点D,在向量上的投影向量为,
由底面是矩形,,
故选:B.
4.答案:B
解析:由题意得,与,与的夹角均为,与的夹角为,与的夹角为0,故,,,,故选B.
5.答案:4
解析:棱长为2的正方体如图所示,
.
1.1.2·空间向量的数量积运算
学习指导
课标要求 核心素养 重难分析
1、掌握空间向量数量积的定义、运算律 2、能运用空间向量数量积解决空间中垂直、长度、角度等问题 3、体会空间向量数量积与平面向量数量积的联系与区别 通过从平面向量推广到空间向量,抽象出空间向量数量积的定义与运算律 重点 空间向量数量积的定义、运算律
利用数量积解决空间垂直、长度、角度问题
难点 空间向量数量积几何意义的深入理解
运用数量积解决复杂的空间几何问题
知识清单
知识点一 空间向量的数量积
1.空间向量的夹角:已知两个非零向量a,b,在空间任取一点O,令,,则叫做向量a,b的夹角,记作__________.
若,则向量a,b__________,记作.
2.空间向量的数量积:已知两个非零向量a,b,则__________叫做a,b的数量积,记作__________,即.
特别地,零向量与任意向量的数量积为__________.
由向量的数量积定义得到:__________;__________.
3.向量的投影:向量a向向量b投影,得到与向量b__________的向量c,__________,则向量c称为向量a在向量b上的投影向量.
4.空间向量数量积的运算律:
(1)__________,;
(2)(交换律);
(3)__________(分配律).
答案:1. 互相垂直
2. 0
3.共线
4.
试题练习
1.如图,在棱长为2的正方体中,E是棱的中点,则( )
A.4 B.5 C.6 D.
2.如图,空间四面体的每条棱都等于1,点E,F,G分别是,,的中点,则等于( )
A. B. C. D.
3.四棱锥中,底面,底面是矩形,则在向量上的投影向量为( )
A. B. C. D.
4.如图,已知空间四边形的每条边长和对角线长都等于a,E,F,G分别是AB,AD,DC的中点,则下列向量的数量积等于的是( )
A. B. C. D.
5.在棱长为2的正方体中,M为棱上任意一点,则________.
答案以及解析
1.答案:B
解析:
.
故选:B.
2.答案:B
解析:,.
故选:B.
3.答案:B
解析:四棱锥如图所示,
底面是矩形,∴,
底面,底面,∴,
过向量的始点B作直线的垂线,垂足为点A,
过向量的终点P作直线的垂线,
垂足为点D,在向量上的投影向量为,
由底面是矩形,,
故选:B.
4.答案:B
解析:由题意得,与,与的夹角均为,与的夹角为,与的夹角为0,故,,,,故选B.
5.答案:4
解析:棱长为2的正方体如图所示,
.
