高斯函数图像及性质与典型问题 讲义 2026届高三数学一轮复习
文档属性
| 名称 | 高斯函数图像及性质与典型问题 讲义 2026届高三数学一轮复习 |

|
|
| 格式 | docx | ||
| 文件大小 | 364.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-26 00:00:00 | ||
图片预览




文档简介
高斯函数图像及性质与典型问题
一、高斯函数及其性质
[x]表示不大于x的最大整数,如[3.9]=3,[0]=0,[-1.2]=-2,[6]=6
记{x}=x-[x],如{3.9}=0.9,{0}=0,{-1.2}=0.8,{6}=0;将函数f(x)=[x]
(x)叫做高斯函数,又称为取整函数。从定义出发,不难得到
[x]及{x}如下的一些性质:
(1) 对x, x-1 <[x] ≤x<[x]+1; 特别地,[n]=n(nZ)。
(2)对x, 函数y={x}的值域为[0,1);该结论可由(1)得到,特别地,{n}=0(nZ);
(3) nZ,x,则有[x+n]=[x]+n, {x+n}={x};
事实上,[x+n]=[([x]+n)+{x}]=[x]+n, {x+n}=x+n-[x+n]=x+n-[x]-n=x-[x]={x};
∴函数y={x}是周期函数,最小正周期T=1.
x,y,则有[x]+[y]≤[x+y]≤[x]+[y]+1;
事实上,[x+y]=[([x]+{x})+([y]+{y}]=[([x]+[y])+({x}+{y})]=[x]+[y]+[{x}+{y}]
∵0≤{x}<1,0≤{y}<1,∴0≤{x}+{y}<2,
∴[{x}+{y}]的可能取值为0或1,
得[x+y]=[x]+[y]或[x]+[y]+1,
即[x]+[y]≤[x+y]≤[x]+[y]+1;
n N+,x,则有[nx]≥n[x]; [nx]≤n[x]+n-1;
事实上,由(4)得[x+y]≥[x]+[y]得 ≥
即[nx]≥n[x];
函数f(x)=[x](x)是一个不减函数,即x1≤x2,则[x1]≤[x2];
事实上,当x1 ,x2[n,n+1)时,则[x1]=[x2]=n;
当x1 [n,n+1),x2≥n+1时,[x1]=n,[x2]≥n+1,则[x1]≤[x2].
综上所述当x1≤x2时,则[x1]≤[x2].
nN+x,则[1,x]内,恰好有[]个整数是n的倍数;
方法一、事实上, [] ≤ <[]+1, 即n[] ≤x∴[1,x]内,不超过x且是n的倍数的所有整数为:
[]n ,([]-1)n,([]-2)n,……,n;共计[]个。
方法二、设[1,x]内,恰好有k个整数是n的倍数。
则这些整数为n,2n,3n,……,kn; x满足kn≤x<(k+1)n,
∴∴[1,x]内,不超过x且是n的倍数的所有整数共计[]个。
x,y , {x+y} ≤{x}+{y};
事实上,{x+y} =x+y-[x+y]
{x}+{y}=x-[x]+y-[y]=x+y-([x]+[y])
∵[x]+[y]≤[x+y], ∴ {x+y} ≤{x}+{y}.
nN+,x,则有{nx}≤n{x};
事实上,∵n N+,x,得[nx]≥n[x];
∴nx-{nx}≥n(x-{x})=nx-n{x}, 即{nx}≤n{x};
x,y,[xy]≥[x][y];
由{x}{y}.,得x≥[x]>0, y≥[y]>0, xy≥[x][y]>0, ∴[xy]≥[x][y]。
备注: x,y,{xy}≤ {x} {y}不一定成立.
如取x=2.1,y=3.1,则xy=6.51,{xy}=0.51,{x}{y}=0.10.1=0.01,
此时{xy}>{x}{y}.
如取x=0.7,y=0.6,则xy=0.42,{xy}=0.42,{x}{y}=0.70.6=0.42,
此时{xy}={x}{y}.
如取x=5,y=6,则xy=30,{xy}=0,{x}{y}=00=0,此时{xy}={x}{y}.
如取x=y=1.9,则xy=3.61,{xy}=0.61,{x}{y}=0.90.9=0.81,
此时{xy}<{x}{y}.
高斯函数及相关函数的图像
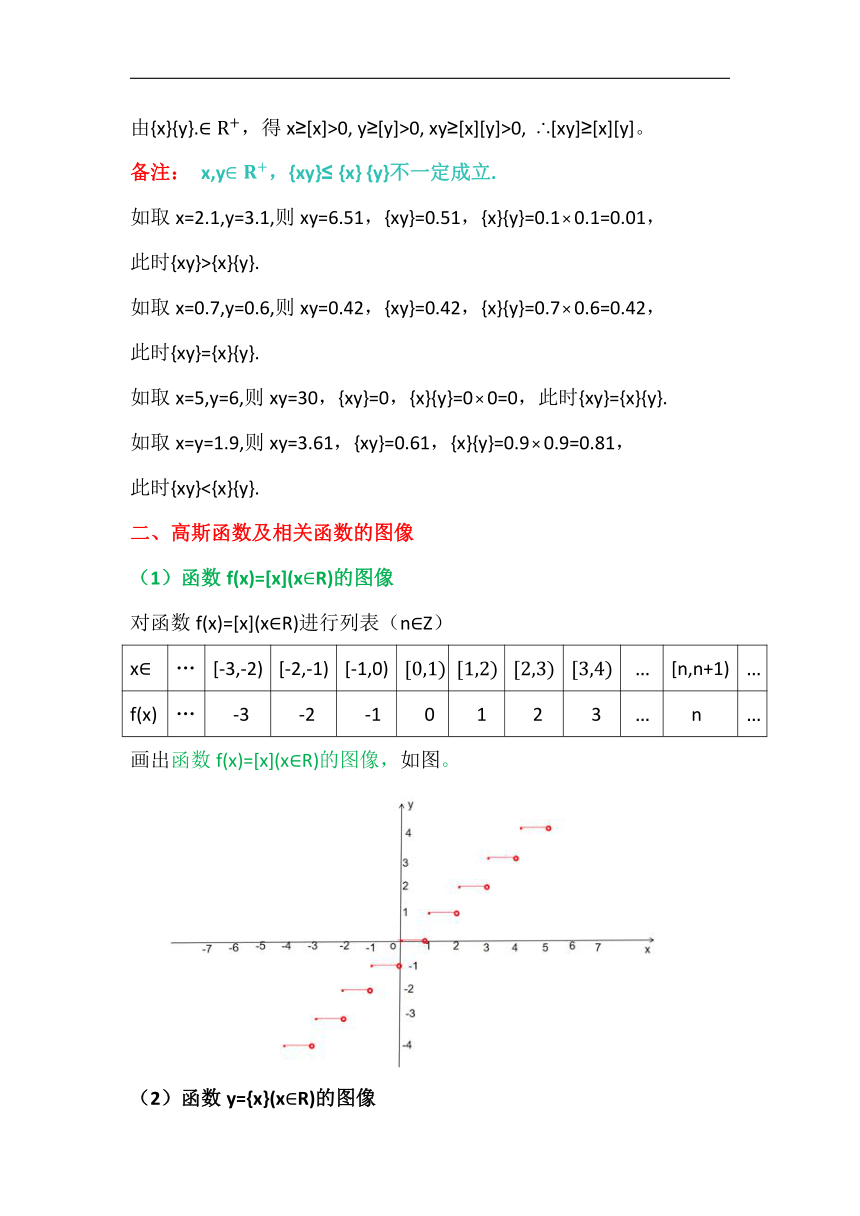
(1)函数f(x)=[x](xR)的图像
对函数f(x)=[x](xR)进行列表(nZ)
x … [-3,-2) [-2,-1) [-1,0) [n,n+1)
f(x) … -3 -2 -1 0 1 2 3 n
画出函数f(x)=[x](xR)的图像,如图。
(2)函数y={x}(xR)的图像
对函数y={x}(xR)进行列表(nZ)
x … [-3,-2) [-2,-1) [-1,0) [n,n+1)
y … x+3 x+2 x+1 x x-1 x-2 x-3 x-n
画出函数y={x}(xR)的图像,如图。
(3)函数h(x)=[x]+[2x](xR)的图像
先分析函数h(x)=[x]+[2x](x)
h(x)=
由于h(x+1)=[x+1]+[2x+2]=[x]+1+[2x]+2=h(x)+3,
得出函数h(x)=[x]+[2x](xR)的图像,如图:
(4)函数m(x)=[x]+[2x]+[3x](xR)的图像
先分析函数m(x)=[x]+[2x]+[3x](x)
由于m(x+1)=[x+1]+[2x+2]+[3x+3]=[x]+1+[2x]+2+[3x]+3=h(x)+6,
得出函数m(x)=[x]+[2x]+[3x](xR)的图像,如图:
(5)函数f(x)={x}+{2x}(xR)的图像
函先分析数f(x)={x}+{2x}(x)的图像
f(x)=
事实上,时,{x}=x, 0≤2x<1,∴{2x}=2x, 得f(x)={x}+{2x}=x+2x=3x;
时,{x}=x,1≤2x<2,∴{2x}=2x-1, 得f(x)={x}+{2x}=x+2x-1=3x-1;
由于f(x+1)={x+}+{2x+2}={x}+{2x}=f(x),∴函数f(x)为周期函数,周期T=1,
从而得出函数f(x)={x}+{2x}(xR)的图像。
(6)函数g(x)={x}+{2x}+{3X}(xR)的图像
先分析g(x)={x}+{2x}+{3X}(x)
∵g(x+1)={x+1}+{2x+2}+{3x+3}={x}+{2x}+{3X}=g(x)
∴函数g(x)为周期函数,周期T=1。
得出函数g(x)={x}+{2x}+{3X}(xR)的图像,如图:
函数y=[-x](xR)的图像
可由函数y=[-x](xR)与y=[x](xR)的图像对称性得到,如图:
函数y={-x}(xR)的图像
可由函数y={-x}(xR)与y={x}(xR)的图像对称性得到,如图:
三、高斯函数相关问题
1.已知函数 -m(x>0),
若函数有且只有3个零点,求实数m的取值范围。
解析:
方法一:由题意0得[x]=mx,即方程[x]=mx (x>0)有且只有3个实数根;令y=[x],则函数y=[x]的图像与直线y=mx (x>0)有且只有3个公共点,如图,得
即实数m的取值范围为(]。
方法二:由题意0得[x]=mx,∴x-{x}=mx,即方程{x}=(1-m)x (x>0)有且只有3个实数根;当m=1时,方程化为{x}=0,此方程有无穷多个解,不合要求,∴m≠1。
令y={x},则函数y={x}的图像与直线y=(1-m)x (x>0)有且只有3个公共点,
∴ 解得
即实数m的取值范围为(]。
2.已知方程-[x]=ax2-x+1有且只有2个实数根,求实数a的取值范围。
解析:由题意-[x]=ax2-x+1得x-[x]=ax2+1,∴方程{x}=ax2+1有且只有2个实数根;当a=0时,方程化为{x}=1,此方程没有实数根,不合要求,
∴a≠0。
令y={x},则函数y={x}的图像与抛物线y=ax2+1 有且只有2个公共点;当a>0时,两个图像没有公共点,不合要求,∴a<0。
当a=-1时,两个图像有3个公共点,不合要求;
以下为两个图像有且只有2个公共点时的两种情况,如图所示:
当函数y={x}(x<0)的图像与抛物线y=ax2+1有且只有1公共点,并且函数y={x}(x≥0)的图像与抛物线y=ax2+1有且只有1公共点时,
如图(1)所示,
即函数y=x+1(x)的图像与抛物线y=ax2+1有且只有1个公共点(),函数y=x(x)的图像与抛物线y=ax2+1有且只有1个公共点,函数y=x-1(x)的图像与抛物线y=ax2+1没有公共点,∴-1<<0,
解得a<-1;
(2)当函数y={x}(x<0)的图像与抛物线y=ax2+1没有公共点,并且函数y={x}(x≥0)的图像与抛物线y=ax2+1有且只有2公共点时,如图(2)所示,
针对抛物线y=ax2+1与函数y=x+2(x)的图像没有公共点时的情况,首先要得出抛物线y=ax2+1与直线y=x+2相切时实数a的值,
由 得ax2-x-1=0,由⊿=1+4a=0得a=- ,
即当a=- 时抛物线y=ax2+1与直线y=x+2相切,切点恰为为(-2,0),当a<- 时抛物线y=ax2+1与直线y=x+2没有公共点;
因此由抛物线的对称性得,
解得-1综上所述实数a的取值范围为.
3.求方程x +1实数解的个数。
解析:令t(t>0),则原方程化为lnt+1 ∴t-{t}=lnt+1,
即方程{t}=t-lnt-1(t>0)的实数解的个数就是原方程实数解的个数。
令f(t)={t}(t>0), g(t)=t-lnt-1(t>0), F(t)= g(t)-f(t)(t>0),
∵(t)=1-=, ∴当t时,(t)<0,g(t)单调递减,当t时,(t)>0,g(t)单调递增,当t=1时g(t)取得最小值g(1)=0;如图所示,
显然,函数f(t)={t}的图像与g(t)=t-lnt-1的图像在有且只有两个公共点;
当t时,f(t)=t-1,F(t)= g(t)-f(t)=t-lnt-1-(t-1)=-lnt<0,
∴F(t)没有零点;
当t时,f(t)=t-2,F(t)= g(t)-f(t)=t-lnt-1-(t-2)=1-lnt,
F(2)=1-ln2>0,
F(2.8)=1-ln2.8<0,∴F(t)在上存在唯一的零点,∵(t)= - <0,
∴F(t)在上单调递减,F(t)在上恒小于零,不存在零点
∴F(t)在上有且只有一个零点;
当t时,f(t)=t-3, F(t)= g(t)-f(t)=t-lnt-1-(t-3)=2-lnt,
∵3≤t<4, ln3≤lnt∴0<2-ln4∴F(t)在上没有零点;
∵g(4)-1=4-ln4-1-1=2-ln4>0,∴g(4)>1;∵t>4时,函数 g(t)单调递增,
∴当t≥4时,g(t)≥g(4)>1,函数 g(t)的图像与函数f(t)的图像不再有公共点;
综上所述方程x +1实数解的个数为3.
4.求函数 的值域。
解析:
方法一:令=k,得方程{x}=kx(x≠0)有实数解, 即函数y={x}与函数y=kx(x≠0)的图像有公共点,如图所示,得到两个图像有公共点时的三种不同情况:
K<0时,两个图像总有公共点;k=1时两个图像有完全重合的部分,有无数个公共点;0≤k<时两个图像有公共点;
而当k>1或≤k<1时,两个图像显然没有公共点。
综上所述k的取值范围为{k|k=1或k<},即函数 的值域为
{1}U(-)。
方法二:
= =1-
当x<0时,{x}≥0,∴≤0; x时,=- ,
==1- =1+,当x时,-;
x时,==1,
x时,=1- =1- <1- = ,
x时,=1- =1- <1- = ,
……
x时,=1- =1- <1- = >0,
……
综上所述函数 的值域为{1}U(-)。
方法三
= =1-
令1- =m,得方程[x]=(1-m)x(x≠0)有实数解,即函数y=[x]与函数y=(1-m)x(x≠0)的图像有公共点,如图所示,得到两个图像有公共点时的三种不同情况:
当1-m=0或1-m≥1或 <1-m<1时两个图像有公共点,
即m=1或0≤m<时两个图像有公共点;
综上所述函数 的值域为{1}U(-)。
5.已知a<0,若方程{x}+{2x}- =a(x-)(x≥0)有且只有2个实数根,求实数a的取值范围。
解析:由题意得,函数y={x}+{2x}与函数y=a(x-)+(x≥0)的图像有且只有2个公共点,如图所示,
得-1即实数a的取值范围为(-1,0)。
6.若关于x的方程2{x}=2+logax(a>0,a≠1)有且只有2个实数根,求实数a的取值范围。
解析:由题意得函数y=2{x}(x>0)与函数y=2+logax(x>0)的图像有且只有2个公共点,如图所示,
得2+loga2≥0且2+loga3<0,解得;
即实数a的取值范围为(,]。
7.解方程[x]+[2x]=6.
解: x为不大于0的数时不适合原方程;∵[2x]≥2[x],
∴3[x]≤6,得[x]≤2,∴[x]=1或2;
当[x]=1时,1≤x<2,2≤2x<4,得[2x]=2或3,[x]+[2x]≠6;
当[x]=2时,由原方程得[2x]=4,∴4≤2x<5,令x=2+(0≤<1),则4≤2x=4+2<5, ∴0≤<, 即2≤<.
经验证2≤<是原方程的解,
∴原方程的解为2≤<。
8.求方程[5x+3]=4x+ 的所有解的和.
解:令t=5x+3,则x=,原方程化为[t]= + .
∴t-{t}= + ,即{t}=t+ ;
画出函数y={t}与y=t+的图像得方程{t}=t+有四个实数根,分别在(-4,-3),(-3,-2),(-2,-1),(-1,0)上;
当t(-4,-3)时,t-(-4)=t+ ,解得t=- , ∴x=- ;
当t(-3,-2)时,t-(-3)=t+ ,解得t=- , ∴x=- ;
当t(-2,-1)时,t-(-2)=t+ ,解得t=- , ∴x=- ;
当t(-1,0)时,t-(-1)=t+ ,解得t=- , ∴x=- ;
∴原方程的所有解的和为- - - - =-4.
9.已知函数,求函数的值域。
解析: = = =5 - +
= - ;
由0<<5得<<,
即函数的值域为{0,1,2,3,4,5 }.
10.数列{}中,= ,=-+1,
求[ + +……+]
解析:由=-+1得
-1=(-1),由=>1 ,得>1;
∴ = = - ,
= - ,
= - ,
= - ,
…………
= - ,
∴ = - ( + +……+),
得 + +……+= - < = 2,
+ +……+> + = + = >1,
∴[ + +……+]=1.
11.数列{}满足=0,=,数列{}满足{}=
(1)求,,的值,并证明数列{}是等比数列.
(2)设,求数列{}的前2n项和。
解析:(1)=2=0,=+2=2,=2=4,=+2=6,
∴=+2=2,=+2=4,=+2=8;
=+2=+4=2+4=2(+2)=2,
∴数列{}是公比为2的等比数列.
由(1)得=,=[],
n为偶数时,
=,
=[]=[]
=[ ]
=;
∴3==-1
∴=;
n为奇数时,=.
=[]=[]
=-+-+……+-]
=-+-+……+-1,
∴3(+1)=-+-+……+3,
3(+1)-1=-+-+……+3-==,
∴=-1= ;
即= 。
数列{}的前2n项和
=+++……+=(++……+)+(++……+)
=(++……+)+(++……+)
= += 。
=;
求:[]
解析:由=(k;
得= ==
==
=+ ]
=+ ]
=+ )。
当n为偶数时
=
+ - - + + +……++ )
=+ )= ;
[]
=[]=[]=[1+]=1;
当n为奇数时
=
+ - - + + +……- - )
=- )=0;
[]=0;
综上所述[]的值为0,或1。
一、高斯函数及其性质
[x]表示不大于x的最大整数,如[3.9]=3,[0]=0,[-1.2]=-2,[6]=6
记{x}=x-[x],如{3.9}=0.9,{0}=0,{-1.2}=0.8,{6}=0;将函数f(x)=[x]
(x)叫做高斯函数,又称为取整函数。从定义出发,不难得到
[x]及{x}如下的一些性质:
(1) 对x, x-1 <[x] ≤x<[x]+1; 特别地,[n]=n(nZ)。
(2)对x, 函数y={x}的值域为[0,1);该结论可由(1)得到,特别地,{n}=0(nZ);
(3) nZ,x,则有[x+n]=[x]+n, {x+n}={x};
事实上,[x+n]=[([x]+n)+{x}]=[x]+n, {x+n}=x+n-[x+n]=x+n-[x]-n=x-[x]={x};
∴函数y={x}是周期函数,最小正周期T=1.
x,y,则有[x]+[y]≤[x+y]≤[x]+[y]+1;
事实上,[x+y]=[([x]+{x})+([y]+{y}]=[([x]+[y])+({x}+{y})]=[x]+[y]+[{x}+{y}]
∵0≤{x}<1,0≤{y}<1,∴0≤{x}+{y}<2,
∴[{x}+{y}]的可能取值为0或1,
得[x+y]=[x]+[y]或[x]+[y]+1,
即[x]+[y]≤[x+y]≤[x]+[y]+1;
n N+,x,则有[nx]≥n[x]; [nx]≤n[x]+n-1;
事实上,由(4)得[x+y]≥[x]+[y]得 ≥
即[nx]≥n[x];
函数f(x)=[x](x)是一个不减函数,即x1≤x2,则[x1]≤[x2];
事实上,当x1 ,x2[n,n+1)时,则[x1]=[x2]=n;
当x1 [n,n+1),x2≥n+1时,[x1]=n,[x2]≥n+1,则[x1]≤[x2].
综上所述当x1≤x2时,则[x1]≤[x2].
nN+x,则[1,x]内,恰好有[]个整数是n的倍数;
方法一、事实上, [] ≤ <[]+1, 即n[] ≤x
[]n ,([]-1)n,([]-2)n,……,n;共计[]个。
方法二、设[1,x]内,恰好有k个整数是n的倍数。
则这些整数为n,2n,3n,……,kn; x满足kn≤x<(k+1)n,
∴
x,y , {x+y} ≤{x}+{y};
事实上,{x+y} =x+y-[x+y]
{x}+{y}=x-[x]+y-[y]=x+y-([x]+[y])
∵[x]+[y]≤[x+y], ∴ {x+y} ≤{x}+{y}.
nN+,x,则有{nx}≤n{x};
事实上,∵n N+,x,得[nx]≥n[x];
∴nx-{nx}≥n(x-{x})=nx-n{x}, 即{nx}≤n{x};
x,y,[xy]≥[x][y];
由{x}{y}.,得x≥[x]>0, y≥[y]>0, xy≥[x][y]>0, ∴[xy]≥[x][y]。
备注: x,y,{xy}≤ {x} {y}不一定成立.
如取x=2.1,y=3.1,则xy=6.51,{xy}=0.51,{x}{y}=0.10.1=0.01,
此时{xy}>{x}{y}.
如取x=0.7,y=0.6,则xy=0.42,{xy}=0.42,{x}{y}=0.70.6=0.42,
此时{xy}={x}{y}.
如取x=5,y=6,则xy=30,{xy}=0,{x}{y}=00=0,此时{xy}={x}{y}.
如取x=y=1.9,则xy=3.61,{xy}=0.61,{x}{y}=0.90.9=0.81,
此时{xy}<{x}{y}.
高斯函数及相关函数的图像
(1)函数f(x)=[x](xR)的图像
对函数f(x)=[x](xR)进行列表(nZ)
x … [-3,-2) [-2,-1) [-1,0) [n,n+1)
f(x) … -3 -2 -1 0 1 2 3 n
画出函数f(x)=[x](xR)的图像,如图。
(2)函数y={x}(xR)的图像
对函数y={x}(xR)进行列表(nZ)
x … [-3,-2) [-2,-1) [-1,0) [n,n+1)
y … x+3 x+2 x+1 x x-1 x-2 x-3 x-n
画出函数y={x}(xR)的图像,如图。
(3)函数h(x)=[x]+[2x](xR)的图像
先分析函数h(x)=[x]+[2x](x)
h(x)=
由于h(x+1)=[x+1]+[2x+2]=[x]+1+[2x]+2=h(x)+3,
得出函数h(x)=[x]+[2x](xR)的图像,如图:
(4)函数m(x)=[x]+[2x]+[3x](xR)的图像
先分析函数m(x)=[x]+[2x]+[3x](x)
由于m(x+1)=[x+1]+[2x+2]+[3x+3]=[x]+1+[2x]+2+[3x]+3=h(x)+6,
得出函数m(x)=[x]+[2x]+[3x](xR)的图像,如图:
(5)函数f(x)={x}+{2x}(xR)的图像
函先分析数f(x)={x}+{2x}(x)的图像
f(x)=
事实上,时,{x}=x, 0≤2x<1,∴{2x}=2x, 得f(x)={x}+{2x}=x+2x=3x;
时,{x}=x,1≤2x<2,∴{2x}=2x-1, 得f(x)={x}+{2x}=x+2x-1=3x-1;
由于f(x+1)={x+}+{2x+2}={x}+{2x}=f(x),∴函数f(x)为周期函数,周期T=1,
从而得出函数f(x)={x}+{2x}(xR)的图像。
(6)函数g(x)={x}+{2x}+{3X}(xR)的图像
先分析g(x)={x}+{2x}+{3X}(x)
∵g(x+1)={x+1}+{2x+2}+{3x+3}={x}+{2x}+{3X}=g(x)
∴函数g(x)为周期函数,周期T=1。
得出函数g(x)={x}+{2x}+{3X}(xR)的图像,如图:
函数y=[-x](xR)的图像
可由函数y=[-x](xR)与y=[x](xR)的图像对称性得到,如图:
函数y={-x}(xR)的图像
可由函数y={-x}(xR)与y={x}(xR)的图像对称性得到,如图:
三、高斯函数相关问题
1.已知函数 -m(x>0),
若函数有且只有3个零点,求实数m的取值范围。
解析:
方法一:由题意0得[x]=mx,即方程[x]=mx (x>0)有且只有3个实数根;令y=[x],则函数y=[x]的图像与直线y=mx (x>0)有且只有3个公共点,如图,得
即实数m的取值范围为(]。
方法二:由题意0得[x]=mx,∴x-{x}=mx,即方程{x}=(1-m)x (x>0)有且只有3个实数根;当m=1时,方程化为{x}=0,此方程有无穷多个解,不合要求,∴m≠1。
令y={x},则函数y={x}的图像与直线y=(1-m)x (x>0)有且只有3个公共点,
∴ 解得
即实数m的取值范围为(]。
2.已知方程-[x]=ax2-x+1有且只有2个实数根,求实数a的取值范围。
解析:由题意-[x]=ax2-x+1得x-[x]=ax2+1,∴方程{x}=ax2+1有且只有2个实数根;当a=0时,方程化为{x}=1,此方程没有实数根,不合要求,
∴a≠0。
令y={x},则函数y={x}的图像与抛物线y=ax2+1 有且只有2个公共点;当a>0时,两个图像没有公共点,不合要求,∴a<0。
当a=-1时,两个图像有3个公共点,不合要求;
以下为两个图像有且只有2个公共点时的两种情况,如图所示:
当函数y={x}(x<0)的图像与抛物线y=ax2+1有且只有1公共点,并且函数y={x}(x≥0)的图像与抛物线y=ax2+1有且只有1公共点时,
如图(1)所示,
即函数y=x+1(x)的图像与抛物线y=ax2+1有且只有1个公共点(),函数y=x(x)的图像与抛物线y=ax2+1有且只有1个公共点,函数y=x-1(x)的图像与抛物线y=ax2+1没有公共点,∴-1<<0,
解得a<-1;
(2)当函数y={x}(x<0)的图像与抛物线y=ax2+1没有公共点,并且函数y={x}(x≥0)的图像与抛物线y=ax2+1有且只有2公共点时,如图(2)所示,
针对抛物线y=ax2+1与函数y=x+2(x)的图像没有公共点时的情况,首先要得出抛物线y=ax2+1与直线y=x+2相切时实数a的值,
由 得ax2-x-1=0,由⊿=1+4a=0得a=- ,
即当a=- 时抛物线y=ax2+1与直线y=x+2相切,切点恰为为(-2,0),当a<- 时抛物线y=ax2+1与直线y=x+2没有公共点;
因此由抛物线的对称性得,
解得-1
3.求方程x +1实数解的个数。
解析:令t(t>0),则原方程化为lnt+1 ∴t-{t}=lnt+1,
即方程{t}=t-lnt-1(t>0)的实数解的个数就是原方程实数解的个数。
令f(t)={t}(t>0), g(t)=t-lnt-1(t>0), F(t)= g(t)-f(t)(t>0),
∵(t)=1-=, ∴当t时,(t)<0,g(t)单调递减,当t时,(t)>0,g(t)单调递增,当t=1时g(t)取得最小值g(1)=0;如图所示,
显然,函数f(t)={t}的图像与g(t)=t-lnt-1的图像在有且只有两个公共点;
当t时,f(t)=t-1,F(t)= g(t)-f(t)=t-lnt-1-(t-1)=-lnt<0,
∴F(t)没有零点;
当t时,f(t)=t-2,F(t)= g(t)-f(t)=t-lnt-1-(t-2)=1-lnt,
F(2)=1-ln2>0,
F(2.8)=1-ln2.8<0,∴F(t)在上存在唯一的零点,∵(t)= - <0,
∴F(t)在上单调递减,F(t)在上恒小于零,不存在零点
∴F(t)在上有且只有一个零点;
当t时,f(t)=t-3, F(t)= g(t)-f(t)=t-lnt-1-(t-3)=2-lnt,
∵3≤t<4, ln3≤lnt
∵g(4)-1=4-ln4-1-1=2-ln4>0,∴g(4)>1;∵t>4时,函数 g(t)单调递增,
∴当t≥4时,g(t)≥g(4)>1,函数 g(t)的图像与函数f(t)的图像不再有公共点;
综上所述方程x +1实数解的个数为3.
4.求函数 的值域。
解析:
方法一:令=k,得方程{x}=kx(x≠0)有实数解, 即函数y={x}与函数y=kx(x≠0)的图像有公共点,如图所示,得到两个图像有公共点时的三种不同情况:
K<0时,两个图像总有公共点;k=1时两个图像有完全重合的部分,有无数个公共点;0≤k<时两个图像有公共点;
而当k>1或≤k<1时,两个图像显然没有公共点。
综上所述k的取值范围为{k|k=1或k<},即函数 的值域为
{1}U(-)。
方法二:
= =1-
当x<0时,{x}≥0,∴≤0; x时,=- ,
==1- =1+,当x时,-;
x时,==1,
x时,=1- =1- <1- = ,
x时,=1- =1- <1- = ,
……
x时,=1- =1- <1- = >0,
……
综上所述函数 的值域为{1}U(-)。
方法三
= =1-
令1- =m,得方程[x]=(1-m)x(x≠0)有实数解,即函数y=[x]与函数y=(1-m)x(x≠0)的图像有公共点,如图所示,得到两个图像有公共点时的三种不同情况:
当1-m=0或1-m≥1或 <1-m<1时两个图像有公共点,
即m=1或0≤m<时两个图像有公共点;
综上所述函数 的值域为{1}U(-)。
5.已知a<0,若方程{x}+{2x}- =a(x-)(x≥0)有且只有2个实数根,求实数a的取值范围。
解析:由题意得,函数y={x}+{2x}与函数y=a(x-)+(x≥0)的图像有且只有2个公共点,如图所示,
得-1
6.若关于x的方程2{x}=2+logax(a>0,a≠1)有且只有2个实数根,求实数a的取值范围。
解析:由题意得函数y=2{x}(x>0)与函数y=2+logax(x>0)的图像有且只有2个公共点,如图所示,
得2+loga2≥0且2+loga3<0,解得;
即实数a的取值范围为(,]。
7.解方程[x]+[2x]=6.
解: x为不大于0的数时不适合原方程;∵[2x]≥2[x],
∴3[x]≤6,得[x]≤2,∴[x]=1或2;
当[x]=1时,1≤x<2,2≤2x<4,得[2x]=2或3,[x]+[2x]≠6;
当[x]=2时,由原方程得[2x]=4,∴4≤2x<5,令x=2+(0≤<1),则4≤2x=4+2<5, ∴0≤<, 即2≤<.
经验证2≤<是原方程的解,
∴原方程的解为2≤<。
8.求方程[5x+3]=4x+ 的所有解的和.
解:令t=5x+3,则x=,原方程化为[t]= + .
∴t-{t}= + ,即{t}=t+ ;
画出函数y={t}与y=t+的图像得方程{t}=t+有四个实数根,分别在(-4,-3),(-3,-2),(-2,-1),(-1,0)上;
当t(-4,-3)时,t-(-4)=t+ ,解得t=- , ∴x=- ;
当t(-3,-2)时,t-(-3)=t+ ,解得t=- , ∴x=- ;
当t(-2,-1)时,t-(-2)=t+ ,解得t=- , ∴x=- ;
当t(-1,0)时,t-(-1)=t+ ,解得t=- , ∴x=- ;
∴原方程的所有解的和为- - - - =-4.
9.已知函数,求函数的值域。
解析: = = =5 - +
= - ;
由0<<5得<<,
即函数的值域为{0,1,2,3,4,5 }.
10.数列{}中,= ,=-+1,
求[ + +……+]
解析:由=-+1得
-1=(-1),由=>1 ,得>1;
∴ = = - ,
= - ,
= - ,
= - ,
…………
= - ,
∴ = - ( + +……+),
得 + +……+= - < = 2,
+ +……+> + = + = >1,
∴[ + +……+]=1.
11.数列{}满足=0,=,数列{}满足{}=
(1)求,,的值,并证明数列{}是等比数列.
(2)设,求数列{}的前2n项和。
解析:(1)=2=0,=+2=2,=2=4,=+2=6,
∴=+2=2,=+2=4,=+2=8;
=+2=+4=2+4=2(+2)=2,
∴数列{}是公比为2的等比数列.
由(1)得=,=[],
n为偶数时,
=,
=[]=[]
=[ ]
=;
∴3==-1
∴=;
n为奇数时,=.
=[]=[]
=-+-+……+-]
=-+-+……+-1,
∴3(+1)=-+-+……+3,
3(+1)-1=-+-+……+3-==,
∴=-1= ;
即= 。
数列{}的前2n项和
=+++……+=(++……+)+(++……+)
=(++……+)+(++……+)
= += 。
=;
求:[]
解析:由=(k;
得= ==
==
=+ ]
=+ ]
=+ )。
当n为偶数时
=
+ - - + + +……++ )
=+ )= ;
[]
=[]=[]=[1+]=1;
当n为奇数时
=
+ - - + + +……- - )
=- )=0;
[]=0;
综上所述[]的值为0,或1。
同课章节目录
