推理与证明(归纳推理)
图片预览









文档简介
课件33张PPT。合情推理
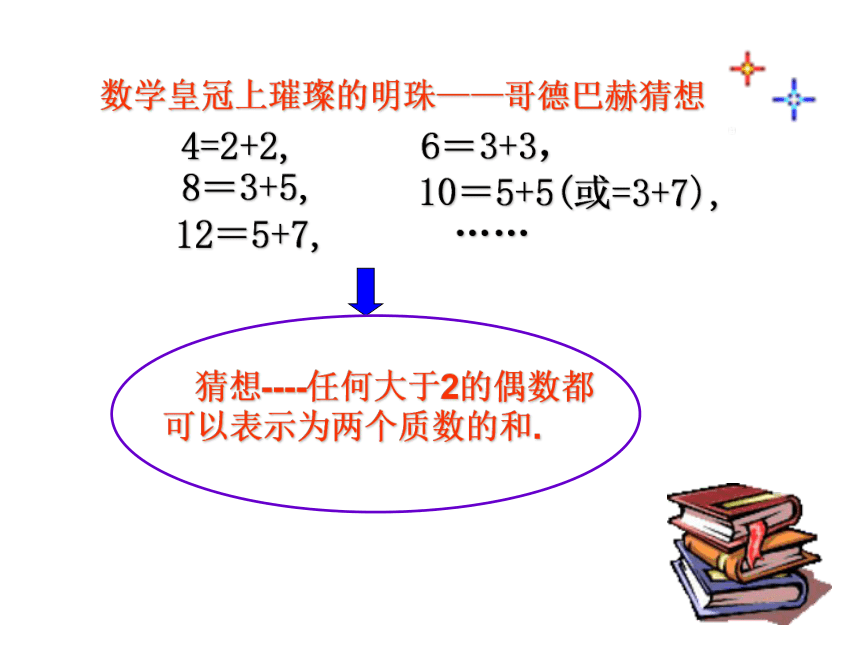
——归纳推理4=2+2,数学皇冠上璀璨的明珠——哥德巴赫猜想 猜想----任何大于2的偶数都可以表示为两个质数的和.6=3+3,8=3+5,10=5+5(或=3+7), 12=5+7,……推理:从一个或几个已知命题得出另一个新命题的思维过程称为推理。推理前提结论下面我们来考察几个推理实例。案例1:蛇是用肺呼吸的,鳄鱼是用肺呼吸的,海龟是用肺呼吸的,蜥蜴是用肺呼吸的。蛇、鳄鱼、海龟、蜥蜴都是爬行动物。由此猜想:案例2:三角形的内角和是180度,凸四边形的内角和是360度,凸五边形的内角和是540度,……由此猜想:所有的爬行动物都是用肺呼吸的。凸n边形的内角和是 (n-2) ×1800 。案例3:由此猜想:这些推理有什么共同的特点?从 中推演出
的推理,通常称为归纳推理.个别事实一般性的结论归纳推理 由某类事物的 具有某些特征,
推出该类事物的 都具有这些特征
的推理。部分对象全部对象
归纳推理的一般模式:S1具有P,S2具有P,……Sn具有P,(S1,S2,…,Sn是A类事物的对象)所以A类事物具有P。你能再举出一些归纳推理的实例吗?下列推理是归纳推理吗?为什么?
1、金受热后体积膨胀,
银受热后体积膨胀,
铜受热后体积膨胀,
铁受热后体积膨胀,
金、银、铜、铁都是金属。
所以,所有的金属受热后都体积膨胀。2、当n=0时,n2-n+11=11;
当n=1时,n2-n+11=11;
当n=2时,n2-n+11=13;
当n=3时,n2-n+11=17;
当n=4时,n2-n+11=23;
当n=5时,n2-n+11=31;
11,11,13,17,23,31都是质数.所以,对于所有的自然数n,n2-n+11的值都是质数.归纳推理得到的结论不一定正确! 4、长方形的对角线的平方等于长与 宽的平方和.
所以,长方体的对角线的平方等于长、宽、高的平方和. 3、所有的金属都能导电,
铁是金属,
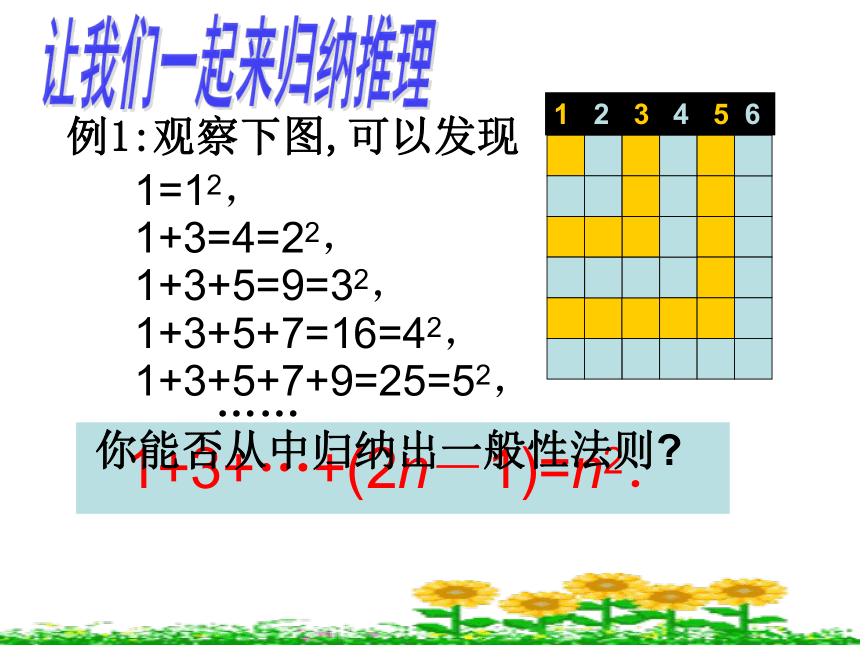
所以,铁能导电。 例1:观察下图,可以发现1+3+…+(2n-1)=n2.让我们一起来归纳推理1+3=4=22,1=12,1+3+5=9=32,1+3+5+7=16=42,1+3+5+7+9=25=52,……1 2 3 4 5 6 你能否从中归纳出一般性法则?例2.已知数列{ }的第一项 =1,
且 ( =1,2,3,···),
请先计算前四项
归纳出这个数列的通项公式为________.拓展延伸:
这样解严谨吗?
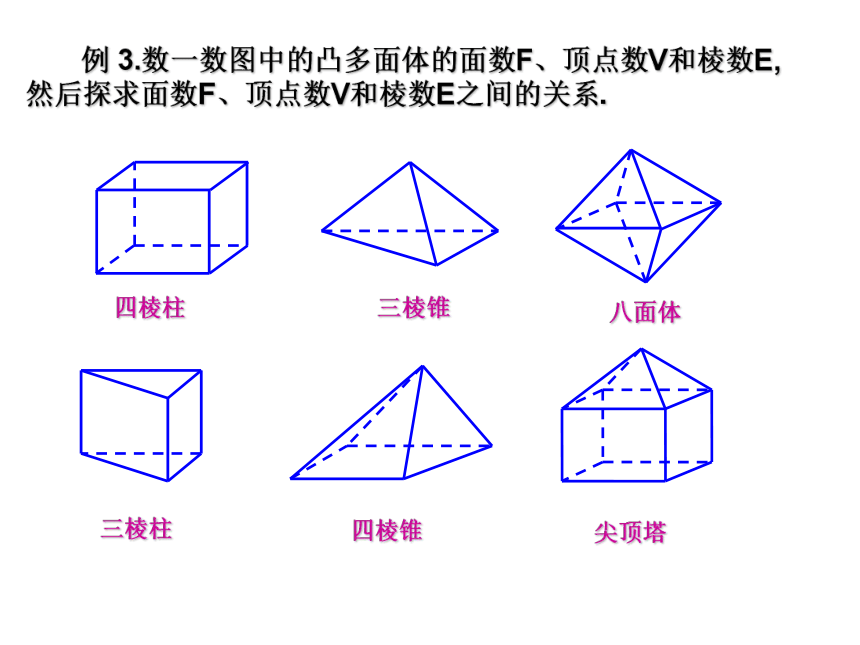
改为解答题,归纳的结论对你的解题思路有启发吗?归纳推理不但能猜测和发现结论,还能探索和提供解题思路。 例 3.数一数图中的凸多面体的面数F、顶点数V和棱数E,然后探求面数F、顶点数V和棱数E之间的关系.四棱柱三棱锥八面体三棱柱四棱锥尖顶塔四棱柱6812四棱柱6812644三棱锥四棱柱6812644三棱锥1286八面体四棱柱6812644三棱锥1286八面体695三棱柱四棱柱6812644三棱锥1286八面体695三棱柱558四棱锥四棱柱6812644三棱锥1286八面体695三棱柱558四棱锥9169尖顶塔695955816968126441286猜想凸多面体的面数F、顶点数V和棱数E之间的关系式为:F+V-E=2欧拉公式归纳推理得到的结论不一定可靠吆!阅读欣赏皇冠明珠:歌德巴赫猜想自然科学的皇后是数学,
数学的皇冠是数论,
歌德巴赫猜想是皇冠上的明珠 四色猜想的提出来自英国。1852年,毕业于伦敦大学的弗南西
斯·格思里来到一家科研单位搞地图着色工作时,发现了一种有
趣的现象:“看来,每幅地图都可以用四种颜色着色,使得有共
同边界的国家着上不同的颜色。”这个结论能不能从数学上加以
严格证明呢?他和在大学读书的弟弟格里斯决心试一试。兄弟二
人为证明这一问题而使用的稿纸已经堆了一大叠,可是研究工作
没有进展。
美国数学家富兰克林于1939年证明了22国以下的地图都可以
用四色着色。1950年,有人从22国推进到35国。1960年,有人又
证明了39国以下的地图可以只用四种颜色着色;随后又推进到了
50国。看来这种推进仍然十分缓慢。电子计算机问世以后,由于
演算速度迅速提高,加之人机对话的出现,大大加快了对四色猜
想证明的进程。1976年,美国数学家阿佩尔与哈肯在美国伊利诺
斯大学的两台不同的电子计算机上,用了1200个小时,作了100亿
判断,终于完成了四色定理的证明。四色猜想的计算机证明,轰
动了世界。它不仅解决了一个历时100多年的难题,而且有可能成
为数学史上一系列新思维的起点。不过也有不少数学家并不满足于
计算机取得的成就,他们还在寻找一种简捷明快的书面证明方法。
成语“一叶知秋” 意思是从一片树叶的凋落,知道秋
天将要来到.比喻由细微的迹象看出整体
形势的变化,由个别推知一般.谚语“瑞雪兆丰年”物理学中的波义耳-马略特定律化学中的门捷列夫元素周期表天文学中开普勒行星运动定律善于观察勤于思考敢于猜想的人常常会迸发出创造的灵感火花635课堂练习: 练习2:(梵塔传说)传说在古老的印度有一座神庙,神庙中有三根针和套在一根针上的64个圆环.古印度的天神指示他的僧侣们按下列规则,把圆环从一根针上全部移到另一根针上,第三根针起“过渡”的作用.
1.每次只能移动1个圆环;
2.较大的圆环不能放在较小的圆环上面.
如果有一天,僧侣们将这64个圆环全部移到另一根针上,那么世界末日就来临了.
请你试着推测:把 个圆环从1号针移到3号针,最少需要移动多少次?123 1883年法国的数学家 Edouard Lucas
提出的河内塔问题(Tower of Hanoi)。 123第1个圆环从1到3.设 为把 个圆环从1号针移到3号针的最少次数,则 =1时, =1 =2时,123第1个圆环从1到3.前1个圆环从1到2;
第2个圆环从1到3;
第1个圆环从2到3.设 为把 个圆环从1号针移到3号针的最少次数,则 =1 =1时, =3 =2时, =3 =1时, =1 =3时,123第1个圆环从1到3.前1个圆环从1到2;
第2个圆环从1到3;
前1个圆环从2到3.前2个圆环从1到2;
第3个圆环从1到3;
前2个圆环从2到3.设 为把 个圆环从1号针移到3号针的最少次数,则 =7猜想 an=2n -1设an为把n个圆环从一根针移到另一根针的最少次数,则课堂小结:这节课你有什么收获?学到了哪些知识?
2、归纳推理的特点、作用;1、推理、归纳推理的定义;注意归纳推理的结论不一定成立
——归纳推理4=2+2,数学皇冠上璀璨的明珠——哥德巴赫猜想 猜想----任何大于2的偶数都可以表示为两个质数的和.6=3+3,8=3+5,10=5+5(或=3+7), 12=5+7,……推理:从一个或几个已知命题得出另一个新命题的思维过程称为推理。推理前提结论下面我们来考察几个推理实例。案例1:蛇是用肺呼吸的,鳄鱼是用肺呼吸的,海龟是用肺呼吸的,蜥蜴是用肺呼吸的。蛇、鳄鱼、海龟、蜥蜴都是爬行动物。由此猜想:案例2:三角形的内角和是180度,凸四边形的内角和是360度,凸五边形的内角和是540度,……由此猜想:所有的爬行动物都是用肺呼吸的。凸n边形的内角和是 (n-2) ×1800 。案例3:由此猜想:这些推理有什么共同的特点?从 中推演出
的推理,通常称为归纳推理.个别事实一般性的结论归纳推理 由某类事物的 具有某些特征,
推出该类事物的 都具有这些特征
的推理。部分对象全部对象
归纳推理的一般模式:S1具有P,S2具有P,……Sn具有P,(S1,S2,…,Sn是A类事物的对象)所以A类事物具有P。你能再举出一些归纳推理的实例吗?下列推理是归纳推理吗?为什么?
1、金受热后体积膨胀,
银受热后体积膨胀,
铜受热后体积膨胀,
铁受热后体积膨胀,
金、银、铜、铁都是金属。
所以,所有的金属受热后都体积膨胀。2、当n=0时,n2-n+11=11;
当n=1时,n2-n+11=11;
当n=2时,n2-n+11=13;
当n=3时,n2-n+11=17;
当n=4时,n2-n+11=23;
当n=5时,n2-n+11=31;
11,11,13,17,23,31都是质数.所以,对于所有的自然数n,n2-n+11的值都是质数.归纳推理得到的结论不一定正确! 4、长方形的对角线的平方等于长与 宽的平方和.
所以,长方体的对角线的平方等于长、宽、高的平方和. 3、所有的金属都能导电,
铁是金属,
所以,铁能导电。 例1:观察下图,可以发现1+3+…+(2n-1)=n2.让我们一起来归纳推理1+3=4=22,1=12,1+3+5=9=32,1+3+5+7=16=42,1+3+5+7+9=25=52,……1 2 3 4 5 6 你能否从中归纳出一般性法则?例2.已知数列{ }的第一项 =1,
且 ( =1,2,3,···),
请先计算前四项
归纳出这个数列的通项公式为________.拓展延伸:
这样解严谨吗?
改为解答题,归纳的结论对你的解题思路有启发吗?归纳推理不但能猜测和发现结论,还能探索和提供解题思路。 例 3.数一数图中的凸多面体的面数F、顶点数V和棱数E,然后探求面数F、顶点数V和棱数E之间的关系.四棱柱三棱锥八面体三棱柱四棱锥尖顶塔四棱柱6812四棱柱6812644三棱锥四棱柱6812644三棱锥1286八面体四棱柱6812644三棱锥1286八面体695三棱柱四棱柱6812644三棱锥1286八面体695三棱柱558四棱锥四棱柱6812644三棱锥1286八面体695三棱柱558四棱锥9169尖顶塔695955816968126441286猜想凸多面体的面数F、顶点数V和棱数E之间的关系式为:F+V-E=2欧拉公式归纳推理得到的结论不一定可靠吆!阅读欣赏皇冠明珠:歌德巴赫猜想自然科学的皇后是数学,
数学的皇冠是数论,
歌德巴赫猜想是皇冠上的明珠 四色猜想的提出来自英国。1852年,毕业于伦敦大学的弗南西
斯·格思里来到一家科研单位搞地图着色工作时,发现了一种有
趣的现象:“看来,每幅地图都可以用四种颜色着色,使得有共
同边界的国家着上不同的颜色。”这个结论能不能从数学上加以
严格证明呢?他和在大学读书的弟弟格里斯决心试一试。兄弟二
人为证明这一问题而使用的稿纸已经堆了一大叠,可是研究工作
没有进展。
美国数学家富兰克林于1939年证明了22国以下的地图都可以
用四色着色。1950年,有人从22国推进到35国。1960年,有人又
证明了39国以下的地图可以只用四种颜色着色;随后又推进到了
50国。看来这种推进仍然十分缓慢。电子计算机问世以后,由于
演算速度迅速提高,加之人机对话的出现,大大加快了对四色猜
想证明的进程。1976年,美国数学家阿佩尔与哈肯在美国伊利诺
斯大学的两台不同的电子计算机上,用了1200个小时,作了100亿
判断,终于完成了四色定理的证明。四色猜想的计算机证明,轰
动了世界。它不仅解决了一个历时100多年的难题,而且有可能成
为数学史上一系列新思维的起点。不过也有不少数学家并不满足于
计算机取得的成就,他们还在寻找一种简捷明快的书面证明方法。
成语“一叶知秋” 意思是从一片树叶的凋落,知道秋
天将要来到.比喻由细微的迹象看出整体
形势的变化,由个别推知一般.谚语“瑞雪兆丰年”物理学中的波义耳-马略特定律化学中的门捷列夫元素周期表天文学中开普勒行星运动定律善于观察勤于思考敢于猜想的人常常会迸发出创造的灵感火花635课堂练习: 练习2:(梵塔传说)传说在古老的印度有一座神庙,神庙中有三根针和套在一根针上的64个圆环.古印度的天神指示他的僧侣们按下列规则,把圆环从一根针上全部移到另一根针上,第三根针起“过渡”的作用.
1.每次只能移动1个圆环;
2.较大的圆环不能放在较小的圆环上面.
如果有一天,僧侣们将这64个圆环全部移到另一根针上,那么世界末日就来临了.
请你试着推测:把 个圆环从1号针移到3号针,最少需要移动多少次?123 1883年法国的数学家 Edouard Lucas
提出的河内塔问题(Tower of Hanoi)。 123第1个圆环从1到3.设 为把 个圆环从1号针移到3号针的最少次数,则 =1时, =1 =2时,123第1个圆环从1到3.前1个圆环从1到2;
第2个圆环从1到3;
第1个圆环从2到3.设 为把 个圆环从1号针移到3号针的最少次数,则 =1 =1时, =3 =2时, =3 =1时, =1 =3时,123第1个圆环从1到3.前1个圆环从1到2;
第2个圆环从1到3;
前1个圆环从2到3.前2个圆环从1到2;
第3个圆环从1到3;
前2个圆环从2到3.设 为把 个圆环从1号针移到3号针的最少次数,则 =7猜想 an=2n -1设an为把n个圆环从一根针移到另一根针的最少次数,则课堂小结:这节课你有什么收获?学到了哪些知识?
2、归纳推理的特点、作用;1、推理、归纳推理的定义;注意归纳推理的结论不一定成立
