1.1.1 集合的含义与表示 课件2(第2课时)
文档属性
| 名称 | 1.1.1 集合的含义与表示 课件2(第2课时) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-08-01 23:15:47 | ||
图片预览




文档简介
课件11张PPT。学习目标:
掌握集合的表示方法—列举法、描述法、图示法. (重点)
能够运用集合的各种表示方法表示一些简单集合。(难点)第2课时 集合的表示
用列举法表示下列集合
(1)由小于8的所有素数组成的集合
(2)一次函数y=x+3与y=-2x+6的图象的交点组成的集合
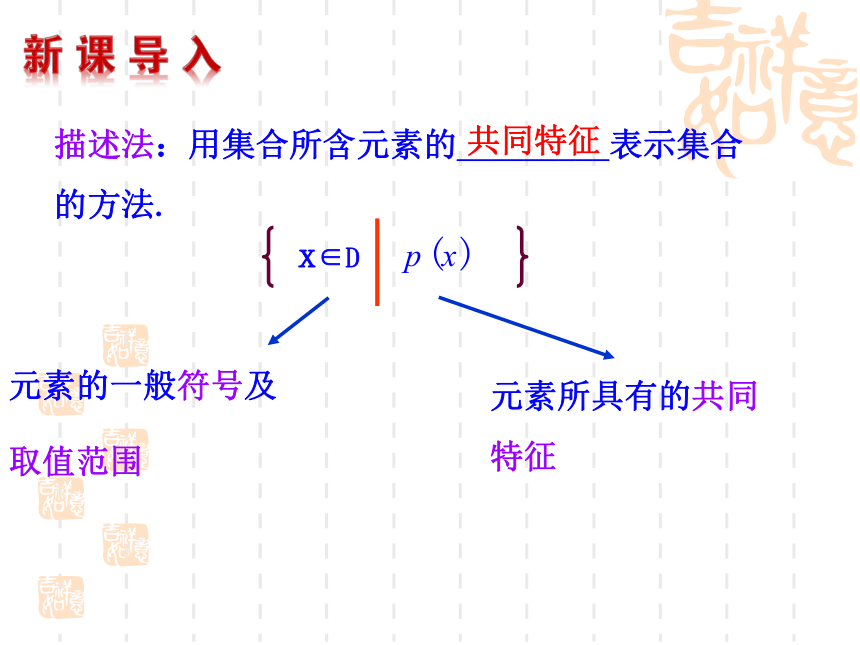
(3)不等式x-3<7的解集思考:是否所有集合都能用列举法来表示?否,集合中的元素个数是有限的,即有限集可以用.为无限集,无法用列举法表示.自主探究:描述法:用集合所含元素的_________表示集合
的方法.元素的一般符号及取值范围元素所具有的共同特征共同特征【想一想】1. a与{a}的含义是否相同?2. 集合{y|y=x2,x∈R}与集合{x|y=x2, x∈R}相同吗?不同,前者为元素,后者为集合.不同,前者是函数的所有函数值组成的集合;
后者是函数的所有自变量组成的集合.例2 试分别用列举法和描述法表示下列集合.(1)方程x2-2=0的所有实数根组成的集合.
(2)由大于10小于20的所有整数组成的集合. 方程x2-2=0有两个实数根为 ,因此,用列举法
表示为A={ }.解:(1)设方程x2-2=0的实数根为x,并且满足条件
x2-2=0,因此,用描述法表示为A={x∈R|x2-2=0}.大于10小于20的整数有11,12,13,14,15,16,17, 18,19,因此,用列举法表示为B={x∈Z∣10(1)不等式4x-5<3的解集
(2)二次函数y=x2-4的函数值组成的集合
(3)反比例函数 的自变量的值组成的集合
(4)不等式3x≥4-2x的解集{ x∈R|x≠0}{y∈R|y≥-4}{ x∈R | }{ x∈R|x<2}【变式练习】1.用列举法表示集合{x|x2-2x+1=0}为( )
A.{1,1} B.{1}
C.{x=0} D.{x2-2x+1=0}
【解析】集合{x|x2-2x+1=0}是方程x2-2x+1=0的解集,而方程有两个相等的实根1,故可表示为{1}.B2.集合{(x,y)|y=2x-1}表示( )
A.方程y=2x-1
B.点(x,y)
C.平面直角坐标系中所有的点组成的集合
D.函数y=2x-1的图象上的所有点组成的集合
【解析】该集合是一个点集,表示函数y=2x-1图象上的所有点组成的集合.D3.用适当的方法表示下列给定的集合.
(1)比4大2的数.
(2)所有奇数组成的集合.
(3)大于1且小于6的整数.
掌握集合的表示方法—列举法、描述法、图示法. (重点)
能够运用集合的各种表示方法表示一些简单集合。(难点)第2课时 集合的表示
用列举法表示下列集合
(1)由小于8的所有素数组成的集合
(2)一次函数y=x+3与y=-2x+6的图象的交点组成的集合
(3)不等式x-3<7的解集思考:是否所有集合都能用列举法来表示?否,集合中的元素个数是有限的,即有限集可以用.为无限集,无法用列举法表示.自主探究:描述法:用集合所含元素的_________表示集合
的方法.元素的一般符号及取值范围元素所具有的共同特征共同特征【想一想】1. a与{a}的含义是否相同?2. 集合{y|y=x2,x∈R}与集合{x|y=x2, x∈R}相同吗?不同,前者为元素,后者为集合.不同,前者是函数的所有函数值组成的集合;
后者是函数的所有自变量组成的集合.例2 试分别用列举法和描述法表示下列集合.(1)方程x2-2=0的所有实数根组成的集合.
(2)由大于10小于20的所有整数组成的集合. 方程x2-2=0有两个实数根为 ,因此,用列举法
表示为A={ }.解:(1)设方程x2-2=0的实数根为x,并且满足条件
x2-2=0,因此,用描述法表示为A={x∈R|x2-2=0}.大于10小于20的整数有11,12,13,14,15,16,17, 18,19,因此,用列举法表示为B={x∈Z∣10
(2)二次函数y=x2-4的函数值组成的集合
(3)反比例函数 的自变量的值组成的集合
(4)不等式3x≥4-2x的解集{ x∈R|x≠0}{y∈R|y≥-4}{ x∈R | }{ x∈R|x<2}【变式练习】1.用列举法表示集合{x|x2-2x+1=0}为( )
A.{1,1} B.{1}
C.{x=0} D.{x2-2x+1=0}
【解析】集合{x|x2-2x+1=0}是方程x2-2x+1=0的解集,而方程有两个相等的实根1,故可表示为{1}.B2.集合{(x,y)|y=2x-1}表示( )
A.方程y=2x-1
B.点(x,y)
C.平面直角坐标系中所有的点组成的集合
D.函数y=2x-1的图象上的所有点组成的集合
【解析】该集合是一个点集,表示函数y=2x-1图象上的所有点组成的集合.D3.用适当的方法表示下列给定的集合.
(1)比4大2的数.
(2)所有奇数组成的集合.
(3)大于1且小于6的整数.
