1.1.1 集合的含义与表示 学案1(含答案)
文档属性
| 名称 | 1.1.1 集合的含义与表示 学案1(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 75.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-08-01 00:00:00 | ||
图片预览


文档简介
1.1.1
集合的含义与表示
班级:__________姓名:__________设计人__________日期__________
课前预习
·
预习案
【温馨寄语】
如果明天是一幢摩天大厦,今天就是决定那大厦寿命的基石。同学们,让我们珍惜今天这一分一秒,把这大厦的基石打得无比坚实。
【使用说明】
(1)独立研读教材,作好标记和勾画,标注关键词.
(2)根据预习指导,再次研读教材,自主探究导学案问题,思考并完成课前预习部分.
【学习目标】
(1)了解集合的含义,理解集合中元素的三个特性,并能利用集合的三个特性解题.
(2)掌握元素与集合之间的关系,并能用符号表示
(3)掌握两种表示集合的方法——列举法和描述法.
(4)能够运用集合的列举法、描述法表示一些简单的集合
【学习重点】
集合中元素的确定性和互异性;表示方法恰当的选择
【高考要求】
1.集合的含义与表示是高考的考查热点;
2.常考题型为新定义的一个集合,求集合中的元素个数,常以选择题的形式出现,分值为4-5分.
【预备知识】
①什么是素数
②在初中,圆是如何定义的?
③实数是如何分布的?
【自主学习】
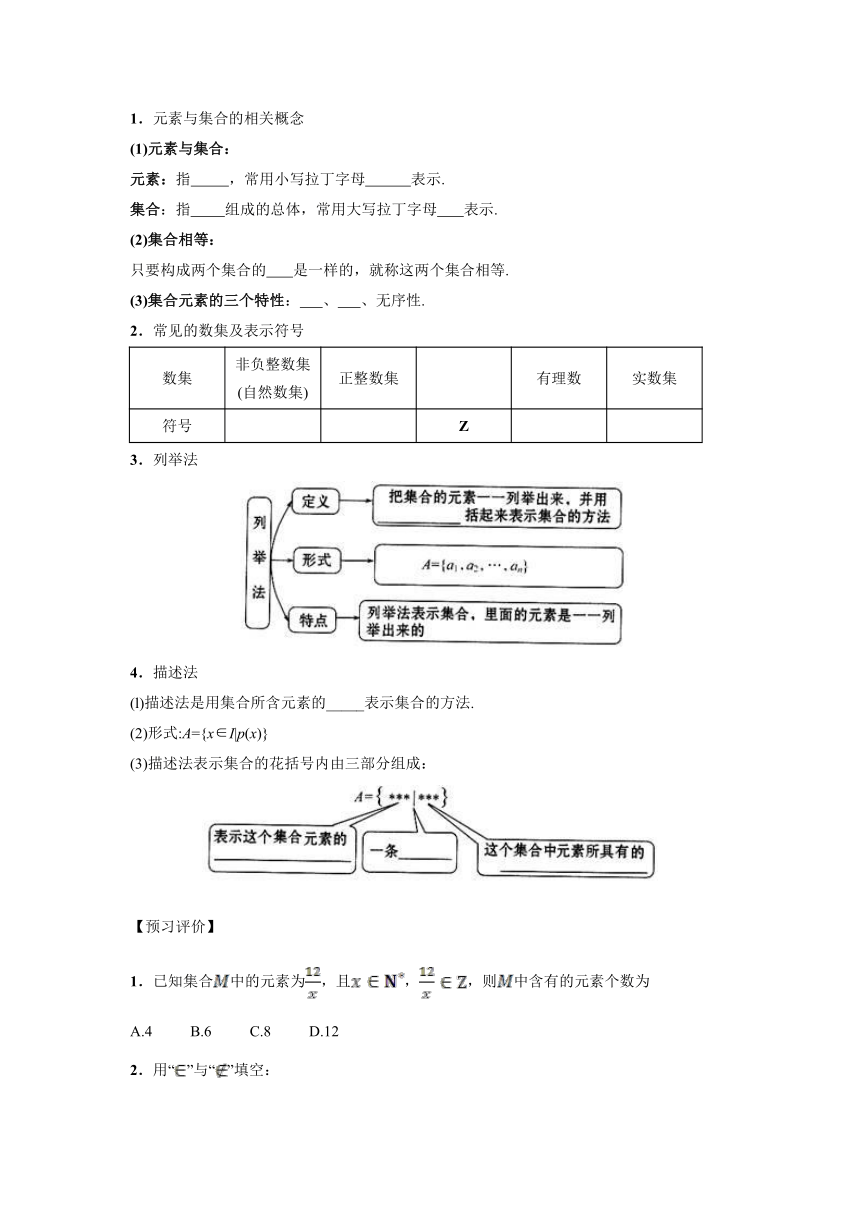
1.元素与集合的相关概念
(1)元素与集合:
元素:指
,常用小写拉丁字母
表示.
集合:指
组成的总体,常用大写拉丁字母
表示.
(2)集合相等:
只要构成两个集合的
是一样的,就称这两个集合相等.
(3)集合元素的三个特性: 、 、无序性.
2.常见的数集及表示符号
数集
非负整数集(自然数集)
正整数集
有理数
实数集
符号
Z
3.列举法
4.描述法
(l)描述法是用集合所含元素的_____表示集合的方法.
(2)形式:A={x∈I|p(x)}
(3)描述法表示集合的花括号内由三部分组成:
【预习评价】
1.已知集合中的元素为,且,,则中含有的元素个数为
A.4
B.6
C.8
D.12
2.用“”与“”填空:
_____
;
________
;
2
_________
.
3.某书架上有5种不同品种的书各3本,那么由这个书架上的书组成的集合中含有____个元素.
4.已知集合,,则实数的值为
A.4
B.3
C.2
D.1
5.用描述法表示大于3且不大于8的实数的集合为______________.
6.若集合与集合相等,则=____________,=______________.
高效课堂
·
探究案
【合作探究】
1.元素与集合的含义
在初中数学中,我们已经接触过与集合有关的问题,并且也用集合描述过一些概念,请根据有关提示完成下面的填空,初步体会集合的含义.
(1)解集:在学习一元一次不等式时,提到________的解集.
(2)圆的定义:用集合描述圆的定义是_________等于定长的点的集合.
2.元素与集合的关系
由山东的十七地市构成的集合记作,试用“”或“”完成下列填空.
张家口____________,济南____________,
德州_____________,连云港___________.
3.根据列举法的定义,思考下列问题:
(1)我国的五岳能组成集合吗?若能,试用列举法表示出来.
(2)你能用列举法表示“不大于200的正偶数组成的集合”吗?
(3)在(l),(2)的基础上,思考在什么情况下适宜用列举法表示集合?
4.描述法表示集合
请观察下列给出的两个问题,根据描述法的定义,探究以下问题:
①不等式的解集;②绝对值小于2的实数组成的集合.
(1)这两个集合能否用列举法表示?
(2)如何用数学式子描述上述两个集合的元素特征?用集合怎样表示?
【教师点拨】
1.对元素与集合含义的两点说明
(1)元素是研究对象的统称,可以是任何研究对象,如数、点、解析式等.
(2)日常生活中所说的“集合”是指将分散的人或事物聚集到一起;数学中的“集合”是指研究对象构成的总体.
2.集合中元素的三个特性的意义
3.列举法表示集合时的四个关注点
(1)元素与元素之间必须用“,”隔开.
(2)集合中的元素必须是明确的.
(3)集合中的元素不能重复.
(4)集合中的元素可以是任何事物,
4.对描述法表示集合的两点说明
(1)描述法的构成:描述法一般由花括号、元素的一般形式、竖线和元素的共同性质四部分构成.其中最关键的是元素的共同性质,它是集合中元素的共性,是该集合的核心.
(2)描述法的一般格式:,它表示由满足的所有元素组成的集合,其中是所有元素的代表,表示元素所具有的共性.
【交流展示】
1.以下元素的全体不能组成集合的是
A.中国古代四大发明
B.地球上的小河流
C.方程的实数解
D.周长为10cm的三角形
2.下列所给关系正确的个数为
(l).
(2).
(3).
(4).
A.1
B.2
C.3
D.4
3.由数32
321中的数字组成的集合中含有________个元素.
4.用列举法表示方程的解集为________________.
5.设,则集合 中所有元素之积为___________________.
6.用描述法表示下列集合:
(1)集合可表示为_________________.
(2)集合可表示为______________.
【当堂检测】
1.下面各组对象能组成集合的有______________.
(1)某校2013年高一新生中的所有聪明的同学.
(2)不超过20的非负数.
(3)方程在实数范围内的解.
(4)直角坐标平面内第一象限的一些点.
(5)的近似值的全体.
2.已知集合由0,,三个元素组成,且,则实数=________.
3.已知集合,集合中的元素满足,,,则集合=_____________.
4.用描述法表示下列集合:
(1)被3除余1的正整数的集合.
(2)坐标平面内第一象限内的点的集合.
(3)大于4的所有偶数.
5.设集合,,若,求集合.
1.1.1
集合的含义与表示
详细答案
课前预习
·
预习案
【自主学习】
1.(1)研究对象 a,b,c,…元素
A,B,C…
(2)元素 (3)确定性 互异性
2.整数集 N N
或N+ Q R
3.花括号“{}”
4.(1)共同特征
(3)一般符号及取值(或变化)范围
竖线
共同特征
【预习评价】
1.B
2. ∈ ∈
3.5
4.B
5.{x|3<x≤8}
6.4 1
高效课堂
·
探究案
【合作探究】
1.(1)不等式 (2)到定点的距离
2. ∈ ∈
提示 根据元素与集合的关系,若是该集合中的元素,用“∈”,否则用“ ”.
3.(1)提示 能.用列举法表示为{泰山,华山,衡山,恒山,嵩山}.
(2)提示 能.用列举法表示为{2,4,6,8,…,200}.
(3)提示 ①集合中的元素较少,能够一一列举出来时,适合用列举法;②集合中的元素较多或无限多,但呈现一定的规律性时.也可以列举出几个元素作为代表,其他元素用省略号表示.
4.(1)提示 不能,因为两个集合里的元素都无法一一列举出来且不具有一定的规律.
(2)提示 ①x∈R且x<5.用集合表示为{x∈R|x<5},
②x∈R且|x|<2,用集合表示为{x∈R||x|<2}.
【交流展示】
1.B
2.B
3.3
4.{-1,1}
5.
6.(1){x|x=2n,n∈N
且n≤4}
(2){x|x=,n≤4且n∈N
}
【当堂检测】
1.(2)(3)
2.3
3.{4,10,25}
4.(1)根据被除数=商×除数+余数,可知此集合表示为{x|x=3n+1,n∈N}
(2)第一象限内的点的横、纵坐标均大于零,故此集合可表示为{(x,y)|x>0,y>0}.
(3)偶数可表示为2n,n∈Z,又因为大于4,故n≥3,从而用描述法表示此集合为{x|x=2n,n≥3,n∈Z}.
5.
集合的含义与表示
班级:__________姓名:__________设计人__________日期__________
课前预习
·
预习案
【温馨寄语】
如果明天是一幢摩天大厦,今天就是决定那大厦寿命的基石。同学们,让我们珍惜今天这一分一秒,把这大厦的基石打得无比坚实。
【使用说明】
(1)独立研读教材,作好标记和勾画,标注关键词.
(2)根据预习指导,再次研读教材,自主探究导学案问题,思考并完成课前预习部分.
【学习目标】
(1)了解集合的含义,理解集合中元素的三个特性,并能利用集合的三个特性解题.
(2)掌握元素与集合之间的关系,并能用符号表示
(3)掌握两种表示集合的方法——列举法和描述法.
(4)能够运用集合的列举法、描述法表示一些简单的集合
【学习重点】
集合中元素的确定性和互异性;表示方法恰当的选择
【高考要求】
1.集合的含义与表示是高考的考查热点;
2.常考题型为新定义的一个集合,求集合中的元素个数,常以选择题的形式出现,分值为4-5分.
【预备知识】
①什么是素数
②在初中,圆是如何定义的?
③实数是如何分布的?
【自主学习】
1.元素与集合的相关概念
(1)元素与集合:
元素:指
,常用小写拉丁字母
表示.
集合:指
组成的总体,常用大写拉丁字母
表示.
(2)集合相等:
只要构成两个集合的
是一样的,就称这两个集合相等.
(3)集合元素的三个特性: 、 、无序性.
2.常见的数集及表示符号
数集
非负整数集(自然数集)
正整数集
有理数
实数集
符号
Z
3.列举法
4.描述法
(l)描述法是用集合所含元素的_____表示集合的方法.
(2)形式:A={x∈I|p(x)}
(3)描述法表示集合的花括号内由三部分组成:
【预习评价】
1.已知集合中的元素为,且,,则中含有的元素个数为
A.4
B.6
C.8
D.12
2.用“”与“”填空:
_____
;
________
;
2
_________
.
3.某书架上有5种不同品种的书各3本,那么由这个书架上的书组成的集合中含有____个元素.
4.已知集合,,则实数的值为
A.4
B.3
C.2
D.1
5.用描述法表示大于3且不大于8的实数的集合为______________.
6.若集合与集合相等,则=____________,=______________.
高效课堂
·
探究案
【合作探究】
1.元素与集合的含义
在初中数学中,我们已经接触过与集合有关的问题,并且也用集合描述过一些概念,请根据有关提示完成下面的填空,初步体会集合的含义.
(1)解集:在学习一元一次不等式时,提到________的解集.
(2)圆的定义:用集合描述圆的定义是_________等于定长的点的集合.
2.元素与集合的关系
由山东的十七地市构成的集合记作,试用“”或“”完成下列填空.
张家口____________,济南____________,
德州_____________,连云港___________.
3.根据列举法的定义,思考下列问题:
(1)我国的五岳能组成集合吗?若能,试用列举法表示出来.
(2)你能用列举法表示“不大于200的正偶数组成的集合”吗?
(3)在(l),(2)的基础上,思考在什么情况下适宜用列举法表示集合?
4.描述法表示集合
请观察下列给出的两个问题,根据描述法的定义,探究以下问题:
①不等式的解集;②绝对值小于2的实数组成的集合.
(1)这两个集合能否用列举法表示?
(2)如何用数学式子描述上述两个集合的元素特征?用集合怎样表示?
【教师点拨】
1.对元素与集合含义的两点说明
(1)元素是研究对象的统称,可以是任何研究对象,如数、点、解析式等.
(2)日常生活中所说的“集合”是指将分散的人或事物聚集到一起;数学中的“集合”是指研究对象构成的总体.
2.集合中元素的三个特性的意义
3.列举法表示集合时的四个关注点
(1)元素与元素之间必须用“,”隔开.
(2)集合中的元素必须是明确的.
(3)集合中的元素不能重复.
(4)集合中的元素可以是任何事物,
4.对描述法表示集合的两点说明
(1)描述法的构成:描述法一般由花括号、元素的一般形式、竖线和元素的共同性质四部分构成.其中最关键的是元素的共同性质,它是集合中元素的共性,是该集合的核心.
(2)描述法的一般格式:,它表示由满足的所有元素组成的集合,其中是所有元素的代表,表示元素所具有的共性.
【交流展示】
1.以下元素的全体不能组成集合的是
A.中国古代四大发明
B.地球上的小河流
C.方程的实数解
D.周长为10cm的三角形
2.下列所给关系正确的个数为
(l).
(2).
(3).
(4).
A.1
B.2
C.3
D.4
3.由数32
321中的数字组成的集合中含有________个元素.
4.用列举法表示方程的解集为________________.
5.设,则集合 中所有元素之积为___________________.
6.用描述法表示下列集合:
(1)集合可表示为_________________.
(2)集合可表示为______________.
【当堂检测】
1.下面各组对象能组成集合的有______________.
(1)某校2013年高一新生中的所有聪明的同学.
(2)不超过20的非负数.
(3)方程在实数范围内的解.
(4)直角坐标平面内第一象限的一些点.
(5)的近似值的全体.
2.已知集合由0,,三个元素组成,且,则实数=________.
3.已知集合,集合中的元素满足,,,则集合=_____________.
4.用描述法表示下列集合:
(1)被3除余1的正整数的集合.
(2)坐标平面内第一象限内的点的集合.
(3)大于4的所有偶数.
5.设集合,,若,求集合.
1.1.1
集合的含义与表示
详细答案
课前预习
·
预习案
【自主学习】
1.(1)研究对象 a,b,c,…元素
A,B,C…
(2)元素 (3)确定性 互异性
2.整数集 N N
或N+ Q R
3.花括号“{}”
4.(1)共同特征
(3)一般符号及取值(或变化)范围
竖线
共同特征
【预习评价】
1.B
2. ∈ ∈
3.5
4.B
5.{x|3<x≤8}
6.4 1
高效课堂
·
探究案
【合作探究】
1.(1)不等式 (2)到定点的距离
2. ∈ ∈
提示 根据元素与集合的关系,若是该集合中的元素,用“∈”,否则用“ ”.
3.(1)提示 能.用列举法表示为{泰山,华山,衡山,恒山,嵩山}.
(2)提示 能.用列举法表示为{2,4,6,8,…,200}.
(3)提示 ①集合中的元素较少,能够一一列举出来时,适合用列举法;②集合中的元素较多或无限多,但呈现一定的规律性时.也可以列举出几个元素作为代表,其他元素用省略号表示.
4.(1)提示 不能,因为两个集合里的元素都无法一一列举出来且不具有一定的规律.
(2)提示 ①x∈R且x<5.用集合表示为{x∈R|x<5},
②x∈R且|x|<2,用集合表示为{x∈R||x|<2}.
【交流展示】
1.B
2.B
3.3
4.{-1,1}
5.
6.(1){x|x=2n,n∈N
且n≤4}
(2){x|x=,n≤4且n∈N
}
【当堂检测】
1.(2)(3)
2.3
3.{4,10,25}
4.(1)根据被除数=商×除数+余数,可知此集合表示为{x|x=3n+1,n∈N}
(2)第一象限内的点的横、纵坐标均大于零,故此集合可表示为{(x,y)|x>0,y>0}.
(3)偶数可表示为2n,n∈Z,又因为大于4,故n≥3,从而用描述法表示此集合为{x|x=2n,n≥3,n∈Z}.
5.
