新华东师大版七年级数学下册第九章平移的特征 课件(共17张PPT)
文档属性
| 名称 | 新华东师大版七年级数学下册第九章平移的特征 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-25 20:41:34 | ||
图片预览





文档简介
(共17张PPT)
华东师大版 七年级下册
第9章 轴对称、平移与旋转
9.2.2 平移的特征
在日常生活中,我们经常可以看到以下现象:
情境导入
1.探索平移的特征,准确理解平移的特征并会运用;(重点)
2.能根据所给条件作简单的平面图形平移后的图形.(难点)
学习目标
A
P
Q
B
C
A′
观察画平行线的过程,思考:
(1)平移后的新图形与原图形的什么发生了变化?
(2)找出图形中的三组对应线段,它们有什么关系?
(3)找出图形中的三组对应角,它们有什么关系?
C′
B′
进行新课
平移前后的两个图形有什么特征?
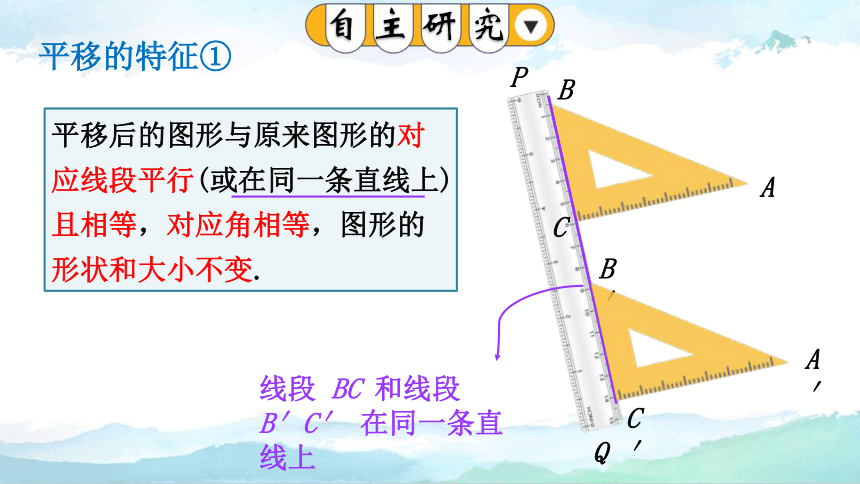
平移的特征①
平移后的图形与原来图形的对应线段平行(或在同一条直线上)且相等,对应角相等,图形的形状和大小不变.
线段 BC 和线段 B′C′ 在同一条直线上
A
P
Q
B
C
A′
C′
B′
自主研究
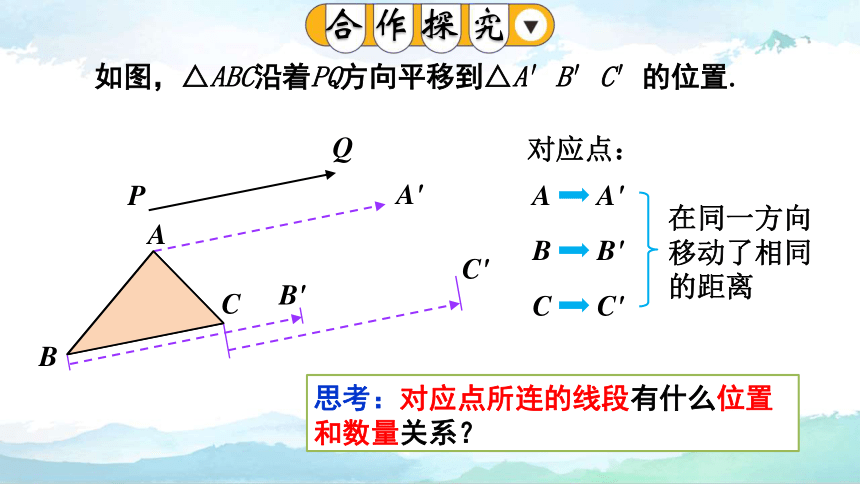
如图,△ABC沿着PQ方向平移到△A′B′C′的位置.
C'
A'
A
C
B
P
Q
思考:对应点所连的线段有什么位置和数量关系?
A
A'
B
B'
C
C'
在同一方向移动了相同的距离
对应点:
B'
合作探究
C'
A'
A
C
B'
B
P
Q
平移后对应点所连的线段平行(或在同一条直线上)且相等.
平移的特征②
线段 BB′ 和线段 CC′ 在同一条直线上
合作交流
例 如图,△ABC 经过平移到达△A′B′C′的位置. 指出平移的方向,并量出平移的距离.(精确到1 mm)
A
B
C
A′
B′
C′
解: (1)先找到对应点;
(2)连结两个对应点;
(3)由一个点平移到另一个点的移动方向,就是图形移动的方向.所以平移的方向就是点A到点A'的方向(或射线AA′的方向);
(4)平移的距离就是线段 AA′ 的长,经测量可知,约25mm.
注意:图形上的每个点都沿相同的方向平移相同的距离。
例题精讲
试一试
在如图的方格图中,作出将图中的△ABC向右平移4格后的△A′B′C′,然后再作出将△A′B′C′ 向上平移3格后的△A′′B′′C′′.
A
B
C
A′
B′
C′
A′′
B′′
C′′
△A′′B′′C′′是否可以看成是△ABC经过一次平移得到的?
如果是,你能说出平移的方向和距离吗?
多次平移相当于一次平移.
试一试
将下图中的△ABC沿PQ方向平移到△A′B′C′的位置,其平移的距离为线段PQ的长度.
C'
A'
A
C
B'
B
P
Q
平移作图
平移作图的一般步骤:
(1)定:确定平移前的图形、平移的方向和平移的距离;
(2)找:找出平移前的图形的关键点;
(3)移:沿一定方向、按一定距离平移各关键点,得到各关键点的对应点;
(4)连: 顺次连结所作的各个对应点,并标上相应的字母;
注意:平移作图找关键点是关键,关键点要找全。
练习:如图,经过平移,四边形ABCD的顶点A移动到点A′,作出平移后的四边形.
A
B
C
D
A′
D′
C′
B′
随堂演练
生活中一些图案可以看成由某一基本图案,在同一平面内沿着一定的方向平移若干次而成的.
1、本节课的学习,我们用到了哪些数学方法?
自主探究、观察猜想、合作交流、画图实践、演示验证、归纳总结
2、谈谈你的收获?
课堂交流
平移的特征
特征
平移作图
平移前后
对应线段
对应角
形状、大小
位置
平行(或共线)
相等
相等
对应点所连的线段
平行(或共线)
相等
定、找、移、连
课堂小结
不变:
改变:
数量:
位置:
数量:
位置:
数量:
基础题:课本136页习题第2、3题;
拔高题:课本136页习题第4、5题。
选做(拓展题):
1、如图,把△ABC 沿射线AD的方向平移2个单位长度至△DEF的位置,△ABC周长为10,则四边形ABFD的周长为
布置作业
2、利用如图所示的图形,通过平移在给出的方格图中设计图案。
平移可以创造美,希望大家带着数学之美,与奋发之力量,学以致用,知行合一!
华东师大版 七年级下册
第9章 轴对称、平移与旋转
9.2.2 平移的特征
在日常生活中,我们经常可以看到以下现象:
情境导入
1.探索平移的特征,准确理解平移的特征并会运用;(重点)
2.能根据所给条件作简单的平面图形平移后的图形.(难点)
学习目标
A
P
Q
B
C
A′
观察画平行线的过程,思考:
(1)平移后的新图形与原图形的什么发生了变化?
(2)找出图形中的三组对应线段,它们有什么关系?
(3)找出图形中的三组对应角,它们有什么关系?
C′
B′
进行新课
平移前后的两个图形有什么特征?
平移的特征①
平移后的图形与原来图形的对应线段平行(或在同一条直线上)且相等,对应角相等,图形的形状和大小不变.
线段 BC 和线段 B′C′ 在同一条直线上
A
P
Q
B
C
A′
C′
B′
自主研究
如图,△ABC沿着PQ方向平移到△A′B′C′的位置.
C'
A'
A
C
B
P
Q
思考:对应点所连的线段有什么位置和数量关系?
A
A'
B
B'
C
C'
在同一方向移动了相同的距离
对应点:
B'
合作探究
C'
A'
A
C
B'
B
P
Q
平移后对应点所连的线段平行(或在同一条直线上)且相等.
平移的特征②
线段 BB′ 和线段 CC′ 在同一条直线上
合作交流
例 如图,△ABC 经过平移到达△A′B′C′的位置. 指出平移的方向,并量出平移的距离.(精确到1 mm)
A
B
C
A′
B′
C′
解: (1)先找到对应点;
(2)连结两个对应点;
(3)由一个点平移到另一个点的移动方向,就是图形移动的方向.所以平移的方向就是点A到点A'的方向(或射线AA′的方向);
(4)平移的距离就是线段 AA′ 的长,经测量可知,约25mm.
注意:图形上的每个点都沿相同的方向平移相同的距离。
例题精讲
试一试
在如图的方格图中,作出将图中的△ABC向右平移4格后的△A′B′C′,然后再作出将△A′B′C′ 向上平移3格后的△A′′B′′C′′.
A
B
C
A′
B′
C′
A′′
B′′
C′′
△A′′B′′C′′是否可以看成是△ABC经过一次平移得到的?
如果是,你能说出平移的方向和距离吗?
多次平移相当于一次平移.
试一试
将下图中的△ABC沿PQ方向平移到△A′B′C′的位置,其平移的距离为线段PQ的长度.
C'
A'
A
C
B'
B
P
Q
平移作图
平移作图的一般步骤:
(1)定:确定平移前的图形、平移的方向和平移的距离;
(2)找:找出平移前的图形的关键点;
(3)移:沿一定方向、按一定距离平移各关键点,得到各关键点的对应点;
(4)连: 顺次连结所作的各个对应点,并标上相应的字母;
注意:平移作图找关键点是关键,关键点要找全。
练习:如图,经过平移,四边形ABCD的顶点A移动到点A′,作出平移后的四边形.
A
B
C
D
A′
D′
C′
B′
随堂演练
生活中一些图案可以看成由某一基本图案,在同一平面内沿着一定的方向平移若干次而成的.
1、本节课的学习,我们用到了哪些数学方法?
自主探究、观察猜想、合作交流、画图实践、演示验证、归纳总结
2、谈谈你的收获?
课堂交流
平移的特征
特征
平移作图
平移前后
对应线段
对应角
形状、大小
位置
平行(或共线)
相等
相等
对应点所连的线段
平行(或共线)
相等
定、找、移、连
课堂小结
不变:
改变:
数量:
位置:
数量:
位置:
数量:
基础题:课本136页习题第2、3题;
拔高题:课本136页习题第4、5题。
选做(拓展题):
1、如图,把△ABC 沿射线AD的方向平移2个单位长度至△DEF的位置,△ABC周长为10,则四边形ABFD的周长为
布置作业
2、利用如图所示的图形,通过平移在给出的方格图中设计图案。
平移可以创造美,希望大家带着数学之美,与奋发之力量,学以致用,知行合一!
