2025中考九年级数学圆专题复习隐圆问题 课件(共20张PPT)
文档属性
| 名称 | 2025中考九年级数学圆专题复习隐圆问题 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-25 20:44:17 | ||
图片预览





文档简介
(共20张PPT)
课前准备:
请准备好:导学案、练习本,双色笔, 更重要的是你的激情!
课前寄语:我的课堂,我做主!
相信自己,我是最棒的!
快乐学习,学习快乐!
中考数学第二轮复习
圆的专题复习:隐圆问题(一)
内乡复兴学校 符 青
考情分析
隐圆问题作为几何板块的重要内容,在河南中考试卷上频繁出现,2022年、2024年都出在第15题的位置。
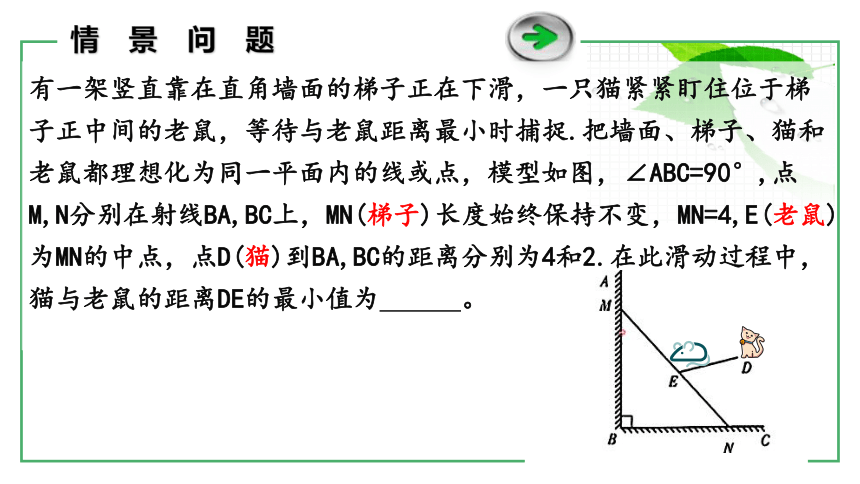
有一架竖直靠在直角墙面的梯子正在下滑,一只猫紧紧盯住位于梯子正中间的老鼠,等待与老鼠距离最小时捕捉.把墙面、梯子、猫和老鼠都理想化为同一平面内的线或点,模型如图,∠ABC=90°,点M,N分别在射线BA,BC上,MN(梯子)长度始终保持不变,MN=4,E(老鼠)为MN的中点,点D(猫)到BA,BC的距离分别为4和2.在此滑动过程中,猫与老鼠的距离DE的最小值为 。
情景问题
复习目标
1.会根据已知条件,确定隐圆模型,并画出隐圆
2.利用隐圆,能解决求角度、线段长及最值等数学问题
3.体会模型,分类讨论等基本数学思想方法
知识储备
1、圆的定义
2、圆周角定理
3、直角三角形的性质 (请同学们大声读背导学案上的内容)
4、点圆最值问题
5、线圆最值问题
九下教材内容
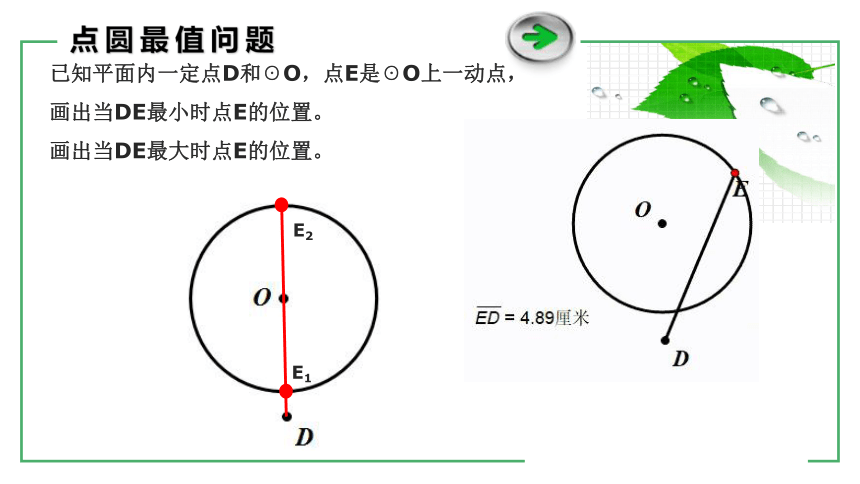
点圆最值问题
已知平面内一定点D和☉O,点E是☉O上一动点,画出当DE最小时点E的位置。
画出当DE最大时点E的位置。
E1
E2
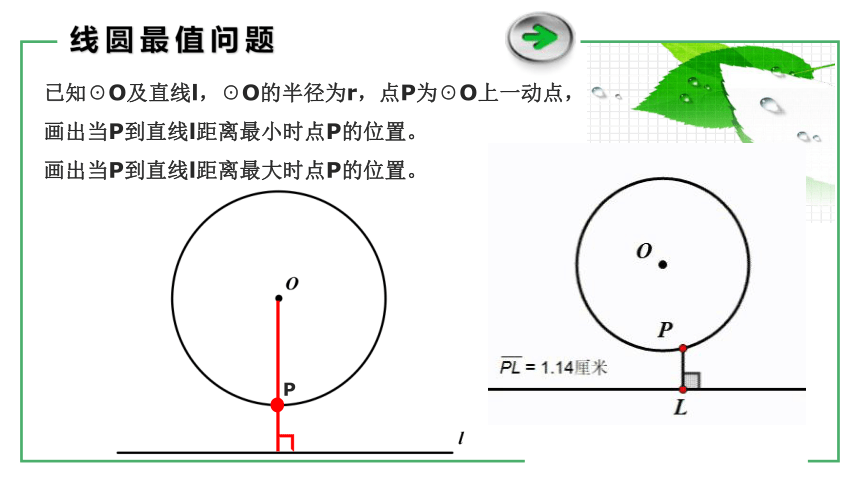
线圆最值问题
已知☉O及直线l,☉O的半径为r,点P为☉O上一动点,
画出当P到直线l距离最小时点P的位置。
画出当P到直线l距离最大时点P的位置。
P
如图①,已知平面内一定点A和一动点B,若AB长度固定,则动点B的轨迹是以点A为圆心,AB长为半径的圆.
图①
寻圆之旅
基本模型 :定点定长作圆
探究1:如右图, 若OA=OB=OC,∠AOB=60°,则∠ACB= 。
总结:OA=OB=OC,则A,B,C三点共圆,常借助圆周角定理来解决角度问题
30°
隐圆概念:
根据问题的需要,通过利用圆的特征添加进题目的圆,也叫辅助圆。它能够帮助我们简化复杂的问题,使求解过程更为直观和简单。
揭秘隐圆
基本思路:把“隐圆”化为“显圆”
探究2:如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点F在边AC上,并且CF=2,点E为边BC上的动点,将△CEF沿EF所在直线翻折,点C落在点P处,则BP的最小值是多少?
揭秘隐圆
总结:在折叠问题中,利用“定点定长作圆”模型确定动点的运动轨迹.
解:由题意得:P点的运动轨迹是以F为圆心,CF长为半径的圆上的一部分。连接BF与圆的交点即为P。
∵BC=8,CF=2,∠FCE=90°
∴
∴BP最小=-2
变式训练:如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点F在边AC上,并且CF=2,点E为边BC上的动点,将△CEF沿EF所在直线翻折,点C落在点P处,求△ABP面积的最小值?
总结:在折叠问题中,利用“定点定长作圆”模型确定动点的运动轨迹.
相信自己我能行
揭秘隐圆
探究3:(2025西峡一模)如图,等边三角形ABC和等边三角形ADE,点N、点M分别为BC、DE的中点,AB=6,AD=4,△ADE绕点A旋转的过程中,MN的最大值为 ,最小值为 。
总结:
在旋转问题中,利用“定点定长作圆”模型确定动点的运动轨迹.
有一架竖直靠在直角墙面的梯子正在下滑,一只猫紧紧盯住位于梯子正中间的老鼠,等待与老鼠距离最小时捕捉.把墙面、梯子、猫和老鼠都理想化为同一平面内的线或点,模型如图,∠ABC=90°,点M,N分别在射线BA,BC上,MN(梯子)长度始终保持不变,MN=4,E(老鼠)为MN的中点,点D(猫)到BA,BC的距离分别为4和2.在此滑动过程中,猫与老鼠的距离DE的最小值为 。
情景问题
通过本节课的研究学习,你学到了哪些知识,有哪些学习的方法,与大家分享一下。
课堂小结
课堂检测
如图,四边形ABCD中,AB=AC=AD,∠CBD=20°,∠BDC=30°,则∠BAD= 。
要求:①独立完成,书写要规范,整齐,字迹要工整,干净。
②组长上交老师批改,组员由组长批改。
课堂检测
或
课堂检测
3、(选做)如图,在矩形ABCD中,AB=3,BC=2,M是边AD的中点,N是AB边上的一动点(不与A点重合),将△AMN沿MN所在直线折叠得到△A’MN,连接A’C,则A’C的最小值是 。
课前准备:
请准备好:导学案、练习本,双色笔, 更重要的是你的激情!
课前寄语:我的课堂,我做主!
相信自己,我是最棒的!
快乐学习,学习快乐!
中考数学第二轮复习
圆的专题复习:隐圆问题(一)
内乡复兴学校 符 青
考情分析
隐圆问题作为几何板块的重要内容,在河南中考试卷上频繁出现,2022年、2024年都出在第15题的位置。
有一架竖直靠在直角墙面的梯子正在下滑,一只猫紧紧盯住位于梯子正中间的老鼠,等待与老鼠距离最小时捕捉.把墙面、梯子、猫和老鼠都理想化为同一平面内的线或点,模型如图,∠ABC=90°,点M,N分别在射线BA,BC上,MN(梯子)长度始终保持不变,MN=4,E(老鼠)为MN的中点,点D(猫)到BA,BC的距离分别为4和2.在此滑动过程中,猫与老鼠的距离DE的最小值为 。
情景问题
复习目标
1.会根据已知条件,确定隐圆模型,并画出隐圆
2.利用隐圆,能解决求角度、线段长及最值等数学问题
3.体会模型,分类讨论等基本数学思想方法
知识储备
1、圆的定义
2、圆周角定理
3、直角三角形的性质 (请同学们大声读背导学案上的内容)
4、点圆最值问题
5、线圆最值问题
九下教材内容
点圆最值问题
已知平面内一定点D和☉O,点E是☉O上一动点,画出当DE最小时点E的位置。
画出当DE最大时点E的位置。
E1
E2
线圆最值问题
已知☉O及直线l,☉O的半径为r,点P为☉O上一动点,
画出当P到直线l距离最小时点P的位置。
画出当P到直线l距离最大时点P的位置。
P
如图①,已知平面内一定点A和一动点B,若AB长度固定,则动点B的轨迹是以点A为圆心,AB长为半径的圆.
图①
寻圆之旅
基本模型 :定点定长作圆
探究1:如右图, 若OA=OB=OC,∠AOB=60°,则∠ACB= 。
总结:OA=OB=OC,则A,B,C三点共圆,常借助圆周角定理来解决角度问题
30°
隐圆概念:
根据问题的需要,通过利用圆的特征添加进题目的圆,也叫辅助圆。它能够帮助我们简化复杂的问题,使求解过程更为直观和简单。
揭秘隐圆
基本思路:把“隐圆”化为“显圆”
探究2:如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点F在边AC上,并且CF=2,点E为边BC上的动点,将△CEF沿EF所在直线翻折,点C落在点P处,则BP的最小值是多少?
揭秘隐圆
总结:在折叠问题中,利用“定点定长作圆”模型确定动点的运动轨迹.
解:由题意得:P点的运动轨迹是以F为圆心,CF长为半径的圆上的一部分。连接BF与圆的交点即为P。
∵BC=8,CF=2,∠FCE=90°
∴
∴BP最小=-2
变式训练:如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点F在边AC上,并且CF=2,点E为边BC上的动点,将△CEF沿EF所在直线翻折,点C落在点P处,求△ABP面积的最小值?
总结:在折叠问题中,利用“定点定长作圆”模型确定动点的运动轨迹.
相信自己我能行
揭秘隐圆
探究3:(2025西峡一模)如图,等边三角形ABC和等边三角形ADE,点N、点M分别为BC、DE的中点,AB=6,AD=4,△ADE绕点A旋转的过程中,MN的最大值为 ,最小值为 。
总结:
在旋转问题中,利用“定点定长作圆”模型确定动点的运动轨迹.
有一架竖直靠在直角墙面的梯子正在下滑,一只猫紧紧盯住位于梯子正中间的老鼠,等待与老鼠距离最小时捕捉.把墙面、梯子、猫和老鼠都理想化为同一平面内的线或点,模型如图,∠ABC=90°,点M,N分别在射线BA,BC上,MN(梯子)长度始终保持不变,MN=4,E(老鼠)为MN的中点,点D(猫)到BA,BC的距离分别为4和2.在此滑动过程中,猫与老鼠的距离DE的最小值为 。
情景问题
通过本节课的研究学习,你学到了哪些知识,有哪些学习的方法,与大家分享一下。
课堂小结
课堂检测
如图,四边形ABCD中,AB=AC=AD,∠CBD=20°,∠BDC=30°,则∠BAD= 。
要求:①独立完成,书写要规范,整齐,字迹要工整,干净。
②组长上交老师批改,组员由组长批改。
课堂检测
或
课堂检测
3、(选做)如图,在矩形ABCD中,AB=3,BC=2,M是边AD的中点,N是AB边上的一动点(不与A点重合),将△AMN沿MN所在直线折叠得到△A’MN,连接A’C,则A’C的最小值是 。
同课章节目录
