1.2.1 函数的概念 教案1
图片预览

文档简介
§1.2.1函数概念的教学设计
一.教学目标
知识要求目标:
1.理解函数的定义、函数的定义域、值域及对应法则。
2.掌握判定函数和函数相等的方法。
3.学会求函数的定义域与函数值。.
能力发展目标:
通过从实际问题中抽象概括出函数概念的活动,培养学生从“特殊到一般”的分析问题的能力,提高学生的抽象概括能力。
情感价值目标:
让学生用函数观点去认知分析现实世界。
二.教学重难点:
重点:函数的概念,函数的三要素。
难点:函数概念及符号y=f(x)的理解。
三.教学导图
分析教材中的三个实例
↓
引出函数的概念
↓
对概念的进一步解读
↙ ↘
根据对概念的分析判定函数 求函数定义域与函数值
↓
根据三要素判定函数相等
↓
课堂小结
↓
课后作业
四.新课讲授
实例(1)一枚炮弹发射后,经过26s落到地面击中目标,炮弹的射高为845m,且炮弹距地面的高度h(单位:m)随时间t(单位:s)变化的规律是h=130t-5 A={t|0≤t≤26},B={h|0≤h≤845}
启发学生用集合与对应的语言描述变量之间的依赖关系:在t的变化范围内,任给一个t,按照给定的解析式,都有唯一的一个高度h与之相对应。
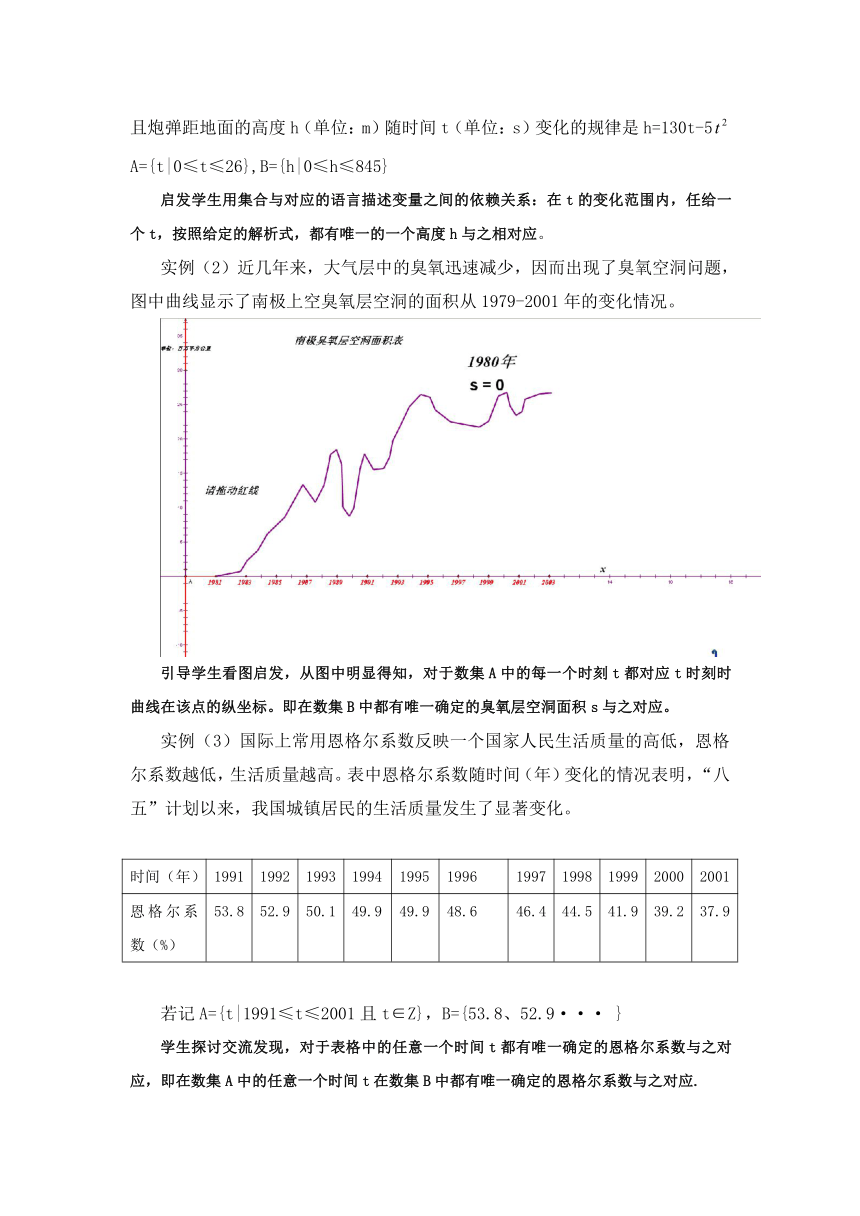
实例(2)近几年来,大气层中的臭氧迅速减少,因而出现了臭氧空洞问题,图中曲线显示了南极上空臭氧层空洞的面积从1979-2001年的变化情况。
引导学生看图启发,从图中明显得知,对于数集A中的每一个时刻t都对应t时刻时曲线在该点的纵坐标。即在数集B中都有唯一确定的臭氧层空洞面积s与之对应。
实例(3)国际上常用恩格尔系数反映一个国家人民生活质量的高低,恩格尔系数越低,生活质量越高。表中恩格尔系数随时间(年)变化的情况表明,“八五”计划以来,我国城镇居民的生活质量发生了显著变化。
时间(年)
1991
1992
1993
1994
1995
1996
1997
1998
1999
2000
2001
恩格尔系数(%)
53.8
52.9
50.1
49.9
49.9
48.6
46.4
44.5
41.9
39.2
37.9
若记A={t|1991≤t≤2001且t∈Z},B={53.8、52.9··· }
学生探讨交流发现,对于表格中的任意一个时间t都有唯一确定的恩格尔系数与之对应,即在数集A中的任意一个时间t在数集B中都有唯一确定的恩格尔系数与之对应.
教师及时提问:这三个实例的共同点?
学生认真思考,在教师启发点拨下,归纳总结
共同点:①都有两个非空数集
②两个数集间都有一种确定的对应关系,即按照这种对应关系对于集合A中任意一个数,在集合B中都有唯一确定的数与之对应。
因此,究其函数的本质,我们用集合和对应的观点给出函数全新的定义。
一般地,设A、B是非空的数集,如果按照某种确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数f(x)和它对应,那么就称 f:A→B为从集合A到集合B的一个函数。记作:y﹦f(x),x∈A。
其中x叫自变量,x的取值范围A叫做函数的定义域 , y叫函数值,y的取值范围C={f(x)|x∈A}叫做函数的值域。
对定义的再解读:
①函数首先是两个非空数集之间建立的对应
②对于x的每一个值,按照某种确定的对应关系f,都有唯一的y值与它对应,这种对应为数与数之间的一一对应或多一对应
③值域是一个集合且值域是集合B的子集(举例:A为学生的学号,B为1-200的整数集,某次百分制的考试学生学号与成绩的对应)
④认真理解y﹦f(x)的含义:f(x)并不表示f与x的乘积,它是一种符号,表示x经f作用后的结果。(具体怎么作用是后面函数表示法的内容,可初步举例:f(x)=)
⑤函数的三要素:定义域,值域和对应法则。
通过例子加深对定义的理解。
例1.判断下列哪些是函数。(考察①②两点)
1.
x
1
2
3
4
5
6
7
8
y
8
7
6
5
4
3
2
1
2.火车站的火车时刻表,不同火车的始发时间和到站时间。
3. x∈﹛x|x≥0﹜
4.
A B A B
f f
-2 2 -2 2
2 0 2 0
0 4 0 4
4 4
6
我们已经学会了如何判定函数,接下来我们就对具体的函数进行分析。
例2.已知函数f(x)=
(1)求函数的定义域。 (2)求f(1),f(2x)
课堂练习P19.1,2(请学生在黑板上解答)
由于函数有三要素,显然两个函数要相等就需要这三个要素全部相同。但由于值域由函数的定义域和对应关系唯一确定。(如同加工厂中,原料(x)确定,加工过程(f)确定,最后加工后的产品(y)也得以确定的。)故我们判断函数相等就只需看定义域和对应法则这两个要素了。
例3.下例函数中哪个与函数y=x相等
(1) (2)
(3) (4)
课堂练习P19.3(请同学单独回答,其它同学给出评价)
课堂小结:理解函数的概念和函数的三要素,会求函数定义域和函数值,会判断函数是否相等。
课后作业:
请找出至少3个生活中存在的函数关系的实例,指出函数三要素;请再找出一个生活实例,说明两个变量之间存在依赖关系,但不是函数。
P24.2,3,4
板书设计
函数的概念
函数的定义
解读①②③④⑤
2,判定函数
3. 定义域和函数值的求法
4. 判断函数是否相等
一.教学目标
知识要求目标:
1.理解函数的定义、函数的定义域、值域及对应法则。
2.掌握判定函数和函数相等的方法。
3.学会求函数的定义域与函数值。.
能力发展目标:
通过从实际问题中抽象概括出函数概念的活动,培养学生从“特殊到一般”的分析问题的能力,提高学生的抽象概括能力。
情感价值目标:
让学生用函数观点去认知分析现实世界。
二.教学重难点:
重点:函数的概念,函数的三要素。
难点:函数概念及符号y=f(x)的理解。
三.教学导图
分析教材中的三个实例
↓
引出函数的概念
↓
对概念的进一步解读
↙ ↘
根据对概念的分析判定函数 求函数定义域与函数值
↓
根据三要素判定函数相等
↓
课堂小结
↓
课后作业
四.新课讲授
实例(1)一枚炮弹发射后,经过26s落到地面击中目标,炮弹的射高为845m,且炮弹距地面的高度h(单位:m)随时间t(单位:s)变化的规律是h=130t-5 A={t|0≤t≤26},B={h|0≤h≤845}
启发学生用集合与对应的语言描述变量之间的依赖关系:在t的变化范围内,任给一个t,按照给定的解析式,都有唯一的一个高度h与之相对应。
实例(2)近几年来,大气层中的臭氧迅速减少,因而出现了臭氧空洞问题,图中曲线显示了南极上空臭氧层空洞的面积从1979-2001年的变化情况。
引导学生看图启发,从图中明显得知,对于数集A中的每一个时刻t都对应t时刻时曲线在该点的纵坐标。即在数集B中都有唯一确定的臭氧层空洞面积s与之对应。
实例(3)国际上常用恩格尔系数反映一个国家人民生活质量的高低,恩格尔系数越低,生活质量越高。表中恩格尔系数随时间(年)变化的情况表明,“八五”计划以来,我国城镇居民的生活质量发生了显著变化。
时间(年)
1991
1992
1993
1994
1995
1996
1997
1998
1999
2000
2001
恩格尔系数(%)
53.8
52.9
50.1
49.9
49.9
48.6
46.4
44.5
41.9
39.2
37.9
若记A={t|1991≤t≤2001且t∈Z},B={53.8、52.9··· }
学生探讨交流发现,对于表格中的任意一个时间t都有唯一确定的恩格尔系数与之对应,即在数集A中的任意一个时间t在数集B中都有唯一确定的恩格尔系数与之对应.
教师及时提问:这三个实例的共同点?
学生认真思考,在教师启发点拨下,归纳总结
共同点:①都有两个非空数集
②两个数集间都有一种确定的对应关系,即按照这种对应关系对于集合A中任意一个数,在集合B中都有唯一确定的数与之对应。
因此,究其函数的本质,我们用集合和对应的观点给出函数全新的定义。
一般地,设A、B是非空的数集,如果按照某种确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数f(x)和它对应,那么就称 f:A→B为从集合A到集合B的一个函数。记作:y﹦f(x),x∈A。
其中x叫自变量,x的取值范围A叫做函数的定义域 , y叫函数值,y的取值范围C={f(x)|x∈A}叫做函数的值域。
对定义的再解读:
①函数首先是两个非空数集之间建立的对应
②对于x的每一个值,按照某种确定的对应关系f,都有唯一的y值与它对应,这种对应为数与数之间的一一对应或多一对应
③值域是一个集合且值域是集合B的子集(举例:A为学生的学号,B为1-200的整数集,某次百分制的考试学生学号与成绩的对应)
④认真理解y﹦f(x)的含义:f(x)并不表示f与x的乘积,它是一种符号,表示x经f作用后的结果。(具体怎么作用是后面函数表示法的内容,可初步举例:f(x)=)
⑤函数的三要素:定义域,值域和对应法则。
通过例子加深对定义的理解。
例1.判断下列哪些是函数。(考察①②两点)
1.
x
1
2
3
4
5
6
7
8
y
8
7
6
5
4
3
2
1
2.火车站的火车时刻表,不同火车的始发时间和到站时间。
3. x∈﹛x|x≥0﹜
4.
A B A B
f f
-2 2 -2 2
2 0 2 0
0 4 0 4
4 4
6
我们已经学会了如何判定函数,接下来我们就对具体的函数进行分析。
例2.已知函数f(x)=
(1)求函数的定义域。 (2)求f(1),f(2x)
课堂练习P19.1,2(请学生在黑板上解答)
由于函数有三要素,显然两个函数要相等就需要这三个要素全部相同。但由于值域由函数的定义域和对应关系唯一确定。(如同加工厂中,原料(x)确定,加工过程(f)确定,最后加工后的产品(y)也得以确定的。)故我们判断函数相等就只需看定义域和对应法则这两个要素了。
例3.下例函数中哪个与函数y=x相等
(1) (2)
(3) (4)
课堂练习P19.3(请同学单独回答,其它同学给出评价)
课堂小结:理解函数的概念和函数的三要素,会求函数定义域和函数值,会判断函数是否相等。
课后作业:
请找出至少3个生活中存在的函数关系的实例,指出函数三要素;请再找出一个生活实例,说明两个变量之间存在依赖关系,但不是函数。
P24.2,3,4
板书设计
函数的概念
函数的定义
解读①②③④⑤
2,判定函数
3. 定义域和函数值的求法
4. 判断函数是否相等
