1.2.2 函数的表示法 课件1(第1课时)
文档属性
| 名称 | 1.2.2 函数的表示法 课件1(第1课时) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-08-02 13:25:54 | ||
图片预览





文档简介
课件14张PPT。1.2.2 函数的表示法
第1课时 函数的表示法1.掌握函数的三种表示法:解析法、列表法、
图象法,体会三种表示方法的优点.(重点)
2.分段函数及其应用.(难点)思考:初中学习了函数的哪几种表示方法?数学表达式图象表格例1 某种笔记本的单价是5元,买 个笔记本需要y元.试用函数的三种表示法表示函数
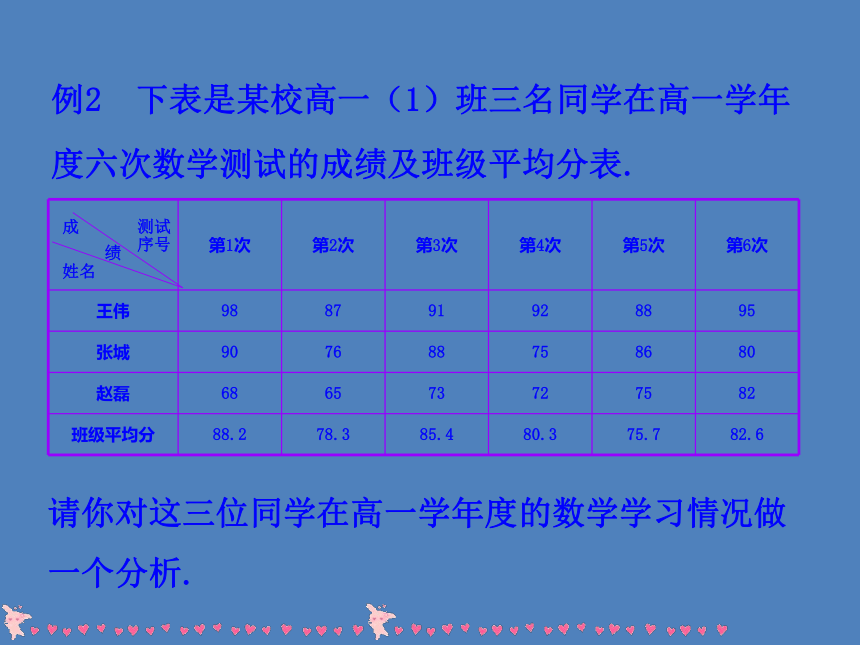
y=f(x).解:这个函数的定义域是数集{1,2,3,4,5}列表法表示如下:用图象法可将函数表示为右图:用解析法表示为函数的图象既可以是连续的曲线,也可以是直线、折线、离散的点等等。(1)用解析法表示函数是否一定要写出自变量的取值范围?(2)用描点法画函数图象的一般步骤是什么?列表、描点、连线(视其定义域决定是否连线)函数的定义域是函数存在的前提,写函数解析式的时候,一般要写出函数的定义域.例2 下表是某校高一(1)班三名同学在高一学年度六次数学测试的成绩及班级平均分表. 请你对这三位同学在高一学年度的数学学习情况做一个分析.测试
序号成
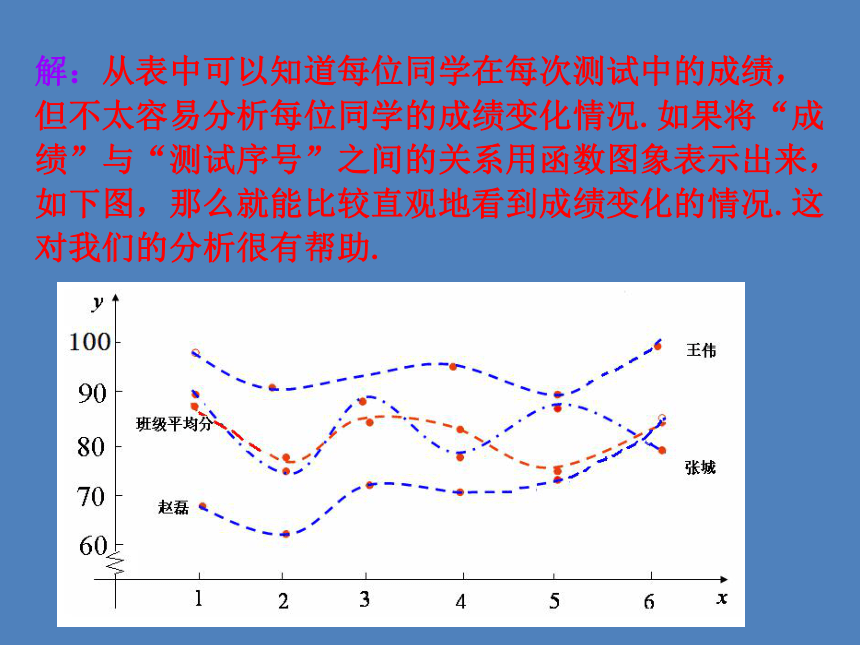
绩姓名解:从表中可以知道每位同学在每次测试中的成绩,但不太容易分析每位同学的成绩变化情况.如果将“成绩”与“测试序号”之间的关系用函数图象表示出来,如下图,那么就能比较直观地看到成绩变化的情况.这对我们的分析很有帮助.【知识点拨】
函数三种表示方法的优缺点
(1)解析法.
优点:①简明、全面概述变量之间的关系;
②利用解析式可以求任意函数值.
缺点:不够形象、直观,并且不是每一个函数都有 解析式.
(2)图象法.
优点:能形象直观表示函数的变化情况.
缺点:只能近似求出函数值且有时误差较大.
(3)列表法.
优点:不用计算可直接看出与自变量对应的函数值.
缺点:仅能表示自变量取较少的有限值时的函数值.
1. 画出下列函数的图象:
(1)
(2)解:(1)(2)【变式练习】在它的定义域中,对于自变量的不同取值范围,对应关系不同.例3 画出函数 的图象.探究2 分段函数 有些函数在它的定义域中,对于自变量的
不同取值范围,对应关系不同,这种函数通常
称为_________.分段函数注意(1)分段函数是一个函数,不要把它误认为是几个函数;
(2)分段函数的定义域是各段定义域的并集,值域是各段值域的并集. 例4 某市“招手即停”公共汽车的票价按下列规则制定:
(1)5公里以内(含5公里),票价2元;
(2)5公里以上,每增加5公里,票价增加1元(不足5公里的按5公里计算).
如果某条线路的总里程为20公里,请根据题意,
写出票价与里程之间的函数解析式,并画出函数的图象.3.求分段函数的解析式y=2, 03, 5 < x ≤ 10
4, 10 < x ≤ 15
5, 15 < x≤20解:设票价为y元,里程为x公里,由题意可知,自变量x
的取值范围是(0,20]
由“招手即停”公共汽车票价的制定规定,可得到以下
函数解析式:根据这个函数解析式,
可画出函数图象,
如右图:y○2O51015201345x○○○练习:
1.求分段函数的函数值: 已知函数f(x)=x+2, x≤-1;x2, -1<x<2;2x, x≥2.(2)若f(x)=3,求x的值.(1)求 的值;解:(1)(2)2.某路公共汽车,行进的站数与票价关系如下表:此函数关系除了用列表法表示之外,能否用其他方法表示?解:
第1课时 函数的表示法1.掌握函数的三种表示法:解析法、列表法、
图象法,体会三种表示方法的优点.(重点)
2.分段函数及其应用.(难点)思考:初中学习了函数的哪几种表示方法?数学表达式图象表格例1 某种笔记本的单价是5元,买 个笔记本需要y元.试用函数的三种表示法表示函数
y=f(x).解:这个函数的定义域是数集{1,2,3,4,5}列表法表示如下:用图象法可将函数表示为右图:用解析法表示为函数的图象既可以是连续的曲线,也可以是直线、折线、离散的点等等。(1)用解析法表示函数是否一定要写出自变量的取值范围?(2)用描点法画函数图象的一般步骤是什么?列表、描点、连线(视其定义域决定是否连线)函数的定义域是函数存在的前提,写函数解析式的时候,一般要写出函数的定义域.例2 下表是某校高一(1)班三名同学在高一学年度六次数学测试的成绩及班级平均分表. 请你对这三位同学在高一学年度的数学学习情况做一个分析.测试
序号成
绩姓名解:从表中可以知道每位同学在每次测试中的成绩,但不太容易分析每位同学的成绩变化情况.如果将“成绩”与“测试序号”之间的关系用函数图象表示出来,如下图,那么就能比较直观地看到成绩变化的情况.这对我们的分析很有帮助.【知识点拨】
函数三种表示方法的优缺点
(1)解析法.
优点:①简明、全面概述变量之间的关系;
②利用解析式可以求任意函数值.
缺点:不够形象、直观,并且不是每一个函数都有 解析式.
(2)图象法.
优点:能形象直观表示函数的变化情况.
缺点:只能近似求出函数值且有时误差较大.
(3)列表法.
优点:不用计算可直接看出与自变量对应的函数值.
缺点:仅能表示自变量取较少的有限值时的函数值.
1. 画出下列函数的图象:
(1)
(2)解:(1)(2)【变式练习】在它的定义域中,对于自变量的不同取值范围,对应关系不同.例3 画出函数 的图象.探究2 分段函数 有些函数在它的定义域中,对于自变量的
不同取值范围,对应关系不同,这种函数通常
称为_________.分段函数注意(1)分段函数是一个函数,不要把它误认为是几个函数;
(2)分段函数的定义域是各段定义域的并集,值域是各段值域的并集. 例4 某市“招手即停”公共汽车的票价按下列规则制定:
(1)5公里以内(含5公里),票价2元;
(2)5公里以上,每增加5公里,票价增加1元(不足5公里的按5公里计算).
如果某条线路的总里程为20公里,请根据题意,
写出票价与里程之间的函数解析式,并画出函数的图象.3.求分段函数的解析式y=2, 0
4, 10 < x ≤ 15
5, 15 < x≤20解:设票价为y元,里程为x公里,由题意可知,自变量x
的取值范围是(0,20]
由“招手即停”公共汽车票价的制定规定,可得到以下
函数解析式:根据这个函数解析式,
可画出函数图象,
如右图:y○2O51015201345x○○○练习:
1.求分段函数的函数值: 已知函数f(x)=x+2, x≤-1;x2, -1<x<2;2x, x≥2.(2)若f(x)=3,求x的值.(1)求 的值;解:(1)(2)2.某路公共汽车,行进的站数与票价关系如下表:此函数关系除了用列表法表示之外,能否用其他方法表示?解:
