2.2 直线与平面平行的判定 学案2(第1课时,无答案)
文档属性
| 名称 | 2.2 直线与平面平行的判定 学案2(第1课时,无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 75.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-08-02 00:00:00 | ||
图片预览

文档简介
2.2.1 直线与平面平行的判定
预 习 案
要点1
类型
文字语言
图形语言
符号语言
直线与平面平行
的一条直线与 的一条直线 ,则该直线与平面平行
a?α,b?α,且a∥b,则a∥α
1.一条直线平行于平面内无数条直线,则该直线与这个平面平行吗?
探究案
题型一 理解线面平行
例1 给出以下四个命题:
①如果一条直线和一个平面平行,那么这条直线和平面内的任意一条直线平行;
②过平面外一点有且只有一条直线与平面平行;
③如果一条直线上有两点到一个平面内的距离相等,那么这条直线平行于该平面;
④如果两条平行线中有一条平行于这个平面,那么另外一条直线也平行于该平面.
其中真命题的个数是( )
A.0 B.1 C.2 D.3
思考题1 能保证直线a与平面α平行的条件是( )
A.b?α,a∥b
B.b?α,c∥α,a∥b,a∥c
C.b?α,A、B∈a,C、D∈b且AC=BD
D.a?α,b?α,a∥b
题型二 中位线法证线面平行
例2 如图所示,在直三棱柱ABC-A1B1C1中,AC=BC,
点D是AB的中点,求证:BC1∥平面CA1D.
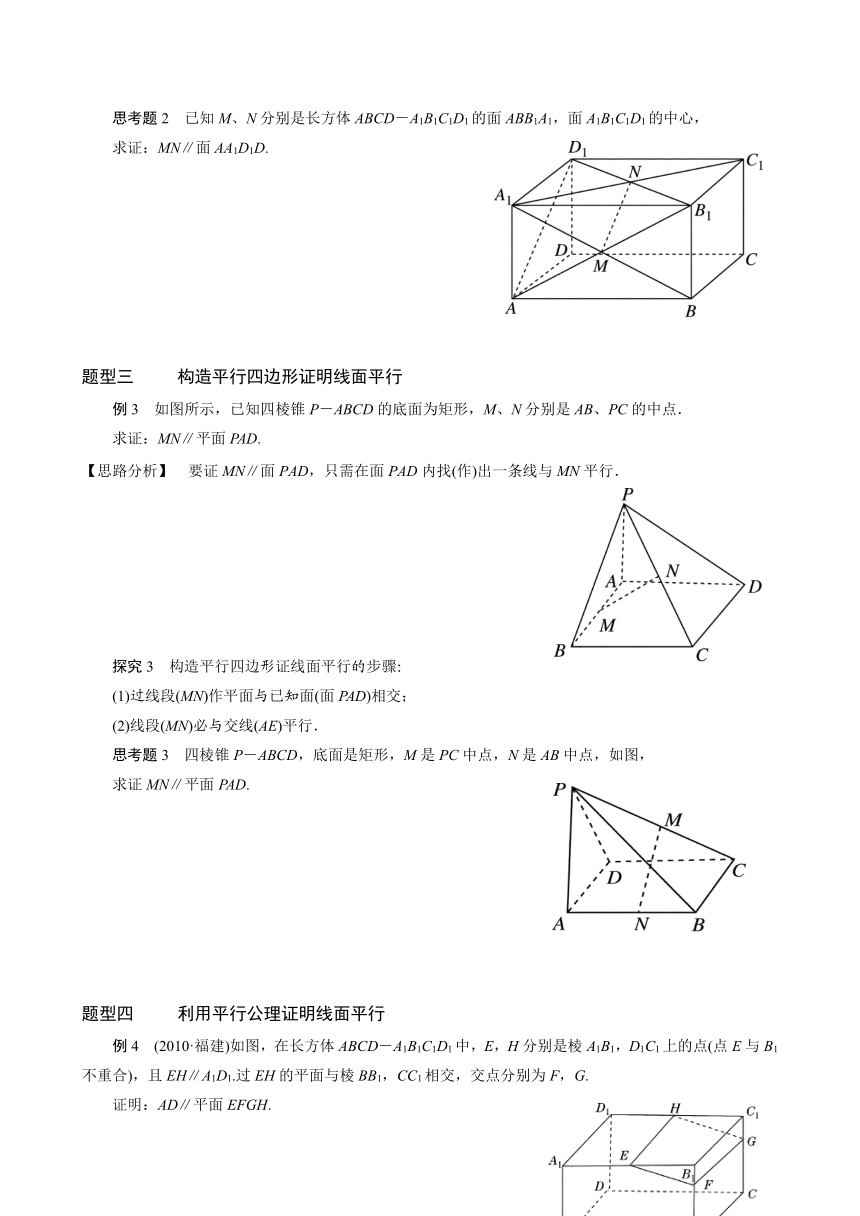
思考题2 已知M、N分别是长方体ABCD-A1B1C1D1的面ABB1A1,面A1B1C1D1的中心,
求证:MN∥面AA1D1D.
题型三 构造平行四边形证明线面平行
例3 如图所示,已知四棱锥P-ABCD的底面为矩形,M、N分别是AB、PC的中点.
求证:MN∥平面PAD.
【思路分析】 要证MN∥面PAD,只需在面PAD内找(作)出一条线与MN平行.
探究3 构造平行四边形证线面平行的步骤:
(1)过线段(MN)作平面与已知面(面PAD)相交;
(2)线段(MN)必与交线(AE)平行.
思考题3 四棱锥P-ABCD,底面是矩形,M是PC中点,N是AB中点,如图,
求证MN∥平面PAD.
题型四 利用平行公理证明线面平行
例4 (2010·福建)如图,在长方体ABCD-A1B1C1D1中,E,H分别是棱A1B1,D1C1上的点(点E与B1不重合),且EH∥A1D1.过EH的平面与棱BB1,CC1相交,交点分别为F,G.
证明:AD∥平面EFGH.
【思路分析】 要证AD∥面EFGH只需利用已知条件证得AD∥EH.
探究4 (1)当多条线平行时,可利用平行线的传递性.
(2)平行线的传递性常用于构造并证明平行四边形中.
思考题4 (2010·陕西高考改编)如图,在四棱锥P-ABCD中,底面ABCD是矩形,E,F分别是PB, PC的中点.证明:EF∥平面PAD.
题型五 利用平行线分线段成比例证线面平行
例5 如图,正方体ABCD-A1B1C1D1中,点N在BD上,点M在B1C上,且CM=DN,
求证:MN∥平面AA1B1B.
思考题5 正四棱锥P-ABCD的各条棱长都是13,M、N分别是PA和BD上的点,且PM∶MA=BN∶ND=5∶8.
求证:MN∥平面PBC.
课堂小结
1.判定线线平行的方法:
①三角形中位线;②平行四边形法;③平行线分线段成比例;④平行公理;⑤两条线垂直于同一个平面;⑥线面平行的性质定理;⑦面面平行的性质定理.
2.判定线面平行的方法:
①判定定理;②面面平行.
预 习 案
要点1
类型
文字语言
图形语言
符号语言
直线与平面平行
的一条直线与 的一条直线 ,则该直线与平面平行
a?α,b?α,且a∥b,则a∥α
1.一条直线平行于平面内无数条直线,则该直线与这个平面平行吗?
探究案
题型一 理解线面平行
例1 给出以下四个命题:
①如果一条直线和一个平面平行,那么这条直线和平面内的任意一条直线平行;
②过平面外一点有且只有一条直线与平面平行;
③如果一条直线上有两点到一个平面内的距离相等,那么这条直线平行于该平面;
④如果两条平行线中有一条平行于这个平面,那么另外一条直线也平行于该平面.
其中真命题的个数是( )
A.0 B.1 C.2 D.3
思考题1 能保证直线a与平面α平行的条件是( )
A.b?α,a∥b
B.b?α,c∥α,a∥b,a∥c
C.b?α,A、B∈a,C、D∈b且AC=BD
D.a?α,b?α,a∥b
题型二 中位线法证线面平行
例2 如图所示,在直三棱柱ABC-A1B1C1中,AC=BC,
点D是AB的中点,求证:BC1∥平面CA1D.
思考题2 已知M、N分别是长方体ABCD-A1B1C1D1的面ABB1A1,面A1B1C1D1的中心,
求证:MN∥面AA1D1D.
题型三 构造平行四边形证明线面平行
例3 如图所示,已知四棱锥P-ABCD的底面为矩形,M、N分别是AB、PC的中点.
求证:MN∥平面PAD.
【思路分析】 要证MN∥面PAD,只需在面PAD内找(作)出一条线与MN平行.
探究3 构造平行四边形证线面平行的步骤:
(1)过线段(MN)作平面与已知面(面PAD)相交;
(2)线段(MN)必与交线(AE)平行.
思考题3 四棱锥P-ABCD,底面是矩形,M是PC中点,N是AB中点,如图,
求证MN∥平面PAD.
题型四 利用平行公理证明线面平行
例4 (2010·福建)如图,在长方体ABCD-A1B1C1D1中,E,H分别是棱A1B1,D1C1上的点(点E与B1不重合),且EH∥A1D1.过EH的平面与棱BB1,CC1相交,交点分别为F,G.
证明:AD∥平面EFGH.
【思路分析】 要证AD∥面EFGH只需利用已知条件证得AD∥EH.
探究4 (1)当多条线平行时,可利用平行线的传递性.
(2)平行线的传递性常用于构造并证明平行四边形中.
思考题4 (2010·陕西高考改编)如图,在四棱锥P-ABCD中,底面ABCD是矩形,E,F分别是PB, PC的中点.证明:EF∥平面PAD.
题型五 利用平行线分线段成比例证线面平行
例5 如图,正方体ABCD-A1B1C1D1中,点N在BD上,点M在B1C上,且CM=DN,
求证:MN∥平面AA1B1B.
思考题5 正四棱锥P-ABCD的各条棱长都是13,M、N分别是PA和BD上的点,且PM∶MA=BN∶ND=5∶8.
求证:MN∥平面PBC.
课堂小结
1.判定线线平行的方法:
①三角形中位线;②平行四边形法;③平行线分线段成比例;④平行公理;⑤两条线垂直于同一个平面;⑥线面平行的性质定理;⑦面面平行的性质定理.
2.判定线面平行的方法:
①判定定理;②面面平行.
