完全平方公式

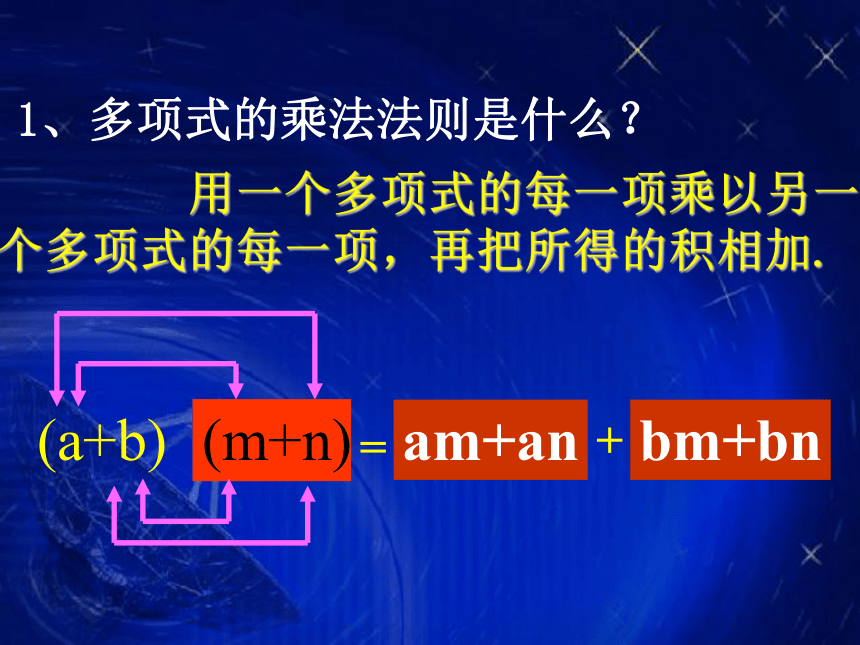
课件18张PPT。 用一个多项式的每一项乘以另一个多项式的每一项，再把所得的积相加.1、多项式的乘法法则是什么？ am+anbm+bn+=(m+n)(a+b)乘法公式----完全平方公式baba(a+b)2a2b2abab=a2+2ab+b2完全平方公式(a-b)2
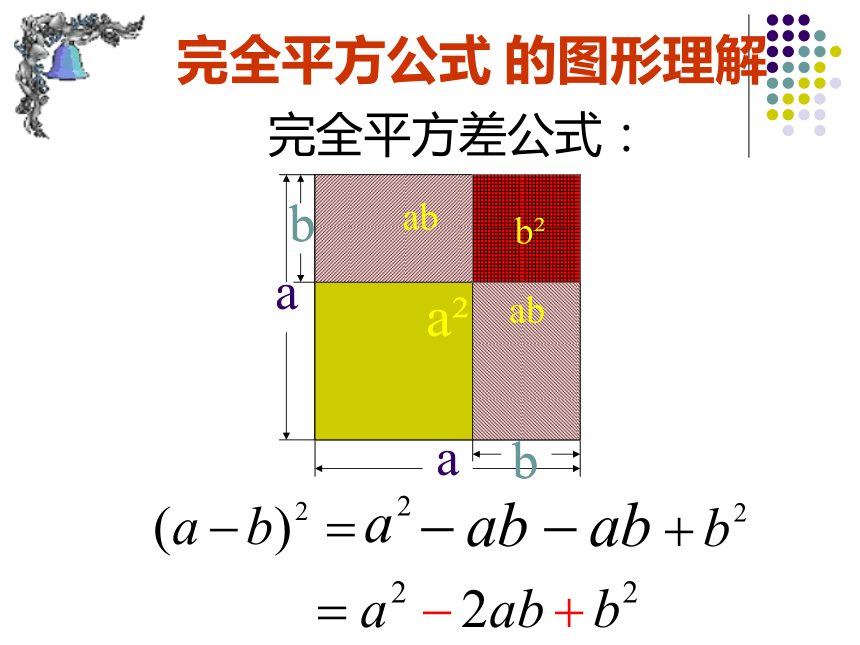
(a-b)2b2完全平方差公式：完全平方公式 的图形理解公式特点：4、公式中的字母a，b可以表示数，单项式和
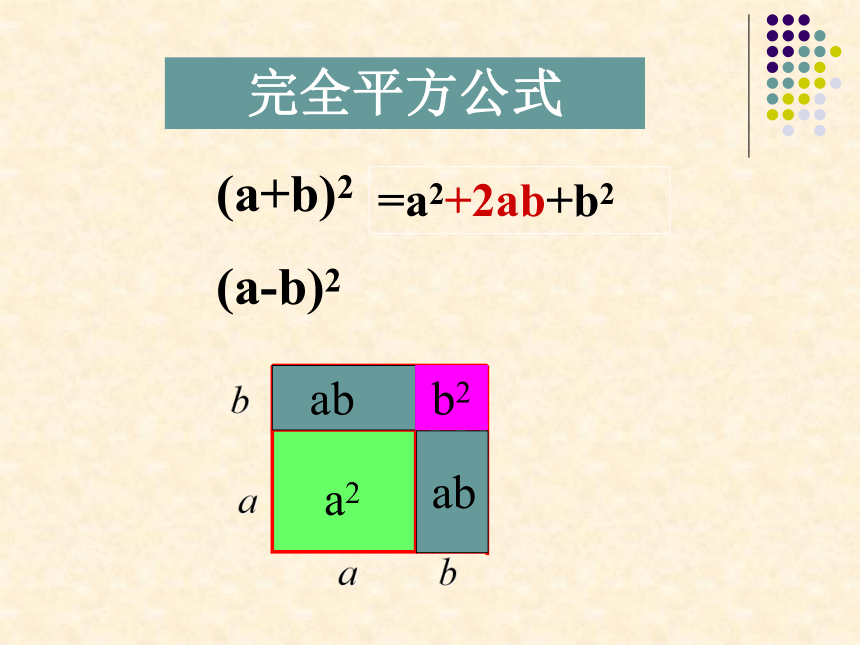
多项式。(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b21、积为二次三项式；2、积中两项为两数的平方和；3、另一项是两数积的2倍，且与乘式中
间的符号相同。首平方，尾平方，积的2倍在中央 计算 (a-b)2 = ？
你是怎样推导的呢？ ( a – b ) 2
= [a +(-b) ] 2= a2 - 2ab + b2=a2 + 2a(-b) + (-b)2例1 运用完全平方公式计算：解： (x+2y)2==x2(1)(x+2y)2(a +b)2= a2 + 2 ab + b2x2+2?x ?2y+(2y)2+4xy+4y2= x2 – 2xy2+4y4(2) ( x – 2y2)2+(2y2)2解：( x – 2y2)2 =(a - b)2 = a2 - 2ab + b2 ( x)2– 2 ?( x) ?(2y2)
是 与 和的平方=（ ）+（ ）（ ）+（ ）是 与 差的平方=（ ）－ （ ）（ ）+（ ）填空：X2yx2y22X5y22x5y(a+b)2=a2+2ab+b2 (a–b)2=a2-2ab+b2=(4x)2+2(4x)(5y)+(5y)2=4x2-12x+9=m2n2-2mna+a2(3) (mn - a) 2(2) (2x - 3) 2 =16x2+40xy+25y2例1：
(1)（4x + 5y) 2-++-结论*首尾平方总得正； **中间符号看首尾，同号得正，异号得负 ***中间两倍 要记牢a3y-2st-3x4ya3a+3yy--2s-2stt+-3x-3x4y4y-例2: 用完全平方公式计算(1) (-2s+t)2(2) (-3x-4y)2=(-2s)2+2(-2s)t+t2=(-3x)2-2(-3x)(4y)+(4y)2=4s2-4st+t2=9x2+24xy+16y2 讨论：
1. (x-2y)(-2y+x) 2. (1-2x)(-2x-1)解：注意平方差公式和完全平方公式的区别.(-a+b)(a-b)判断正误，并改正
(1)(a+b )2=a2 +b2 (2) (a –b) 2 = a2 - b2 (3) ( a +2 b ) 2 = a2 + 2 ab + 2 b2
填空：（1）a2 +b 2+ ______=( a + b ) 2
（2）a2 + b2 + _____ =( a – b ) 2
（3) x2 +4xy +4 y2 = (________) 2
(4) x2 - 4xy +4 y2 = (________) 2

442ab(-2ab)x+2yx-2y例2：运用完全平方公式计算：
解：练习：19139/420.5拓展提高：
如果多项式x2 + kx +25是完全平方式，求k的值填空：若多项式m2 + km +36是完全平方式，则k = ______±12K=±10课时小结完全平方公式 ( a + b ) 2 = a2 + 2ab + b2
( a – b ) 2 = a2 - 2ab + b2
结构特征：(首 ± 尾)2 = 首2 ± 2 ×首×尾 +尾2
口诀：首平方，尾平方，首尾二倍中间放
步骤（1）确定首尾，分别平方
（2）确定中间系数与符号完全平方公式 ( a + b ) 2 = a2 + 2ab + b2
( a – b ) 2 = a2 - 2ab + b2
结构特征：(首 ± 尾)2 = 首2 ± 2 ×首×尾 +尾2
口诀：首平方，尾平方，首尾二倍中间放
步骤（1）确定首尾，分别平方
（2）确定中间系数与符号