【2025秋人教九上数学情境课堂教学课件】22.1.2 二次函数y=ax^2的图象和性质 课件(共27张PPT)
文档属性
| 名称 | 【2025秋人教九上数学情境课堂教学课件】22.1.2 二次函数y=ax^2的图象和性质 课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-26 11:33:16 | ||
图片预览





文档简介
(共27张PPT)
人教新版 九上 数学
同步课件
2025年秋人教九上数学情境课堂教学课件
第二十二章 二次函数
22.1 二次函数的图象和性质
21.1.2 二次函数y=ax 的图象和性质
1. 会用描点法画出形如 y=ax 的二次函数图象,了解抛物线的有关概念.
2. 通过观察图象能说出二次函数 y=ax 的图象特征和性质.
3. 在类比探究二次函数 y=ax 的图象和性质的过程中,进一步体会研究函数图象和性质的基本方法和数形结合的思想.
重点
难点
1. 八年级我们学习了一次函数的什么内容?顺序是什么?
概念
图象
性质
2. 还记得如何研究图象和性质的吗?
列表、描点、连线 函数图象 图象的性质;
思考 (1)二次函数的图象是否仍是一条直线呢?若不是,那是什么呢?
(2)系数的符号(正负)与函数图象、性质是否有关呢?
本节课我们将从最简单的二次函数 y=x 开始,逐步深入地讨论一般二次函数的图象和性质.
做一做 画出二次函数 y=x 的图象.
1.列表:在 y = x2 中,自变量 x 可以是任意实数,
列表表示几组对应值;
9
4
1
0
1
4
9
为了便于计算和图象的准确性,我们取的x和y均为整数
x ... -3 -2 -1 0 1 2 3 ...
y = x2 ... ...
还记得如何用描点法画一个函数的图象吗?
点击查看:会变化的二次函数y=ax2的图象
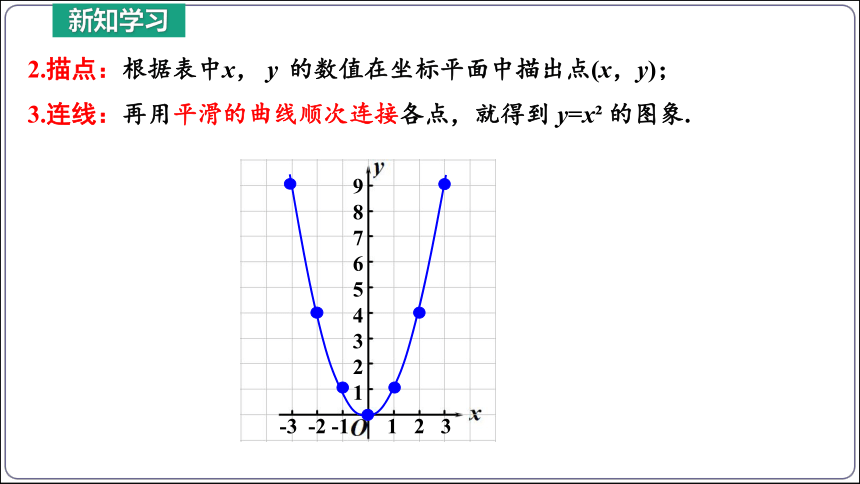
2.描点:根据表中x, y 的数值在坐标平面中描出点(x,y);
3.连线:再用平滑的曲线顺次连接各点,就得到 y=x 的图象.
-3 -2 -1 1 2 3
9
8
7
6
5
4
3
2
1
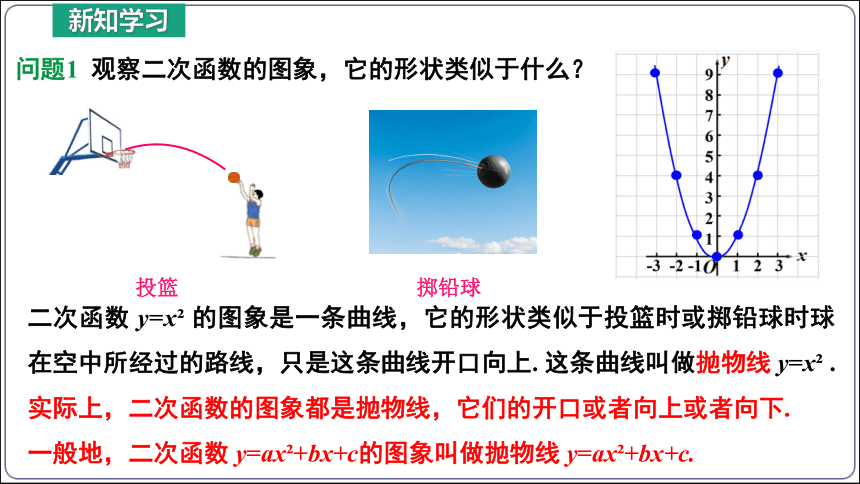
问题1 观察二次函数的图象,它的形状类似于什么?
投篮
掷铅球
二次函数 y=x 的图象是一条曲线,它的形状类似于投篮时或掷铅球时球在空中所经过的路线,只是这条曲线开口向上. 这条曲线叫做抛物线 y=x .
实际上,二次函数的图象都是抛物线,它们的开口或者向上或者向下.
一般地,二次函数 y=ax +bx+c的图象叫做抛物线 y=ax +bx+c.
-3 -2 -1 1 2 3
9
8
7
6
5
4
3
2
1
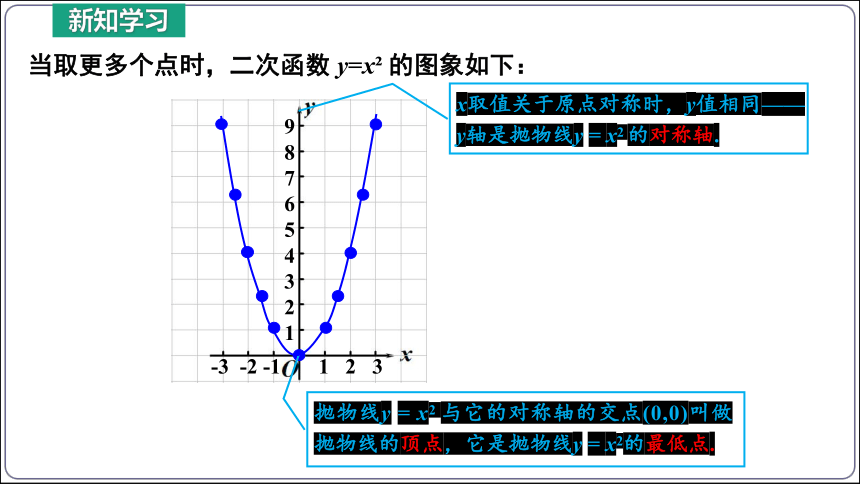
抛物线y = x2 与它的对称轴的交点(0,0)叫做抛物线的顶点,它是抛物线y = x2的最低点.
x取值关于原点对称时,y值相同——y轴是抛物线y = x2 的对称轴.
当取更多个点时,二次函数 y=x 的图象如下:
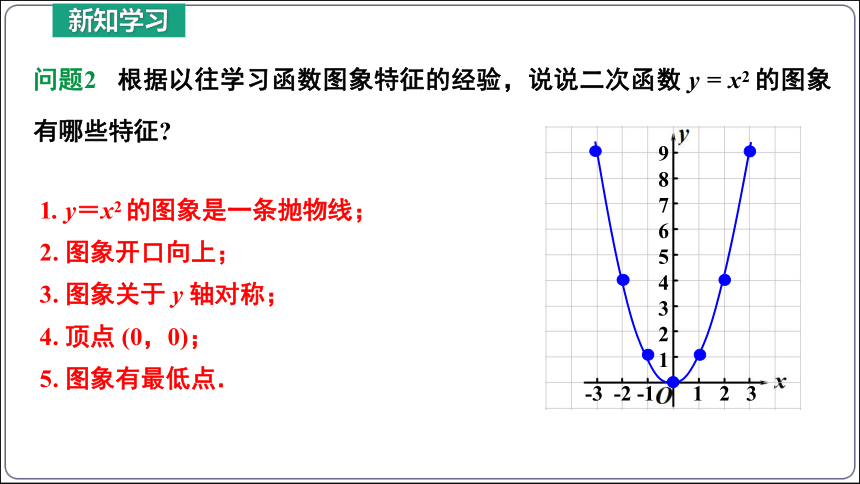
问题2 根据以往学习函数图象特征的经验,说说二次函数 y = x2 的图象有哪些特征
1. y=x2 的图象是一条抛物线;
2. 图象开口向上;
3. 图象关于 y 轴对称;
4. 顶点 (0,0);
5. 图象有最低点.
-3 -2 -1 1 2 3
9
8
7
6
5
4
3
2
1
问题3 观察二次函数 y=x 的图象,y 随 x 如何变化?
从二次函数 y=x 的图象可以看出:
在对称轴的左侧,抛物线从左到右下降→当 x<0 时,y 随 x 的增大而减小;
在对称轴的右侧,抛物线从左到右上升→当 x>0 时,y 随 x 的增大而增大.
-3 -2 -1 1 2 3
9
8
7
6
5
4
3
2
1
例1 在同一直角坐标系中,画出函数 ,y=2x2的图象.
8
4.5
2
0.5
0
0.5
2
x ... -4 -3 -2 -1 0 1 2 3 4 ...
... ...
1.列表:
4.5
8
x ... -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 ...
y=2x2 ... ...
8
4.5
2
0.5
0
0.5
2
4.5
8
2.描点:
3.连线:
-4 -2 2 4
8
6
4
2
问题4 函数 ,y=2x2的图象与函数 y=x2 的图象相比,有什么共同点和不同点?
-4 -2 2 4
8
6
4
2
共同点:开口向上,对称轴是 y 轴,顶点是原点;
不同点:开口大小不同, x2的系数越大,抛物线的开口越小.
二次函数
a的符号
图象
开口方向
顶点坐标
对称轴
增减性
最值
问题5 当a>0时,二次函数 y=ax2 的图象有什么特点?
y=ax2(a≠0)
a>0
向上
(0,0)
y轴
在对称轴的左侧(即x<0),y随x的增大而减小
在对称轴的右侧(即x>0),y随x的增大而增大
当x=0时,
a越大,抛物线的开口越小.
-9
-4
-1
0
-1
-4
-9
x ... -3 -2 -1 0 1 2 3 ...
y = -x2 ... ...
1.列表:
做一做 画出二次函数 y =- x2, ,y=-2x2 的图象.
-8
-4.5
-2
-0.5
0
-0.5
-2
x ... -4 -3 -2 -1 0 1 2 3 4 ...
... ...
-4.5
-8
x ... -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 ...
y=-2x2 ... ...
-8
-4.5
-2
-0.5
0
-0.5
-2
-4.5
-8
2.描点:
3.连线:
y =- x2
问题6 函数 y=-x2, ,y=-2x2的图象之间,有什么共同点和不同点?
共同点:开口向下,对称轴是 y 轴,顶点是原点;
不同点:开口大小不同, x2的系数越小,抛物线的开口越小.
二次函数
a的符号
图象
开口方向
顶点坐标
对称轴
增减性
最值
y=ax2(a≠0)
a<0
向下
(0,0)
y轴
在对称轴的左侧(即x<0),y随x的增大而增大
在对称轴的右侧(即x>0),y随x的增大而减小
问题7 当a<0时,二次函数y=ax2的图象有什么特点?
当x=0时,
a越小,抛物线的开口越小.
问题8 观察右边图象,抛物线y =ax2与y =-ax2 (a>0) 的图象有什么特点?
二次项系数互为相反数时,开口方向相反,开口大小相同,它们关于x轴对称.
|a|越大,抛物线的开口越小.
y =- x2
变式 二次函数y =ax2 与y =-2x2 的形状相同,开口大小一样,开口方向相反,则a=_____.
2
例2 夕夕用软件绘制抛物线 y =4x2 时,将“4”按成了“5”,和原图象相比,发生改变的是( )
A.开口方向 B.开口大小
C.对称轴 D.顶点坐标
B
1.(2024广东)若点(0,y1),(1,y2),(2,y3)都在二次函数y=x2的图象上,则( )
A. y3>y2>y1
B. y2>y1>y3
C. y1>y3>y2
D. y3>y1>y2
A
解:根据题意,得k+2≠0且k2+k-4=2,
解得k1=-3,k2=2,
∵当x<0时,y随x的增大而增大,
∴二次函数的图象的开口向下,即k+2<0,
∴k=-3.
2.已知函数 是二次函数,且当x<0时,y随x的增大而增大.
(1)求k的值;
(2)直接写出顶点坐标和对称轴.
(2)由(1)得y=-x2,
∴顶点坐标为(0,0),对称轴为y轴.
3. 已知二次函数 y = x2,若 x≥m 时,y 最小值为 0,求实数 m 的取值范围.
解:在二次函数 y = x2 中,
当 x = 0 时,y 有最小值,且 y最小值 = 0.
∵ 当 x≥m 时,y最小值 = 0,
∴ m≤0.
4.已知:如图,直线 y=3x+4 与抛物线 y=x2 交于 A、B 两点,求出 A、B 两点的坐标,并求出两交点与原点所围成的三角形的面积
B
解:由题意的
解得 或
∴ 此两函数的交点坐标为A (4,16),B ( 1,1).
∵ 直线 y=3x+4 与 y 轴相交于点 C (0,4),即 CO=4,
∴
∴ S△ABO=S△ACO+S△BOC=10.
二次函数 y=ax2(a≠0) a的符号 a>0 a<0
图象
顶点坐标 对称轴 增减性
最值
1.二次函数y=ax2的图象和性质:
(0,0)
y轴
当x=0时,y最小值=0
当x= 0时,y最大值=0
在对称轴的左侧(即x<0),y随x的增大而减小;在对称轴的右侧(即x>0),y随x的增大而增大
在对称轴的左侧(即x<0),y随x的增大而增大;在对称轴的右侧(即x>0),y随x的增大而减小
y=ax2
a 的符号决
定开口方向
的大小决
定开口大小
a>0,
开口
向上
a<0,
开口
向下
越大,
开口越小
2.二次函数y=ax2的开口方向及大小:
Thanks!
https://www.21cnjy.com/recruitment/home/fine
人教新版 九上 数学
同步课件
2025年秋人教九上数学情境课堂教学课件
第二十二章 二次函数
22.1 二次函数的图象和性质
21.1.2 二次函数y=ax 的图象和性质
1. 会用描点法画出形如 y=ax 的二次函数图象,了解抛物线的有关概念.
2. 通过观察图象能说出二次函数 y=ax 的图象特征和性质.
3. 在类比探究二次函数 y=ax 的图象和性质的过程中,进一步体会研究函数图象和性质的基本方法和数形结合的思想.
重点
难点
1. 八年级我们学习了一次函数的什么内容?顺序是什么?
概念
图象
性质
2. 还记得如何研究图象和性质的吗?
列表、描点、连线 函数图象 图象的性质;
思考 (1)二次函数的图象是否仍是一条直线呢?若不是,那是什么呢?
(2)系数的符号(正负)与函数图象、性质是否有关呢?
本节课我们将从最简单的二次函数 y=x 开始,逐步深入地讨论一般二次函数的图象和性质.
做一做 画出二次函数 y=x 的图象.
1.列表:在 y = x2 中,自变量 x 可以是任意实数,
列表表示几组对应值;
9
4
1
0
1
4
9
为了便于计算和图象的准确性,我们取的x和y均为整数
x ... -3 -2 -1 0 1 2 3 ...
y = x2 ... ...
还记得如何用描点法画一个函数的图象吗?
点击查看:会变化的二次函数y=ax2的图象
2.描点:根据表中x, y 的数值在坐标平面中描出点(x,y);
3.连线:再用平滑的曲线顺次连接各点,就得到 y=x 的图象.
-3 -2 -1 1 2 3
9
8
7
6
5
4
3
2
1
问题1 观察二次函数的图象,它的形状类似于什么?
投篮
掷铅球
二次函数 y=x 的图象是一条曲线,它的形状类似于投篮时或掷铅球时球在空中所经过的路线,只是这条曲线开口向上. 这条曲线叫做抛物线 y=x .
实际上,二次函数的图象都是抛物线,它们的开口或者向上或者向下.
一般地,二次函数 y=ax +bx+c的图象叫做抛物线 y=ax +bx+c.
-3 -2 -1 1 2 3
9
8
7
6
5
4
3
2
1
抛物线y = x2 与它的对称轴的交点(0,0)叫做抛物线的顶点,它是抛物线y = x2的最低点.
x取值关于原点对称时,y值相同——y轴是抛物线y = x2 的对称轴.
当取更多个点时,二次函数 y=x 的图象如下:
问题2 根据以往学习函数图象特征的经验,说说二次函数 y = x2 的图象有哪些特征
1. y=x2 的图象是一条抛物线;
2. 图象开口向上;
3. 图象关于 y 轴对称;
4. 顶点 (0,0);
5. 图象有最低点.
-3 -2 -1 1 2 3
9
8
7
6
5
4
3
2
1
问题3 观察二次函数 y=x 的图象,y 随 x 如何变化?
从二次函数 y=x 的图象可以看出:
在对称轴的左侧,抛物线从左到右下降→当 x<0 时,y 随 x 的增大而减小;
在对称轴的右侧,抛物线从左到右上升→当 x>0 时,y 随 x 的增大而增大.
-3 -2 -1 1 2 3
9
8
7
6
5
4
3
2
1
例1 在同一直角坐标系中,画出函数 ,y=2x2的图象.
8
4.5
2
0.5
0
0.5
2
x ... -4 -3 -2 -1 0 1 2 3 4 ...
... ...
1.列表:
4.5
8
x ... -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 ...
y=2x2 ... ...
8
4.5
2
0.5
0
0.5
2
4.5
8
2.描点:
3.连线:
-4 -2 2 4
8
6
4
2
问题4 函数 ,y=2x2的图象与函数 y=x2 的图象相比,有什么共同点和不同点?
-4 -2 2 4
8
6
4
2
共同点:开口向上,对称轴是 y 轴,顶点是原点;
不同点:开口大小不同, x2的系数越大,抛物线的开口越小.
二次函数
a的符号
图象
开口方向
顶点坐标
对称轴
增减性
最值
问题5 当a>0时,二次函数 y=ax2 的图象有什么特点?
y=ax2(a≠0)
a>0
向上
(0,0)
y轴
在对称轴的左侧(即x<0),y随x的增大而减小
在对称轴的右侧(即x>0),y随x的增大而增大
当x=0时,
a越大,抛物线的开口越小.
-9
-4
-1
0
-1
-4
-9
x ... -3 -2 -1 0 1 2 3 ...
y = -x2 ... ...
1.列表:
做一做 画出二次函数 y =- x2, ,y=-2x2 的图象.
-8
-4.5
-2
-0.5
0
-0.5
-2
x ... -4 -3 -2 -1 0 1 2 3 4 ...
... ...
-4.5
-8
x ... -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 ...
y=-2x2 ... ...
-8
-4.5
-2
-0.5
0
-0.5
-2
-4.5
-8
2.描点:
3.连线:
y =- x2
问题6 函数 y=-x2, ,y=-2x2的图象之间,有什么共同点和不同点?
共同点:开口向下,对称轴是 y 轴,顶点是原点;
不同点:开口大小不同, x2的系数越小,抛物线的开口越小.
二次函数
a的符号
图象
开口方向
顶点坐标
对称轴
增减性
最值
y=ax2(a≠0)
a<0
向下
(0,0)
y轴
在对称轴的左侧(即x<0),y随x的增大而增大
在对称轴的右侧(即x>0),y随x的增大而减小
问题7 当a<0时,二次函数y=ax2的图象有什么特点?
当x=0时,
a越小,抛物线的开口越小.
问题8 观察右边图象,抛物线y =ax2与y =-ax2 (a>0) 的图象有什么特点?
二次项系数互为相反数时,开口方向相反,开口大小相同,它们关于x轴对称.
|a|越大,抛物线的开口越小.
y =- x2
变式 二次函数y =ax2 与y =-2x2 的形状相同,开口大小一样,开口方向相反,则a=_____.
2
例2 夕夕用软件绘制抛物线 y =4x2 时,将“4”按成了“5”,和原图象相比,发生改变的是( )
A.开口方向 B.开口大小
C.对称轴 D.顶点坐标
B
1.(2024广东)若点(0,y1),(1,y2),(2,y3)都在二次函数y=x2的图象上,则( )
A. y3>y2>y1
B. y2>y1>y3
C. y1>y3>y2
D. y3>y1>y2
A
解:根据题意,得k+2≠0且k2+k-4=2,
解得k1=-3,k2=2,
∵当x<0时,y随x的增大而增大,
∴二次函数的图象的开口向下,即k+2<0,
∴k=-3.
2.已知函数 是二次函数,且当x<0时,y随x的增大而增大.
(1)求k的值;
(2)直接写出顶点坐标和对称轴.
(2)由(1)得y=-x2,
∴顶点坐标为(0,0),对称轴为y轴.
3. 已知二次函数 y = x2,若 x≥m 时,y 最小值为 0,求实数 m 的取值范围.
解:在二次函数 y = x2 中,
当 x = 0 时,y 有最小值,且 y最小值 = 0.
∵ 当 x≥m 时,y最小值 = 0,
∴ m≤0.
4.已知:如图,直线 y=3x+4 与抛物线 y=x2 交于 A、B 两点,求出 A、B 两点的坐标,并求出两交点与原点所围成的三角形的面积
B
解:由题意的
解得 或
∴ 此两函数的交点坐标为A (4,16),B ( 1,1).
∵ 直线 y=3x+4 与 y 轴相交于点 C (0,4),即 CO=4,
∴
∴ S△ABO=S△ACO+S△BOC=10.
二次函数 y=ax2(a≠0) a的符号 a>0 a<0
图象
顶点坐标 对称轴 增减性
最值
1.二次函数y=ax2的图象和性质:
(0,0)
y轴
当x=0时,y最小值=0
当x= 0时,y最大值=0
在对称轴的左侧(即x<0),y随x的增大而减小;在对称轴的右侧(即x>0),y随x的增大而增大
在对称轴的左侧(即x<0),y随x的增大而增大;在对称轴的右侧(即x>0),y随x的增大而减小
y=ax2
a 的符号决
定开口方向
的大小决
定开口大小
a>0,
开口
向上
a<0,
开口
向下
越大,
开口越小
2.二次函数y=ax2的开口方向及大小:
Thanks!
https://www.21cnjy.com/recruitment/home/fine
同课章节目录
