【2025秋人教九上数学情境课堂教学课件】22.1.1 二次函数(主题情境:运动会中的数学问题) 课件(共22张PPT)
文档属性
| 名称 | 【2025秋人教九上数学情境课堂教学课件】22.1.1 二次函数(主题情境:运动会中的数学问题) 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-26 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
人教新版 九下 数学
同步课件
2025年秋人教九上数学情境课堂教学课件
第二十二章 二次函数
22.1 二次函数的图象和性质
22.1.1 二次函数
主题情境·运动会中的数学问题
1.理解并掌握二次函数的概念和一般形式.
2.能根据实际问题中的数量关系列出二次函数解析式.
为了保障学生的身心健康,培养集体协作精神,锻炼坚强的毅力,某校举办了校运动会. 数学小组成员琳琳、婷婷和聪聪在校运动会期间分别发现了一些有趣的数学情境问题.
解:变量为半圆半径 x,两个半圆面积之和 y,
x为自变量,y为因变量.
问题1 如图,是琳琳画出的操场跑道示意图,可看成由两个半圆和一个矩形组成. 设半圆形的半径为 x,两个半圆的面积之和为 y.
(1)问题中有哪些变量?其中哪些是自变量?哪些是因变量?
(2)半径x与面积 y之间的关系该怎么表示?(π取3)
解:y = 3x2 . ①
问题2 婷婷发现在运动会期间,八年级共有n个班参加篮球比赛. 若每两班之间进行一场比赛,比赛的场次数m与球队数n有什么关系?
点拨:每支队伍都要与除自己之外的( n一1)支队伍比赛一次,则共比赛_________场(包含重复比赛场数),由于两支队伍比赛是相互的,应只算一次,所以去掉重复的次数,共比赛_________场.
解:比赛的场次数为
即 ②
问题3 聪聪通过调查发现,由于学生参加校运动会的积极性非常高,所以今年学校增加了每个项目的参赛人数. 已知今年有300名同学参赛,今年比去年的参赛人数增加了t 倍,若按照这样的增长速度,预计两年后的参赛人数 f 与 t 之间有怎样的关系?
点拨:这是一个等比增长的模式,推导出参赛人数与增长倍数之间的关系式,并确定增长倍数的值来进行求解.
解:两年后参赛人数 f = 300(1+t)·(1+t)=300(1+t)2,
即 f = 300t2+600t+300. ③
思考1 针对以上三个式子:
是不是函数这一问题,琳琳和聪聪有了不同的看法,于是婷婷想寻求你的帮助,你认为谁说得对?
是函数,因为对于x(n, t)的每一个确定的值,y(m, f)都有唯一确定的值与其对应.
琳琳
不是函数,因为对于y(m, f)的每一个确定的值,x(n, t)的值不一定是唯一的.
聪聪
琳琳说得对,聪聪对于函数的概念记忆有误.
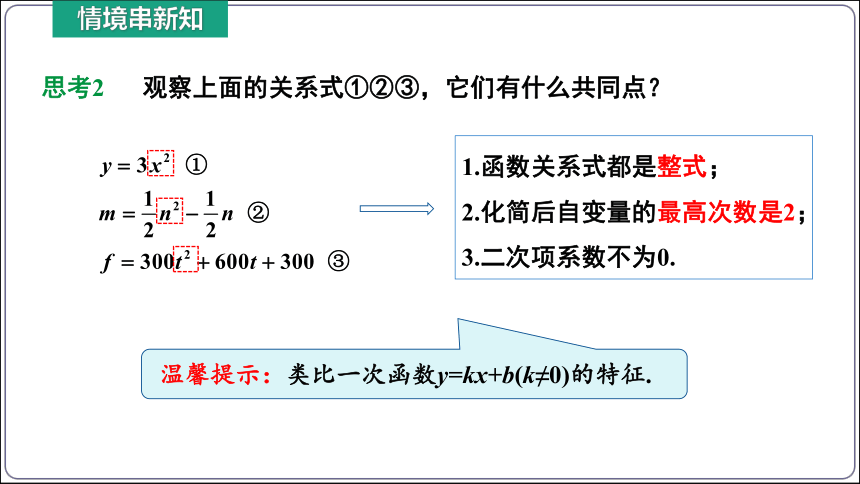
思考2 观察上面的关系式①②③,它们有什么共同点?
温馨提示:类比一次函数y=kx+b(k≠0)的特征.
1.函数关系式都是整式;
2.化简后自变量的最高次数是2;
3.二次项系数不为0.
上述概念中的a为什么不能是0?b和c可否为0?若b和c各自为0或均为0,上述函数的式子可以改写成怎样呢?
当a=0时,可写成y=bx+c;
当b=0时,可写成y=ax +c;
当c=0时,可写成y=ax +bx;
当b=0,c=0时,可写成y=ax .
不是二次函数
温馨提示
(1)等号左边是变量y,右边是关于自变量x的整式;
(2)a,b,c为常数,且a≠0,b,c任意;
(3)等式的右边最高次数为2,可以没有一次项和常数项,但不能没有二次项,即a≠0.
归纳总结
一般地,形如 (a,b,c是常数,a≠0)的函数,叫做二次函数. 其中,x是自变量,a,b,c分别是函数解析式的二次项系数、一次项系数和常数项.
二次项
一次项
常数项
同学们,可以自己举出具体的二次函数吗?
例1 (1)下列函数中,哪些是二次函数?为什么?
① y=ax2+bx+c ② y=3-2x ③y=x2 ④
⑤ ⑥y=x +x +25 ⑦ y=(x+3) -x ⑧y=(2x+1) -6x
不一定是,缺少a≠0的条件.
不是,x的最高次数是3.
不是、化简以后是一次函数
不是,等式右边不是整式
(2) 你能指出上述二次函数的二次项系数,一次项系数和常数项吗?
二次函数关系式 二次项系数 一次项系数 常数项
y=3-2x
y=x2
y=-x -2x
y=(2x+1) -6x
-2
0
3
1
0
0
-1
-2
0
4
-2
1
=-2x +3
=4x -2x+1
温馨提示
确定二次函数的各项系数要注意:
1.先化简成 的形式
2.注意各项系数的符号.
在判断二次函数时,必须满足:
1.函数的关系式是整式;
2.自变量的最高次数是2;
3.二次项系数不等于0.
方法总结
思考3 如何判断一个函数是不是二次函数?
例2 当m 取何值时,函数y=(m2+m)xm2-2m-1+(m-5)x+m2是关于x 的二次函数?并求出二次函数的解析式.
解:由题意,得
①m -2m-3=0,(m-3)(m+1)=0,m = 3或-1
②m(m+1) ≠ 0,m ≠ 0 或m ≠ -1
∴ m = 3.
∴当 m = 3 时,该函数是二次函数,
解析式为:y = (32+3)x32-2×3-1+(3-5)x+32,
即y = 12x2-2x+9.
1.下列函数解析式中,一定为二次函数的是( )
A.
B.
C.
D.
一次函数
当a≠0时为二次函数
函数右边为分式,不是整式,不是二次函数
C
2.下面问题中,y与x满足的函数关系是二次函数的是________.
①等腰三角形ABC的周长为16cm,底边BC长为y cm,腰AB长为x cm,y与x之间的关系;
②底面圆的半径为5cm的圆柱中,侧面积y(cm )与圆柱的高x(cm)的关系;
③某商品每件进价为80元,在某段时间内以每件x元出售,可卖出(100-2x)件.利润y(元)与每件售价x(元)的关系.
③
③y=(x-80)(100-2x)=100x-2x2-8000+160x=-2x2+260x-8000,y是x的二次函数
①y=-2x+16,y是x的一次函数;
②y=2π×5x=10πx,y是x的正比例函数
3.己知函数 y=(a2-3)x2+(a+ )x-7.
(1)若这个函数是一次函数,求出a的值;
解:由题意得, ,解得
(2)若这个函数是二次函数,求出a的取值范围.
解:由题意得, ,解得 且
4.一农民用40 m长的篱笆围成一个一边靠墙的长方形菜园,和墙垂直的一边长为x m,菜园的面积为y m2,求y与x之间的函数关系式,并说出自变量的取值范围. 当x=12 m时,计算菜园的面积.
解:由题意得:y=x(40-2x)
即y=-2x +40x(0<x<20)
当x=12m时,菜园的面积为
y=-2x +40x
=-2×12 +40×12
=192(m )
x
40-2x
一般地,形如 y=ax +bx+c ( a,b,c是常数,a≠ 0 ) 的函数,叫做二次函数. 其中,x是自变量,a,b,c分别是函数解析式的二次项系数、一次项系数和常数项.
1.函数的关系式是整式;
2.自变量的最高次数是2;
3.二次项系数不等于0.
判断方法
定义
二次
函数
Thanks!
https://www.21cnjy.com/recruitment/home/fine
人教新版 九下 数学
同步课件
2025年秋人教九上数学情境课堂教学课件
第二十二章 二次函数
22.1 二次函数的图象和性质
22.1.1 二次函数
主题情境·运动会中的数学问题
1.理解并掌握二次函数的概念和一般形式.
2.能根据实际问题中的数量关系列出二次函数解析式.
为了保障学生的身心健康,培养集体协作精神,锻炼坚强的毅力,某校举办了校运动会. 数学小组成员琳琳、婷婷和聪聪在校运动会期间分别发现了一些有趣的数学情境问题.
解:变量为半圆半径 x,两个半圆面积之和 y,
x为自变量,y为因变量.
问题1 如图,是琳琳画出的操场跑道示意图,可看成由两个半圆和一个矩形组成. 设半圆形的半径为 x,两个半圆的面积之和为 y.
(1)问题中有哪些变量?其中哪些是自变量?哪些是因变量?
(2)半径x与面积 y之间的关系该怎么表示?(π取3)
解:y = 3x2 . ①
问题2 婷婷发现在运动会期间,八年级共有n个班参加篮球比赛. 若每两班之间进行一场比赛,比赛的场次数m与球队数n有什么关系?
点拨:每支队伍都要与除自己之外的( n一1)支队伍比赛一次,则共比赛_________场(包含重复比赛场数),由于两支队伍比赛是相互的,应只算一次,所以去掉重复的次数,共比赛_________场.
解:比赛的场次数为
即 ②
问题3 聪聪通过调查发现,由于学生参加校运动会的积极性非常高,所以今年学校增加了每个项目的参赛人数. 已知今年有300名同学参赛,今年比去年的参赛人数增加了t 倍,若按照这样的增长速度,预计两年后的参赛人数 f 与 t 之间有怎样的关系?
点拨:这是一个等比增长的模式,推导出参赛人数与增长倍数之间的关系式,并确定增长倍数的值来进行求解.
解:两年后参赛人数 f = 300(1+t)·(1+t)=300(1+t)2,
即 f = 300t2+600t+300. ③
思考1 针对以上三个式子:
是不是函数这一问题,琳琳和聪聪有了不同的看法,于是婷婷想寻求你的帮助,你认为谁说得对?
是函数,因为对于x(n, t)的每一个确定的值,y(m, f)都有唯一确定的值与其对应.
琳琳
不是函数,因为对于y(m, f)的每一个确定的值,x(n, t)的值不一定是唯一的.
聪聪
琳琳说得对,聪聪对于函数的概念记忆有误.
思考2 观察上面的关系式①②③,它们有什么共同点?
温馨提示:类比一次函数y=kx+b(k≠0)的特征.
1.函数关系式都是整式;
2.化简后自变量的最高次数是2;
3.二次项系数不为0.
上述概念中的a为什么不能是0?b和c可否为0?若b和c各自为0或均为0,上述函数的式子可以改写成怎样呢?
当a=0时,可写成y=bx+c;
当b=0时,可写成y=ax +c;
当c=0时,可写成y=ax +bx;
当b=0,c=0时,可写成y=ax .
不是二次函数
温馨提示
(1)等号左边是变量y,右边是关于自变量x的整式;
(2)a,b,c为常数,且a≠0,b,c任意;
(3)等式的右边最高次数为2,可以没有一次项和常数项,但不能没有二次项,即a≠0.
归纳总结
一般地,形如 (a,b,c是常数,a≠0)的函数,叫做二次函数. 其中,x是自变量,a,b,c分别是函数解析式的二次项系数、一次项系数和常数项.
二次项
一次项
常数项
同学们,可以自己举出具体的二次函数吗?
例1 (1)下列函数中,哪些是二次函数?为什么?
① y=ax2+bx+c ② y=3-2x ③y=x2 ④
⑤ ⑥y=x +x +25 ⑦ y=(x+3) -x ⑧y=(2x+1) -6x
不一定是,缺少a≠0的条件.
不是,x的最高次数是3.
不是、化简以后是一次函数
不是,等式右边不是整式
(2) 你能指出上述二次函数的二次项系数,一次项系数和常数项吗?
二次函数关系式 二次项系数 一次项系数 常数项
y=3-2x
y=x2
y=-x -2x
y=(2x+1) -6x
-2
0
3
1
0
0
-1
-2
0
4
-2
1
=-2x +3
=4x -2x+1
温馨提示
确定二次函数的各项系数要注意:
1.先化简成 的形式
2.注意各项系数的符号.
在判断二次函数时,必须满足:
1.函数的关系式是整式;
2.自变量的最高次数是2;
3.二次项系数不等于0.
方法总结
思考3 如何判断一个函数是不是二次函数?
例2 当m 取何值时,函数y=(m2+m)xm2-2m-1+(m-5)x+m2是关于x 的二次函数?并求出二次函数的解析式.
解:由题意,得
①m -2m-3=0,(m-3)(m+1)=0,m = 3或-1
②m(m+1) ≠ 0,m ≠ 0 或m ≠ -1
∴ m = 3.
∴当 m = 3 时,该函数是二次函数,
解析式为:y = (32+3)x32-2×3-1+(3-5)x+32,
即y = 12x2-2x+9.
1.下列函数解析式中,一定为二次函数的是( )
A.
B.
C.
D.
一次函数
当a≠0时为二次函数
函数右边为分式,不是整式,不是二次函数
C
2.下面问题中,y与x满足的函数关系是二次函数的是________.
①等腰三角形ABC的周长为16cm,底边BC长为y cm,腰AB长为x cm,y与x之间的关系;
②底面圆的半径为5cm的圆柱中,侧面积y(cm )与圆柱的高x(cm)的关系;
③某商品每件进价为80元,在某段时间内以每件x元出售,可卖出(100-2x)件.利润y(元)与每件售价x(元)的关系.
③
③y=(x-80)(100-2x)=100x-2x2-8000+160x=-2x2+260x-8000,y是x的二次函数
①y=-2x+16,y是x的一次函数;
②y=2π×5x=10πx,y是x的正比例函数
3.己知函数 y=(a2-3)x2+(a+ )x-7.
(1)若这个函数是一次函数,求出a的值;
解:由题意得, ,解得
(2)若这个函数是二次函数,求出a的取值范围.
解:由题意得, ,解得 且
4.一农民用40 m长的篱笆围成一个一边靠墙的长方形菜园,和墙垂直的一边长为x m,菜园的面积为y m2,求y与x之间的函数关系式,并说出自变量的取值范围. 当x=12 m时,计算菜园的面积.
解:由题意得:y=x(40-2x)
即y=-2x +40x(0<x<20)
当x=12m时,菜园的面积为
y=-2x +40x
=-2×12 +40×12
=192(m )
x
40-2x
一般地,形如 y=ax +bx+c ( a,b,c是常数,a≠ 0 ) 的函数,叫做二次函数. 其中,x是自变量,a,b,c分别是函数解析式的二次项系数、一次项系数和常数项.
1.函数的关系式是整式;
2.自变量的最高次数是2;
3.二次项系数不等于0.
判断方法
定义
二次
函数
Thanks!
https://www.21cnjy.com/recruitment/home/fine
同课章节目录
