2024-2025学年山东省淄博市周村区六年级(下)期末数学试卷(五四学制)(含答案)
文档属性
| 名称 | 2024-2025学年山东省淄博市周村区六年级(下)期末数学试卷(五四学制)(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 298.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-24 22:41:45 | ||
图片预览


文档简介
2024-2025学年山东省淄博市周村区六年级(下)期末数学试卷(五四学制)
一、选择题(在每小题给出的四个选项中,只有一个是正确的,请把正确的选项填在题后的括号内,每小题4分,共40分)
1.(4分)已知∠A=50°,则∠A的补角等于( )
A.40° B.50° C.130° D.140°
2.(4分)下列各式运算的结果为a6的是( )
A.a3+a3 B.(a3)3 C.a12÷a2 D.a3 a3
3.(4分)芝麻被称为“八谷之冠”,是世界上最古老的油料作物之一,它作为食品和药物,得到广泛的使用.经测算,一粒芝麻的质量约为0.00000201kg,将100粒芝麻的质量用科学记数法表示约为( )
A.20.1×10﹣3kg B.2.01×10﹣4kg
C.0.201×10﹣5kg D.2.01×10﹣6kg
4.(4分)如图,直线AB,CD相交于点O,OE⊥AB,若∠1=35°,则∠2的度数为( )
A.35° B.45° C.55° D.65°
5.(4分)如图,l1∥l2,等边△ABC的顶点B,C分别在l1,l2上,当∠1=20°时,∠2的大小为( )
A.35° B.40° C.45° D.50°
6.(4分)若(a+1)(a﹣1)=35,则a的值为( )
A.±6 B.±3 C.6 D.3
7.(4分)若m﹣n=3,mn=2,则m2+n2的值为( )
A.5 B.7 C.11 D.13
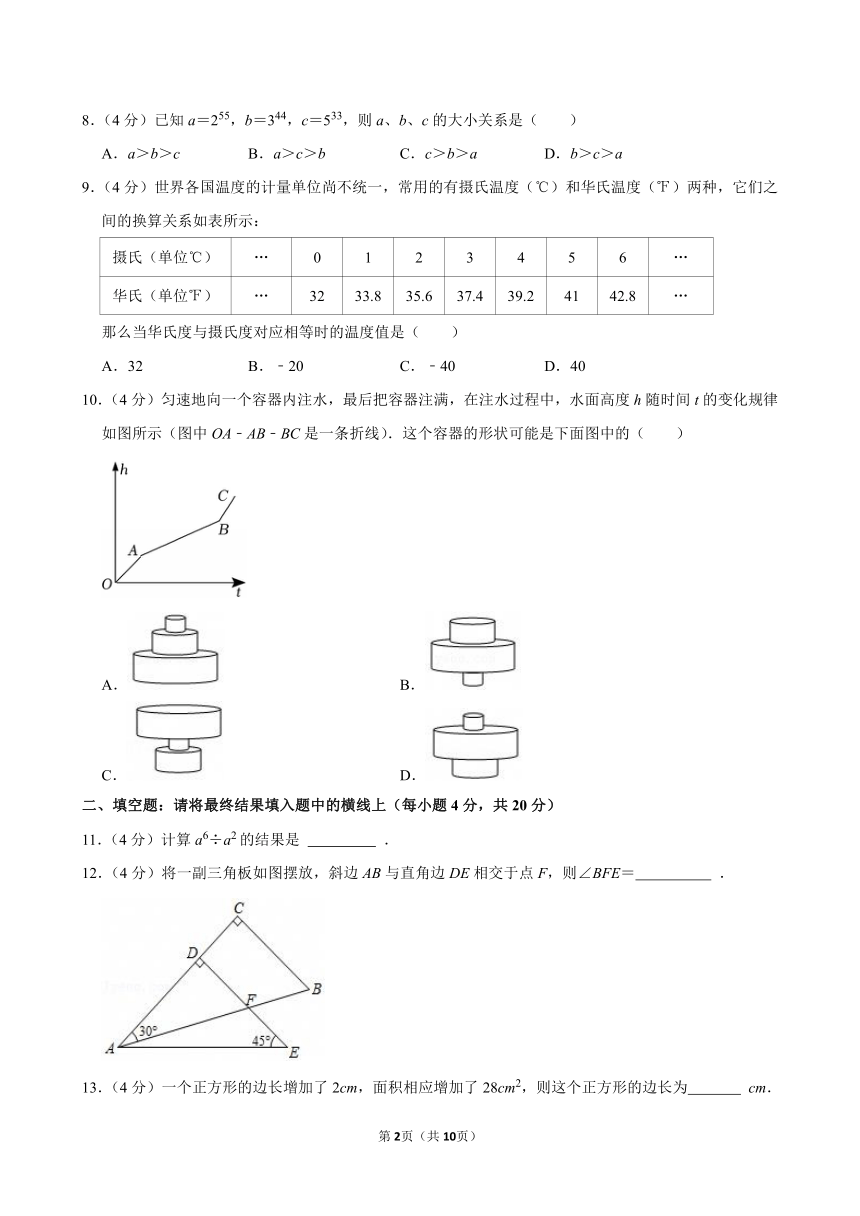
8.(4分)已知a=255,b=344,c=533,则a、b、c的大小关系是( )
A.a>b>c B.a>c>b C.c>b>a D.b>c>a
9.(4分)世界各国温度的计量单位尚不统一,常用的有摄氏温度(℃)和华氏温度(℉)两种,它们之间的换算关系如表所示:
摄氏(单位℃) … 0 1 2 3 4 5 6 …
华氏(单位℉) … 32 33.8 35.6 37.4 39.2 41 42.8 …
那么当华氏度与摄氏度对应相等时的温度值是( )
A.32 B.﹣20 C.﹣40 D.40
10.(4分)匀速地向一个容器内注水,最后把容器注满,在注水过程中,水面高度h随时间t的变化规律如图所示(图中OA﹣AB﹣BC是一条折线).这个容器的形状可能是下面图中的( )
A. B.
C. D.
二、填空题:请将最终结果填入题中的横线上(每小题4分,共20分)
11.(4分)计算a6÷a2的结果是 .
12.(4分)将一副三角板如图摆放,斜边AB与直角边DE相交于点F,则∠BFE= .
13.(4分)一个正方形的边长增加了2cm,面积相应增加了28cm2,则这个正方形的边长为 cm.
14.(4分)小明在一次学科综合实践活动中发现,某品牌鞋子的长度y cm与鞋子的码数x之间满足某种关系,如表给出y与x的一些对应值:
码数x 26 30 34 42
长度y cm 18 20 22 26
根据小明的数据,可以得出该品牌38码鞋子的长度为 cm.
15.(4分)如图,长方形ABCD的周长为8,分别以长方形的一条长和一条宽为边向外作两个正方形,且这两个正方形的面积和为10,则长方形ABCD的面积是 .
三、解答题:要写出必要的文字说明或演算步骤(共90分)
16.(10分)计算:
(1)a3 a2;
(2)1002﹣992.
17.(10分)计算:
(1)(3x2)2 (﹣4y3)÷(6xy);
(2)(x+4)(2x﹣1).
18.(10分)解方程:
(1)5(x+8)﹣5=6(2x﹣7);
(2).
19.(10分)先化简,再求值:
(1)2(6y2﹣3y+2)+2(y﹣1)﹣(2+12y2),其中;
(2)(3x﹣1)2﹣(3x+2)(3x﹣2),其中.
20.(12分)如图,已知∠BAC=90°,DE⊥AC于点H,∠ABD+∠CED=180°.
(1)求证:BD∥EC;
(2)连接BE,若∠BDE=30°,且∠DBE=∠ABE+50°,求∠CEB的度数.
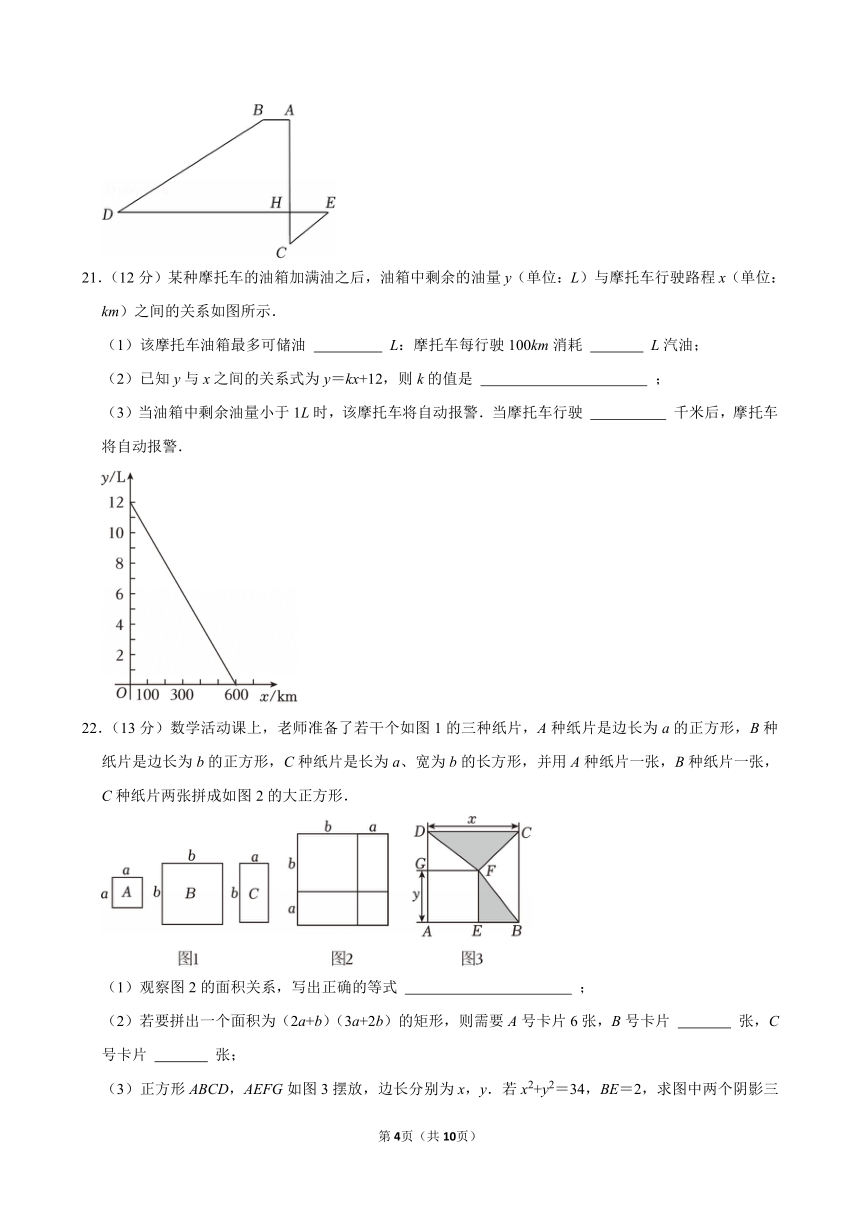
21.(12分)某种摩托车的油箱加满油之后,油箱中剩余的油量y(单位:L)与摩托车行驶路程x(单位:km)之间的关系如图所示.
(1)该摩托车油箱最多可储油 L:摩托车每行驶100km消耗 L汽油;
(2)已知y与x之间的关系式为y=kx+12,则k的值是 ;
(3)当油箱中剩余油量小于1L时,该摩托车将自动报警.当摩托车行驶 千米后,摩托车将自动报警.
22.(13分)数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是长为a、宽为b的长方形,并用A种纸片一张,B种纸片一张,C种纸片两张拼成如图2的大正方形.
(1)观察图2的面积关系,写出正确的等式 ;
(2)若要拼出一个面积为(2a+b)(3a+2b)的矩形,则需要A号卡片6张,B号卡片 张,C号卡片 张;
(3)正方形ABCD,AEFG如图3摆放,边长分别为x,y.若x2+y2=34,BE=2,求图中两个阴影三角形面积和.
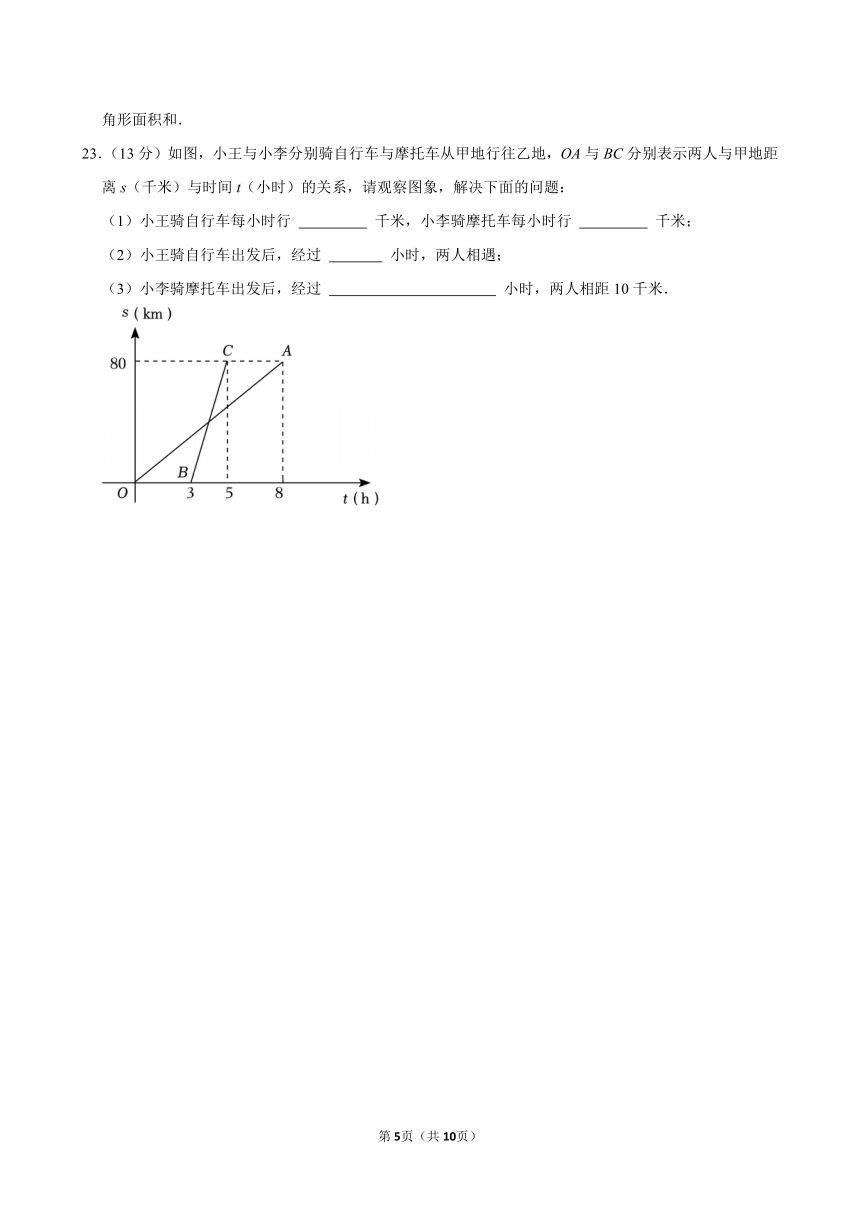
23.(13分)如图,小王与小李分别骑自行车与摩托车从甲地行往乙地,OA与BC分别表示两人与甲地距离s(千米)与时间t(小时)的关系,请观察图象,解决下面的问题:
(1)小王骑自行车每小时行 千米,小李骑摩托车每小时行 千米;
(2)小王骑自行车出发后,经过 小时,两人相遇;
(3)小李骑摩托车出发后,经过 小时,两人相距10千米.
2024-2025学年山东省淄博市周村区六年级(下)期末数学试卷(五四学制)
参考答案与试题解析
一.选择题(共10小题)
题号 1 2 3 4 5 6 7 8 9 10
答案 C D B C B A D C C D
二、填空题:请将最终结果填入题中的横线上(每小题4分,共20分)
11.解:a6÷a2=a6﹣2=a4,
故答案为:a4.
12.解:∵∠DAE=∠E=45°,∠CAF=30°,
∴∠EAF=∠DAE﹣∠DAF=15°,
∴∠BFE=∠FAE+∠E=15°+45°=60°,
故答案为:60°.
13.解:设这个正方形的边长为x cm,
根据题意得:(x+2)2﹣x2=28,
整理得:4x+4=28,
解得:x=6,
则这个正方形的边长为6cm,
故答案为:6
14.解:设y与x的一次函数解析式为y=kx+b,
∵点(26,18),(30,20)在该函数图象上,
∴,
解得,
∴即y与x的函数解析式为,
当x=38时,,
故答案为:24.
15.解:设长方形的长为x,宽为y,由题意得:,
∴x+y=4,
∴(x+y)2=16
∴x2+2xy+y2=16
2xy=16﹣(x2+y2)=16﹣10=6,
∴xy=3,
∴长方形ABCD的面积是3,
故答案为:3.
三、解答题:要写出必要的文字说明或演算步骤(共90分)
16.解:(1)原式=a3+2
=a5;
(2)原式=(100+99)×(100﹣99)
=199×1
=199.
17.解:(1)(3x2)2 (﹣4y3)÷(6xy)
=9x4 (﹣4y3)÷(6xy)
=﹣36x4y3÷(6xy)
=﹣6x3y2;
(2)(x+4)(2x﹣1)
=2x2﹣x+8x﹣4
=2x2+7x﹣4.
18.解:(1)5(x+8)﹣5=6(2x﹣7),
5x+40﹣5=12x﹣42,
5x﹣12x=﹣42﹣40+5,
﹣7x=﹣77,
x=11;
(2),
3(3x﹣1)﹣6=2(5x﹣2),
9x﹣3﹣6=10x﹣4,
9x﹣10x=﹣4+3+6,
﹣x=5,
x=﹣5.
19.解:(1)2(6y2﹣3y+2)+2(y﹣1)﹣(2+12y2)
=12y2﹣6y+4+2y﹣2﹣2﹣12y2
=﹣4y,
当时,
原式=﹣42.
(2)(3x﹣1)2﹣(3x+2)(3x﹣2)
=9x2﹣6x+1﹣9x2+4
=﹣6x+5,
当时,
原式=﹣65=4.
20.(1)证明:∵DE⊥AC,
∴∠AHE=90°,
∵∠BAC=90°,
∴∠BAC=∠AHE=90°,
∴BA∥DE,
∴∠ABD+∠BDE=180°,
∵∠ABD+∠CED=180°,
∴∠BDE=∠CED,
∴BD∥EC;
(2)解:如图,
由(1)可得,∠ABD+∠BDE=180°,
∵∠BDE=30°,
∴∠ABD=180°﹣∠BDE=180°﹣30°=150°,
∵∠DBE=∠ABE+50°,
∴∠ABD=∠ABE+∠DBE=∠ABE+∠ABE+50°=2∠ABE+50°=150°,
∴∠ABE=50°,
∴∠DBE=∠ABE+50°=50°+50°=100°,
∵BD∥EC,
∴∠DBE+∠CEB=180°,
∴∠CEB=180°﹣∠DBE=180°﹣100°=80°.
21.解:(1)该摩托车油箱最多可储油12L,摩托车每行驶100km消耗100=2(L)汽油.
故答案为:12,2.
(2)将坐标(600,0)代入y=kx+12,
得600k+12=0,
解得k.
故答案为:.
(3)当y=1时,得x+12=1,
解得x=550,
∴当摩托车行驶550千米后,摩托车将自动报警.
22.解:(1)由图2知,大正方形的面积为(a+b)2,又可以为a2+2ab+b2,
∴(a+b)2=a2+2ab+b2;
(2)∵(2a+b)(3a+2b)
=6a2+4ab+3ab+2b2
=6a2+7ab+2b2,
∴要拼出一个面积为(2a+b)(3a+2b)的矩形,则需要A号卡片6张,B号卡片2张,C号卡片7张;
(3)由题知:x﹣y=DG=BE=2,x2+y2=34,
则(x﹣y)2=4=x2+y2﹣2xy,则2xy=30,
∴(x+y)2=x2+y2+2xy=34+30=64,
∴x+y=8(负值舍去),
图中阴影部分面积为:.
23.解:(1)小王骑自行车每小时行80÷8=10(千米),小李骑摩托车每小时行80÷(5﹣3)=40(千米).
故答案为:10,40.
(2)当两相遇时,得10t=40(t﹣3),
解得t=4,
∴小王骑自行车出发后,经过4小时,两人相遇.
故答案为:4.
(3)线段OA对应的函数关系式为s=10t,
线段BC对应的函数关系式为s=40(t﹣3)=40t﹣120,
当3≤t≤5时,当两人相距10千米时,得|40t﹣120﹣10t|=10,
解得t或,
当5<t≤8时,当两人相距10千米时,得80﹣10t=10,
解得t=7,
3(小时),3(小时),7﹣3=4(小时),
∴小李骑摩托车出发后,经过小时或小时或4小时,两人相距10千米.
故答案为:或或4.
第1页(共1页)
一、选择题(在每小题给出的四个选项中,只有一个是正确的,请把正确的选项填在题后的括号内,每小题4分,共40分)
1.(4分)已知∠A=50°,则∠A的补角等于( )
A.40° B.50° C.130° D.140°
2.(4分)下列各式运算的结果为a6的是( )
A.a3+a3 B.(a3)3 C.a12÷a2 D.a3 a3
3.(4分)芝麻被称为“八谷之冠”,是世界上最古老的油料作物之一,它作为食品和药物,得到广泛的使用.经测算,一粒芝麻的质量约为0.00000201kg,将100粒芝麻的质量用科学记数法表示约为( )
A.20.1×10﹣3kg B.2.01×10﹣4kg
C.0.201×10﹣5kg D.2.01×10﹣6kg
4.(4分)如图,直线AB,CD相交于点O,OE⊥AB,若∠1=35°,则∠2的度数为( )
A.35° B.45° C.55° D.65°
5.(4分)如图,l1∥l2,等边△ABC的顶点B,C分别在l1,l2上,当∠1=20°时,∠2的大小为( )
A.35° B.40° C.45° D.50°
6.(4分)若(a+1)(a﹣1)=35,则a的值为( )
A.±6 B.±3 C.6 D.3
7.(4分)若m﹣n=3,mn=2,则m2+n2的值为( )
A.5 B.7 C.11 D.13
8.(4分)已知a=255,b=344,c=533,则a、b、c的大小关系是( )
A.a>b>c B.a>c>b C.c>b>a D.b>c>a
9.(4分)世界各国温度的计量单位尚不统一,常用的有摄氏温度(℃)和华氏温度(℉)两种,它们之间的换算关系如表所示:
摄氏(单位℃) … 0 1 2 3 4 5 6 …
华氏(单位℉) … 32 33.8 35.6 37.4 39.2 41 42.8 …
那么当华氏度与摄氏度对应相等时的温度值是( )
A.32 B.﹣20 C.﹣40 D.40
10.(4分)匀速地向一个容器内注水,最后把容器注满,在注水过程中,水面高度h随时间t的变化规律如图所示(图中OA﹣AB﹣BC是一条折线).这个容器的形状可能是下面图中的( )
A. B.
C. D.
二、填空题:请将最终结果填入题中的横线上(每小题4分,共20分)
11.(4分)计算a6÷a2的结果是 .
12.(4分)将一副三角板如图摆放,斜边AB与直角边DE相交于点F,则∠BFE= .
13.(4分)一个正方形的边长增加了2cm,面积相应增加了28cm2,则这个正方形的边长为 cm.
14.(4分)小明在一次学科综合实践活动中发现,某品牌鞋子的长度y cm与鞋子的码数x之间满足某种关系,如表给出y与x的一些对应值:
码数x 26 30 34 42
长度y cm 18 20 22 26
根据小明的数据,可以得出该品牌38码鞋子的长度为 cm.
15.(4分)如图,长方形ABCD的周长为8,分别以长方形的一条长和一条宽为边向外作两个正方形,且这两个正方形的面积和为10,则长方形ABCD的面积是 .
三、解答题:要写出必要的文字说明或演算步骤(共90分)
16.(10分)计算:
(1)a3 a2;
(2)1002﹣992.
17.(10分)计算:
(1)(3x2)2 (﹣4y3)÷(6xy);
(2)(x+4)(2x﹣1).
18.(10分)解方程:
(1)5(x+8)﹣5=6(2x﹣7);
(2).
19.(10分)先化简,再求值:
(1)2(6y2﹣3y+2)+2(y﹣1)﹣(2+12y2),其中;
(2)(3x﹣1)2﹣(3x+2)(3x﹣2),其中.
20.(12分)如图,已知∠BAC=90°,DE⊥AC于点H,∠ABD+∠CED=180°.
(1)求证:BD∥EC;
(2)连接BE,若∠BDE=30°,且∠DBE=∠ABE+50°,求∠CEB的度数.
21.(12分)某种摩托车的油箱加满油之后,油箱中剩余的油量y(单位:L)与摩托车行驶路程x(单位:km)之间的关系如图所示.
(1)该摩托车油箱最多可储油 L:摩托车每行驶100km消耗 L汽油;
(2)已知y与x之间的关系式为y=kx+12,则k的值是 ;
(3)当油箱中剩余油量小于1L时,该摩托车将自动报警.当摩托车行驶 千米后,摩托车将自动报警.
22.(13分)数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是长为a、宽为b的长方形,并用A种纸片一张,B种纸片一张,C种纸片两张拼成如图2的大正方形.
(1)观察图2的面积关系,写出正确的等式 ;
(2)若要拼出一个面积为(2a+b)(3a+2b)的矩形,则需要A号卡片6张,B号卡片 张,C号卡片 张;
(3)正方形ABCD,AEFG如图3摆放,边长分别为x,y.若x2+y2=34,BE=2,求图中两个阴影三角形面积和.
23.(13分)如图,小王与小李分别骑自行车与摩托车从甲地行往乙地,OA与BC分别表示两人与甲地距离s(千米)与时间t(小时)的关系,请观察图象,解决下面的问题:
(1)小王骑自行车每小时行 千米,小李骑摩托车每小时行 千米;
(2)小王骑自行车出发后,经过 小时,两人相遇;
(3)小李骑摩托车出发后,经过 小时,两人相距10千米.
2024-2025学年山东省淄博市周村区六年级(下)期末数学试卷(五四学制)
参考答案与试题解析
一.选择题(共10小题)
题号 1 2 3 4 5 6 7 8 9 10
答案 C D B C B A D C C D
二、填空题:请将最终结果填入题中的横线上(每小题4分,共20分)
11.解:a6÷a2=a6﹣2=a4,
故答案为:a4.
12.解:∵∠DAE=∠E=45°,∠CAF=30°,
∴∠EAF=∠DAE﹣∠DAF=15°,
∴∠BFE=∠FAE+∠E=15°+45°=60°,
故答案为:60°.
13.解:设这个正方形的边长为x cm,
根据题意得:(x+2)2﹣x2=28,
整理得:4x+4=28,
解得:x=6,
则这个正方形的边长为6cm,
故答案为:6
14.解:设y与x的一次函数解析式为y=kx+b,
∵点(26,18),(30,20)在该函数图象上,
∴,
解得,
∴即y与x的函数解析式为,
当x=38时,,
故答案为:24.
15.解:设长方形的长为x,宽为y,由题意得:,
∴x+y=4,
∴(x+y)2=16
∴x2+2xy+y2=16
2xy=16﹣(x2+y2)=16﹣10=6,
∴xy=3,
∴长方形ABCD的面积是3,
故答案为:3.
三、解答题:要写出必要的文字说明或演算步骤(共90分)
16.解:(1)原式=a3+2
=a5;
(2)原式=(100+99)×(100﹣99)
=199×1
=199.
17.解:(1)(3x2)2 (﹣4y3)÷(6xy)
=9x4 (﹣4y3)÷(6xy)
=﹣36x4y3÷(6xy)
=﹣6x3y2;
(2)(x+4)(2x﹣1)
=2x2﹣x+8x﹣4
=2x2+7x﹣4.
18.解:(1)5(x+8)﹣5=6(2x﹣7),
5x+40﹣5=12x﹣42,
5x﹣12x=﹣42﹣40+5,
﹣7x=﹣77,
x=11;
(2),
3(3x﹣1)﹣6=2(5x﹣2),
9x﹣3﹣6=10x﹣4,
9x﹣10x=﹣4+3+6,
﹣x=5,
x=﹣5.
19.解:(1)2(6y2﹣3y+2)+2(y﹣1)﹣(2+12y2)
=12y2﹣6y+4+2y﹣2﹣2﹣12y2
=﹣4y,
当时,
原式=﹣42.
(2)(3x﹣1)2﹣(3x+2)(3x﹣2)
=9x2﹣6x+1﹣9x2+4
=﹣6x+5,
当时,
原式=﹣65=4.
20.(1)证明:∵DE⊥AC,
∴∠AHE=90°,
∵∠BAC=90°,
∴∠BAC=∠AHE=90°,
∴BA∥DE,
∴∠ABD+∠BDE=180°,
∵∠ABD+∠CED=180°,
∴∠BDE=∠CED,
∴BD∥EC;
(2)解:如图,
由(1)可得,∠ABD+∠BDE=180°,
∵∠BDE=30°,
∴∠ABD=180°﹣∠BDE=180°﹣30°=150°,
∵∠DBE=∠ABE+50°,
∴∠ABD=∠ABE+∠DBE=∠ABE+∠ABE+50°=2∠ABE+50°=150°,
∴∠ABE=50°,
∴∠DBE=∠ABE+50°=50°+50°=100°,
∵BD∥EC,
∴∠DBE+∠CEB=180°,
∴∠CEB=180°﹣∠DBE=180°﹣100°=80°.
21.解:(1)该摩托车油箱最多可储油12L,摩托车每行驶100km消耗100=2(L)汽油.
故答案为:12,2.
(2)将坐标(600,0)代入y=kx+12,
得600k+12=0,
解得k.
故答案为:.
(3)当y=1时,得x+12=1,
解得x=550,
∴当摩托车行驶550千米后,摩托车将自动报警.
22.解:(1)由图2知,大正方形的面积为(a+b)2,又可以为a2+2ab+b2,
∴(a+b)2=a2+2ab+b2;
(2)∵(2a+b)(3a+2b)
=6a2+4ab+3ab+2b2
=6a2+7ab+2b2,
∴要拼出一个面积为(2a+b)(3a+2b)的矩形,则需要A号卡片6张,B号卡片2张,C号卡片7张;
(3)由题知:x﹣y=DG=BE=2,x2+y2=34,
则(x﹣y)2=4=x2+y2﹣2xy,则2xy=30,
∴(x+y)2=x2+y2+2xy=34+30=64,
∴x+y=8(负值舍去),
图中阴影部分面积为:.
23.解:(1)小王骑自行车每小时行80÷8=10(千米),小李骑摩托车每小时行80÷(5﹣3)=40(千米).
故答案为:10,40.
(2)当两相遇时,得10t=40(t﹣3),
解得t=4,
∴小王骑自行车出发后,经过4小时,两人相遇.
故答案为:4.
(3)线段OA对应的函数关系式为s=10t,
线段BC对应的函数关系式为s=40(t﹣3)=40t﹣120,
当3≤t≤5时,当两人相距10千米时,得|40t﹣120﹣10t|=10,
解得t或,
当5<t≤8时,当两人相距10千米时,得80﹣10t=10,
解得t=7,
3(小时),3(小时),7﹣3=4(小时),
∴小李骑摩托车出发后,经过小时或小时或4小时,两人相距10千米.
故答案为:或或4.
第1页(共1页)
同课章节目录
