2025-2026学年苏科版八年级数学上册第一次月考测试卷(含答案)
文档属性
| 名称 | 2025-2026学年苏科版八年级数学上册第一次月考测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-25 09:36:44 | ||
图片预览




文档简介
2025-2026学年八年级数学上册第一次月考测试卷
一、选择题(本题共10小题,每小题4分,共40分)
1.下列运算中,错误的有( )
① ;② ;③ ;④ .
A.3个 B.2个 C.1个 D.4个
2.下列命题是假命题的是( )
A.三个角都相等的三角形是等边三角形
B.角平分线上的点到角的两边距离相等
C.等腰三角形的中线就是角平分线
D.到线段两个端点距离相等的点在这条线段的垂直平分线上
3.下列说法正确的是( )
A.近似数精确到 B.近似数精确到百分位
C.近似数万精确到十分位 D.近似数精确到十分位
4.根据相应的条件,不能判断分别给出的两个三角形全等的是( ).
A.如图1,线段与相交于点O,,与
B.如图2,, ABC与
C.如图3,线段相交于点E,已知,与
D.如图4,已知, ABC与
5.已知a,b为实数,且,则的值为( ).
A.10 B.9 C.8 D.7
6.小明同学亲手绘制了一副面积为625的正方形书画作品,准备通过快递邮寄给“红色精神代代传”革命题材书画作品组委会.已知快递站的一种包装袋是长方形,其长、宽之比为3:2,面积为600.请你通过计算帮助小明判断能否在不折叠书画作品的前提下,使用该包装袋进行邮寄?( )
A.能 B.不能,包装袋的长够,宽不够
C.不能,包装袋的长、宽都不够 D.无法判断
7.如图, ABC中,的角平分线和边的垂直平分线交于点,的延长线于点 , 于点. 若,,则的长为( )
A. B. C. D.
8.新规定:对于三个正整数,若其中任意两个数乘积的算术平方根都是整数,则称这三个正整数为“完美组合”,其结果中最小的整数称为“最小算术平方根”,最大的整数称为“最大算术平方根”.例如4,9,16这三个数,,,,其结果都是整数,所以4,9,16三个数称为“完美组合”,其中最小算术平方根是6,最大算术平方根是12.若2,8,18三个数是“完美组合”,则其中最小算术平方根与最大算术平方根的差是( )
A.8 B.16 C.4 D.12
9.如图, ABC为等边三角形, ADE为等腰三角形,其中,,且B,C,D在同一直线上.连接和.则以下结论中正确的个数为( )
①;②为的平分线;③;④.
A.1个 B.2个 C.3个 D.4个
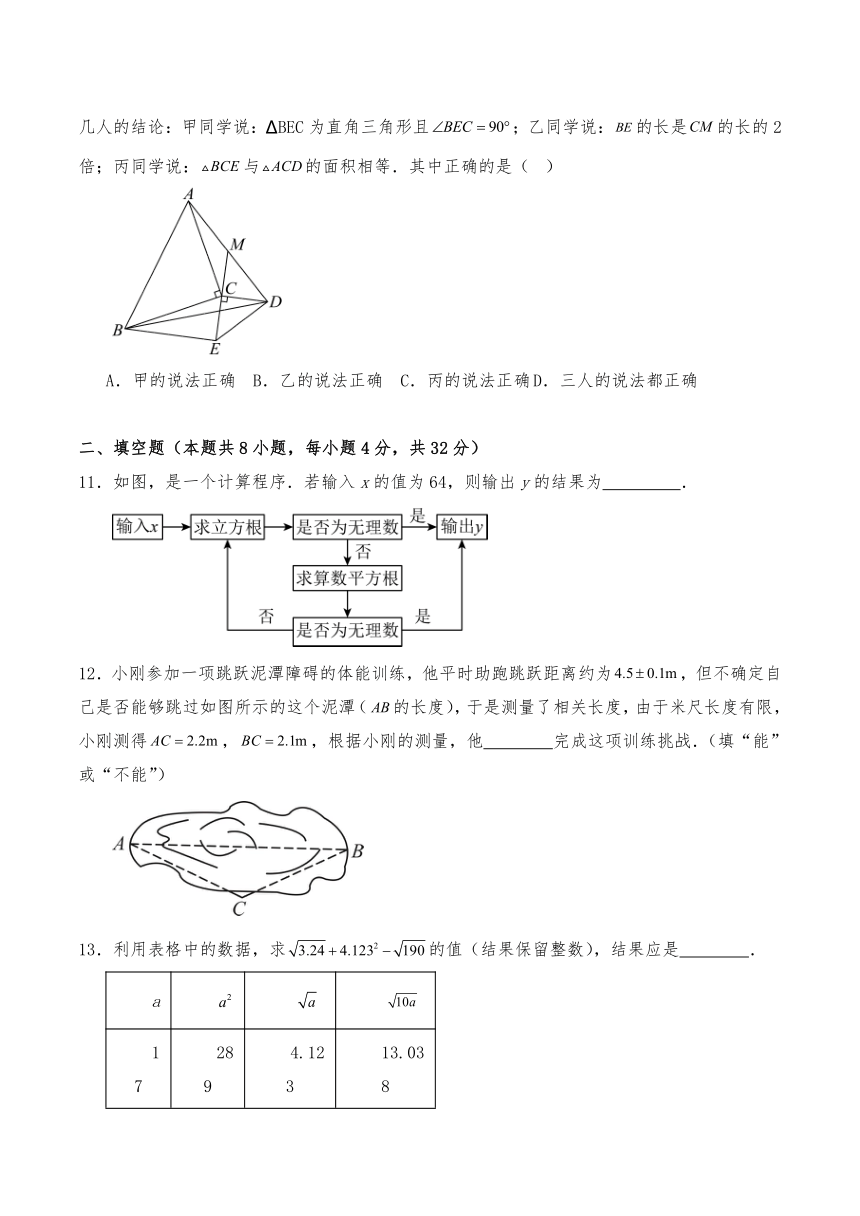
10.如图,在中,,,在 ABC外的Rt DCE中,,,连接,转动Rt DCE使的延长线与线段相交于点M,点M为中点,连接,下列几人的结论:甲同学说: BEC为直角三角形且;乙同学说:的长是的长的2倍;丙同学说:与的面积相等.其中正确的是( )
A.甲的说法正确 B.乙的说法正确 C.丙的说法正确 D.三人的说法都正确
二、填空题(本题共8小题,每小题4分,共32分)
11.如图,是一个计算程序.若输入x的值为64,则输出y的结果为 .
12.小刚参加一项跳跃泥潭障碍的体能训练,他平时助跑跳跃距离约为,但不确定自己是否能够跳过如图所示的这个泥潭(的长度),于是测量了相关长度,由于米尺长度有限,小刚测得,,根据小刚的测量,他 完成这项训练挑战.(填“能”或“不能”)
13.利用表格中的数据,求的值(结果保留整数),结果应是 .
a
17 289 4.123 13.038
18 324 4.243 13.416
19 361 4.359 13.784
14.如果两个数的立方根互为相反数,那么这两个数也互为相反数,即当时,.由此解决下列问题:(1)若,则 ;
(2)若和互为相反数,且的平方根是它本身,则的立方根为 .
15.如图所示的“画图仪”由两根有轨道槽的木条组成,两根木条在点Q处相连并可绕点Q转动.另有长度与相等的两根木条,其中木条的一端S固定在木条上的相应位置,木条可绕点S转动,分别调整点M和点T在相应轨道槽中的位置可改变的大小.若小华同学在某次借助“画图仪”画图时,摆出的位置恰好满足:,则此时 .
16.如图,为 ABC的中线,过点B作交的延长线于点E,点F在线段上且满足,延长交于点G,若,,则线段的长度为 .
17.定义:对于任意实数表示不大于x的最大整数.如:,.若对数65 进行如下运算:①;②;③.这样对数65运算3次后的值就为1.一个正整数总可以经过若干次这样的运算后值为1,则数2025 经过 次这样的运算后值为1.
18.如图,在等腰中,,D为的中点,将两直角边足够长的三角板的直角顶点放在点D处,绕点D任意旋转三角板,使两直角边分别交,于点E,F(点E,F与点A,B,C不重合),连接,下列结论:①,② ADE与有可能全等,③的周长等于 ABC的周长的一半,④四边形的面积等于 ABC的面积的一半.其中正确的结论是 .(填序号)
三、解答题(本题共8小题,共78分。其中:19-20题8分,21-24题每题10分,25-26题每题11分)
19.计算与解方程:
(1);(2);(3).
20.在数学主题乐园,正方形迷宫边长对应正数的平方根分别是和,解出b才能进入,穿过迷宫来到宝藏密室,门锁密码由125的立方根a组成.进入密室后,需解出关于x的方程,才能兑换奖励.(1)求a, b, x的值;(2)将奖励存入边长为的正方体盒子,若盒子体积比大k,求的算术平方根.
21.【阅读材料】对于实数,我们规定:用表示的整数部分.例如:因为,所以的整数部分为1,即;因为,所以的整数部分为2,即.
【应用】(1)填空:_______.(2)若,求出满足题意的所有的整数值.
【拓展】(3)如果我们将正实数的整数部分进行开方,得出算术平方根为1次运算,将上述运算一直进行下去,直到结果为1时停止运算.例如:,3的算术平方根为;,1的算术平方根为1,此时运算停止,共进行2次运算.求对实数经过几次运算之后的结果是1?
22.探索新知:如图①,是 ABC的角平分线,与之间有怎样的关系呢?过点D作,垂足分别为E,F,过点A作,垂足为H.
平分;
∴S ABD= AB DE= BD AH,
即.
新知应用:(1)如图②,是 ABC的角平分线,若,则_________;
(2)如图②,是 ABC的角平分线,若,则_________;
(3)如图③,平分,平分,若,,求四边形AEFD的值。(用含m的式子表示).
23.项目式学习活动主题:估算纸的长与宽
【知识储备】(1)如图1,把两个边长为1的小正方形沿对角线剪开,所得的4个直角三角形拼成一个面积为2的大正方形,则大正方形的边长为 .
一般结论:正方形的对角线与边长的比是 .
【项目素材】如图2,按照国际标准,A系列纸为长方形(长宽比相同),其中纸的面积为.
将纸沿长边对折、裁开,便成两张纸;将纸沿长边对折、裁开,便成两张纸;将纸沿长边对折、裁开,便成两张纸;......,将纸沿长边对折、裁开,便成两张纸.
(2)【任务探究】任务一:纸面积是纸面积的 倍,纸周长是纸周长的 倍;
(3) 任务二:将一张纸按如图3所示进行两次折叠(折痕分别是AB和AE),观察发现点B恰好和点C重合,求纸的长与宽之比.
(4) 任务三:根据上述结论,估算纸的长和宽分别是多少毫米(结果取整数).
(参考数据:,,,,,,,)
24.折叠可以解决很多问题.我们知道:在一个三角形中,等边所对的角相等,那么不相等的边所对的角之间的大小关系是怎样呢
【问题情境】如图1,在 ABC中,,怎样判断与的大小关系呢
解答:将边折叠,使落在边上,点C的对应点为,折痕与交于点D.
由折叠可得.又,;
结论:在三角形中,大边对大角;反之,大角对大边.
(1)若,,求的度数;
(2)若,判断,与之间的数量关系,并说明理由;
【变式探究】(3)如图2,在中,,,是 ABC的角平分线.设,,求的长(用含a,b的代数式表示);
【思维拓展】(4)在 ABC中,,,D是边上的动点,连接,将沿折叠,得到,且点E在直线的下方,与边交于点M.继续将向下折叠,使边与重合,折痕为(F在边上),连接.若是等腰三角形,请直接写出的度数.
25.【模型呈现】“数学区别于其它学科最主要的特征是抽象与推理”.“一线三等角”模型是几何世界中常见的模型之一,只要细心观察,你就可以从中找到全等三角形.
(1)【模型理解】如图1,已知,点C在线段DE上,,若,则与的数量关系为 ,,与的数量关系为 ;
(2)【拓展延伸】在中,,分别以、为腰,在左侧作等腰直角三角形,在右侧作等腰直角三角形,其中,,
① 如图2,连接,当交线段的延长线于点M时,求证:;
② 如图3,连接,当交线段于点M,且时,求的长.
26.【问题提出】(1)如图①,在 ABC中,若,,AD是边上的中线,求的取值范围.小明的做法如下:如图①,延长至点,使,连接,则,依据的判定方法是___,由三角形的三边关系可知的取值范围为___;
(2)如图②,,,,点为的中点,试说明:;
【问题解决】(3)如图③,四边形是某公园的一片玫瑰园,对角线是中间的一条通道,现正值玫瑰盛开的旺季,为方便游客观赏,要沿对角线铺设一条小路,在两条小路的交点处修建一座观景塔(观景塔大小忽略不计),在边的中点处设置一个出入口,再沿铺设一条小路将游客分流,采购部需要知道与之间的数量关系购买原材料.按照设计要求,,,请你帮采购部探究线段与之间的数量关系(小路宽度忽略不计).
参考答案
一、选择题
1.A
【详解】解:①,错误;
②,原式错误;
③,正确;
④,原式错误;
综上,错误的有①②④,共3个,故选:A.
2.C
【详解】A.三个角都相等的三角形是等边三角形,符合等边三角形的判定定理,为真命题.
B.角平分线上的点到角的两边距离相等,符合角平分线的基本性质,为真命题.
C.等腰三角形的中线是否为角平分线需具体分析.等腰三角形底边上的中线、高线、顶角平分线三线合一,但若中线为腰上的中线,则不一定为角平分线.题干未明确“中线”的位置,表述不严谨,存在反例,故为假命题.
D.到线段两端点距离相等的点在线段的垂直平分线上,符合垂直平分线的判定定理,为真命题.故选:C.
3.B
【详解】解:A、近似数精确到,故本选项错误,不符合题意;
B、近似数精确到百分位,故本选项正确,符合题意;
C、近似数万精确到千位,故本选项错误,不符合题意;
D、近似数精确到百位,故本选项错误,不符合题意;故选:B
4.C
【详解】解:A.在图1中,由,根据“”证明,可判断A不符合题意;
B.在图2中,由,根据“”证明,可判断B不符合题意;
C.在图3中,不符合全等三角形判定定理的条件,因此不能判断与全等,可判断C符合题意;
D.在图4中,由,根据“”证明,可判断D不符合题意.故选:C.
5.D
【详解】解:∵,,,
∴,,∴,故选:D.
6.B
【详解】(1)解:面积为的正方形书画作品的边长是.
包装袋的长、宽之比为,设长方形包装袋的长为,宽为,
由题意得,即,(负值舍去),长方形包装袋的长为,宽为;
,不能,包装袋的长够,宽不够.故选B.
7.B
【详解】解:连接
∵是的平分线 ,∴,∵,,∴,
在和中 ,,∴,∴,,
∵是的垂直平分线,∴,
在和中 ,,∴,∴,
∵,,∴,∴,故选:.
8.A
【详解】解:∵,,,
∴最小算术平方根是4,最大算术平方根是12,
∴最小算术平方根与最大算术平方根的差是.故答案为:A.
9.C
【详解】解:∵ ABC为等边三角形,,
∵,,
∵四边形中,,
.故结论①正确;
如图,过E点作的延长线于F点,作于G点.则,
,,,
又,,,∴为的平分线.故结论②正确;
, 平分,∴垂直平分,∴.故结论③正确;
,而, ,.故结论④不正确;
综上,正确的结论有3个.故选:C.
10.D
【详解】解:延长,过点A作于点F,如图所示:则,
∵,∴,∴,∵点M为的中点,∴,
∵,∴,∴,,,
∵,∴,∵,∴,
∵,∴,∵,∴,
∴,,,
∴ BEC为直角三角形且,故甲说法正确;
∵,,∴,故乙说法正确;
∵,∴,
∵,∴,故丙说法正确;综上分析可知:三个人的说法都正确.故选:D.
二、填空题
11.
【详解】解:输入,
第一步:求64的立方根,,是有理数,不输出;
第二步:求4的算术平方根,,2是有理数,不输出;
第三步:求2的立方根,是无理数,输出y.故答案为:.
12.能
【详解】解:由题意可知,,
∴小刚能完成这项训练挑战.故答案为:能.
13.5
【详解】解:∵,∴,∵,∴,
∵,∴,故答案为:5.
14. 2.65
【详解】解:(1)根据题意可知与互为相反数,故,故答案为:2.65;
(2)根据题意,得,解得.
的平方根是它本身,,解得.
,故的立方根为,故答案为:.
15.
【详解】解:由题意可得,为等边三角形,
,,
,,,,故答案为:.
16.
【详解】解:∵为的中线,∴,∵,∴,
又∵,∴,∴,∵,∴,
又∵,∴,∴,
∴,∴;故答案为:.
17.4
【详解】解:①∵,∴.
②∵,∴.
③∵,∴.
④∵,∴.故答案为:4.
18.①②④
【详解】解:如图,连接,∵在等腰中,,D为的中点,
∴,,,
∵,∴,
∴,∴,∴,,故①正确;
∴的周长
∵ ABC的周长
∵不一定相等,∴的周长不一定等于 ABC的周长的一半,故③错误;
∵∴是直角三角形
∵,点E,F与点A,B,C不重合;∴;∴当时,
∵是等腰直角三角形;∴;∴,故②正确;
∵;∴,∴,④正确;
综上所述,其中正确的结论是①②④.故答案为:①②④.
三、解答题
19.(1)解:,∴,∴.
(2)解:∵,∴,∴或,∴或;
(3)原式.
(4)原式.
20.(1)解:∵正方形迷宫边长对应正数的平方根分别是和,
∴,∴,
∵a是125的立方根,∴,∴方程变形为,解得;
(2)解:根据题意,得,
∴的算术平方根为.
21.解:(1)因为,
∴,即,∴.
(2)因为,,,所以,
所以的整数值为4或5或6或7或8.
(3)因为,所以,即,
故第1次运算:,11的算术平方根为;
因为,所以,即,
第2次运算:,的算术平方根为;
因为,所以,即,
第3次运算:,1的算术平方根为1.故对实数经过3次运算之后的结果是1.
22.(1)解:过点D作,垂足分别为E,F,过点A作,垂足为H
由探索新知,是 ABC的角平分线时,,
∵,,∴.设,,
∴,∴.
(2)解:过点D作,垂足分别为E,F,过点A作,垂足为H
由探索新知可知,对于 ABC,是角平分线时:
,;,
∵;∴.∵,∴.故答案为;(
(3)∵平分,∴点D到,的距离相等,∴,
∵,∴,,同理平分,
∴,∴,,
连接,过点F作,,分别垂直于,,,
∵平分,平分,∴,,∴
∴平分,∴点F到,,三边的距离相等,
∴,
∵;∴,,,
∴.故答案为.
23.解:(1)两个边长为1的小正方形 ,合成一个大正方形面积为2,
大正方形的边长为; 正方形的对角线与边长的比是,故答案为:;
(2)根据图2的面积关系发现:纸面积是纸面积的2倍,纸周长是纸周长2倍;
故答案为:2,2;
(3)解:由折叠的性质可知,由(1)可知在正方形中,
,即A4纸的长宽之比为;
(4)解:由(3)可知:纸的长与宽之比是
设纸的宽为,则长为,纸的面积为,,
,,
;故纸的宽约为,长约为.
24.解:(1)∵在 ABC中,,,∴,
∵将沿折叠,点C落在上,点C的对应点为,如图1所示:∴,
∵,∴,∴;
(2),与之间的数量关系是:,理由如下:
将边折叠,使落在边上,点C的对应点为,折痕与交于点D,如图2所示:
根据折叠的性质得:,,,∵,∴,
又∵,∴,
∴,∴,∴,∴;
(3)将边折叠,使落在边上,点C的对应点为,折痕与交于点D,如图3所示:
根据折叠的性质得:,,,
在中,,,∴,∴,
∵,∴,∴,
∴,∴,∵,,∴,
在中,,∴,∴;
(4)在 ABC中,,,∴,如图4所示:
设,∴,∴,
根据折叠的性质得:,,
∴,
∵将向下折叠,使边与重合,折痕为(F在边上),∴,
∴,∴,
在中,,,,
当是等腰三角形时,有以下三种情况:
当时,则,∴,解得:,∴;
当时,则,∴,解得:,∴;
当时,则,∴,解得:,∴,
综上所述:当是等腰三角形时,的度数为或或.
25.(1)解:,
,
又,, ,
由.故答案为:;.
(2)解:①作交直线于E,则,
,,
∵,∴,∴,
又∵,,∴,
∴,∴,∴,
又∵,,∴,∴.
②作交直线于E,则,
由①得,,,,,,
∴ ×BP×AC=3× ×AM×QE,,设,则,
∴CP=BP -BC=3x-1,,
∴3x-1=1-2x,解得:,∴BP=3x=.
26.(1)解:延长到点E.使,连接,
∵是的中线,∴,又,
∴,∴,
∵在中,,∴,
∵,∴,∴;
(2)证明:延长至G,使,连接,则
∵点D为的中点,∴,
在和中,∴,∴,,
∵,∴,∵,∴,
∴,
在和中,∴,∴.
(3)解:如图,延长到G,使得,连接,延长到H,使得,连接,
∵点F是边的中点,∴,∵,∴,
∴,,∴,∴,
∵,∴,
∵,∴.∴,,
∵,∴,∴,∴.
一、选择题(本题共10小题,每小题4分,共40分)
1.下列运算中,错误的有( )
① ;② ;③ ;④ .
A.3个 B.2个 C.1个 D.4个
2.下列命题是假命题的是( )
A.三个角都相等的三角形是等边三角形
B.角平分线上的点到角的两边距离相等
C.等腰三角形的中线就是角平分线
D.到线段两个端点距离相等的点在这条线段的垂直平分线上
3.下列说法正确的是( )
A.近似数精确到 B.近似数精确到百分位
C.近似数万精确到十分位 D.近似数精确到十分位
4.根据相应的条件,不能判断分别给出的两个三角形全等的是( ).
A.如图1,线段与相交于点O,,与
B.如图2,, ABC与
C.如图3,线段相交于点E,已知,与
D.如图4,已知, ABC与
5.已知a,b为实数,且,则的值为( ).
A.10 B.9 C.8 D.7
6.小明同学亲手绘制了一副面积为625的正方形书画作品,准备通过快递邮寄给“红色精神代代传”革命题材书画作品组委会.已知快递站的一种包装袋是长方形,其长、宽之比为3:2,面积为600.请你通过计算帮助小明判断能否在不折叠书画作品的前提下,使用该包装袋进行邮寄?( )
A.能 B.不能,包装袋的长够,宽不够
C.不能,包装袋的长、宽都不够 D.无法判断
7.如图, ABC中,的角平分线和边的垂直平分线交于点,的延长线于点 , 于点. 若,,则的长为( )
A. B. C. D.
8.新规定:对于三个正整数,若其中任意两个数乘积的算术平方根都是整数,则称这三个正整数为“完美组合”,其结果中最小的整数称为“最小算术平方根”,最大的整数称为“最大算术平方根”.例如4,9,16这三个数,,,,其结果都是整数,所以4,9,16三个数称为“完美组合”,其中最小算术平方根是6,最大算术平方根是12.若2,8,18三个数是“完美组合”,则其中最小算术平方根与最大算术平方根的差是( )
A.8 B.16 C.4 D.12
9.如图, ABC为等边三角形, ADE为等腰三角形,其中,,且B,C,D在同一直线上.连接和.则以下结论中正确的个数为( )
①;②为的平分线;③;④.
A.1个 B.2个 C.3个 D.4个
10.如图,在中,,,在 ABC外的Rt DCE中,,,连接,转动Rt DCE使的延长线与线段相交于点M,点M为中点,连接,下列几人的结论:甲同学说: BEC为直角三角形且;乙同学说:的长是的长的2倍;丙同学说:与的面积相等.其中正确的是( )
A.甲的说法正确 B.乙的说法正确 C.丙的说法正确 D.三人的说法都正确
二、填空题(本题共8小题,每小题4分,共32分)
11.如图,是一个计算程序.若输入x的值为64,则输出y的结果为 .
12.小刚参加一项跳跃泥潭障碍的体能训练,他平时助跑跳跃距离约为,但不确定自己是否能够跳过如图所示的这个泥潭(的长度),于是测量了相关长度,由于米尺长度有限,小刚测得,,根据小刚的测量,他 完成这项训练挑战.(填“能”或“不能”)
13.利用表格中的数据,求的值(结果保留整数),结果应是 .
a
17 289 4.123 13.038
18 324 4.243 13.416
19 361 4.359 13.784
14.如果两个数的立方根互为相反数,那么这两个数也互为相反数,即当时,.由此解决下列问题:(1)若,则 ;
(2)若和互为相反数,且的平方根是它本身,则的立方根为 .
15.如图所示的“画图仪”由两根有轨道槽的木条组成,两根木条在点Q处相连并可绕点Q转动.另有长度与相等的两根木条,其中木条的一端S固定在木条上的相应位置,木条可绕点S转动,分别调整点M和点T在相应轨道槽中的位置可改变的大小.若小华同学在某次借助“画图仪”画图时,摆出的位置恰好满足:,则此时 .
16.如图,为 ABC的中线,过点B作交的延长线于点E,点F在线段上且满足,延长交于点G,若,,则线段的长度为 .
17.定义:对于任意实数表示不大于x的最大整数.如:,.若对数65 进行如下运算:①;②;③.这样对数65运算3次后的值就为1.一个正整数总可以经过若干次这样的运算后值为1,则数2025 经过 次这样的运算后值为1.
18.如图,在等腰中,,D为的中点,将两直角边足够长的三角板的直角顶点放在点D处,绕点D任意旋转三角板,使两直角边分别交,于点E,F(点E,F与点A,B,C不重合),连接,下列结论:①,② ADE与有可能全等,③的周长等于 ABC的周长的一半,④四边形的面积等于 ABC的面积的一半.其中正确的结论是 .(填序号)
三、解答题(本题共8小题,共78分。其中:19-20题8分,21-24题每题10分,25-26题每题11分)
19.计算与解方程:
(1);(2);(3).
20.在数学主题乐园,正方形迷宫边长对应正数的平方根分别是和,解出b才能进入,穿过迷宫来到宝藏密室,门锁密码由125的立方根a组成.进入密室后,需解出关于x的方程,才能兑换奖励.(1)求a, b, x的值;(2)将奖励存入边长为的正方体盒子,若盒子体积比大k,求的算术平方根.
21.【阅读材料】对于实数,我们规定:用表示的整数部分.例如:因为,所以的整数部分为1,即;因为,所以的整数部分为2,即.
【应用】(1)填空:_______.(2)若,求出满足题意的所有的整数值.
【拓展】(3)如果我们将正实数的整数部分进行开方,得出算术平方根为1次运算,将上述运算一直进行下去,直到结果为1时停止运算.例如:,3的算术平方根为;,1的算术平方根为1,此时运算停止,共进行2次运算.求对实数经过几次运算之后的结果是1?
22.探索新知:如图①,是 ABC的角平分线,与之间有怎样的关系呢?过点D作,垂足分别为E,F,过点A作,垂足为H.
平分;
∴S ABD= AB DE= BD AH,
即.
新知应用:(1)如图②,是 ABC的角平分线,若,则_________;
(2)如图②,是 ABC的角平分线,若,则_________;
(3)如图③,平分,平分,若,,求四边形AEFD的值。(用含m的式子表示).
23.项目式学习活动主题:估算纸的长与宽
【知识储备】(1)如图1,把两个边长为1的小正方形沿对角线剪开,所得的4个直角三角形拼成一个面积为2的大正方形,则大正方形的边长为 .
一般结论:正方形的对角线与边长的比是 .
【项目素材】如图2,按照国际标准,A系列纸为长方形(长宽比相同),其中纸的面积为.
将纸沿长边对折、裁开,便成两张纸;将纸沿长边对折、裁开,便成两张纸;将纸沿长边对折、裁开,便成两张纸;......,将纸沿长边对折、裁开,便成两张纸.
(2)【任务探究】任务一:纸面积是纸面积的 倍,纸周长是纸周长的 倍;
(3) 任务二:将一张纸按如图3所示进行两次折叠(折痕分别是AB和AE),观察发现点B恰好和点C重合,求纸的长与宽之比.
(4) 任务三:根据上述结论,估算纸的长和宽分别是多少毫米(结果取整数).
(参考数据:,,,,,,,)
24.折叠可以解决很多问题.我们知道:在一个三角形中,等边所对的角相等,那么不相等的边所对的角之间的大小关系是怎样呢
【问题情境】如图1,在 ABC中,,怎样判断与的大小关系呢
解答:将边折叠,使落在边上,点C的对应点为,折痕与交于点D.
由折叠可得.又,;
结论:在三角形中,大边对大角;反之,大角对大边.
(1)若,,求的度数;
(2)若,判断,与之间的数量关系,并说明理由;
【变式探究】(3)如图2,在中,,,是 ABC的角平分线.设,,求的长(用含a,b的代数式表示);
【思维拓展】(4)在 ABC中,,,D是边上的动点,连接,将沿折叠,得到,且点E在直线的下方,与边交于点M.继续将向下折叠,使边与重合,折痕为(F在边上),连接.若是等腰三角形,请直接写出的度数.
25.【模型呈现】“数学区别于其它学科最主要的特征是抽象与推理”.“一线三等角”模型是几何世界中常见的模型之一,只要细心观察,你就可以从中找到全等三角形.
(1)【模型理解】如图1,已知,点C在线段DE上,,若,则与的数量关系为 ,,与的数量关系为 ;
(2)【拓展延伸】在中,,分别以、为腰,在左侧作等腰直角三角形,在右侧作等腰直角三角形,其中,,
① 如图2,连接,当交线段的延长线于点M时,求证:;
② 如图3,连接,当交线段于点M,且时,求的长.
26.【问题提出】(1)如图①,在 ABC中,若,,AD是边上的中线,求的取值范围.小明的做法如下:如图①,延长至点,使,连接,则,依据的判定方法是___,由三角形的三边关系可知的取值范围为___;
(2)如图②,,,,点为的中点,试说明:;
【问题解决】(3)如图③,四边形是某公园的一片玫瑰园,对角线是中间的一条通道,现正值玫瑰盛开的旺季,为方便游客观赏,要沿对角线铺设一条小路,在两条小路的交点处修建一座观景塔(观景塔大小忽略不计),在边的中点处设置一个出入口,再沿铺设一条小路将游客分流,采购部需要知道与之间的数量关系购买原材料.按照设计要求,,,请你帮采购部探究线段与之间的数量关系(小路宽度忽略不计).
参考答案
一、选择题
1.A
【详解】解:①,错误;
②,原式错误;
③,正确;
④,原式错误;
综上,错误的有①②④,共3个,故选:A.
2.C
【详解】A.三个角都相等的三角形是等边三角形,符合等边三角形的判定定理,为真命题.
B.角平分线上的点到角的两边距离相等,符合角平分线的基本性质,为真命题.
C.等腰三角形的中线是否为角平分线需具体分析.等腰三角形底边上的中线、高线、顶角平分线三线合一,但若中线为腰上的中线,则不一定为角平分线.题干未明确“中线”的位置,表述不严谨,存在反例,故为假命题.
D.到线段两端点距离相等的点在线段的垂直平分线上,符合垂直平分线的判定定理,为真命题.故选:C.
3.B
【详解】解:A、近似数精确到,故本选项错误,不符合题意;
B、近似数精确到百分位,故本选项正确,符合题意;
C、近似数万精确到千位,故本选项错误,不符合题意;
D、近似数精确到百位,故本选项错误,不符合题意;故选:B
4.C
【详解】解:A.在图1中,由,根据“”证明,可判断A不符合题意;
B.在图2中,由,根据“”证明,可判断B不符合题意;
C.在图3中,不符合全等三角形判定定理的条件,因此不能判断与全等,可判断C符合题意;
D.在图4中,由,根据“”证明,可判断D不符合题意.故选:C.
5.D
【详解】解:∵,,,
∴,,∴,故选:D.
6.B
【详解】(1)解:面积为的正方形书画作品的边长是.
包装袋的长、宽之比为,设长方形包装袋的长为,宽为,
由题意得,即,(负值舍去),长方形包装袋的长为,宽为;
,不能,包装袋的长够,宽不够.故选B.
7.B
【详解】解:连接
∵是的平分线 ,∴,∵,,∴,
在和中 ,,∴,∴,,
∵是的垂直平分线,∴,
在和中 ,,∴,∴,
∵,,∴,∴,故选:.
8.A
【详解】解:∵,,,
∴最小算术平方根是4,最大算术平方根是12,
∴最小算术平方根与最大算术平方根的差是.故答案为:A.
9.C
【详解】解:∵ ABC为等边三角形,,
∵,,
∵四边形中,,
.故结论①正确;
如图,过E点作的延长线于F点,作于G点.则,
,,,
又,,,∴为的平分线.故结论②正确;
, 平分,∴垂直平分,∴.故结论③正确;
,而, ,.故结论④不正确;
综上,正确的结论有3个.故选:C.
10.D
【详解】解:延长,过点A作于点F,如图所示:则,
∵,∴,∴,∵点M为的中点,∴,
∵,∴,∴,,,
∵,∴,∵,∴,
∵,∴,∵,∴,
∴,,,
∴ BEC为直角三角形且,故甲说法正确;
∵,,∴,故乙说法正确;
∵,∴,
∵,∴,故丙说法正确;综上分析可知:三个人的说法都正确.故选:D.
二、填空题
11.
【详解】解:输入,
第一步:求64的立方根,,是有理数,不输出;
第二步:求4的算术平方根,,2是有理数,不输出;
第三步:求2的立方根,是无理数,输出y.故答案为:.
12.能
【详解】解:由题意可知,,
∴小刚能完成这项训练挑战.故答案为:能.
13.5
【详解】解:∵,∴,∵,∴,
∵,∴,故答案为:5.
14. 2.65
【详解】解:(1)根据题意可知与互为相反数,故,故答案为:2.65;
(2)根据题意,得,解得.
的平方根是它本身,,解得.
,故的立方根为,故答案为:.
15.
【详解】解:由题意可得,为等边三角形,
,,
,,,,故答案为:.
16.
【详解】解:∵为的中线,∴,∵,∴,
又∵,∴,∴,∵,∴,
又∵,∴,∴,
∴,∴;故答案为:.
17.4
【详解】解:①∵,∴.
②∵,∴.
③∵,∴.
④∵,∴.故答案为:4.
18.①②④
【详解】解:如图,连接,∵在等腰中,,D为的中点,
∴,,,
∵,∴,
∴,∴,∴,,故①正确;
∴的周长
∵ ABC的周长
∵不一定相等,∴的周长不一定等于 ABC的周长的一半,故③错误;
∵∴是直角三角形
∵,点E,F与点A,B,C不重合;∴;∴当时,
∵是等腰直角三角形;∴;∴,故②正确;
∵;∴,∴,④正确;
综上所述,其中正确的结论是①②④.故答案为:①②④.
三、解答题
19.(1)解:,∴,∴.
(2)解:∵,∴,∴或,∴或;
(3)原式.
(4)原式.
20.(1)解:∵正方形迷宫边长对应正数的平方根分别是和,
∴,∴,
∵a是125的立方根,∴,∴方程变形为,解得;
(2)解:根据题意,得,
∴的算术平方根为.
21.解:(1)因为,
∴,即,∴.
(2)因为,,,所以,
所以的整数值为4或5或6或7或8.
(3)因为,所以,即,
故第1次运算:,11的算术平方根为;
因为,所以,即,
第2次运算:,的算术平方根为;
因为,所以,即,
第3次运算:,1的算术平方根为1.故对实数经过3次运算之后的结果是1.
22.(1)解:过点D作,垂足分别为E,F,过点A作,垂足为H
由探索新知,是 ABC的角平分线时,,
∵,,∴.设,,
∴,∴.
(2)解:过点D作,垂足分别为E,F,过点A作,垂足为H
由探索新知可知,对于 ABC,是角平分线时:
,;,
∵;∴.∵,∴.故答案为;(
(3)∵平分,∴点D到,的距离相等,∴,
∵,∴,,同理平分,
∴,∴,,
连接,过点F作,,分别垂直于,,,
∵平分,平分,∴,,∴
∴平分,∴点F到,,三边的距离相等,
∴,
∵;∴,,,
∴.故答案为.
23.解:(1)两个边长为1的小正方形 ,合成一个大正方形面积为2,
大正方形的边长为; 正方形的对角线与边长的比是,故答案为:;
(2)根据图2的面积关系发现:纸面积是纸面积的2倍,纸周长是纸周长2倍;
故答案为:2,2;
(3)解:由折叠的性质可知,由(1)可知在正方形中,
,即A4纸的长宽之比为;
(4)解:由(3)可知:纸的长与宽之比是
设纸的宽为,则长为,纸的面积为,,
,,
;故纸的宽约为,长约为.
24.解:(1)∵在 ABC中,,,∴,
∵将沿折叠,点C落在上,点C的对应点为,如图1所示:∴,
∵,∴,∴;
(2),与之间的数量关系是:,理由如下:
将边折叠,使落在边上,点C的对应点为,折痕与交于点D,如图2所示:
根据折叠的性质得:,,,∵,∴,
又∵,∴,
∴,∴,∴,∴;
(3)将边折叠,使落在边上,点C的对应点为,折痕与交于点D,如图3所示:
根据折叠的性质得:,,,
在中,,,∴,∴,
∵,∴,∴,
∴,∴,∵,,∴,
在中,,∴,∴;
(4)在 ABC中,,,∴,如图4所示:
设,∴,∴,
根据折叠的性质得:,,
∴,
∵将向下折叠,使边与重合,折痕为(F在边上),∴,
∴,∴,
在中,,,,
当是等腰三角形时,有以下三种情况:
当时,则,∴,解得:,∴;
当时,则,∴,解得:,∴;
当时,则,∴,解得:,∴,
综上所述:当是等腰三角形时,的度数为或或.
25.(1)解:,
,
又,, ,
由.故答案为:;.
(2)解:①作交直线于E,则,
,,
∵,∴,∴,
又∵,,∴,
∴,∴,∴,
又∵,,∴,∴.
②作交直线于E,则,
由①得,,,,,,
∴ ×BP×AC=3× ×AM×QE,,设,则,
∴CP=BP -BC=3x-1,,
∴3x-1=1-2x,解得:,∴BP=3x=.
26.(1)解:延长到点E.使,连接,
∵是的中线,∴,又,
∴,∴,
∵在中,,∴,
∵,∴,∴;
(2)证明:延长至G,使,连接,则
∵点D为的中点,∴,
在和中,∴,∴,,
∵,∴,∵,∴,
∴,
在和中,∴,∴.
(3)解:如图,延长到G,使得,连接,延长到H,使得,连接,
∵点F是边的中点,∴,∵,∴,
∴,,∴,∴,
∵,∴,
∵,∴.∴,,
∵,∴,∴,∴.
同课章节目录
