4.6利用相似三角形测高同步练习(含解析)北师大版数学九年级上册
文档属性
| 名称 | 4.6利用相似三角形测高同步练习(含解析)北师大版数学九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-26 15:35:37 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
4.6利用相似三角形测高
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,某仓库阳光从窗户射入照到地面上,垂直地面的窗户边框在地面上的影长,窗户下檐到地面的距离,那么窗户的高为( )m.
A. B. C. D.
2.如图,三角板在灯光照射下形成投影,三角板与其投影的相似比为,且三角板的一边长为.则投影三角板的对应边长为( )
A. B. C. D.
3.如图,点光源O射出的光线沿直线传播,将胶片上的建筑物图片投影到与胶片平行的屏幕上,形成影像.已知,点光源到胶片的距离长为,长为,则胶片与屏幕的距离为( )
A.86 B.84 C.80 D.78
4.已知一个直角三角形两直角边长之和为,则这个直角三角形的最大面积为( )
A. B. C. D.
5.1m长的标杆直立在水平地面上,它在阳光下的影子长度为0.8m,同一时刻,某电视塔的影子长度为100m,则该电视塔的高度为( )
A.150m B.125m C.120m D.80m
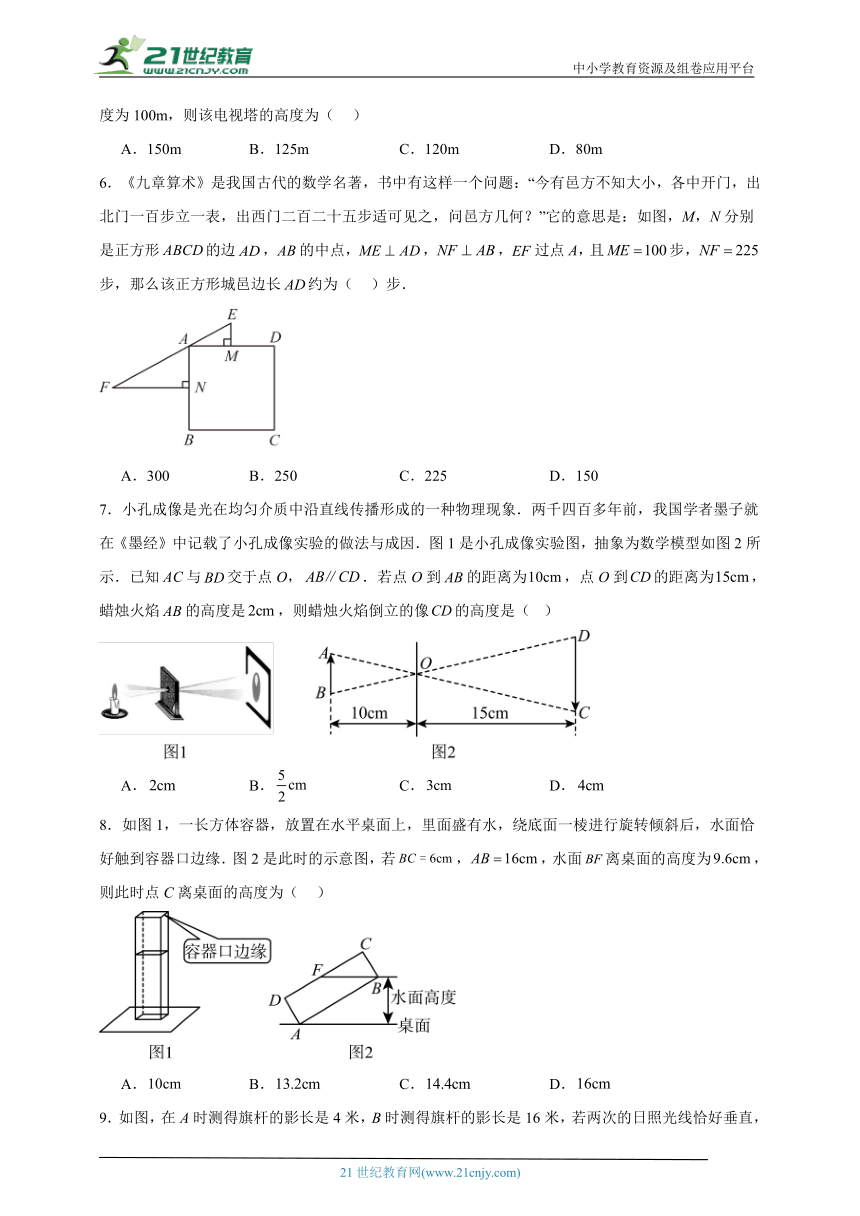
6.《九章算术》是我国古代的数学名著,书中有这样一个问题:“今有邑方不知大小,各中开门,出北门一百步立一表,出西门二百二十五步适可见之,问邑方几何?”它的意思是:如图,M,N分别是正方形的边,的中点,,,过点A,且步,步,那么该正方形城邑边长约为( )步.
A.300 B.250 C.225 D.150
7.小孔成像是光在均匀介质中沿直线传播形成的一种物理现象.两千四百多年前,我国学者墨子就在《墨经》中记载了小孔成像实验的做法与成因.图1是小孔成像实验图,抽象为数学模型如图2所示.已知与交于点O,.若点O到的距离为,点O到的距离为,蜡烛火焰的高度是,则蜡烛火焰倒立的像的高度是( )
A. B. C. D.
8.如图1,一长方体容器,放置在水平桌面上,里面盛有水,绕底面一棱进行旋转倾斜后,水面恰好触到容器口边缘.图2是此时的示意图,若,,水面离桌面的高度为,则此时点C离桌面的高度为( )
A. B. C. D.
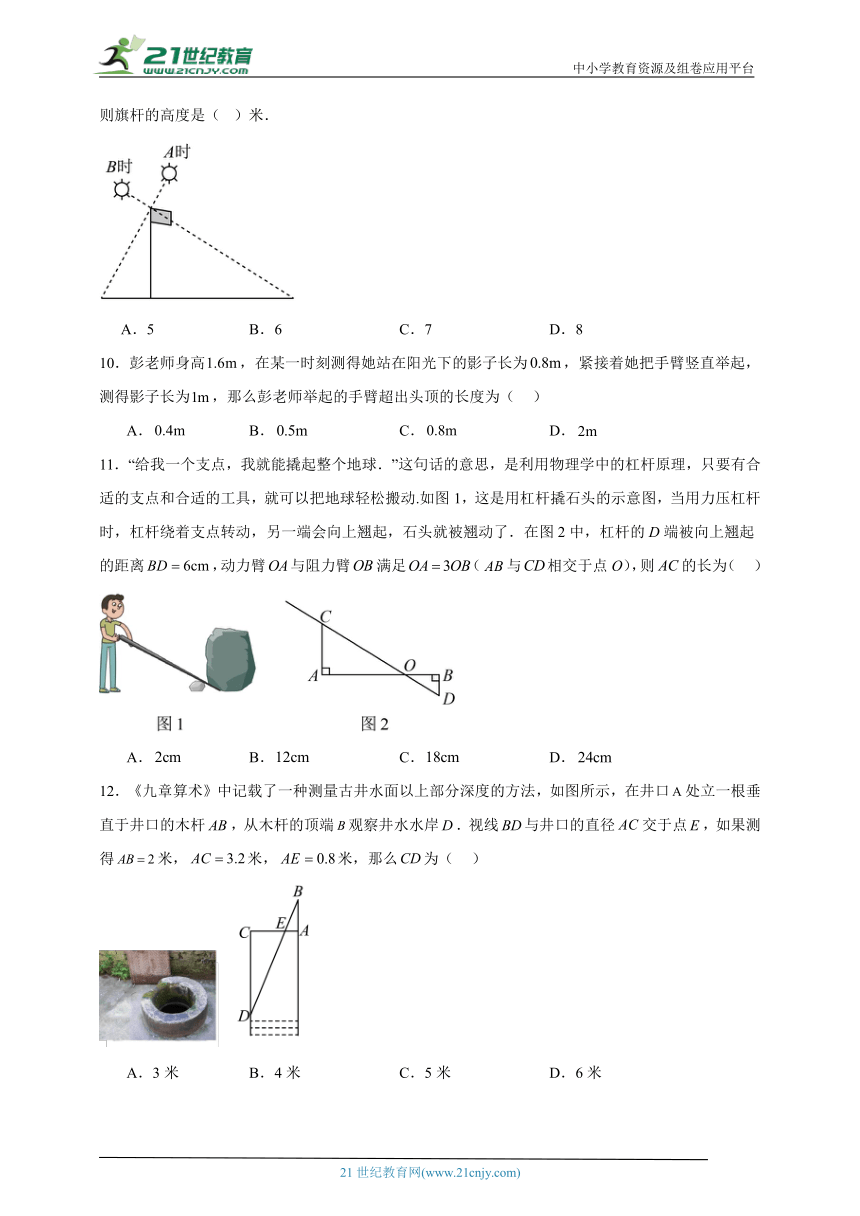
9.如图,在A时测得旗杆的影长是4米,B时测得旗杆的影长是16米,若两次的日照光线恰好垂直,则旗杆的高度是( )米.
A.5 B.6 C.7 D.8
10.彭老师身高,在某一时刻测得她站在阳光下的影子长为,紧接着她把手臂竖直举起,测得影子长为,那么彭老师举起的手臂超出头顶的长度为( )
A. B. C. D.
11.“给我一个支点,我就能撬起整个地球.”这句话的意思,是利用物理学中的杠杆原理,只要有合适的支点和合适的工具,就可以把地球轻松搬动.如图1,这是用杠杆撬石头的示意图,当用力压杠杆时,杠杆绕着支点转动,另一端会向上翘起,石头就被翘动了.在图2中,杠杆的D端被向上翘起的距离,动力臂与阻力臂满足(与相交于点O),则的长为( )
A. B. C. D.
12.《九章算术》中记载了一种测量古井水面以上部分深度的方法,如图所示,在井口处立一根垂直于井口的木杆,从木杆的顶端观察井水水岸.视线与井口的直径交于点,如果测得米,米,米,那么为( )
A.3米 B.4米 C.5米 D.6米
二、填空题
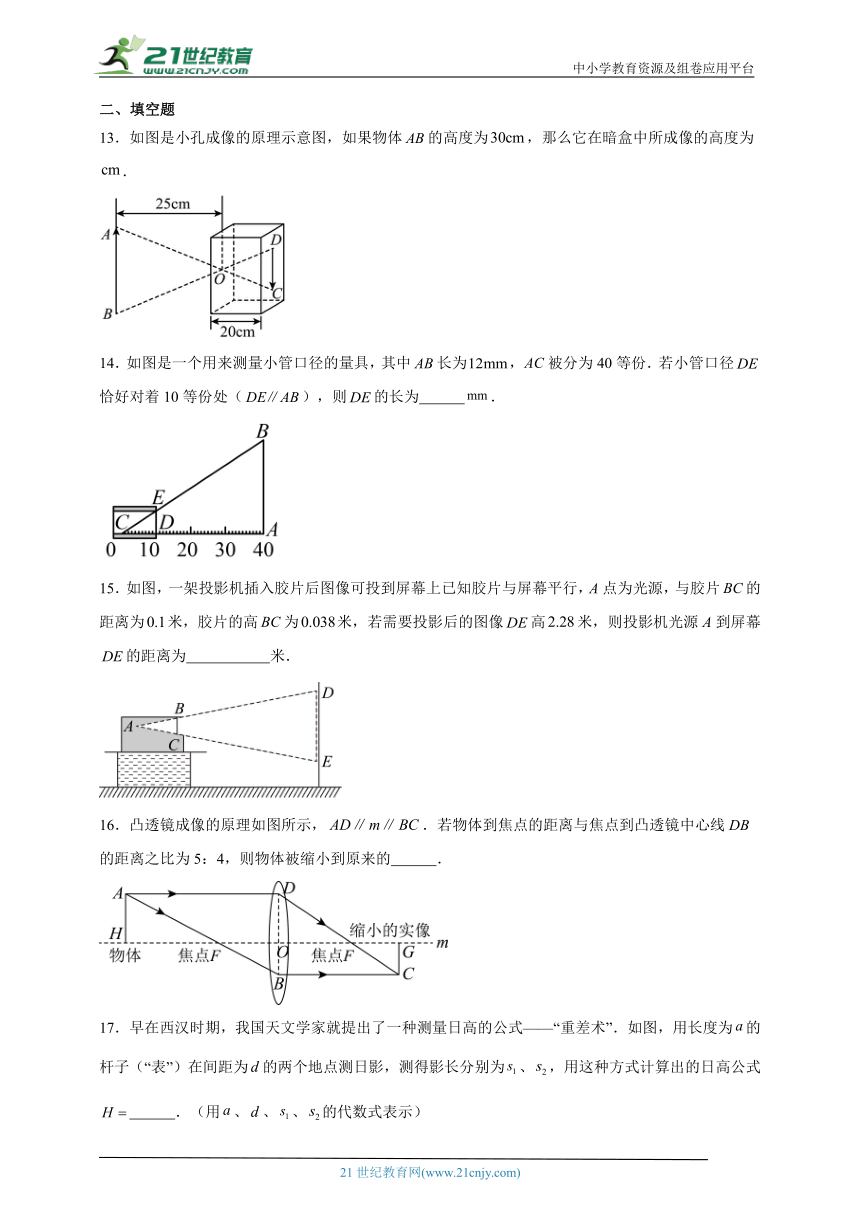
13.如图是小孔成像的原理示意图,如果物体的高度为,那么它在暗盒中所成像的高度为 .
14.如图是一个用来测量小管口径的量具,其中长为,被分为40等份.若小管口径恰好对着10等份处(),则的长为 .
15.如图,一架投影机插入胶片后图像可投到屏幕上已知胶片与屏幕平行,A点为光源,与胶片的距离为米,胶片的高为米,若需要投影后的图像高米,则投影机光源A到屏幕的距离为 米.
16.凸透镜成像的原理如图所示,.若物体到焦点的距离与焦点到凸透镜中心线DB的距离之比为5:4,则物体被缩小到原来的 .
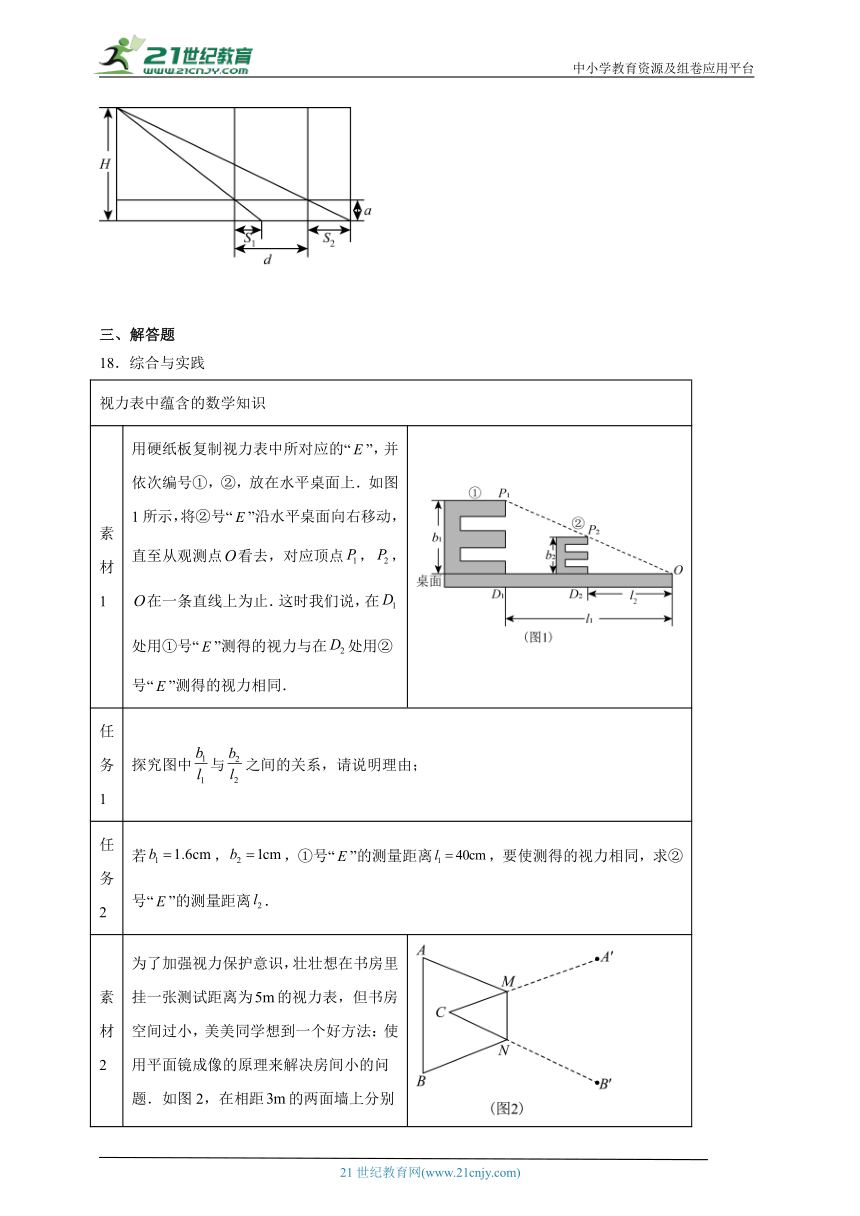
17.早在西汉时期,我国天文学家就提出了一种测量日高的公式——“重差术”.如图,用长度为的杆子(“表”)在间距为的两个地点测日影,测得影长分别为、,用这种方式计算出的日高公式 .(用、、、的代数式表示)
三、解答题
18.综合与实践
视力表中蕴含的数学知识
素材1 用硬纸板复制视力表中所对应的“”,并依次编号①,②,放在水平桌面上.如图1所示,将②号“”沿水平桌面向右移动,直至从观测点看去,对应顶点,,在一条直线上为止.这时我们说,在处用①号“”测得的视力与在处用②号“”测得的视力相同.
任务1 探究图中与之间的关系,请说明理由;
任务2 若,,①号“”的测量距离,要使测得的视力相同,求②号“”的测量距离.
素材2 为了加强视力保护意识,壮壮想在书房里挂一张测试距离为的视力表,但书房空间过小,美美同学想到一个好方法:使用平面镜成像的原理来解决房间小的问题.如图2,在相距的两面墙上分别悬挂视力表与平面镜,由平面镜成像原理,作出了光路图,通过调整人的位置,使得视力表的上、下边沿发出的光线经平面镜的上下边沿反射后射入人眼处,通过测量视力表的全长就可以计算出镜长.
任务3 美美的方法中如果视力表的全长为,请计算出镜长至少为多少米.
19.已知菱形的两条对角线长度之和恰好为,面积S(单位:)随其中一条对角线的长度x(单位:)的变化而变化.
(1)请直接写出S关于x的解析式.
(2)当x的值是多少时,菱形的面积S最大?最大面积是多少?
20.景区有一口水井,距离井边米处是最深的井底,小明想知道井有多深,于是走进观察,在距离井边米处刚好能看见井底,如果小明眼睛离地面的高度米,你能计算出水井的深度吗?
21.2023年11月23日,第十批在韩中国人民志愿军烈士遗骸归国.英烈们前仆后继的牺牲奉献,换来了我们国家的富强和人民的幸福,在抗美援朝期间“跳眼法”是炮兵常用的一种简易测距方法(图1).如图2,点A为左眼,点B为右眼,点O为右千大指,点C为敌人的位置,点D为敌人正左侧方的某一个参照物(,目测的长度后,然后利用相似三角形的知识来计算C处敌人距离我方的大致距离.已知大多数人的眼距长约为厘米左右,手臂长约为厘米左右,若的估测长度为40米,那么的大致距离为多少米.
22.如图,苏海和苏洋很想知道射阳日月岛上“生态守护者——徐秀娟”雕像的高度AB,于是,他们带着测量工具来到雕像前进行测量,测量方案如下:如图,首先,苏海在C处放置一平面镜,他从点C沿后退,当退行0.9米到E处时,恰好在镜子中看到雕像顶端A的像,此时测得苏海眼睛到地面的距离为1.2米;然后,苏海沿的延长线继续后退到点G,用测倾器测得雕像的顶端A的仰角为,此时,测得米,测倾器的高度米.已知点B、C、E、G在同一水平直线上,且、、均垂直于,求雕像的高度.
23.如图,一条小河两岸分别有两棵树,记为树A和树B.小河的宽度未知,为了安全起见,数学兴趣小组成员不得通过涉水的方式测量树A与树B之间的距离,于是他们采取如下方式:
①在树B所在的河岸边选择一点C,观测对岸的树A,并记录下的距离为;
②在树B所在的河岸内侧,选择两点D,E,从点D观测树A,且A,D以及C三点共线,然后从点E观测树B与树A,并使E,B,A三点共线;
③调整D,E的位置,使,记录下的距离为;
④测量出之间的距离大约为.
数学兴趣小组的方案能否得出树A与树B之间的距离?请通过分析与计算说明.
24.《周髀算经》中记载了“平矩以正绳,偃矩以望高,覆矩以测深,卧矩以知远,环矩以为圆,合矩以为方”的方法.“矩”在古代指两条边呈直角的曲尺(即图中的).小南利用“矩”可测量大树的高度.如图,通过不断调整自己的姿势和“矩”的摆放位置,使斜边保持水平,并且边与点B在同一直线上,已知“矩”的两边长分别为,,小南的眼睛到地面的距离为,测得,求树高.
《4.6利用相似三角形测高》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D D C B B A C C D A
题号 11 12
答案 C D
1.D
【分析】本题考查了相似三角形的应用,平行投影,熟练掌握A字模型相似三角形是解题的关键.
根据题意可得:,然后证明A字模型相似,从而利用相似三角形的性质进行计算,即可解答.
【详解】解:由题意得:,
,
,
∴,
∴,
解得:,
∴窗户的高为,
故选:D.
2.D
【分析】本题主要考查相似三角形的应用:根据对应边的比等于相似比列式进行计算即可得解,
利用数学知识解决实际问题是中学数学的重要内容,解决此问题的关键在于正确理解题意的基础上建立数学模型,把实际问题转化为数学问题.
【详解】解:设投影三角尺的对应边长为,
∵三角尺与投影三角尺相似,
∴,
解得,
所以投影三角尺的对应边长为,
故选:D.
3.C
【分析】本题考查中心投影,相似三角形的判定和性质等知识,解题的关键是学会利用相似三角形的性质解决问题.证明,推出,构建方程求出即可.
【详解】解:,
,
,
,
,
,
,
故选:C.
4.B
【分析】本题考查了二次函数的最大值,求二次函数的最大(小)值有三种方法,第一种是由函数图象直接得出,第二种是配方法,第三种是公式法,本题采用配方法求解比较简单.
设一条直角边长为cm,则另一条直角边长为cm.根据直角三角形面积公式,列出关于的二次函数,利用二次函数的最大值求解.
【详解】解:设一条直角边长为cm,则另一条直角边长为cm.
直角三角形的面积为:
将面积表达式化为顶点式:
由于二次项系数,函数开口向下,当时,面积取得最大值.
此时另一条直角边为,即两直角边相等时面积最大.
故选:B
5.B
【分析】在同一时刻物高和影长成正比,即在同一时刻的两个物体,影子,经过物体顶部的太阳光线三者构成的两个直角三角形相似.
【详解】解:设电视塔的高度应是x,
根据题意得:=,
解得:x=125,
故选:B.
【点睛】本题主要考查了相似三角形的应用,利用相似比,列出方程,通过解方程求出电视塔的高度,体现了方程的思想.
6.A
【分析】本题考查相似三角形解实际应用题,读懂题意,熟练应用相似三角形的判定与性质是解决问题的关键.由题意可知,根据相似三角形性质得到,设,由分别是正方形的边的中点可知,则,解得,从而得到正方形城邑边长步.
【详解】解:,,
,
正方形中,,过点,
,则,
,
,
分别是正方形的边的中点,设,
,
步,步,
,即,解得负舍去值,
正方形城邑边长步,
故选:A.
7.C
【分析】根据,得,得到,代入计算解答即可.
本题考查了三角形相似的判定和性质,熟练掌握判定和性质是解题的关键.
【详解】解:∵,
∴,
∵点O到的距离为,点O到的距离为,蜡烛火焰的高度是,
∴,
∴,
解得,
故选:C.
8.C
【分析】本题考查了矩形的性质,勾股定理,相似三角形的判定和性质,过点C作桌面的垂线,垂足为点M,交于点N;过点B作桌面的垂线,垂足为点P;根据题意易得,通过证明,求出,再根据勾股定理求出,最后根据,即可求解.
【详解】解:过点C作桌面的垂线,垂足为点M,交于点N;过点B作桌面的垂线,垂足为点P,
∵水面离桌面的高度为,
∴,
∵,
∴,
∵,
∴,
又∵,
∴,
∴,即,
解得:,
根据勾股定理可得:,
∴,
即此时点C离桌面的高度为.
故选:C.
9.D
【分析】本题主要考查了相似三角形的应用,利用等角的余角相等得到,则可判断,然后利用相似比可计算出.
【详解】解:如图,,,,
∵,
∴,
∴,
而,
∴,
∴,
∴ ,
即,
∴,
即旗杆的高度为.
故选:D
10.A
【分析】此题考查相似三角形的应用,能够根据同一时刻物高与影长成比例,列出正确的比例式,然后根据比例的基本性质进行求解即可.
【详解】解:解:设彭老师举起的手臂超出头顶是,根据同一时刻物高与影长成比例,得,
解得:.
故选:A.
11.C
【分析】本题考查相似三角形的判定与性质的实际应用,首先根据题意构造出相似三角形,然后根据相似三角形的对应边成比例求得端点C向下压的长度是解题的关键.
【详解】解:解:由题意得,,
∴,,
∴,
∴,
∵,
∴,
∴,
故选C.
12.D
【分析】本题考查了相似三角形的应用,由题意知:,得出对应边成比例即可得出.根据题意得出是解决问题的关键.
【详解】解:由题意知:,则,,
∴,
∴,
∴,
∴,
经检验,是所列方程的解,
故选:D.
13.
【分析】本题考查了相似三角形的判定与性质,由题意得出,从而得出,由相似三角形的性质可得,代入计算即可得出答案.
【详解】解:由题意得:,
,
,
,
,
故答案为:.
14.
【分析】本题考查了相似三角形的应用,正确理解题意是解题的关键.由得,再根据相似三角形的性质,即可求得答案.
【详解】,
,
,
,,,
,
解得.
故答案为:.
15.6
【分析】本题考查的是相似三角形在实际生活中的运用,因为光源与胶片组成的三角形与光源与投影后的图象组成的三角形相似,所以可用相似三角形的相似比解答.
【详解】解:如图所示,过A作于G,交与F,
因为,
所以,,米,
设,
则,即,
解得:,
米,
故答案为:6.
16./
【分析】本题考查了相似三角形的应用,根据题意可得四边形为矩形,得到,再根据,求出,从而得到物体被缩小到原来的几分之几.
【详解】解:依题意,四边形为矩形,设左边交点为
∴,
∵,,
∴,
∴,
∴,即
∴物体被缩小到原来的.
故答案为:.
17.
【分析】本题主要考查了相似三角形的判定与性质,根据,,即:,可得,同理,可得,即:,则有,问题随之得解.
【详解】如图,
根据题意有:,,,,,,,,
∴,,
∴,
∴,
∴,即:,
∴,
同理,
∴,即:,
∴,
∵,
∴,
∴,
故答案为:.
18.任务1:,理由见解析;任务2:②号“”的测量距离为;任务3:镜长至少为
【分析】本题考查了相似三角形的判定与性质,熟练掌握相似三角形的判定与性质,理解题意,采用数形结合的思想是解此题的关键.
任务1:根据相似三角形的对应边成比例解答;
任务2:根据相似三角形的对应边成比例代入数据进行计算即可;
任务3:根据相似三角形的对应边成比例代入数据进行计算即可.
【详解】解:任务1:,
理由如下:,
,
,即;
任务2:,且,,,
,
,
②号“”的测量距离为;
任务3:如图,延长至,使,延长至,使,连接,作于,交于,
,
则,,
,,
,
由题意得:,,
,
,
,
镜长至少为.
19.(1)
(2)当时,菱形的面积S最大,最大面积是
【分析】.此题主要考查了二次函数的应用以及菱形的性质,根据菱形的面积等于对角线乘积的一半得出函数关系式是解决问题的关键.
(1)根据菱形的面积等于对角线乘积的一半,即可得出S与x之间的函数关系式;
(2)根据二次函数当时,二次函数有最小(大)值,求出即可.
【详解】(1)解:∵菱形的两条对角线长度之和恰好为,其中一条对角线的长为x,
∴另外一条对角线的长为
.
(2)解:,且,
当时,S有最大值,最大值是450.
故当时,菱形的面积S最大,最大面积是.
20.10米
【分析】本题考查的是相似三角形的应用举例,先证明,可得,从而可得答案;
【详解】解:,
,
,
,
,
,
米.
21.
【分析】本题主要考查了相似三角形的应用,证明得到,再代值计算即可得到答案.
【详解】解:,
∴,
,
,
根据题意得,,,,
,
答:的大致距离为.
22.
【分析】根据已知条件推出,求得与的关系,再根据题意易得四边形、四边形、四边形均为矩形,得到,根据,得,构造一元一次方程,解方程即可得出结论.
【详解】解:设米,如图,
根据题意可得,,,
∴,
∴,
∴,
∵点B、C、E、G在同一水平直线上,且、、均垂直于,,
∴四边形、四边形、四边形均为矩形,
∴,
∵,
∴,
∴
解得
∴
答:雕像的高度为16.8米.
【点睛】本题考查相似三角形的判定、性质与实际应用,熟练掌握相关知识点是解题的关键.
23.能测出树A与树B之间的距离为18米
【分析】本题主要考查了相似三角形的应用,根据平行证明,即可得,代入计算即可作答.
【详解】能测出树A与树B之间的距离,如下:
∵,
∴,,
∴,
∴,即,
∵的距离为,的距离为,之间的距离大约为,
∴,
解得:,
经检验,是原方程的解,
答:能测出树A与树B之间的距离为18米.
24.树高为
【分析】本题主要考查了相似三角形的应用举例,据题意可得,,即可得出,由相似三角形的性质可得出,即可得出,再根据即可得出答案.
【详解】解:据题意可得,,
,
.
,,,
,
,
.
答:树高为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
4.6利用相似三角形测高
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,某仓库阳光从窗户射入照到地面上,垂直地面的窗户边框在地面上的影长,窗户下檐到地面的距离,那么窗户的高为( )m.
A. B. C. D.
2.如图,三角板在灯光照射下形成投影,三角板与其投影的相似比为,且三角板的一边长为.则投影三角板的对应边长为( )
A. B. C. D.
3.如图,点光源O射出的光线沿直线传播,将胶片上的建筑物图片投影到与胶片平行的屏幕上,形成影像.已知,点光源到胶片的距离长为,长为,则胶片与屏幕的距离为( )
A.86 B.84 C.80 D.78
4.已知一个直角三角形两直角边长之和为,则这个直角三角形的最大面积为( )
A. B. C. D.
5.1m长的标杆直立在水平地面上,它在阳光下的影子长度为0.8m,同一时刻,某电视塔的影子长度为100m,则该电视塔的高度为( )
A.150m B.125m C.120m D.80m
6.《九章算术》是我国古代的数学名著,书中有这样一个问题:“今有邑方不知大小,各中开门,出北门一百步立一表,出西门二百二十五步适可见之,问邑方几何?”它的意思是:如图,M,N分别是正方形的边,的中点,,,过点A,且步,步,那么该正方形城邑边长约为( )步.
A.300 B.250 C.225 D.150
7.小孔成像是光在均匀介质中沿直线传播形成的一种物理现象.两千四百多年前,我国学者墨子就在《墨经》中记载了小孔成像实验的做法与成因.图1是小孔成像实验图,抽象为数学模型如图2所示.已知与交于点O,.若点O到的距离为,点O到的距离为,蜡烛火焰的高度是,则蜡烛火焰倒立的像的高度是( )
A. B. C. D.
8.如图1,一长方体容器,放置在水平桌面上,里面盛有水,绕底面一棱进行旋转倾斜后,水面恰好触到容器口边缘.图2是此时的示意图,若,,水面离桌面的高度为,则此时点C离桌面的高度为( )
A. B. C. D.
9.如图,在A时测得旗杆的影长是4米,B时测得旗杆的影长是16米,若两次的日照光线恰好垂直,则旗杆的高度是( )米.
A.5 B.6 C.7 D.8
10.彭老师身高,在某一时刻测得她站在阳光下的影子长为,紧接着她把手臂竖直举起,测得影子长为,那么彭老师举起的手臂超出头顶的长度为( )
A. B. C. D.
11.“给我一个支点,我就能撬起整个地球.”这句话的意思,是利用物理学中的杠杆原理,只要有合适的支点和合适的工具,就可以把地球轻松搬动.如图1,这是用杠杆撬石头的示意图,当用力压杠杆时,杠杆绕着支点转动,另一端会向上翘起,石头就被翘动了.在图2中,杠杆的D端被向上翘起的距离,动力臂与阻力臂满足(与相交于点O),则的长为( )
A. B. C. D.
12.《九章算术》中记载了一种测量古井水面以上部分深度的方法,如图所示,在井口处立一根垂直于井口的木杆,从木杆的顶端观察井水水岸.视线与井口的直径交于点,如果测得米,米,米,那么为( )
A.3米 B.4米 C.5米 D.6米
二、填空题
13.如图是小孔成像的原理示意图,如果物体的高度为,那么它在暗盒中所成像的高度为 .
14.如图是一个用来测量小管口径的量具,其中长为,被分为40等份.若小管口径恰好对着10等份处(),则的长为 .
15.如图,一架投影机插入胶片后图像可投到屏幕上已知胶片与屏幕平行,A点为光源,与胶片的距离为米,胶片的高为米,若需要投影后的图像高米,则投影机光源A到屏幕的距离为 米.
16.凸透镜成像的原理如图所示,.若物体到焦点的距离与焦点到凸透镜中心线DB的距离之比为5:4,则物体被缩小到原来的 .
17.早在西汉时期,我国天文学家就提出了一种测量日高的公式——“重差术”.如图,用长度为的杆子(“表”)在间距为的两个地点测日影,测得影长分别为、,用这种方式计算出的日高公式 .(用、、、的代数式表示)
三、解答题
18.综合与实践
视力表中蕴含的数学知识
素材1 用硬纸板复制视力表中所对应的“”,并依次编号①,②,放在水平桌面上.如图1所示,将②号“”沿水平桌面向右移动,直至从观测点看去,对应顶点,,在一条直线上为止.这时我们说,在处用①号“”测得的视力与在处用②号“”测得的视力相同.
任务1 探究图中与之间的关系,请说明理由;
任务2 若,,①号“”的测量距离,要使测得的视力相同,求②号“”的测量距离.
素材2 为了加强视力保护意识,壮壮想在书房里挂一张测试距离为的视力表,但书房空间过小,美美同学想到一个好方法:使用平面镜成像的原理来解决房间小的问题.如图2,在相距的两面墙上分别悬挂视力表与平面镜,由平面镜成像原理,作出了光路图,通过调整人的位置,使得视力表的上、下边沿发出的光线经平面镜的上下边沿反射后射入人眼处,通过测量视力表的全长就可以计算出镜长.
任务3 美美的方法中如果视力表的全长为,请计算出镜长至少为多少米.
19.已知菱形的两条对角线长度之和恰好为,面积S(单位:)随其中一条对角线的长度x(单位:)的变化而变化.
(1)请直接写出S关于x的解析式.
(2)当x的值是多少时,菱形的面积S最大?最大面积是多少?
20.景区有一口水井,距离井边米处是最深的井底,小明想知道井有多深,于是走进观察,在距离井边米处刚好能看见井底,如果小明眼睛离地面的高度米,你能计算出水井的深度吗?
21.2023年11月23日,第十批在韩中国人民志愿军烈士遗骸归国.英烈们前仆后继的牺牲奉献,换来了我们国家的富强和人民的幸福,在抗美援朝期间“跳眼法”是炮兵常用的一种简易测距方法(图1).如图2,点A为左眼,点B为右眼,点O为右千大指,点C为敌人的位置,点D为敌人正左侧方的某一个参照物(,目测的长度后,然后利用相似三角形的知识来计算C处敌人距离我方的大致距离.已知大多数人的眼距长约为厘米左右,手臂长约为厘米左右,若的估测长度为40米,那么的大致距离为多少米.
22.如图,苏海和苏洋很想知道射阳日月岛上“生态守护者——徐秀娟”雕像的高度AB,于是,他们带着测量工具来到雕像前进行测量,测量方案如下:如图,首先,苏海在C处放置一平面镜,他从点C沿后退,当退行0.9米到E处时,恰好在镜子中看到雕像顶端A的像,此时测得苏海眼睛到地面的距离为1.2米;然后,苏海沿的延长线继续后退到点G,用测倾器测得雕像的顶端A的仰角为,此时,测得米,测倾器的高度米.已知点B、C、E、G在同一水平直线上,且、、均垂直于,求雕像的高度.
23.如图,一条小河两岸分别有两棵树,记为树A和树B.小河的宽度未知,为了安全起见,数学兴趣小组成员不得通过涉水的方式测量树A与树B之间的距离,于是他们采取如下方式:
①在树B所在的河岸边选择一点C,观测对岸的树A,并记录下的距离为;
②在树B所在的河岸内侧,选择两点D,E,从点D观测树A,且A,D以及C三点共线,然后从点E观测树B与树A,并使E,B,A三点共线;
③调整D,E的位置,使,记录下的距离为;
④测量出之间的距离大约为.
数学兴趣小组的方案能否得出树A与树B之间的距离?请通过分析与计算说明.
24.《周髀算经》中记载了“平矩以正绳,偃矩以望高,覆矩以测深,卧矩以知远,环矩以为圆,合矩以为方”的方法.“矩”在古代指两条边呈直角的曲尺(即图中的).小南利用“矩”可测量大树的高度.如图,通过不断调整自己的姿势和“矩”的摆放位置,使斜边保持水平,并且边与点B在同一直线上,已知“矩”的两边长分别为,,小南的眼睛到地面的距离为,测得,求树高.
《4.6利用相似三角形测高》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D D C B B A C C D A
题号 11 12
答案 C D
1.D
【分析】本题考查了相似三角形的应用,平行投影,熟练掌握A字模型相似三角形是解题的关键.
根据题意可得:,然后证明A字模型相似,从而利用相似三角形的性质进行计算,即可解答.
【详解】解:由题意得:,
,
,
∴,
∴,
解得:,
∴窗户的高为,
故选:D.
2.D
【分析】本题主要考查相似三角形的应用:根据对应边的比等于相似比列式进行计算即可得解,
利用数学知识解决实际问题是中学数学的重要内容,解决此问题的关键在于正确理解题意的基础上建立数学模型,把实际问题转化为数学问题.
【详解】解:设投影三角尺的对应边长为,
∵三角尺与投影三角尺相似,
∴,
解得,
所以投影三角尺的对应边长为,
故选:D.
3.C
【分析】本题考查中心投影,相似三角形的判定和性质等知识,解题的关键是学会利用相似三角形的性质解决问题.证明,推出,构建方程求出即可.
【详解】解:,
,
,
,
,
,
,
故选:C.
4.B
【分析】本题考查了二次函数的最大值,求二次函数的最大(小)值有三种方法,第一种是由函数图象直接得出,第二种是配方法,第三种是公式法,本题采用配方法求解比较简单.
设一条直角边长为cm,则另一条直角边长为cm.根据直角三角形面积公式,列出关于的二次函数,利用二次函数的最大值求解.
【详解】解:设一条直角边长为cm,则另一条直角边长为cm.
直角三角形的面积为:
将面积表达式化为顶点式:
由于二次项系数,函数开口向下,当时,面积取得最大值.
此时另一条直角边为,即两直角边相等时面积最大.
故选:B
5.B
【分析】在同一时刻物高和影长成正比,即在同一时刻的两个物体,影子,经过物体顶部的太阳光线三者构成的两个直角三角形相似.
【详解】解:设电视塔的高度应是x,
根据题意得:=,
解得:x=125,
故选:B.
【点睛】本题主要考查了相似三角形的应用,利用相似比,列出方程,通过解方程求出电视塔的高度,体现了方程的思想.
6.A
【分析】本题考查相似三角形解实际应用题,读懂题意,熟练应用相似三角形的判定与性质是解决问题的关键.由题意可知,根据相似三角形性质得到,设,由分别是正方形的边的中点可知,则,解得,从而得到正方形城邑边长步.
【详解】解:,,
,
正方形中,,过点,
,则,
,
,
分别是正方形的边的中点,设,
,
步,步,
,即,解得负舍去值,
正方形城邑边长步,
故选:A.
7.C
【分析】根据,得,得到,代入计算解答即可.
本题考查了三角形相似的判定和性质,熟练掌握判定和性质是解题的关键.
【详解】解:∵,
∴,
∵点O到的距离为,点O到的距离为,蜡烛火焰的高度是,
∴,
∴,
解得,
故选:C.
8.C
【分析】本题考查了矩形的性质,勾股定理,相似三角形的判定和性质,过点C作桌面的垂线,垂足为点M,交于点N;过点B作桌面的垂线,垂足为点P;根据题意易得,通过证明,求出,再根据勾股定理求出,最后根据,即可求解.
【详解】解:过点C作桌面的垂线,垂足为点M,交于点N;过点B作桌面的垂线,垂足为点P,
∵水面离桌面的高度为,
∴,
∵,
∴,
∵,
∴,
又∵,
∴,
∴,即,
解得:,
根据勾股定理可得:,
∴,
即此时点C离桌面的高度为.
故选:C.
9.D
【分析】本题主要考查了相似三角形的应用,利用等角的余角相等得到,则可判断,然后利用相似比可计算出.
【详解】解:如图,,,,
∵,
∴,
∴,
而,
∴,
∴,
∴ ,
即,
∴,
即旗杆的高度为.
故选:D
10.A
【分析】此题考查相似三角形的应用,能够根据同一时刻物高与影长成比例,列出正确的比例式,然后根据比例的基本性质进行求解即可.
【详解】解:解:设彭老师举起的手臂超出头顶是,根据同一时刻物高与影长成比例,得,
解得:.
故选:A.
11.C
【分析】本题考查相似三角形的判定与性质的实际应用,首先根据题意构造出相似三角形,然后根据相似三角形的对应边成比例求得端点C向下压的长度是解题的关键.
【详解】解:解:由题意得,,
∴,,
∴,
∴,
∵,
∴,
∴,
故选C.
12.D
【分析】本题考查了相似三角形的应用,由题意知:,得出对应边成比例即可得出.根据题意得出是解决问题的关键.
【详解】解:由题意知:,则,,
∴,
∴,
∴,
∴,
经检验,是所列方程的解,
故选:D.
13.
【分析】本题考查了相似三角形的判定与性质,由题意得出,从而得出,由相似三角形的性质可得,代入计算即可得出答案.
【详解】解:由题意得:,
,
,
,
,
故答案为:.
14.
【分析】本题考查了相似三角形的应用,正确理解题意是解题的关键.由得,再根据相似三角形的性质,即可求得答案.
【详解】,
,
,
,,,
,
解得.
故答案为:.
15.6
【分析】本题考查的是相似三角形在实际生活中的运用,因为光源与胶片组成的三角形与光源与投影后的图象组成的三角形相似,所以可用相似三角形的相似比解答.
【详解】解:如图所示,过A作于G,交与F,
因为,
所以,,米,
设,
则,即,
解得:,
米,
故答案为:6.
16./
【分析】本题考查了相似三角形的应用,根据题意可得四边形为矩形,得到,再根据,求出,从而得到物体被缩小到原来的几分之几.
【详解】解:依题意,四边形为矩形,设左边交点为
∴,
∵,,
∴,
∴,
∴,即
∴物体被缩小到原来的.
故答案为:.
17.
【分析】本题主要考查了相似三角形的判定与性质,根据,,即:,可得,同理,可得,即:,则有,问题随之得解.
【详解】如图,
根据题意有:,,,,,,,,
∴,,
∴,
∴,
∴,即:,
∴,
同理,
∴,即:,
∴,
∵,
∴,
∴,
故答案为:.
18.任务1:,理由见解析;任务2:②号“”的测量距离为;任务3:镜长至少为
【分析】本题考查了相似三角形的判定与性质,熟练掌握相似三角形的判定与性质,理解题意,采用数形结合的思想是解此题的关键.
任务1:根据相似三角形的对应边成比例解答;
任务2:根据相似三角形的对应边成比例代入数据进行计算即可;
任务3:根据相似三角形的对应边成比例代入数据进行计算即可.
【详解】解:任务1:,
理由如下:,
,
,即;
任务2:,且,,,
,
,
②号“”的测量距离为;
任务3:如图,延长至,使,延长至,使,连接,作于,交于,
,
则,,
,,
,
由题意得:,,
,
,
,
镜长至少为.
19.(1)
(2)当时,菱形的面积S最大,最大面积是
【分析】.此题主要考查了二次函数的应用以及菱形的性质,根据菱形的面积等于对角线乘积的一半得出函数关系式是解决问题的关键.
(1)根据菱形的面积等于对角线乘积的一半,即可得出S与x之间的函数关系式;
(2)根据二次函数当时,二次函数有最小(大)值,求出即可.
【详解】(1)解:∵菱形的两条对角线长度之和恰好为,其中一条对角线的长为x,
∴另外一条对角线的长为
.
(2)解:,且,
当时,S有最大值,最大值是450.
故当时,菱形的面积S最大,最大面积是.
20.10米
【分析】本题考查的是相似三角形的应用举例,先证明,可得,从而可得答案;
【详解】解:,
,
,
,
,
,
米.
21.
【分析】本题主要考查了相似三角形的应用,证明得到,再代值计算即可得到答案.
【详解】解:,
∴,
,
,
根据题意得,,,,
,
答:的大致距离为.
22.
【分析】根据已知条件推出,求得与的关系,再根据题意易得四边形、四边形、四边形均为矩形,得到,根据,得,构造一元一次方程,解方程即可得出结论.
【详解】解:设米,如图,
根据题意可得,,,
∴,
∴,
∴,
∵点B、C、E、G在同一水平直线上,且、、均垂直于,,
∴四边形、四边形、四边形均为矩形,
∴,
∵,
∴,
∴
解得
∴
答:雕像的高度为16.8米.
【点睛】本题考查相似三角形的判定、性质与实际应用,熟练掌握相关知识点是解题的关键.
23.能测出树A与树B之间的距离为18米
【分析】本题主要考查了相似三角形的应用,根据平行证明,即可得,代入计算即可作答.
【详解】能测出树A与树B之间的距离,如下:
∵,
∴,,
∴,
∴,即,
∵的距离为,的距离为,之间的距离大约为,
∴,
解得:,
经检验,是原方程的解,
答:能测出树A与树B之间的距离为18米.
24.树高为
【分析】本题主要考查了相似三角形的应用举例,据题意可得,,即可得出,由相似三角形的性质可得出,即可得出,再根据即可得出答案.
【详解】解:据题意可得,,
,
.
,,,
,
,
.
答:树高为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
