2024-2025学年山东省淄博市博山区七年级(下)期末数学试卷(五四学制)(含答案)
文档属性
| 名称 | 2024-2025学年山东省淄博市博山区七年级(下)期末数学试卷(五四学制)(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 977.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-25 00:00:00 | ||
图片预览



文档简介
2024-2025学年山东省淄博市博山区七年级(下)期末数学试卷(五四学制)
一、选择题:本大题共12个小题,每小题4分,共48分。在每小题所给出的四个选项中,只有一项是符合题目要求的。
1.(4分)下列解集中,包括2的是( )
A.x<2 B.x≥3 C.x≤3 D.x>2
2.(4分)掷一枚质地均匀的骰子2次,向上一面的点数和是13.这个事件是( )
A.随机事件 B.不可能事件
C.必然事件 D.无法确定
3.(4分)如图:在△ABC中,AB=AC,BD平分∠ABC,交AC于点D,若BD=BC,则∠A等于( )
A.30° B.36° C.40° D.42°
4.(4分)若是方程3x﹣ay=4的一个解,则a的值为( )
A.1 B.﹣1 C.3 D.2
5.(4分)判断命题“对任意实数a,都有(a+1)2>0”是假命题,只需要举出反例,反例中a的可以是( )
A.2 B.1 C.0 D.﹣1
6.(4分)如图,下列条件中,不能判断c∥d的是( )
A.∠1=∠2 B.∠3+∠5=180°
C.∠2+∠5=180° D.∠4=∠5
7.(4分)运行程序如图所示,规定:从“输入一个值x”到“结果是否>95”为一次程序操作,如果程序操作运行了两次就停止,那么x的取值范围是( )
A.23<x≤47 B.11<x≤23 C.7<x≤11 D.3<x≤7
8.(4分)如图1所示,是地理学科实践课上第一小组同学在一张面积为36cm2的长方形卡纸上绘制的山东省政区图(图中阴影部分),他们想了解该图案的面积是多少,经研究采取了以下办法:将长方形卡纸水平放置在地面上,在适当位置随机地朝长方形区域扔小球,并记录小球落在不规则图案上的次数(球扔在界线上或长方形区域外不计试验结果).他们将若干次有效试验的结果绘制成了如图2所示的统计图,由此估计不规则图案的面积大约为( )
A.55.38cm2 B.23.4cm2 C.25.2cm2 D.24.28cm2
9.(4分)如图,一次函数yx的图象与y=kx+7的图象相交于点A,则方程组的解是( )
A. B. C. D.
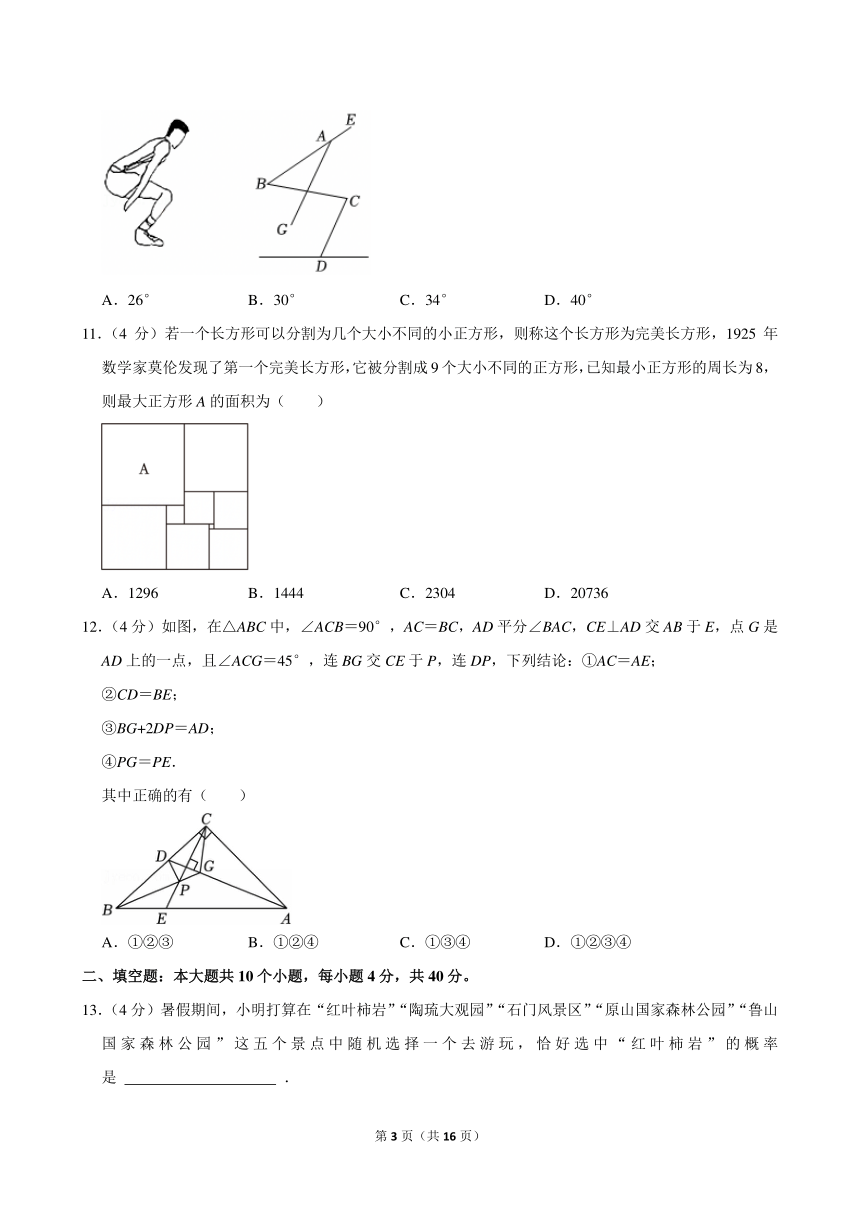
10.(4分)立定跳远动作中,从起跳到落地瞬间的几个身体相关关节的角度,对跳远成绩起着举足轻重的作用.如图是小李落地瞬间的动作及其示意图,若AG∥CD,∠BCD=74°,∠B=44°,则∠BAG的度数为( )
A.26° B.30° C.34° D.40°
11.(4分)若一个长方形可以分割为几个大小不同的小正方形,则称这个长方形为完美长方形,1925年数学家莫伦发现了第一个完美长方形,它被分割成9个大小不同的正方形,已知最小正方形的周长为8,则最大正方形A的面积为( )
A.1296 B.1444 C.2304 D.20736
12.(4分)如图,在△ABC中,∠ACB=90°,AC=BC,AD平分∠BAC,CE⊥AD交AB于E,点G是AD上的一点,且∠ACG=45°,连BG交CE于P,连DP,下列结论:①AC=AE;
②CD=BE;
③BG+2DP=AD;
④PG=PE.
其中正确的有( )
A.①②③ B.①②④ C.①③④ D.①②③④
二、填空题:本大题共10个小题,每小题4分,共40分。
13.(4分)暑假期间,小明打算在“红叶柿岩”“陶琉大观园”“石门风景区”“原山国家森林公园”“鲁山国家森林公园”这五个景点中随机选择一个去游玩,恰好选中“红叶柿岩”的概率是 .
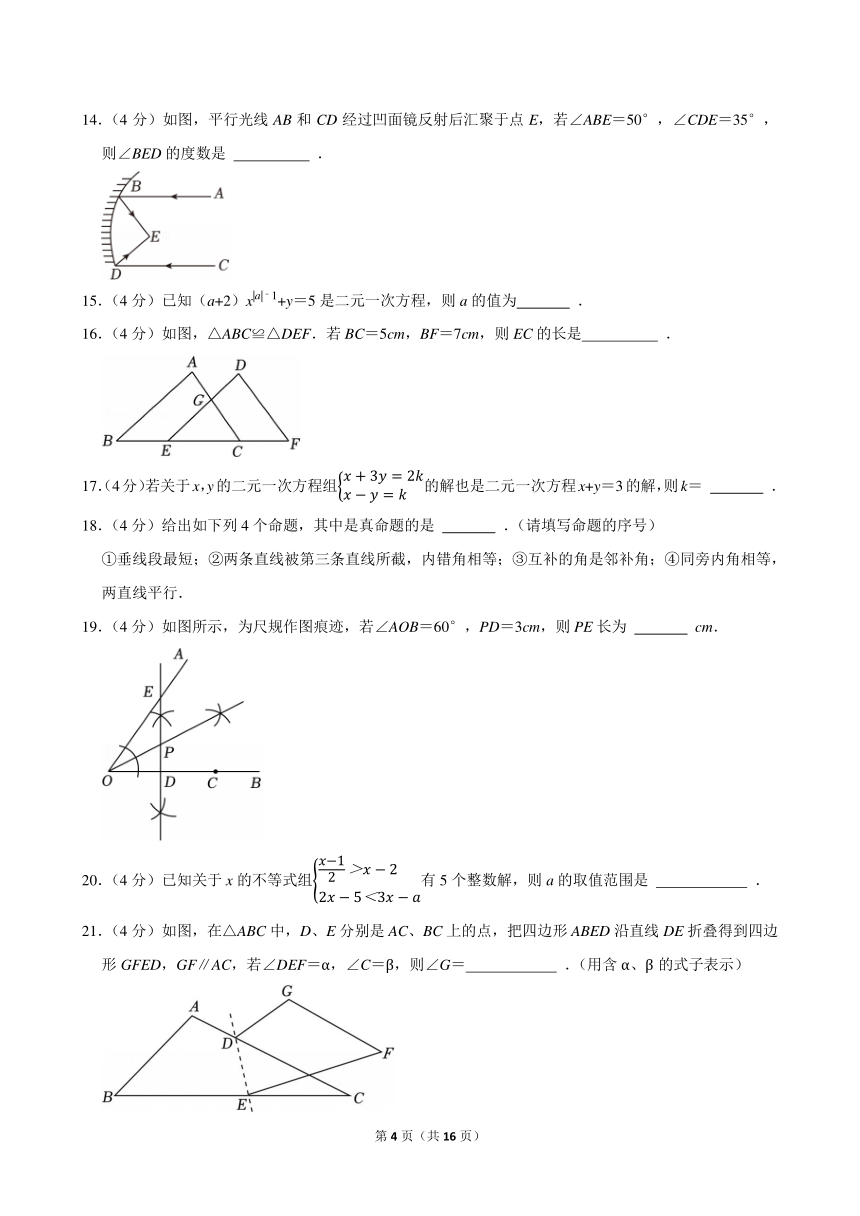
14.(4分)如图,平行光线AB和CD经过凹面镜反射后汇聚于点E,若∠ABE=50°,∠CDE=35°,则∠BED的度数是 .
15.(4分)已知(a+2)x|a|﹣1+y=5是二元一次方程,则a的值为 .
16.(4分)如图,△ABC≌△DEF.若BC=5cm,BF=7cm,则EC的长是 .
17.(4分)若关于x,y的二元一次方程组的解也是二元一次方程x+y=3的解,则k= .
18.(4分)给出如下列4个命题,其中是真命题的是 .(请填写命题的序号)
①垂线段最短;②两条直线被第三条直线所截,内错角相等;③互补的角是邻补角;④同旁内角相等,两直线平行.
19.(4分)如图所示,为尺规作图痕迹,若∠AOB=60°,PD=3cm,则PE长为 cm.
20.(4分)已知关于x的不等式组有5个整数解,则a的取值范围是 .
21.(4分)如图,在△ABC中,D、E分别是AC、BC上的点,把四边形ABED沿直线DE折叠得到四边形GFED,GF∥AC,若∠DEF=α,∠C=β,则∠G= .(用含α、β的式子表示)
22.(4分)设a1,a2, ,a2024,a2025是从﹣2,0,1这三个数取值的一组数,若a1+a2+ +a2024+a2025=950,(a1+1)2+(a2+1)2+ +(a2024+1)2+(a2025+1)2=5025,则a1,a2, ,a2024,a2025中为0的个数为 个.
三、解答题:本大题共7个小题,共62分。解答要写出必要的文字说明、证明过程或演算步骤。
23.(8分)解不等式组,并把解集在数轴上表示出来.
24.(8分)如图,B是线段AC的中点,AD∥BE,BD∥CE.求证:△ABD≌△BCE.
25.(8分)在五一期间,某商场为了吸引顾客,设立了一个可以自由转动的转盘(如图1),并规定:顾客每购买100元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红、黄或绿色区域,顾客就可以分别获得100元,50元,20元的购物券(转盘被等分成20个扇形).已知甲顾客购物150元.
(1)他得到50元的购物券的概率是多少?
(2)他获得购物券的概率是多少?
(3)请你利用图2所示转盘,设计一个转盘游戏,使得顾客获得购物券的概率是,并简要说明游戏规则.
26.(8分)如图,点D、E在AB上,点F、G分别在BC、CA上,且DG∥BC,∠1=∠2.
(1)求证:DC∥EF;
(2)若EF⊥AB,∠1=55°,求∠ADG的度数.
27.(10分)某公司用甲、乙两种货车运输原料,两次满载的运输情况如表:
甲种货车/辆 乙种货车/辆 总量(吨)
第一次 4 5 31
第二次 3 6 30
(1)甲、乙两种货车满载时每辆分别能运输原料多少吨?
(2)该公司又新购买45吨原料,准备同时租用这两种货车,每辆均全部装满,问有哪几种租车方案?
(3)在(2)的前提下,已知甲种货车每辆租金为300元,乙种货车每辆租金为200元,选择哪种租车方案最省钱?
28.(10分)已知AB∥CD,点E在直线AB,CD之间,连接AE,CE.
(1)如图1,求证:∠BAE+∠DCE=∠AEC;
(2)若AH平分∠BAE,将线段CE沿CD方向平移至FG(CE∥FG).
①如图2,若∠AEC=80°,FH平分∠DFG,求∠AHF的度数;
②如图3,若FH平分∠CFG,请写出∠AHF与∠AEC的数量关系,并说明理由.
29.(10分)已知△ABC是等边三角形,点D为射线BC上一动点,连接AD,以AD为边在直线AD右侧作等边△ADE.
(1)如图1,点D在线段BC上,连接CE,若AB=4,且CE=1,求线段AD的长;
(2)如图2,点D是BC延长线上一点,过点E作EF⊥AC于点F,求证:CF=AF+CD;
(3)如图3,若AB=8,点D在射线BC上运动,取AC中点G,连接EG,请直接写出EG的最小值.
2024-2025学年山东省淄博市博山区七年级(下)期末数学试卷(五四学制)
参考答案与试题解析
一.选择题(共12小题)
题号 1 2 3 4 5 6 7 8 9 10 11
答案 C B B D D C A B A B A
题号 12
答案 B
二、填空题:本大题共10个小题,每小题4分,共40分。
13.解:选中“红叶柿岩”的概率是:,
故答案为:.
14.解:过点E作AB∥EO,如图:
∵AB∥EO,∠ABE=50°,
∴∠ABE=∠BEO=50°(两直线平行,内错角相等),
∵AB∥CD,
∴CD∥EO,
∵∠CDE=35°,
∴∠OED=∠CDE=35°(两直线平行,内错角相等),
∴∠BED=∠BEO+∠OED=50°+35°=85°,
故答案为:85°.
15.解:∵(a+2)x|a|﹣1+y=5是一个二元一次方程,
∴,
解得:a=2,
故答案为:2.
16.解:∵△ABC≌△DEF,BC=5cm,BF=7cm,
∴BC=EF=5cm,
∴FC=BE=BF﹣BC=2cm,
∴EC=BC﹣BE=5﹣2=3(cm).
故答案为:3cm.
17.解:,
①+②,得2x+2y=3k,即,
∵x+y=3,
∴,
去分母,得3k=6,
解得:k=2.
故答案为:2.
18.解:①垂线段最短,正确,是真命题,符合题意;
②两条平行直线被第三条直线所截,内错角相等,故原命题错误,是假命题,不符合题意;
③互补的角不一定是邻补角,故原命题错误,是假命题,不符合题意;
④同旁内角互补,两直线平行,故原命题错误,是假命题,不符合题意.
真命题是①,
故答案为:①.
19.解:根据作图痕迹可知:射线OP是∠AOB的角平分线,∠AOB=60°,ED是线段OC的垂直平分线,
∴PD⊥OC,,
∵PD=3cm,
∴OP=2PD=6cm,
∵∠AOB=60°,
∴∠OED=90°﹣60°=30°=∠EOP,
∴PE=PO=6cm.
故答案为:6.
20.解:解不等式得x<3,
解不等式2x﹣5<3x﹣a得x>a﹣5,
∵不等式有5个整数解,
∴不等式的整数解是2,1,0,﹣1,﹣2,
∴﹣3≤a﹣5<﹣2,
∴2≤a<3.
故答案为:2≤a<3.
21.解:设EF交AC于点H,
∵把四边形ABED沿直线DE折叠得到四边形GFED,
∴∠G=∠A,∠F=∠B,∠DEF=∠DEB,
∵∠DEF=α,∠C=β,
∴∠BEF=2∠DEF=2α,
∴∠CEH=180°﹣2α,
∵GF∥AC,
∴∠F=∠CHF=∠CEH+∠C=180°﹣2α+β,
∴∠B=180°﹣2α+β,
∴∠G=∠A=180°﹣(∠B+∠C)=180°﹣(180°﹣2α+β+β)=2α﹣2β,
故答案为:2α﹣2β.
22.解:设这列数中0的个数为x,﹣2的个数为y,
则1的个数为(2025﹣x﹣y)个,
因为a1+a2+ +a2024+a2025=950,(a1+1)2+(a2+1)2+...+(a2024+1)2+(a2025+1)2=5025,
所以,
解得,
所以这列数中0的个数为1000个.
故答案为:1000.
三、解答题:本大题共7个小题,共62分。解答要写出必要的文字说明、证明过程或演算步骤。
23.解:,
解不等式①得:x≥﹣1,
解不等式②得:x<4,
故原不等式组的解集为:﹣1≤x<4,
在数轴上表示为:
24.证明:∵点B为线段AC的中点,
∴AB=BC,
∵AD∥BE,
∴∠A=∠EBC,
∵BD∥CE,
∴∠C=∠DBA,
在△ABD与△BCE中,
,
∴△ABD≌△BCE.(ASA).
25.解:(1)∵甲顾客购物150元,
∴可以获得一次转动转盘的机会,
∵黄色区域一共有2个,
∴他得到50元的购物券的概率是;
(2)∵红色、黄色、绿色区域一共有7个,
∴他获得购物券的概率是;
(3)如图所示:
游戏规则:把转盘被等分成8个扇形,其中红色、黄色、绿色区域各一个,如果转盘停止后,指针正好对准红、黄或绿色区域,顾客就可以分别获得100元,50元,20元的购物券,则顾客获得购物券的概率是.
26.(1)证明:∵DG∥BC,
∴∠1=∠DCB,
∵∠1=∠2,
∴∠2=∠DCB,
∴DC∥EF.
(2)解:∵EF⊥AB,
∴∠FEB=90°,
∵∠1=∠2=55°,
∴∠B=90°﹣55°=35°,
∵DG∥BC,
∴∠ADG=∠B=35°.
27.解:(1)设甲种货车每辆能装货x吨,乙种货车每辆能装货y吨,
依题意有:,
解得:,
答:甲种货车每辆能装货4吨,乙种货车每辆能装货3吨;
(2)设租用甲种货车m辆,乙种货车n辆,
依题意有:4m+3n=45,
∴.
∵m,n均为正整数,
∴或 或,
∴共有3种租车方案,
方案1:租用9辆甲种货车,3辆乙种货车;
方案2:租用6辆甲种货车,7辆乙种货车;
方案3:租用3辆甲种货车,11辆乙种货车.
(3)方案1所需费用:300×9+200×3=3300(元);
方案2所需费用:300×6+200×7=3200(元);
方案3所需费用:300×3+200×11=3100(元).
∵3300>3200>3100,
∴方案3所需费用最少,最少费用是3100元.
28.解:(1)如图1中,
过E作EF∥AB,
∵AB∥CD,
∴EF∥CD,
∴∠BAE=∠AEF,∠DCE=∠CEF,
∴∠AEC=∠AEF+∠CEF=∠BAE=∠DCE,
∴∠BAE+∠DCE=∠AEC;
(2)①如图2中,
∵FG∥CE,
∴∠ECD=∠GFD,
∵AH平分∠BAE,HF平分∠GFD,
∴∠BAH∠BAE,∠DFH∠DFG∠DCE,
∴∠AHF=∠BAH+∠DFH(∠BAE+∠DCE),
∵∠BAE+∠DCE=∠AEC=80°,
∴∠AHF80°=40°.
②如图3中,结论:∠AHF=90°∠AEC.
理由:∵∠AHF=∠BAH+∠HFD,∠BAH∠BAE,∠GFH(180°﹣∠DFG),∠ECD=∠DFG,
∴∠AHF∠BAE+90°∠DFG+∠DFG=90°(∠BAE+∠DCE)=90°∠AEC.
29.(1)解:∵△ABC和△ADE是等边三角形,
∴AB=AC,∠BAC=∠B=∠ACB=∠DAE=60°,AD=AE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
即∠BAD=∠CAE,
∴△ABD≌△ACE (SAS),
∴BD=CE=1,
如图1,过点D作DM⊥AB于点M,
则∠DMB=∠DMA=90°,
∴∠BDM=90°﹣∠B=90°﹣60°=30°,
∴BMBD,
∴AM=AB﹣BM=4,
∴DM,
∴AD,
即AD的长为;
(2)证明:如图2,在CA上截取CH=CD,连接EH,
∵△ABC和△ADE是等边三角形,
∴AB=AC,∠BAC=∠B=∠ACB=∠DAE=60°,AD=AE=DE,
∴∠BAC+∠DAC=∠DAE+∠DAC,
即∠BAD=∠CAE,
∴△ABD≌△ACE (SAS),
∴∠B=∠ACE=60°,
∴∠DCE=180°﹣∠ACB﹣∠ACE=180°﹣60°﹣60°=60°,
∴∠HCE=∠DCE,
∵CH=CD,CE=CE,
∴△HCE≌△DCE(SAS),
∴HE=DE,
∴AE=HE,
∵EF⊥AC,
∴∠EFA=∠EFH=90°,
又∵EF=EF,
∴Rt△AEF≌Rt△HEF(HL),
∴AF=HF,
∵CF=HF+CH,
∴CF=AF+CD;
(3)解:如图3,连接CE,延长BC至点P,
∵△ABC是等边三角形,
∴AC=AB=8,∠B=∠ACB=60°,
∴∠ACP=120°,
同(1)得:△ABD≌△ACE(SAS),
∴∠ACE=∠B=60°,
∴∠ACE∠ACP,
∴点E在△ABC的外角∠ACP的角平分线上运动,
由垂线段最短可知,当EG⊥CE时,EG最短,
∵点G是AC的中点,
∴CGAC=4,
∵∠ACE=60°,∠GEC=90°,
∴∠CGE=30°,
∴CECG=2,
∴EG2,
即EG的最小值为2.
第1页(共1页)
一、选择题:本大题共12个小题,每小题4分,共48分。在每小题所给出的四个选项中,只有一项是符合题目要求的。
1.(4分)下列解集中,包括2的是( )
A.x<2 B.x≥3 C.x≤3 D.x>2
2.(4分)掷一枚质地均匀的骰子2次,向上一面的点数和是13.这个事件是( )
A.随机事件 B.不可能事件
C.必然事件 D.无法确定
3.(4分)如图:在△ABC中,AB=AC,BD平分∠ABC,交AC于点D,若BD=BC,则∠A等于( )
A.30° B.36° C.40° D.42°
4.(4分)若是方程3x﹣ay=4的一个解,则a的值为( )
A.1 B.﹣1 C.3 D.2
5.(4分)判断命题“对任意实数a,都有(a+1)2>0”是假命题,只需要举出反例,反例中a的可以是( )
A.2 B.1 C.0 D.﹣1
6.(4分)如图,下列条件中,不能判断c∥d的是( )
A.∠1=∠2 B.∠3+∠5=180°
C.∠2+∠5=180° D.∠4=∠5
7.(4分)运行程序如图所示,规定:从“输入一个值x”到“结果是否>95”为一次程序操作,如果程序操作运行了两次就停止,那么x的取值范围是( )
A.23<x≤47 B.11<x≤23 C.7<x≤11 D.3<x≤7
8.(4分)如图1所示,是地理学科实践课上第一小组同学在一张面积为36cm2的长方形卡纸上绘制的山东省政区图(图中阴影部分),他们想了解该图案的面积是多少,经研究采取了以下办法:将长方形卡纸水平放置在地面上,在适当位置随机地朝长方形区域扔小球,并记录小球落在不规则图案上的次数(球扔在界线上或长方形区域外不计试验结果).他们将若干次有效试验的结果绘制成了如图2所示的统计图,由此估计不规则图案的面积大约为( )
A.55.38cm2 B.23.4cm2 C.25.2cm2 D.24.28cm2
9.(4分)如图,一次函数yx的图象与y=kx+7的图象相交于点A,则方程组的解是( )
A. B. C. D.
10.(4分)立定跳远动作中,从起跳到落地瞬间的几个身体相关关节的角度,对跳远成绩起着举足轻重的作用.如图是小李落地瞬间的动作及其示意图,若AG∥CD,∠BCD=74°,∠B=44°,则∠BAG的度数为( )
A.26° B.30° C.34° D.40°
11.(4分)若一个长方形可以分割为几个大小不同的小正方形,则称这个长方形为完美长方形,1925年数学家莫伦发现了第一个完美长方形,它被分割成9个大小不同的正方形,已知最小正方形的周长为8,则最大正方形A的面积为( )
A.1296 B.1444 C.2304 D.20736
12.(4分)如图,在△ABC中,∠ACB=90°,AC=BC,AD平分∠BAC,CE⊥AD交AB于E,点G是AD上的一点,且∠ACG=45°,连BG交CE于P,连DP,下列结论:①AC=AE;
②CD=BE;
③BG+2DP=AD;
④PG=PE.
其中正确的有( )
A.①②③ B.①②④ C.①③④ D.①②③④
二、填空题:本大题共10个小题,每小题4分,共40分。
13.(4分)暑假期间,小明打算在“红叶柿岩”“陶琉大观园”“石门风景区”“原山国家森林公园”“鲁山国家森林公园”这五个景点中随机选择一个去游玩,恰好选中“红叶柿岩”的概率是 .
14.(4分)如图,平行光线AB和CD经过凹面镜反射后汇聚于点E,若∠ABE=50°,∠CDE=35°,则∠BED的度数是 .
15.(4分)已知(a+2)x|a|﹣1+y=5是二元一次方程,则a的值为 .
16.(4分)如图,△ABC≌△DEF.若BC=5cm,BF=7cm,则EC的长是 .
17.(4分)若关于x,y的二元一次方程组的解也是二元一次方程x+y=3的解,则k= .
18.(4分)给出如下列4个命题,其中是真命题的是 .(请填写命题的序号)
①垂线段最短;②两条直线被第三条直线所截,内错角相等;③互补的角是邻补角;④同旁内角相等,两直线平行.
19.(4分)如图所示,为尺规作图痕迹,若∠AOB=60°,PD=3cm,则PE长为 cm.
20.(4分)已知关于x的不等式组有5个整数解,则a的取值范围是 .
21.(4分)如图,在△ABC中,D、E分别是AC、BC上的点,把四边形ABED沿直线DE折叠得到四边形GFED,GF∥AC,若∠DEF=α,∠C=β,则∠G= .(用含α、β的式子表示)
22.(4分)设a1,a2, ,a2024,a2025是从﹣2,0,1这三个数取值的一组数,若a1+a2+ +a2024+a2025=950,(a1+1)2+(a2+1)2+ +(a2024+1)2+(a2025+1)2=5025,则a1,a2, ,a2024,a2025中为0的个数为 个.
三、解答题:本大题共7个小题,共62分。解答要写出必要的文字说明、证明过程或演算步骤。
23.(8分)解不等式组,并把解集在数轴上表示出来.
24.(8分)如图,B是线段AC的中点,AD∥BE,BD∥CE.求证:△ABD≌△BCE.
25.(8分)在五一期间,某商场为了吸引顾客,设立了一个可以自由转动的转盘(如图1),并规定:顾客每购买100元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红、黄或绿色区域,顾客就可以分别获得100元,50元,20元的购物券(转盘被等分成20个扇形).已知甲顾客购物150元.
(1)他得到50元的购物券的概率是多少?
(2)他获得购物券的概率是多少?
(3)请你利用图2所示转盘,设计一个转盘游戏,使得顾客获得购物券的概率是,并简要说明游戏规则.
26.(8分)如图,点D、E在AB上,点F、G分别在BC、CA上,且DG∥BC,∠1=∠2.
(1)求证:DC∥EF;
(2)若EF⊥AB,∠1=55°,求∠ADG的度数.
27.(10分)某公司用甲、乙两种货车运输原料,两次满载的运输情况如表:
甲种货车/辆 乙种货车/辆 总量(吨)
第一次 4 5 31
第二次 3 6 30
(1)甲、乙两种货车满载时每辆分别能运输原料多少吨?
(2)该公司又新购买45吨原料,准备同时租用这两种货车,每辆均全部装满,问有哪几种租车方案?
(3)在(2)的前提下,已知甲种货车每辆租金为300元,乙种货车每辆租金为200元,选择哪种租车方案最省钱?
28.(10分)已知AB∥CD,点E在直线AB,CD之间,连接AE,CE.
(1)如图1,求证:∠BAE+∠DCE=∠AEC;
(2)若AH平分∠BAE,将线段CE沿CD方向平移至FG(CE∥FG).
①如图2,若∠AEC=80°,FH平分∠DFG,求∠AHF的度数;
②如图3,若FH平分∠CFG,请写出∠AHF与∠AEC的数量关系,并说明理由.
29.(10分)已知△ABC是等边三角形,点D为射线BC上一动点,连接AD,以AD为边在直线AD右侧作等边△ADE.
(1)如图1,点D在线段BC上,连接CE,若AB=4,且CE=1,求线段AD的长;
(2)如图2,点D是BC延长线上一点,过点E作EF⊥AC于点F,求证:CF=AF+CD;
(3)如图3,若AB=8,点D在射线BC上运动,取AC中点G,连接EG,请直接写出EG的最小值.
2024-2025学年山东省淄博市博山区七年级(下)期末数学试卷(五四学制)
参考答案与试题解析
一.选择题(共12小题)
题号 1 2 3 4 5 6 7 8 9 10 11
答案 C B B D D C A B A B A
题号 12
答案 B
二、填空题:本大题共10个小题,每小题4分,共40分。
13.解:选中“红叶柿岩”的概率是:,
故答案为:.
14.解:过点E作AB∥EO,如图:
∵AB∥EO,∠ABE=50°,
∴∠ABE=∠BEO=50°(两直线平行,内错角相等),
∵AB∥CD,
∴CD∥EO,
∵∠CDE=35°,
∴∠OED=∠CDE=35°(两直线平行,内错角相等),
∴∠BED=∠BEO+∠OED=50°+35°=85°,
故答案为:85°.
15.解:∵(a+2)x|a|﹣1+y=5是一个二元一次方程,
∴,
解得:a=2,
故答案为:2.
16.解:∵△ABC≌△DEF,BC=5cm,BF=7cm,
∴BC=EF=5cm,
∴FC=BE=BF﹣BC=2cm,
∴EC=BC﹣BE=5﹣2=3(cm).
故答案为:3cm.
17.解:,
①+②,得2x+2y=3k,即,
∵x+y=3,
∴,
去分母,得3k=6,
解得:k=2.
故答案为:2.
18.解:①垂线段最短,正确,是真命题,符合题意;
②两条平行直线被第三条直线所截,内错角相等,故原命题错误,是假命题,不符合题意;
③互补的角不一定是邻补角,故原命题错误,是假命题,不符合题意;
④同旁内角互补,两直线平行,故原命题错误,是假命题,不符合题意.
真命题是①,
故答案为:①.
19.解:根据作图痕迹可知:射线OP是∠AOB的角平分线,∠AOB=60°,ED是线段OC的垂直平分线,
∴PD⊥OC,,
∵PD=3cm,
∴OP=2PD=6cm,
∵∠AOB=60°,
∴∠OED=90°﹣60°=30°=∠EOP,
∴PE=PO=6cm.
故答案为:6.
20.解:解不等式得x<3,
解不等式2x﹣5<3x﹣a得x>a﹣5,
∵不等式有5个整数解,
∴不等式的整数解是2,1,0,﹣1,﹣2,
∴﹣3≤a﹣5<﹣2,
∴2≤a<3.
故答案为:2≤a<3.
21.解:设EF交AC于点H,
∵把四边形ABED沿直线DE折叠得到四边形GFED,
∴∠G=∠A,∠F=∠B,∠DEF=∠DEB,
∵∠DEF=α,∠C=β,
∴∠BEF=2∠DEF=2α,
∴∠CEH=180°﹣2α,
∵GF∥AC,
∴∠F=∠CHF=∠CEH+∠C=180°﹣2α+β,
∴∠B=180°﹣2α+β,
∴∠G=∠A=180°﹣(∠B+∠C)=180°﹣(180°﹣2α+β+β)=2α﹣2β,
故答案为:2α﹣2β.
22.解:设这列数中0的个数为x,﹣2的个数为y,
则1的个数为(2025﹣x﹣y)个,
因为a1+a2+ +a2024+a2025=950,(a1+1)2+(a2+1)2+...+(a2024+1)2+(a2025+1)2=5025,
所以,
解得,
所以这列数中0的个数为1000个.
故答案为:1000.
三、解答题:本大题共7个小题,共62分。解答要写出必要的文字说明、证明过程或演算步骤。
23.解:,
解不等式①得:x≥﹣1,
解不等式②得:x<4,
故原不等式组的解集为:﹣1≤x<4,
在数轴上表示为:
24.证明:∵点B为线段AC的中点,
∴AB=BC,
∵AD∥BE,
∴∠A=∠EBC,
∵BD∥CE,
∴∠C=∠DBA,
在△ABD与△BCE中,
,
∴△ABD≌△BCE.(ASA).
25.解:(1)∵甲顾客购物150元,
∴可以获得一次转动转盘的机会,
∵黄色区域一共有2个,
∴他得到50元的购物券的概率是;
(2)∵红色、黄色、绿色区域一共有7个,
∴他获得购物券的概率是;
(3)如图所示:
游戏规则:把转盘被等分成8个扇形,其中红色、黄色、绿色区域各一个,如果转盘停止后,指针正好对准红、黄或绿色区域,顾客就可以分别获得100元,50元,20元的购物券,则顾客获得购物券的概率是.
26.(1)证明:∵DG∥BC,
∴∠1=∠DCB,
∵∠1=∠2,
∴∠2=∠DCB,
∴DC∥EF.
(2)解:∵EF⊥AB,
∴∠FEB=90°,
∵∠1=∠2=55°,
∴∠B=90°﹣55°=35°,
∵DG∥BC,
∴∠ADG=∠B=35°.
27.解:(1)设甲种货车每辆能装货x吨,乙种货车每辆能装货y吨,
依题意有:,
解得:,
答:甲种货车每辆能装货4吨,乙种货车每辆能装货3吨;
(2)设租用甲种货车m辆,乙种货车n辆,
依题意有:4m+3n=45,
∴.
∵m,n均为正整数,
∴或 或,
∴共有3种租车方案,
方案1:租用9辆甲种货车,3辆乙种货车;
方案2:租用6辆甲种货车,7辆乙种货车;
方案3:租用3辆甲种货车,11辆乙种货车.
(3)方案1所需费用:300×9+200×3=3300(元);
方案2所需费用:300×6+200×7=3200(元);
方案3所需费用:300×3+200×11=3100(元).
∵3300>3200>3100,
∴方案3所需费用最少,最少费用是3100元.
28.解:(1)如图1中,
过E作EF∥AB,
∵AB∥CD,
∴EF∥CD,
∴∠BAE=∠AEF,∠DCE=∠CEF,
∴∠AEC=∠AEF+∠CEF=∠BAE=∠DCE,
∴∠BAE+∠DCE=∠AEC;
(2)①如图2中,
∵FG∥CE,
∴∠ECD=∠GFD,
∵AH平分∠BAE,HF平分∠GFD,
∴∠BAH∠BAE,∠DFH∠DFG∠DCE,
∴∠AHF=∠BAH+∠DFH(∠BAE+∠DCE),
∵∠BAE+∠DCE=∠AEC=80°,
∴∠AHF80°=40°.
②如图3中,结论:∠AHF=90°∠AEC.
理由:∵∠AHF=∠BAH+∠HFD,∠BAH∠BAE,∠GFH(180°﹣∠DFG),∠ECD=∠DFG,
∴∠AHF∠BAE+90°∠DFG+∠DFG=90°(∠BAE+∠DCE)=90°∠AEC.
29.(1)解:∵△ABC和△ADE是等边三角形,
∴AB=AC,∠BAC=∠B=∠ACB=∠DAE=60°,AD=AE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
即∠BAD=∠CAE,
∴△ABD≌△ACE (SAS),
∴BD=CE=1,
如图1,过点D作DM⊥AB于点M,
则∠DMB=∠DMA=90°,
∴∠BDM=90°﹣∠B=90°﹣60°=30°,
∴BMBD,
∴AM=AB﹣BM=4,
∴DM,
∴AD,
即AD的长为;
(2)证明:如图2,在CA上截取CH=CD,连接EH,
∵△ABC和△ADE是等边三角形,
∴AB=AC,∠BAC=∠B=∠ACB=∠DAE=60°,AD=AE=DE,
∴∠BAC+∠DAC=∠DAE+∠DAC,
即∠BAD=∠CAE,
∴△ABD≌△ACE (SAS),
∴∠B=∠ACE=60°,
∴∠DCE=180°﹣∠ACB﹣∠ACE=180°﹣60°﹣60°=60°,
∴∠HCE=∠DCE,
∵CH=CD,CE=CE,
∴△HCE≌△DCE(SAS),
∴HE=DE,
∴AE=HE,
∵EF⊥AC,
∴∠EFA=∠EFH=90°,
又∵EF=EF,
∴Rt△AEF≌Rt△HEF(HL),
∴AF=HF,
∵CF=HF+CH,
∴CF=AF+CD;
(3)解:如图3,连接CE,延长BC至点P,
∵△ABC是等边三角形,
∴AC=AB=8,∠B=∠ACB=60°,
∴∠ACP=120°,
同(1)得:△ABD≌△ACE(SAS),
∴∠ACE=∠B=60°,
∴∠ACE∠ACP,
∴点E在△ABC的外角∠ACP的角平分线上运动,
由垂线段最短可知,当EG⊥CE时,EG最短,
∵点G是AC的中点,
∴CGAC=4,
∵∠ACE=60°,∠GEC=90°,
∴∠CGE=30°,
∴CECG=2,
∴EG2,
即EG的最小值为2.
第1页(共1页)
同课章节目录
