1.1 空间几何体的结构特征 学案1(无答案)
文档属性
| 名称 | 1.1 空间几何体的结构特征 学案1(无答案) | 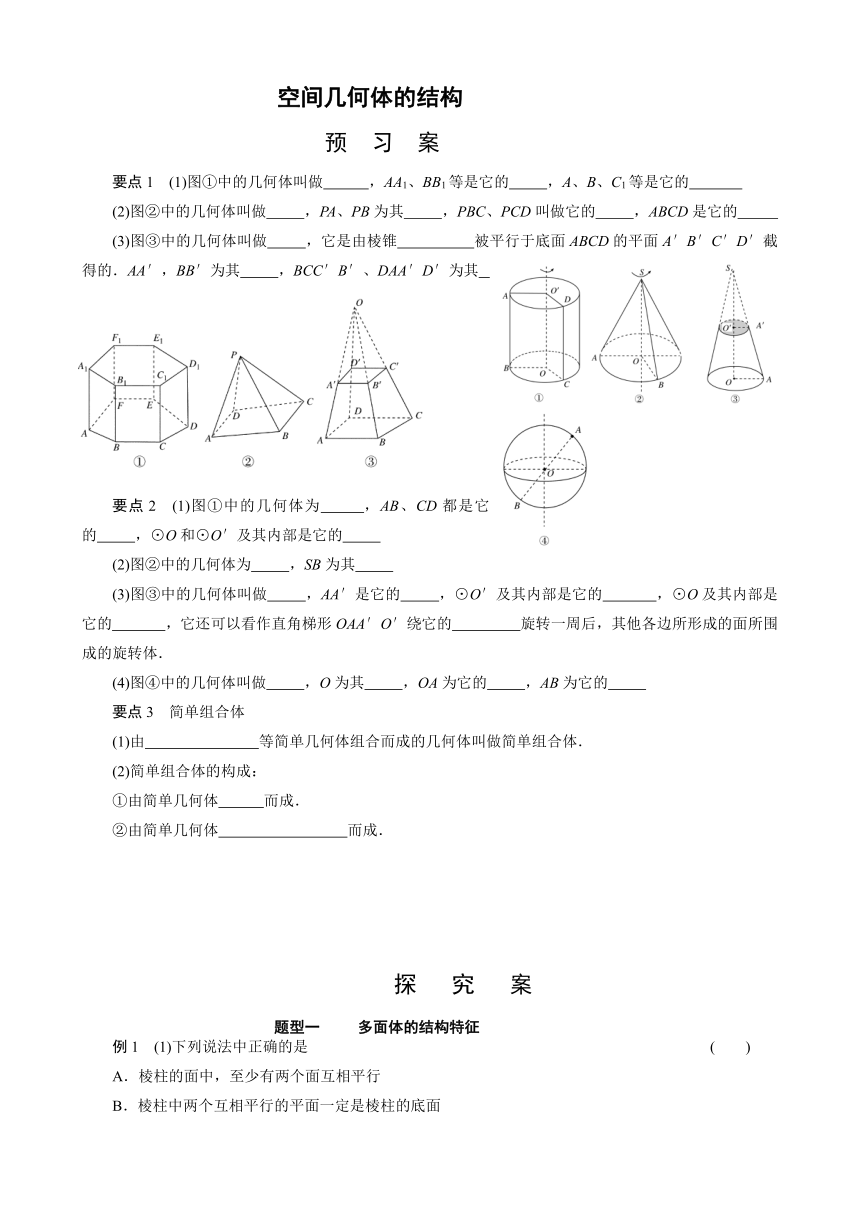 | |
| 格式 | zip | ||
| 文件大小 | 165.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-08-02 20:22:26 | ||
图片预览

文档简介
空间几何体的结构
预
习
案
要点1 (1)图①中的几何体叫做
,AA1、BB1等是它的
,A、B、C1等是它的
(2)图②中的几何体叫做
,PA、PB为其
,PBC、PCD叫做它的
,ABCD是它的
(3)图③中的几何体叫做
,它是由棱锥
被平行于底面ABCD的平面A′B′C′D′截得的.AA′,BB′为其
,BCC′B′、DAA′D′为其
要点2 (1)图①中的几何体为
,AB、CD都是它的
,⊙O和⊙O′及其内部是它的
(2)图②中的几何体为
,SB为其
(3)图③中的几何体叫做
,AA′是它的
,⊙O′及其内部是它的
,⊙O及其内部是它的
,它还可以看作直角梯形OAA′O′绕它的
旋转一周后,其他各边所形成的面所围成的旋转体.
(4)图④中的几何体叫做
,O为其
,OA为它的
,AB为它的
要点3 简单组合体
(1)由
等简单几何体组合而成的几何体叫做简单组合体.
(2)简单组合体的构成:
①由简单几何体
而成.
②由简单几何体
而成.
探
究
案
题型一
多面体的结构特征
例1 (1)下列说法中正确的是
( )
A.棱柱的面中,至少有两个面互相平行
B.棱柱中两个互相平行的平面一定是棱柱的底面
C.棱柱中一条侧棱的长叫作棱柱的高
D.棱柱的侧面是平行四边形,但它的底面一定不是平行四边形
例2 下列结论正确的有________.
①棱锥中至少有三个面是三角形;
②棱锥的侧棱长与底面多边形的边长相等,则该棱锥可能是六棱锥;
③棱台的两底面相似;
④棱台的侧面都是梯形且侧棱都相等.
探究2 棱柱、棱锥、棱台的结构特征
底面
侧面
侧棱
棱柱
平行且相等的多边形
平行四边形
平行且相等
棱台
平行且相似的多边形
梯形
延长后交于一点
棱锥
多边形
三角形
交于一点
题型二
圆柱、圆锥、圆台的结构特征
例3 下列叙述正确的个数是
( )
(1)以直角三角形的一边为轴旋转所得的旋转体是圆锥;
(2)以直角梯形的一腰为轴旋转所得的几何体是圆台;
(3)圆柱、圆锥、圆台的底面都是圆;
(4)用一个平面去截圆锥,得到一个圆锥和一个圆台.
A.0
B.1
C.2
D.3
探究3 圆柱、圆锥、圆台的结构特征
底面
侧面
母线
圆柱
平行且相等的圆
曲面
平行且相等
圆台
平行且相似的圆
曲面
延长交于一点
圆锥
圆
曲面
交于一点
例4 判断下列说法是否正确,并说明理由.
①空间中到定点的距离等于定长r的点的集合,构成半径为r的球.
②空间中到定点的距离等于定长r的点的集合,构成半径为r的球面.
③一个圆绕其直径旋转半周所形成的曲面围成的几何体是球.
④球的对称轴有无数条,对称中心也有无数个.
⑤用平面截球,随着平面角度不同,截面可能不是圆面.
题型三
组合体
例1 观察下图中的几何体,分析它们是由哪些基本几何体组成的.
题型四
展开与折叠
例2 如图是三个几何体的表面展开图,请问各是什么几何体?
预
习
案
要点1 (1)图①中的几何体叫做
,AA1、BB1等是它的
,A、B、C1等是它的
(2)图②中的几何体叫做
,PA、PB为其
,PBC、PCD叫做它的
,ABCD是它的
(3)图③中的几何体叫做
,它是由棱锥
被平行于底面ABCD的平面A′B′C′D′截得的.AA′,BB′为其
,BCC′B′、DAA′D′为其
要点2 (1)图①中的几何体为
,AB、CD都是它的
,⊙O和⊙O′及其内部是它的
(2)图②中的几何体为
,SB为其
(3)图③中的几何体叫做
,AA′是它的
,⊙O′及其内部是它的
,⊙O及其内部是它的
,它还可以看作直角梯形OAA′O′绕它的
旋转一周后,其他各边所形成的面所围成的旋转体.
(4)图④中的几何体叫做
,O为其
,OA为它的
,AB为它的
要点3 简单组合体
(1)由
等简单几何体组合而成的几何体叫做简单组合体.
(2)简单组合体的构成:
①由简单几何体
而成.
②由简单几何体
而成.
探
究
案
题型一
多面体的结构特征
例1 (1)下列说法中正确的是
( )
A.棱柱的面中,至少有两个面互相平行
B.棱柱中两个互相平行的平面一定是棱柱的底面
C.棱柱中一条侧棱的长叫作棱柱的高
D.棱柱的侧面是平行四边形,但它的底面一定不是平行四边形
例2 下列结论正确的有________.
①棱锥中至少有三个面是三角形;
②棱锥的侧棱长与底面多边形的边长相等,则该棱锥可能是六棱锥;
③棱台的两底面相似;
④棱台的侧面都是梯形且侧棱都相等.
探究2 棱柱、棱锥、棱台的结构特征
底面
侧面
侧棱
棱柱
平行且相等的多边形
平行四边形
平行且相等
棱台
平行且相似的多边形
梯形
延长后交于一点
棱锥
多边形
三角形
交于一点
题型二
圆柱、圆锥、圆台的结构特征
例3 下列叙述正确的个数是
( )
(1)以直角三角形的一边为轴旋转所得的旋转体是圆锥;
(2)以直角梯形的一腰为轴旋转所得的几何体是圆台;
(3)圆柱、圆锥、圆台的底面都是圆;
(4)用一个平面去截圆锥,得到一个圆锥和一个圆台.
A.0
B.1
C.2
D.3
探究3 圆柱、圆锥、圆台的结构特征
底面
侧面
母线
圆柱
平行且相等的圆
曲面
平行且相等
圆台
平行且相似的圆
曲面
延长交于一点
圆锥
圆
曲面
交于一点
例4 判断下列说法是否正确,并说明理由.
①空间中到定点的距离等于定长r的点的集合,构成半径为r的球.
②空间中到定点的距离等于定长r的点的集合,构成半径为r的球面.
③一个圆绕其直径旋转半周所形成的曲面围成的几何体是球.
④球的对称轴有无数条,对称中心也有无数个.
⑤用平面截球,随着平面角度不同,截面可能不是圆面.
题型三
组合体
例1 观察下图中的几何体,分析它们是由哪些基本几何体组成的.
题型四
展开与折叠
例2 如图是三个几何体的表面展开图,请问各是什么几何体?
