1.2 空间几何体的三视图和直观图 学案(含答案)
文档属性
| 名称 | 1.2 空间几何体的三视图和直观图 学案(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 234.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-08-02 00:00:00 | ||
图片预览


文档简介
1.2空间几何体的三视图和直观图
1.2.1中心投影与平行投影
1.2.2空间几何体的三视图
【考纲要求】
[学习目标]
1.了解中心投影和平行投影.
2.能画出简单空间图形(柱、锥、台、球及其组合体)的三视图.
3.能识别三视图所表示的立体模型.
[目标解读]
1.会画简单空间图形的三视图是重点;
2.识别三视图所表示的立体模型是难点.
【自主学习】
1.投影
(1)投影的定义
由于光的照射,在
物体后面
( http: / / www.21cnjy.com )的屏幕上可以留下这个物体的
,这种现象叫做投影.其中,我们把
叫做投影线,把
的屏幕叫做投影面.
(2)投影的分类
①中心投影:光由
散射形成的投影.
②平行投影:在一束
照射下形成的投影.
当投影线
时,叫做正投影,否则叫做
.
(3)投影的性质
①中心投影的性质:中心投影的
交于一点;当光源距离物体越近,投影形成的影子
.
②平行投影的性质:平行投影的投影线
.
2.三视图
(1)分类
①正视图:光线从几何体的
向
正投影,得到的投影图;
②侧视图:光线从几何体的
向
正投影,得到的投影图;
③俯视图:光线从几何体的
向
正投影,得到的投影图.
(2)三视图的画法规则
①
视图都反映物体的长度——“长对正”;
②
视图都反映物体的高度——“高平齐”;
③
视图都反映物体的宽度——“宽相等”.
特别提醒:画几何体的三视图时,能看见的轮廓线和棱用实线表示,不能看见的轮廓线和棱用虚线表示.
【考点突破】
要点一
平行投影与中心投影
中心投影与平行投影都是空间图形的基本画法,
( http: / / www.21cnjy.com )是投影的两种形式.通过中心投影与平行投影将三维物体转换成二维平面物体,可以通过投影想象实际物体的形状,但还不能完全反映真实情况,只能反映部分形状,只有在特殊情况下反映真实尺寸.
画立体几何图形时一般采用平行投影法,画实际
( http: / / www.21cnjy.com )效果图时采用中心投影法,中心投影的投影线交于一点,点光源离物体越近,投影形成的影子越大;平行投影的投影线是平行的.
典型例题1、在正方体ABCD-A′B′C′D′中,E、F分别是A′A、C′C的中点,则下列判断正确的是________.
①四边形BFD′E在底面ABCD内的投影是正方形
②四边形BFD′E在面A′D′DA内的投影是菱形
③四边形BFD′E在面A′D′DA内的投影与在面ABB′A′内的投影是全等的平行四边形
【思路启迪】 先根据平行投影的定义知投影线垂直于投影面,从而确定四边形BFD′E四点在各投影面的位置.再把各投影点连线成图.
【解析】 ①四边形BFD′E的四个顶点在底面ABCD内的投影分别是点B、C、D、A,故投影是正方形,正确;
②设正方体的边长为2,则A
( http: / / www.21cnjy.com )E=1,取D′D的中点G,则四边形BFD′E在面A′D′DA内的投影是四边形AGD′E,由AE∥D′G,且AE=D′G,∴四边形AGD′E是平行四边形.但AE=1,D′E=,故四边形AGD′E不是菱形.对于③,由②知是两个边长分别相等的平行四边形,从而③正确.
方法指导:画出一个图形在一个投影面上的
( http: / / www.21cnjy.com )投影的关键是确定该图形的关键点(如顶点,端点等),先画出这些关键点的投影,再依次连接即可得此图形在投影面上的投影.
反馈训练1、如图甲所示,在正方体A
( http: / / www.21cnjy.com )BCD-A1B1C1D1中,E、F分别是AA1、C1D1的中点,G是正方形BCC1B1的中心,则四边形AGFE在该正方体的各个面上的投影可能是图乙中的________.
要点二
画空间几何体的三视图
1.三视图是用两两相互垂直的三个平
( http: / / www.21cnjy.com )面(正面、侧面、水平面)作为投影面,把物体放在这个空间内,分别向三个平面进行正投影,然后将水平投影绕水平面和正面的交线向下转90°,将侧面投影绕侧面和正面的交线向右转90°,就得到了三视图,即画出的三视图需要符合长对正、高平齐、宽相等的基本特征.
2.画简单组合体的三视图时,先要分析该组合体
( http: / / www.21cnjy.com )的结构特征,再想象模型,从正前方、左方、正上方三个不同角度各能看到什么形状,再借助简单几何体的三视图,画出简单组合体的三视图.
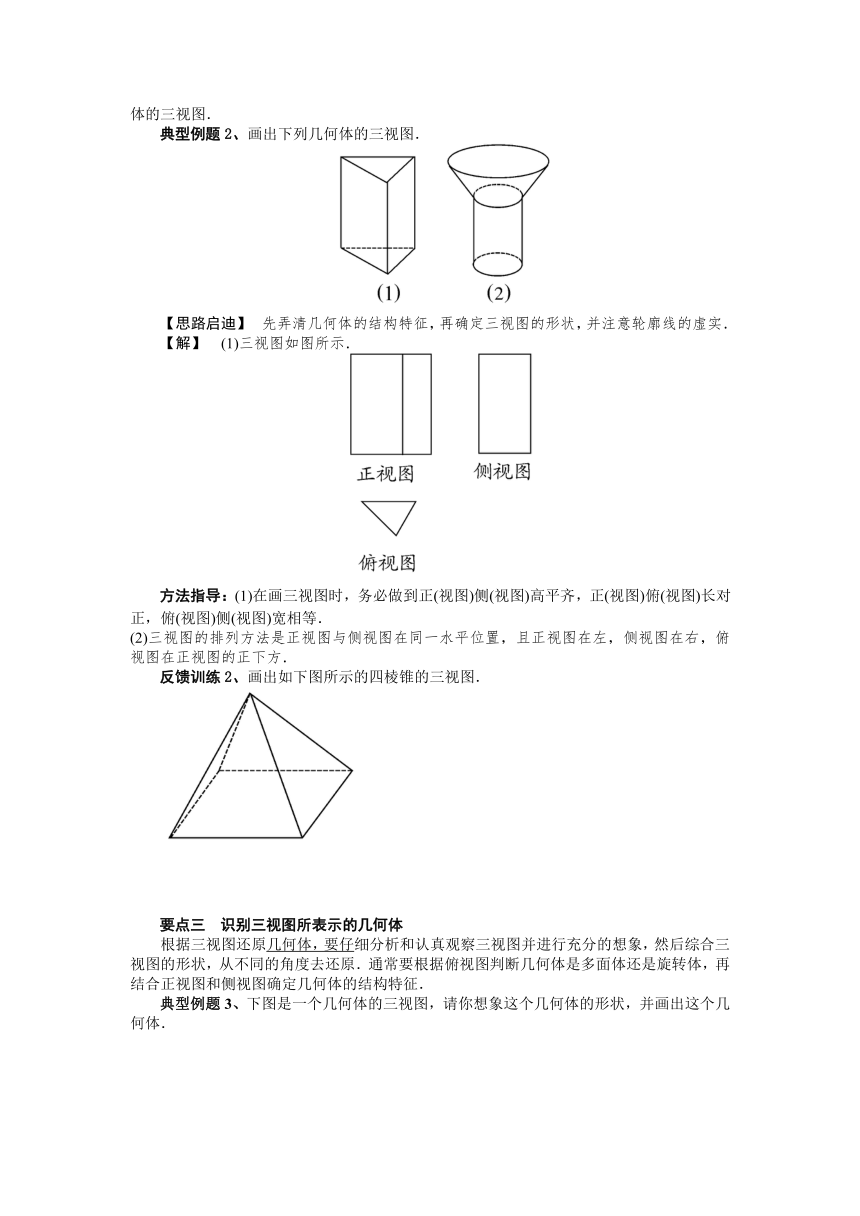
典型例题2、画出下列几何体的三视图.
【思路启迪】 先弄清几何体的结构特征,再确定三视图的形状,并注意轮廓线的虚实.
【解】 (1)三视图如图所示.
方法指导:(1)在画三视图时,务必做到正(视图)侧(视图)高平齐,正(视图)俯(视图)长对正,俯(视图)侧(视图)宽相等.
(2)三视图的排列方法是正视图与侧视图在同一水平位置,且正视图在左,侧视图在右,俯视图在正视图的正下方.
反馈训练2、画出如下图所示的四棱锥的三视图.
要点三
识别三视图所表示的几何体
根据三视图还原几何体,要仔
( http: / / www.21cnjy.com )细分析和认真观察三视图并进行充分的想象,然后综合三视图的形状,从不同的角度去还原.通常要根据俯视图判断几何体是多面体还是旋转体,再结合正视图和侧视图确定几何体的结构特征.
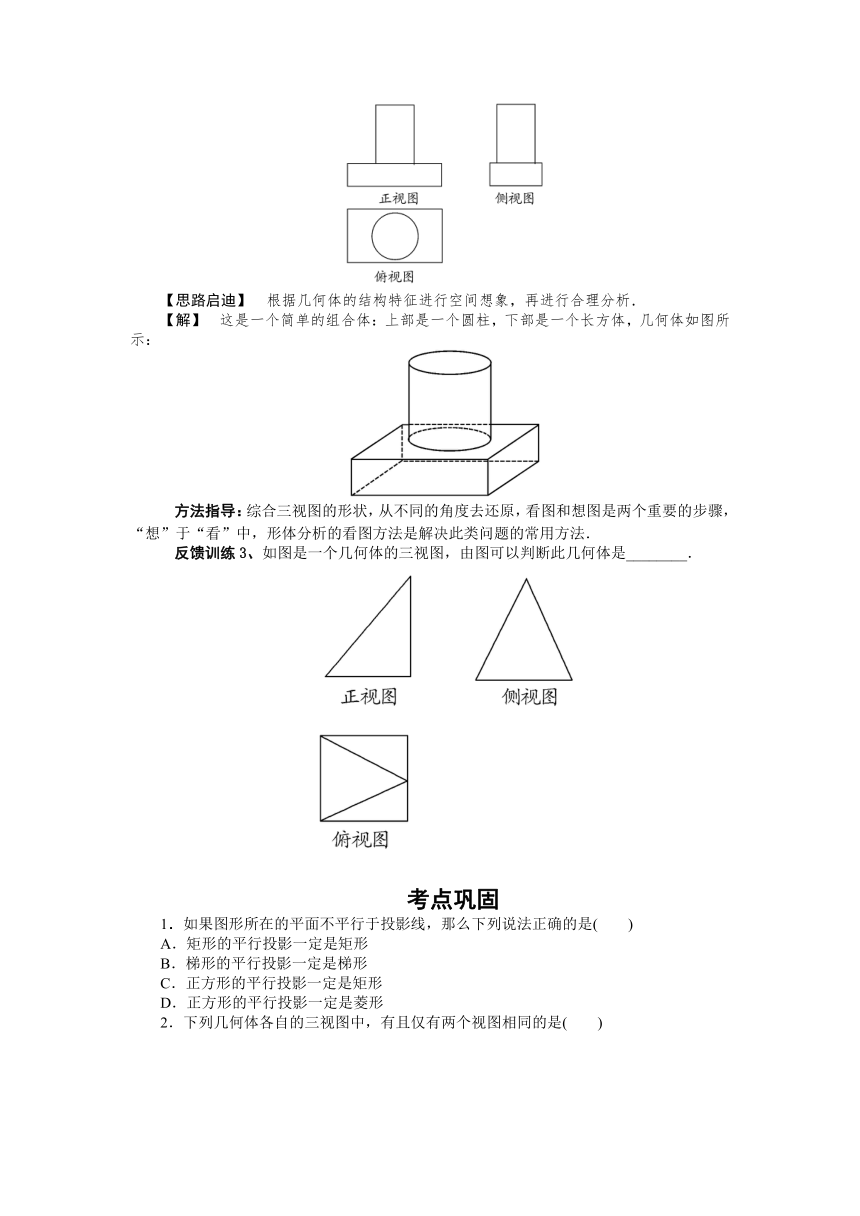
典型例题3、下图是一个几何体的三视图,请你想象这个几何体的形状,并画出这个几何体.
【思路启迪】 根据几何体的结构特征进行空间想象,再进行合理分析.
【解】 这是一个简单的组合体:上部是一个圆柱,下部是一个长方体,几何体如图所示:
方法指导:综合三视图的形状,从不同的角度去还原,看图和想图是两个重要的步骤,“想”于“看”中,形体分析的看图方法是解决此类问题的常用方法.
反馈训练3、如图是一个几何体的三视图,由图可以判断此几何体是________.
考点巩固
1.如果图形所在的平面不平行于投影线,那么下列说法正确的是( )
A.矩形的平行投影一定是矩形
B.梯形的平行投影一定是梯形
C.正方形的平行投影一定是矩形
D.正方形的平行投影一定是菱形
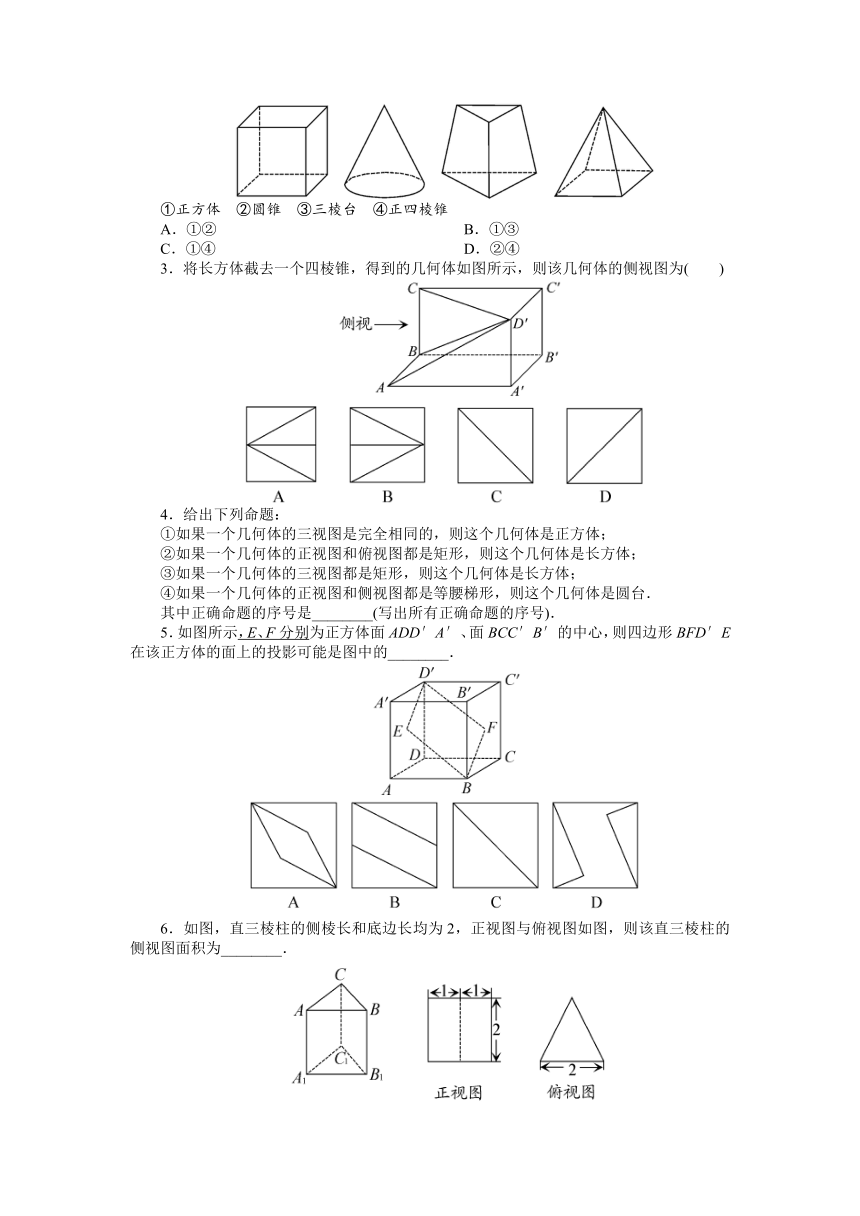
2.下列几何体各自的三视图中,有且仅有两个视图相同的是( )
①正方体 ②圆锥 ③三棱台 ④正四棱锥
A.①②
B.①③
C.①④
D.②④
3.将长方体截去一个四棱锥,得到的几何体如图所示,则该几何体的侧视图为( )
4.给出下列命题:
①如果一个几何体的三视图是完全相同的,则这个几何体是正方体;
②如果一个几何体的正视图和俯视图都是矩形,则这个几何体是长方体;
③如果一个几何体的三视图都是矩形,则这个几何体是长方体;
④如果一个几何体的正视图和侧视图都是等腰梯形,则这个几何体是圆台.
其中正确命题的序号是________(写出所有正确命题的序号).
5.如图所示,E、F分别
( http: / / www.21cnjy.com )为正方体面ADD′A′、面BCC′B′的中心,则四边形BFD′E在该正方体的面上的投影可能是图中的________.
6.如图,直三棱柱的侧棱长和底边长均为2,正视图与俯视图如图,则该直三棱柱的侧视图面积为________.
7.如图所示的几何体是由一个长方体木块锯成的.
(1)判断该几何体是否为棱柱;
(2)画出它的三视图.
8.如图是用小正方体搭的一个几何体的正视图与俯视图,它最少需要多少个小正方体?最多需要多少个小正方体?
考点归纳-答案
1、解析:从平行投影的性质进行分析,平行投影只保持平行性,其他的如垂直、夹角等则不一定保持.
答案:B
2、解析:①正方体,三视图均相同;②圆锥,正视图和侧视图相同;③三棱台,三视图各不相同;④正四棱锥,正视图和侧视图相同.
答案:D
3、解析:根据正投影的性质,并结合侧视
( http: / / www.21cnjy.com )图要求及如图所示,AB的正投影为A′B′,BC的正投影为B′C′,BD′的正投影为B′D′,综上可知侧视图为选项D.
答案:D
4、解析:①中三视图完全相同的还可以是
( http: / / www.21cnjy.com )球;②中如果将一个圆柱横放,则其正视图和俯视图都是矩形;④中正视图和侧视图都是等腰梯形的几何体还可以是棱台.故正确的是③.
答案:③
5、解析:四边形BFD′E在正方体
( http: / / www.21cnjy.com )ABCD-A′B′C′D′的面ADD′A′和BCC′B′上的射影是C;在面DCC′D′上的射影是B,同理,在面ABB′A′、面ABCD、面A′B′C′D′上的射影也全是B.
答案:BC
6、解析:该直三棱柱的侧视图是长为2,宽为的矩形,其面积为2.
答案:2
7、解:(1)是棱柱.因为该几何体的前、后两个面互相平行,其余各面都是矩形,而且相邻矩形的公共边都互相平行.
(2)该几何体的三视图如图所示.
8、解:最少需要9个小正方体;最多需要15个小正方体.
1.2.3空间几何体的直观图
【考纲要求】
[学习目标]
1.了解“斜二测画法”的概念并掌握斜二测画法的步骤.
2.会用斜二测画法画出一些简单平面图形和立体图形的直观图.
3.通过观察三视图和直观图,了解空间图形的不同表示形式及不同形式间的联系.
[目标解读]
1.斜二测画法的概念是重点;
2.应用斜二测画法画平面图形和立体图形的直观图是难点.
【自主学习】
1.直观图
空间几何体的直观图通常是在
投影下画出的空间图形.
2.用斜二测画法画水平放置的平面图形的直观图的步骤
(1)画轴:在已知图形中取互相垂直的x轴
( http: / / www.21cnjy.com )和y轴,两轴相交于点O.画直观图时,把它们分别画成对应的x′轴与y′轴,其交点为O′,且使∠x′O′y′=
(或
),它们确定的平面表示
.
3.立体图形直观图的画法
画立体图形的直观图,在画轴时,要多画一条与平面
x′O′y′垂直的轴O′z′,使∠x′O′z′=
,且平行于O′z′的线段长度
.
【考点突破】
要点一
水平放置的平面图形的直观图的画法
1.用斜二测画法画直观图要掌握:水平
( http: / / www.21cnjy.com )长不变,垂线长减半,直角化成45°,遮挡线条改虚线,竖线长也不变,也就是把握住一斜——已知图形中垂直于x轴的线段,在直观图中与x轴成45°或135°;二测——两种度量形式,即在直观图中,平行于x轴的线段长度不变,平行于y轴的线段变为原长度的一半.
2.画水平放置的平面图形的直观图,关键是确定多边形顶点的位置,借助于平面直角坐标系确定顶点后,只需把这些顶点顺次连接即可.
典型例题1、如图是由正方形ABCE和正三角形CDE所构成的平面图形,请画出其水平放置的直观图.
【解】 (1)以AB所在直线为x轴,AB的中垂线为y轴建立直角坐标系(如图(1)),再建立坐标系
x′O′y′,使两轴的夹角为45°(如图(2));
(2)以O′为中点,在x′轴上截取A′
( http: / / www.21cnjy.com )B′=AB;分别过A′,B′作y′轴的平行线,截取A′E′=AE,B′C′=BC.在y′轴上截取O′D′=OD.
(3)连接E′D′,E′C′,C′D′,得到平面图形A′B′C′D′E′.
(3)擦去辅助线,就得到所求的直观图(如图(3)).
方法指导:利用斜二测画法画直观图时应注意:
(1)在已知图形中x轴,y轴的选取,应尽可能多的使图形的点落在坐标轴上,有的点不满足时应作辅助线,与x轴,y轴垂直的线段是最常用的辅助线.
(2)垂直于x轴,y轴的线段在坐标系x′O′y′下的长度变化切勿混淆.
反馈训练1、用斜二测画法画边长为4
cm的水平放置的正三角形的直观图.
要点二
空间几何体的直观图的画法
几何体的直观图的画法规则,与平
( http: / / www.21cnjy.com )面图形的画法相比,只是多画一个与x轴、y轴都垂直的z轴,并且平行于z轴的线段的平行性和长度都不变.在直观图上,x′O′y′表示水平平面,平面y′O′z′和平面z′O′x′表示直立平面.
画空间图形的直观图的原则:
1.首先在原几何体上建立空间直角坐标系O-xyz,并且把它们画成对应的x′轴与y′轴,两轴交于点O′,且使
∠x′O′y′=45°(或135°),它们确定的平面表示水平面,再作z′轴与x′轴垂直.
2.作空间图形的直观图时平行于x轴的线段画成平行于x′轴的线段并且长度不变.
典型例题2、画正六棱柱(底面是正六边形,侧棱垂直于底面)的直观图.
【思路启迪】 先画底面,即先按照水平放置的平面图形的直观图的画法画正六边形,再画侧棱,最后成图.
【解】 画法:(1)画轴.画x′轴、y′轴、z′轴,使∠x′O′y′=45°(或135°),∠x′O′z′=90°.
(2)画底面.按x′轴,y′轴,画正六边形的直观图ABCDEF.
(3)画侧棱.过A、B、C、D、E、F
( http: / / www.21cnjy.com )各点分别作z′轴的平行线,在这些平行线上分别截取AA′、BB′、CC′、DD′、EE′、FF′都等于侧棱长.
(4)成图.顺次连接A′、B′、C′、D′、E′、F′,并加以整理(去掉辅助线,将被遮挡的部分改为虚线,就得到正六棱柱的直观图).
方法指导:(1)空间几何体直观图的画法规则
( http: / / www.21cnjy.com )与平面图形的画法相比,只是多画一个与x轴和y轴都垂直的z轴,表示竖直方向;平行于z轴或在z轴上的线段,方向与长度都与原来保持一致.
(2)对于一些常见几何体(柱、锥、台、球)的直观图,应该记住它们的大致形状,以便可以较快、较准确地画出来.
第一步:作水平放置的正方形的直观图ABCD,使∠BAD=45°,AB=2cm,AD=1cm.
第二步:过A作z′轴,使∠B
( http: / / www.21cnjy.com )Az′=90°.分别过点B,C,D作z′轴的平行线,在z′轴及这组平行线上分别截取AA′=BB′=CC′=DD′=2cm.
第三步:连接A′B′,B′C′,C′D′,D′A′,得到的图形就是所求正方体的直观图.
反馈训练2、画长、宽、高分别是4cm、3cm、2cm的长方体ABCD-A’B’C’D’的直观图。
要点三
将直观图还原为平面图形
给出直观图来研究原图形,逆向运用斜二测
( http: / / www.21cnjy.com )画法规则,要求我们具有逆向思维的能力.画法关键之处同样是关键点的确定,逆向的规则为“水平长不变,垂直长增倍”,注意平行于y′轴的线段与平行于x′轴的线段为垂直关系.
典型例题3、已知水平放置的平面图形的直观图是边长为1的正三角形ABC,求原图的面积.
【思路启迪】 根据斜二测画法的原则递推画出原三角形.
【解】 如下图①所示,作AD⊥BC于D,延长DB到E,使DE=AD,连接AE,则∠AEC=45°.
画E′C′=EC,E′B′=EB,B′D′=BD.
过E′作E′A′⊥E′C′,使E′A′=2EA,
连接A′C′,A′B′,则△A′B′C′就是原来的图形(如上图②所示).
这里B′C′=BC=1,A′E′=2AE=2AD=2×=,
∴△A′B′C′的面积为S=B′C′·A′E′=×1×=.
方法指导:把直观图还原为平面图形是画直观图的递推过程,解题时要正确运用斜二测画法,特别是对应边的长度应准确无误.
反馈训练3、水平放置的△ABC的斜二测直观图如图所示,已知A′C′=3,B′C′=2,则AB边上的中线的实际长度为________.
考点巩固
1.利用斜二测画法得到:
①三角形的直观图是三角形;②平行四边形的直观图是平行四边形;③正方形的直观图是正方形;④菱形的直观图是菱形
以上结论中正确的是( )
A.①②
B.①
C.③④
D.①②③④
2.如下图所示是△AOB用斜二测画法画出的直观图,则△AOB的面积是( )
A.8 B.16 C.32 D.64
3.已知正三角形ABC的边长为a,那么△ABC的平面直观图△A′B′C′的面积为( )
A.a2
B.a2
C.a2
D.a2
4.如图所示的正方形O′A′B′C′的边长为1
cm,它是水平放置的一个平面图形的直观图,则原图形的周长是________.
5.在水平放置的平面M内有一边长为1的
( http: / / www.21cnjy.com )正方形A′B′C′D′,如图所示,其中对角线A′C′在水平位置,已知该正方形是某个四边形用斜二测画法画出的直观图,则真实图形的面积为________.
6.△ABC水平放置的直观图形如下图所示,O′A=O′B=O′C=2
cm,那么:
(1)△ABC的形状如何?
(2)△ABC的面积是多少?
7.如图是一梯形OABC的直观图,其直观图面积为S,求梯形OABC的面积.
8.如图是一个几何体的三视图,用斜二测画法画出它的直观图.
考点巩固-答案
1、解析:斜二测画法保持平行性和相交性不
( http: / / www.21cnjy.com )变,即平行直线的直观图还是平行直线,相交直线的直观图还是相交直线,故①②正确;但是斜二测画法中平行于y轴的线段,在直观图中长度为原来的一半,则正方形的直观图不是正方形,菱形的直观图不是菱形,所以③④错.
答案:A
2、解析:由图可知△AOB的底边长为4,高为16,所以面积为×4×16=32.
答案:C
3、解析:如图①②所示的实际图形和直观图.
由图②可知,A′B′=AB=a,O′C′=OC=a,
在图②中作C′D′⊥A′B′于D′,
则C′D′=O′C′=a.
∴S△A′B′C′=A′B′·C′D′=×a×a=a2.
答案:D
4、解析:直观图中,O′B′=,原图形中OC=AB==3,OA=BC=1,∴原图形的周长是2×(3+1)=8.
答案:8
5、
解析:因为四边形A′B′C′D′是斜二测画法
( http: / / www.21cnjy.com )的直观图,且A′C′在水平位置,所以在真实图形中,D′A′所在边应该垂直A′C′所在边,B′C′所在边应该垂直A′C′所在边,如图所示.因为四边形水平放置,
A′B′C′D′为正方形,所以在四边
( http: / / www.21cnjy.com )形ABCD中DA⊥AC,又因为DA=2D′A′=2,AC=A′C′=,所以S四边形ABCD=AC·AD=2.
答案:2
6、
解:将直观图还原为原图形如图所示:
(1)△ABC为等腰三角形.
(2)由(1)知,该△ABC为等腰三角形.
∴S△ABC=×4×4=8(cm2).
7、解:设O′C′=h,则原梯形是一个直角梯形且高为2h.
C′B′=CB,O′A′=OA.
过C′作C′D⊥O′A′于D,则C′D=h.
由题意知C′D′(C′B′+O′A′)=S,
即h(C′B′+O′A′)=S.
又原直角梯形面积为
S′=·2h(CB+OA)=h(C′B′+O′A′)==2S.
所以梯形OABC的面积为2S.
8、解:(1)画轴.如图①,画x轴、y轴、z轴,使∠xOy=45°,∠xOz=90°.
(2)画底面,利用斜二测画法画出底面A
( http: / / www.21cnjy.com )BCD,在z轴上截取O′,使OO′等于三视图中相应高度,过O′作Ox的平行线O′x′,Oy的平行线O′y′,利用O′x′与O′y′画出上底面A′B′C′D′.
(3)画正四棱锥顶点.在Oz上截取点P,使PO′等于三视图中相应的高度.
(4)成图.连接PA′、PB′、PC′、PD′、A′A、B′B、C′C、D′D,整理得到三视图表示的几何体的直观图如图②所示.
1.2.1中心投影与平行投影
1.2.2空间几何体的三视图
【考纲要求】
[学习目标]
1.了解中心投影和平行投影.
2.能画出简单空间图形(柱、锥、台、球及其组合体)的三视图.
3.能识别三视图所表示的立体模型.
[目标解读]
1.会画简单空间图形的三视图是重点;
2.识别三视图所表示的立体模型是难点.
【自主学习】
1.投影
(1)投影的定义
由于光的照射,在
物体后面
( http: / / www.21cnjy.com )的屏幕上可以留下这个物体的
,这种现象叫做投影.其中,我们把
叫做投影线,把
的屏幕叫做投影面.
(2)投影的分类
①中心投影:光由
散射形成的投影.
②平行投影:在一束
照射下形成的投影.
当投影线
时,叫做正投影,否则叫做
.
(3)投影的性质
①中心投影的性质:中心投影的
交于一点;当光源距离物体越近,投影形成的影子
.
②平行投影的性质:平行投影的投影线
.
2.三视图
(1)分类
①正视图:光线从几何体的
向
正投影,得到的投影图;
②侧视图:光线从几何体的
向
正投影,得到的投影图;
③俯视图:光线从几何体的
向
正投影,得到的投影图.
(2)三视图的画法规则
①
视图都反映物体的长度——“长对正”;
②
视图都反映物体的高度——“高平齐”;
③
视图都反映物体的宽度——“宽相等”.
特别提醒:画几何体的三视图时,能看见的轮廓线和棱用实线表示,不能看见的轮廓线和棱用虚线表示.
【考点突破】
要点一
平行投影与中心投影
中心投影与平行投影都是空间图形的基本画法,
( http: / / www.21cnjy.com )是投影的两种形式.通过中心投影与平行投影将三维物体转换成二维平面物体,可以通过投影想象实际物体的形状,但还不能完全反映真实情况,只能反映部分形状,只有在特殊情况下反映真实尺寸.
画立体几何图形时一般采用平行投影法,画实际
( http: / / www.21cnjy.com )效果图时采用中心投影法,中心投影的投影线交于一点,点光源离物体越近,投影形成的影子越大;平行投影的投影线是平行的.
典型例题1、在正方体ABCD-A′B′C′D′中,E、F分别是A′A、C′C的中点,则下列判断正确的是________.
①四边形BFD′E在底面ABCD内的投影是正方形
②四边形BFD′E在面A′D′DA内的投影是菱形
③四边形BFD′E在面A′D′DA内的投影与在面ABB′A′内的投影是全等的平行四边形
【思路启迪】 先根据平行投影的定义知投影线垂直于投影面,从而确定四边形BFD′E四点在各投影面的位置.再把各投影点连线成图.
【解析】 ①四边形BFD′E的四个顶点在底面ABCD内的投影分别是点B、C、D、A,故投影是正方形,正确;
②设正方体的边长为2,则A
( http: / / www.21cnjy.com )E=1,取D′D的中点G,则四边形BFD′E在面A′D′DA内的投影是四边形AGD′E,由AE∥D′G,且AE=D′G,∴四边形AGD′E是平行四边形.但AE=1,D′E=,故四边形AGD′E不是菱形.对于③,由②知是两个边长分别相等的平行四边形,从而③正确.
方法指导:画出一个图形在一个投影面上的
( http: / / www.21cnjy.com )投影的关键是确定该图形的关键点(如顶点,端点等),先画出这些关键点的投影,再依次连接即可得此图形在投影面上的投影.
反馈训练1、如图甲所示,在正方体A
( http: / / www.21cnjy.com )BCD-A1B1C1D1中,E、F分别是AA1、C1D1的中点,G是正方形BCC1B1的中心,则四边形AGFE在该正方体的各个面上的投影可能是图乙中的________.
要点二
画空间几何体的三视图
1.三视图是用两两相互垂直的三个平
( http: / / www.21cnjy.com )面(正面、侧面、水平面)作为投影面,把物体放在这个空间内,分别向三个平面进行正投影,然后将水平投影绕水平面和正面的交线向下转90°,将侧面投影绕侧面和正面的交线向右转90°,就得到了三视图,即画出的三视图需要符合长对正、高平齐、宽相等的基本特征.
2.画简单组合体的三视图时,先要分析该组合体
( http: / / www.21cnjy.com )的结构特征,再想象模型,从正前方、左方、正上方三个不同角度各能看到什么形状,再借助简单几何体的三视图,画出简单组合体的三视图.
典型例题2、画出下列几何体的三视图.
【思路启迪】 先弄清几何体的结构特征,再确定三视图的形状,并注意轮廓线的虚实.
【解】 (1)三视图如图所示.
方法指导:(1)在画三视图时,务必做到正(视图)侧(视图)高平齐,正(视图)俯(视图)长对正,俯(视图)侧(视图)宽相等.
(2)三视图的排列方法是正视图与侧视图在同一水平位置,且正视图在左,侧视图在右,俯视图在正视图的正下方.
反馈训练2、画出如下图所示的四棱锥的三视图.
要点三
识别三视图所表示的几何体
根据三视图还原几何体,要仔
( http: / / www.21cnjy.com )细分析和认真观察三视图并进行充分的想象,然后综合三视图的形状,从不同的角度去还原.通常要根据俯视图判断几何体是多面体还是旋转体,再结合正视图和侧视图确定几何体的结构特征.
典型例题3、下图是一个几何体的三视图,请你想象这个几何体的形状,并画出这个几何体.
【思路启迪】 根据几何体的结构特征进行空间想象,再进行合理分析.
【解】 这是一个简单的组合体:上部是一个圆柱,下部是一个长方体,几何体如图所示:
方法指导:综合三视图的形状,从不同的角度去还原,看图和想图是两个重要的步骤,“想”于“看”中,形体分析的看图方法是解决此类问题的常用方法.
反馈训练3、如图是一个几何体的三视图,由图可以判断此几何体是________.
考点巩固
1.如果图形所在的平面不平行于投影线,那么下列说法正确的是( )
A.矩形的平行投影一定是矩形
B.梯形的平行投影一定是梯形
C.正方形的平行投影一定是矩形
D.正方形的平行投影一定是菱形
2.下列几何体各自的三视图中,有且仅有两个视图相同的是( )
①正方体 ②圆锥 ③三棱台 ④正四棱锥
A.①②
B.①③
C.①④
D.②④
3.将长方体截去一个四棱锥,得到的几何体如图所示,则该几何体的侧视图为( )
4.给出下列命题:
①如果一个几何体的三视图是完全相同的,则这个几何体是正方体;
②如果一个几何体的正视图和俯视图都是矩形,则这个几何体是长方体;
③如果一个几何体的三视图都是矩形,则这个几何体是长方体;
④如果一个几何体的正视图和侧视图都是等腰梯形,则这个几何体是圆台.
其中正确命题的序号是________(写出所有正确命题的序号).
5.如图所示,E、F分别
( http: / / www.21cnjy.com )为正方体面ADD′A′、面BCC′B′的中心,则四边形BFD′E在该正方体的面上的投影可能是图中的________.
6.如图,直三棱柱的侧棱长和底边长均为2,正视图与俯视图如图,则该直三棱柱的侧视图面积为________.
7.如图所示的几何体是由一个长方体木块锯成的.
(1)判断该几何体是否为棱柱;
(2)画出它的三视图.
8.如图是用小正方体搭的一个几何体的正视图与俯视图,它最少需要多少个小正方体?最多需要多少个小正方体?
考点归纳-答案
1、解析:从平行投影的性质进行分析,平行投影只保持平行性,其他的如垂直、夹角等则不一定保持.
答案:B
2、解析:①正方体,三视图均相同;②圆锥,正视图和侧视图相同;③三棱台,三视图各不相同;④正四棱锥,正视图和侧视图相同.
答案:D
3、解析:根据正投影的性质,并结合侧视
( http: / / www.21cnjy.com )图要求及如图所示,AB的正投影为A′B′,BC的正投影为B′C′,BD′的正投影为B′D′,综上可知侧视图为选项D.
答案:D
4、解析:①中三视图完全相同的还可以是
( http: / / www.21cnjy.com )球;②中如果将一个圆柱横放,则其正视图和俯视图都是矩形;④中正视图和侧视图都是等腰梯形的几何体还可以是棱台.故正确的是③.
答案:③
5、解析:四边形BFD′E在正方体
( http: / / www.21cnjy.com )ABCD-A′B′C′D′的面ADD′A′和BCC′B′上的射影是C;在面DCC′D′上的射影是B,同理,在面ABB′A′、面ABCD、面A′B′C′D′上的射影也全是B.
答案:BC
6、解析:该直三棱柱的侧视图是长为2,宽为的矩形,其面积为2.
答案:2
7、解:(1)是棱柱.因为该几何体的前、后两个面互相平行,其余各面都是矩形,而且相邻矩形的公共边都互相平行.
(2)该几何体的三视图如图所示.
8、解:最少需要9个小正方体;最多需要15个小正方体.
1.2.3空间几何体的直观图
【考纲要求】
[学习目标]
1.了解“斜二测画法”的概念并掌握斜二测画法的步骤.
2.会用斜二测画法画出一些简单平面图形和立体图形的直观图.
3.通过观察三视图和直观图,了解空间图形的不同表示形式及不同形式间的联系.
[目标解读]
1.斜二测画法的概念是重点;
2.应用斜二测画法画平面图形和立体图形的直观图是难点.
【自主学习】
1.直观图
空间几何体的直观图通常是在
投影下画出的空间图形.
2.用斜二测画法画水平放置的平面图形的直观图的步骤
(1)画轴:在已知图形中取互相垂直的x轴
( http: / / www.21cnjy.com )和y轴,两轴相交于点O.画直观图时,把它们分别画成对应的x′轴与y′轴,其交点为O′,且使∠x′O′y′=
(或
),它们确定的平面表示
.
3.立体图形直观图的画法
画立体图形的直观图,在画轴时,要多画一条与平面
x′O′y′垂直的轴O′z′,使∠x′O′z′=
,且平行于O′z′的线段长度
.
【考点突破】
要点一
水平放置的平面图形的直观图的画法
1.用斜二测画法画直观图要掌握:水平
( http: / / www.21cnjy.com )长不变,垂线长减半,直角化成45°,遮挡线条改虚线,竖线长也不变,也就是把握住一斜——已知图形中垂直于x轴的线段,在直观图中与x轴成45°或135°;二测——两种度量形式,即在直观图中,平行于x轴的线段长度不变,平行于y轴的线段变为原长度的一半.
2.画水平放置的平面图形的直观图,关键是确定多边形顶点的位置,借助于平面直角坐标系确定顶点后,只需把这些顶点顺次连接即可.
典型例题1、如图是由正方形ABCE和正三角形CDE所构成的平面图形,请画出其水平放置的直观图.
【解】 (1)以AB所在直线为x轴,AB的中垂线为y轴建立直角坐标系(如图(1)),再建立坐标系
x′O′y′,使两轴的夹角为45°(如图(2));
(2)以O′为中点,在x′轴上截取A′
( http: / / www.21cnjy.com )B′=AB;分别过A′,B′作y′轴的平行线,截取A′E′=AE,B′C′=BC.在y′轴上截取O′D′=OD.
(3)连接E′D′,E′C′,C′D′,得到平面图形A′B′C′D′E′.
(3)擦去辅助线,就得到所求的直观图(如图(3)).
方法指导:利用斜二测画法画直观图时应注意:
(1)在已知图形中x轴,y轴的选取,应尽可能多的使图形的点落在坐标轴上,有的点不满足时应作辅助线,与x轴,y轴垂直的线段是最常用的辅助线.
(2)垂直于x轴,y轴的线段在坐标系x′O′y′下的长度变化切勿混淆.
反馈训练1、用斜二测画法画边长为4
cm的水平放置的正三角形的直观图.
要点二
空间几何体的直观图的画法
几何体的直观图的画法规则,与平
( http: / / www.21cnjy.com )面图形的画法相比,只是多画一个与x轴、y轴都垂直的z轴,并且平行于z轴的线段的平行性和长度都不变.在直观图上,x′O′y′表示水平平面,平面y′O′z′和平面z′O′x′表示直立平面.
画空间图形的直观图的原则:
1.首先在原几何体上建立空间直角坐标系O-xyz,并且把它们画成对应的x′轴与y′轴,两轴交于点O′,且使
∠x′O′y′=45°(或135°),它们确定的平面表示水平面,再作z′轴与x′轴垂直.
2.作空间图形的直观图时平行于x轴的线段画成平行于x′轴的线段并且长度不变.
典型例题2、画正六棱柱(底面是正六边形,侧棱垂直于底面)的直观图.
【思路启迪】 先画底面,即先按照水平放置的平面图形的直观图的画法画正六边形,再画侧棱,最后成图.
【解】 画法:(1)画轴.画x′轴、y′轴、z′轴,使∠x′O′y′=45°(或135°),∠x′O′z′=90°.
(2)画底面.按x′轴,y′轴,画正六边形的直观图ABCDEF.
(3)画侧棱.过A、B、C、D、E、F
( http: / / www.21cnjy.com )各点分别作z′轴的平行线,在这些平行线上分别截取AA′、BB′、CC′、DD′、EE′、FF′都等于侧棱长.
(4)成图.顺次连接A′、B′、C′、D′、E′、F′,并加以整理(去掉辅助线,将被遮挡的部分改为虚线,就得到正六棱柱的直观图).
方法指导:(1)空间几何体直观图的画法规则
( http: / / www.21cnjy.com )与平面图形的画法相比,只是多画一个与x轴和y轴都垂直的z轴,表示竖直方向;平行于z轴或在z轴上的线段,方向与长度都与原来保持一致.
(2)对于一些常见几何体(柱、锥、台、球)的直观图,应该记住它们的大致形状,以便可以较快、较准确地画出来.
第一步:作水平放置的正方形的直观图ABCD,使∠BAD=45°,AB=2cm,AD=1cm.
第二步:过A作z′轴,使∠B
( http: / / www.21cnjy.com )Az′=90°.分别过点B,C,D作z′轴的平行线,在z′轴及这组平行线上分别截取AA′=BB′=CC′=DD′=2cm.
第三步:连接A′B′,B′C′,C′D′,D′A′,得到的图形就是所求正方体的直观图.
反馈训练2、画长、宽、高分别是4cm、3cm、2cm的长方体ABCD-A’B’C’D’的直观图。
要点三
将直观图还原为平面图形
给出直观图来研究原图形,逆向运用斜二测
( http: / / www.21cnjy.com )画法规则,要求我们具有逆向思维的能力.画法关键之处同样是关键点的确定,逆向的规则为“水平长不变,垂直长增倍”,注意平行于y′轴的线段与平行于x′轴的线段为垂直关系.
典型例题3、已知水平放置的平面图形的直观图是边长为1的正三角形ABC,求原图的面积.
【思路启迪】 根据斜二测画法的原则递推画出原三角形.
【解】 如下图①所示,作AD⊥BC于D,延长DB到E,使DE=AD,连接AE,则∠AEC=45°.
画E′C′=EC,E′B′=EB,B′D′=BD.
过E′作E′A′⊥E′C′,使E′A′=2EA,
连接A′C′,A′B′,则△A′B′C′就是原来的图形(如上图②所示).
这里B′C′=BC=1,A′E′=2AE=2AD=2×=,
∴△A′B′C′的面积为S=B′C′·A′E′=×1×=.
方法指导:把直观图还原为平面图形是画直观图的递推过程,解题时要正确运用斜二测画法,特别是对应边的长度应准确无误.
反馈训练3、水平放置的△ABC的斜二测直观图如图所示,已知A′C′=3,B′C′=2,则AB边上的中线的实际长度为________.
考点巩固
1.利用斜二测画法得到:
①三角形的直观图是三角形;②平行四边形的直观图是平行四边形;③正方形的直观图是正方形;④菱形的直观图是菱形
以上结论中正确的是( )
A.①②
B.①
C.③④
D.①②③④
2.如下图所示是△AOB用斜二测画法画出的直观图,则△AOB的面积是( )
A.8 B.16 C.32 D.64
3.已知正三角形ABC的边长为a,那么△ABC的平面直观图△A′B′C′的面积为( )
A.a2
B.a2
C.a2
D.a2
4.如图所示的正方形O′A′B′C′的边长为1
cm,它是水平放置的一个平面图形的直观图,则原图形的周长是________.
5.在水平放置的平面M内有一边长为1的
( http: / / www.21cnjy.com )正方形A′B′C′D′,如图所示,其中对角线A′C′在水平位置,已知该正方形是某个四边形用斜二测画法画出的直观图,则真实图形的面积为________.
6.△ABC水平放置的直观图形如下图所示,O′A=O′B=O′C=2
cm,那么:
(1)△ABC的形状如何?
(2)△ABC的面积是多少?
7.如图是一梯形OABC的直观图,其直观图面积为S,求梯形OABC的面积.
8.如图是一个几何体的三视图,用斜二测画法画出它的直观图.
考点巩固-答案
1、解析:斜二测画法保持平行性和相交性不
( http: / / www.21cnjy.com )变,即平行直线的直观图还是平行直线,相交直线的直观图还是相交直线,故①②正确;但是斜二测画法中平行于y轴的线段,在直观图中长度为原来的一半,则正方形的直观图不是正方形,菱形的直观图不是菱形,所以③④错.
答案:A
2、解析:由图可知△AOB的底边长为4,高为16,所以面积为×4×16=32.
答案:C
3、解析:如图①②所示的实际图形和直观图.
由图②可知,A′B′=AB=a,O′C′=OC=a,
在图②中作C′D′⊥A′B′于D′,
则C′D′=O′C′=a.
∴S△A′B′C′=A′B′·C′D′=×a×a=a2.
答案:D
4、解析:直观图中,O′B′=,原图形中OC=AB==3,OA=BC=1,∴原图形的周长是2×(3+1)=8.
答案:8
5、
解析:因为四边形A′B′C′D′是斜二测画法
( http: / / www.21cnjy.com )的直观图,且A′C′在水平位置,所以在真实图形中,D′A′所在边应该垂直A′C′所在边,B′C′所在边应该垂直A′C′所在边,如图所示.因为四边形水平放置,
A′B′C′D′为正方形,所以在四边
( http: / / www.21cnjy.com )形ABCD中DA⊥AC,又因为DA=2D′A′=2,AC=A′C′=,所以S四边形ABCD=AC·AD=2.
答案:2
6、
解:将直观图还原为原图形如图所示:
(1)△ABC为等腰三角形.
(2)由(1)知,该△ABC为等腰三角形.
∴S△ABC=×4×4=8(cm2).
7、解:设O′C′=h,则原梯形是一个直角梯形且高为2h.
C′B′=CB,O′A′=OA.
过C′作C′D⊥O′A′于D,则C′D=h.
由题意知C′D′(C′B′+O′A′)=S,
即h(C′B′+O′A′)=S.
又原直角梯形面积为
S′=·2h(CB+OA)=h(C′B′+O′A′)==2S.
所以梯形OABC的面积为2S.
8、解:(1)画轴.如图①,画x轴、y轴、z轴,使∠xOy=45°,∠xOz=90°.
(2)画底面,利用斜二测画法画出底面A
( http: / / www.21cnjy.com )BCD,在z轴上截取O′,使OO′等于三视图中相应高度,过O′作Ox的平行线O′x′,Oy的平行线O′y′,利用O′x′与O′y′画出上底面A′B′C′D′.
(3)画正四棱锥顶点.在Oz上截取点P,使PO′等于三视图中相应的高度.
(4)成图.连接PA′、PB′、PC′、PD′、A′A、B′B、C′C、D′D,整理得到三视图表示的几何体的直观图如图②所示.
