5.1 变量与函数 同步练习(含答案)
文档属性
| 名称 | 5.1 变量与函数 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 490.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-27 05:34:23 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
5.1 变量与函数
一、单选题
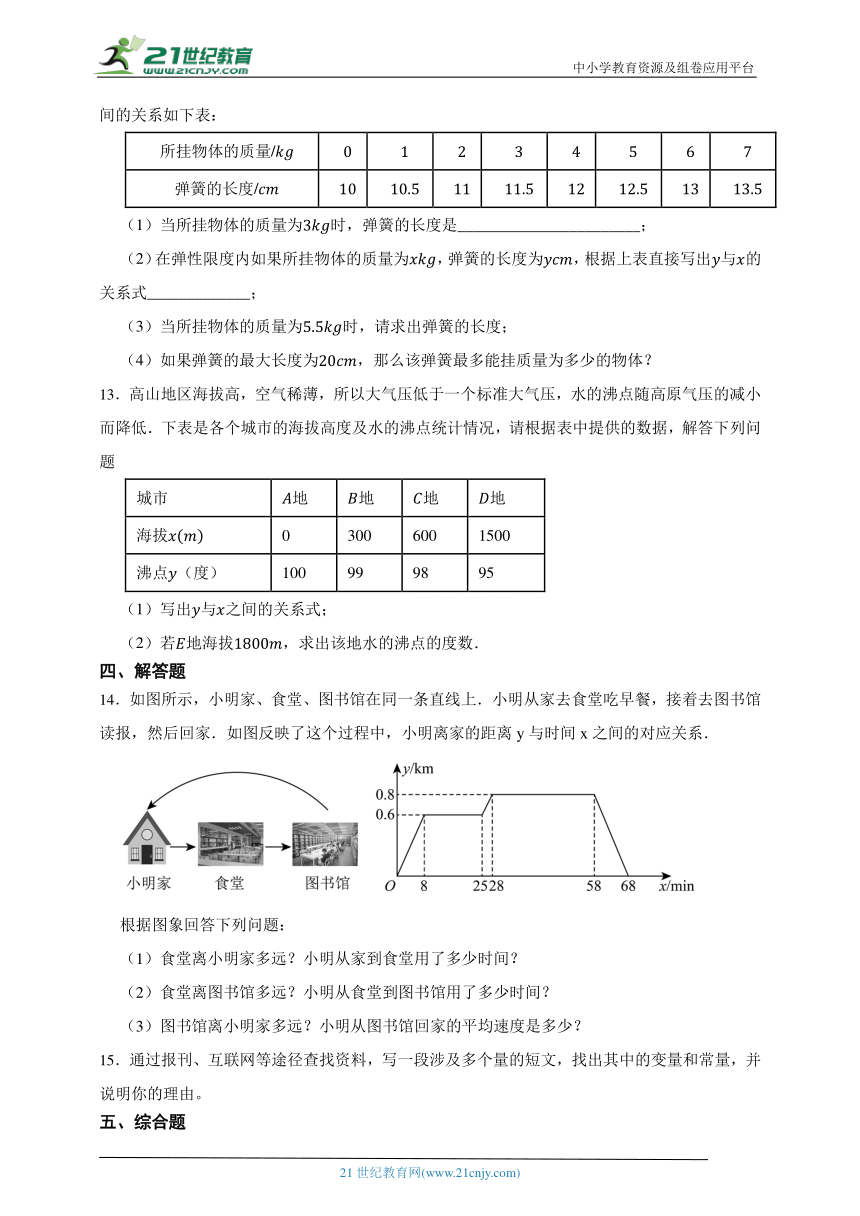
1.下列各曲线表示的与之间的关系中,不是的函数的是( )
A. B.
C. D.
2.已知;;;以上各式中,是的函数的有( )
A.1个 B.2个 C.3个 D.4个
3.水池中原有升水,现每分钟向池内注升,则水池内水量(升)与注水时间(分)之间关系的图象大致为( )
A. B.
C. D.
4.下列图象中,不能表示y是x的函数的是( )
A. B.
C. D.
5.点燃一根蜡烛后,蜡烛的高度(厘米)与燃烧时间(分)之间的关系如表:
(分)
(厘米)
这根蜡烛最多能燃烧的时间为( )
A.分 B.分 C.分 D.分
二、填空题
6.在高处让一物体由静止开始落下,它下落的高度(米)与下落的时间(秒)之间的关系可用来表示,则当下落的时间为4秒时,下落的高度是 米.
7.点燃一根蜡烛后,蜡烛的高度h(厘米)与燃烧时间t(分)之间的关系如下表:
t/分 0 2 4 6 8 10
h/厘米 30 29 28 27 26 25
写出蜡烛的高度h(厘米)与燃烧时间t(分)之间的关系式 .
8.某水果店卖出的苹果数量(千克)与售价(元)之间的关系如下表:
苹果数量x(千克) 0.5 1 1.5 2 2.5 3 3.5 …
售价y(元) 2.5 5 7.5 10 12.5 15 17.5 …
上表反映了两个变量之间的关系,则与的关系式为
9.今年将在法国巴黎举行第33届夏季奥运会.一般情况下夏季奥运会每隔四年举行一次,设第x届夏季奥运会的年份为y,则y与之间的函数关系式为(x、y均为正整数).
10.按如图所示的方式摆放餐桌和椅子,照这样的方式继续摆放,如果摆放的餐桌为张,摆放的椅子为把,则与之间的关系式为 .
11.在函数y= +(x﹣1)0中,自变量x的取值范围是 .
三、计算题
12.探索计算:弹簧挂上物体后会伸长.已知一弹簧的长度()与所挂物体的质量()之间的关系如下表:
所挂物体的质量/
弹簧的长度/
(1)当所挂物体的质量为时,弹簧的长度是_______________________;
(2)在弹性限度内如果所挂物体的质量为,弹簧的长度为,根据上表直接写出与的关系式_____________;
(3)当所挂物体的质量为时,请求出弹簧的长度;
(4)如果弹簧的最大长度为,那么该弹簧最多能挂质量为多少的物体?
13.高山地区海拔高,空气稀薄,所以大气压低于一个标准大气压,水的沸点随高原气压的减小而降低.下表是各个城市的海拔高度及水的沸点统计情况,请根据表中提供的数据,解答下列问题
城市 地 地 地 地
海拔 0 300 600 1500
沸点(度) 100 99 98 95
(1)写出与之间的关系式;
(2)若地海拔,求出该地水的沸点的度数.
四、解答题
14.如图所示,小明家、食堂、图书馆在同一条直线上.小明从家去食堂吃早餐,接着去图书馆读报,然后回家.如图反映了这个过程中,小明离家的距离y与时间x之间的对应关系.
根据图象回答下列问题:
(1)食堂离小明家多远?小明从家到食堂用了多少时间?
(2)食堂离图书馆多远?小明从食堂到图书馆用了多少时间?
(3)图书馆离小明家多远?小明从图书馆回家的平均速度是多少?
15.通过报刊、互联网等途径查找资料,写一段涉及多个量的短文,找出其中的变量和常量,并说明你的理由。
五、综合题
16.随着科技的飞速发展,人工智能()已成为当今社会的热点话题,自动驾驶汽车是一种通过电脑系统实现无人驾驶的智能汽车.某公司为了解自主研发出的一款智能汽车.根据路况调节车速的功能进行了测试.如图表示一辆汽车从出发到最后停止汽车的速度随时间变化而变化的情况.请根据图象回答下列问题:
(1)汽车从出发到最后停止共经过的时间为______分钟;
(2)汽车的最高时速是多少?
(3)汽车在哪段时间保持匀速行驶?时速是多少?
(4)汽车在哪些时间段速度在增加,哪些时间段速度在减小?
17.随着科学技术的不断发展,电动汽车成为人们日常出行的重要交通工具,电动汽车的电池容量与续航里程成为人们最为关心的问题.现对某型号电动汽车充满电后进行测试,其电池剩余电量(度)与行驶里程(千米)之间的关系如下表所示:
行驶里程(千米) 0 10 20 40 …
剩余电量(度) 80 78 76 72 …
(1)表中自变量是________,因变量是__________.
(2)该型号电动汽车的电池容量为______度;
(3)请根据表中直接写出该电动汽车剩余电量(度)与行驶里程(千米)之间的关系式;
(4)求剩余电量为时电动汽车的行驶里程.
18.快车与慢车分別从甲乙两地同时相向出发,匀速而行,快车到达乙地后停留1h,然后按原路原速返回,快车比慢车晚1h到达甲地,快慢两车距各自出发地的路程y(km)与所用的时x(h)的关系如图所示.
(1)甲乙两地之间的路程 km;快车的速度为 km/h;慢车的速度为 km/h;
(2)出发 小时后,快慢两车相遇;
(3)求快慢两车出发几小时后第一次相距150km?
六、实践探究题
19.背景资料:“低碳生活”是指人们生活中尽量减少所耗能量,从而降低碳(特别是二氧化碳)的排放量的一种生活方式,低碳生活的理念也已逐步被人们所接受,相关资料统计了排碳计算公式,如下:
排碳计算公式 家居用电的二氧化碳排放量()=耗电量 开私家车的二氧化碳排放量()=耗油量 家用天然气二氧化碳排放量()=天然气使用量 家用自来水二氧化碳排放量()=自来水使用量
(1)若表示耗油量,开私家车的二氧化碳排放量为,则开私家车的二氧化碳排放量与耗油量的关系式为______.
(2)在上述关系中,耗油量每增加,二氧化碳排放量就增加______;当耗油量从增加到时,二氧化碳排放量就从______增加到______.
(3)小明家本月家居用电约,天然气,自来水,开私家车耗油,请你计算一下小明家这几项二氧化碳排放量的总和.
答案解析部分
1.【答案】D
【知识点】函数的图象
2.【答案】B
【知识点】函数的概念
3.【答案】B
【知识点】函数的图象
4.【答案】A
【知识点】函数的概念
5.【答案】A
【知识点】函数自变量的取值范围;用关系式表示变量间的关系
6.【答案】80
【知识点】函数值
7.【答案】
【知识点】用关系式表示变量间的关系
8.【答案】
【知识点】用表格表示变量间的关系;用关系式表示变量间的关系
9.【答案】
【知识点】函数解析式
10.【答案】
【知识点】函数解析式
11.【答案】x≥-2且x≠1
【知识点】函数自变量的取值范围
12.【答案】(1)
(2)
(3)
(4)
【知识点】用表格表示变量间的关系;用关系式表示变量间的关系
13.【答案】(1);
(2)94度
【知识点】函数解析式;函数自变量的取值范围
14.【答案】(1);
(2);
(3);
【知识点】通过函数图象获取信息
15.【答案】解:一次乌龟与兔子举行500m赛跑,比赛开始不久,兔子就遥遥领先,当兔子以50m/min的速度跑了4min时,往回一看,乌龟远远地落在后面呢!兔子心想:“我就是睡一觉,你乌龟也追不上我,我为何不在此美美地睡上一觉呢 ”可是,当骄傲的兔子正做着胜利者的美梦时,勤勉的乌龟却从它身边悄悄爬过,并以10m/min的速度匀速爬向终点.46min后,兔子梦醒了,而此时乌龟刚好到达终点.兔子悔之晚矣!等它再以60m/min的速度跑向终点时,它比乌龟晚了5min.
500m、乌龟的速度10m/min等在整个变化过程中是常量,兔子的速度是变量
【知识点】常量、变量
16.【答案】(1);
(2)汽车的最高时速是;
(3)汽车在至分钟保持匀速行驶,汽车的时速是;
(4)汽车在至分钟,在至分钟速度在增加,汽车在至分钟,在至分钟速度在减小.
【知识点】通过函数图象获取信息
17.【答案】(1)行驶里程(千米);剩余电量(度)
(2)80
(3)
(4)300千米
【知识点】函数自变量的取值范围;用表格表示变量间的关系;用关系式表示变量间的关系
18.【答案】(1)560;140;70
(2)
(3)解:快慢两车出发b小时后第一次相距150km,
140b+70b=560﹣150,
解得,b= ,
即快慢两车出发 小时后第一次相距150km
【知识点】通过函数图象获取信息
19.【答案】(1);
(2)2.7,8.1,21.6;
(3).
【知识点】函数解析式;函数自变量的取值范围;有理数混合运算的实际应用
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
5.1 变量与函数
一、单选题
1.下列各曲线表示的与之间的关系中,不是的函数的是( )
A. B.
C. D.
2.已知;;;以上各式中,是的函数的有( )
A.1个 B.2个 C.3个 D.4个
3.水池中原有升水,现每分钟向池内注升,则水池内水量(升)与注水时间(分)之间关系的图象大致为( )
A. B.
C. D.
4.下列图象中,不能表示y是x的函数的是( )
A. B.
C. D.
5.点燃一根蜡烛后,蜡烛的高度(厘米)与燃烧时间(分)之间的关系如表:
(分)
(厘米)
这根蜡烛最多能燃烧的时间为( )
A.分 B.分 C.分 D.分
二、填空题
6.在高处让一物体由静止开始落下,它下落的高度(米)与下落的时间(秒)之间的关系可用来表示,则当下落的时间为4秒时,下落的高度是 米.
7.点燃一根蜡烛后,蜡烛的高度h(厘米)与燃烧时间t(分)之间的关系如下表:
t/分 0 2 4 6 8 10
h/厘米 30 29 28 27 26 25
写出蜡烛的高度h(厘米)与燃烧时间t(分)之间的关系式 .
8.某水果店卖出的苹果数量(千克)与售价(元)之间的关系如下表:
苹果数量x(千克) 0.5 1 1.5 2 2.5 3 3.5 …
售价y(元) 2.5 5 7.5 10 12.5 15 17.5 …
上表反映了两个变量之间的关系,则与的关系式为
9.今年将在法国巴黎举行第33届夏季奥运会.一般情况下夏季奥运会每隔四年举行一次,设第x届夏季奥运会的年份为y,则y与之间的函数关系式为(x、y均为正整数).
10.按如图所示的方式摆放餐桌和椅子,照这样的方式继续摆放,如果摆放的餐桌为张,摆放的椅子为把,则与之间的关系式为 .
11.在函数y= +(x﹣1)0中,自变量x的取值范围是 .
三、计算题
12.探索计算:弹簧挂上物体后会伸长.已知一弹簧的长度()与所挂物体的质量()之间的关系如下表:
所挂物体的质量/
弹簧的长度/
(1)当所挂物体的质量为时,弹簧的长度是_______________________;
(2)在弹性限度内如果所挂物体的质量为,弹簧的长度为,根据上表直接写出与的关系式_____________;
(3)当所挂物体的质量为时,请求出弹簧的长度;
(4)如果弹簧的最大长度为,那么该弹簧最多能挂质量为多少的物体?
13.高山地区海拔高,空气稀薄,所以大气压低于一个标准大气压,水的沸点随高原气压的减小而降低.下表是各个城市的海拔高度及水的沸点统计情况,请根据表中提供的数据,解答下列问题
城市 地 地 地 地
海拔 0 300 600 1500
沸点(度) 100 99 98 95
(1)写出与之间的关系式;
(2)若地海拔,求出该地水的沸点的度数.
四、解答题
14.如图所示,小明家、食堂、图书馆在同一条直线上.小明从家去食堂吃早餐,接着去图书馆读报,然后回家.如图反映了这个过程中,小明离家的距离y与时间x之间的对应关系.
根据图象回答下列问题:
(1)食堂离小明家多远?小明从家到食堂用了多少时间?
(2)食堂离图书馆多远?小明从食堂到图书馆用了多少时间?
(3)图书馆离小明家多远?小明从图书馆回家的平均速度是多少?
15.通过报刊、互联网等途径查找资料,写一段涉及多个量的短文,找出其中的变量和常量,并说明你的理由。
五、综合题
16.随着科技的飞速发展,人工智能()已成为当今社会的热点话题,自动驾驶汽车是一种通过电脑系统实现无人驾驶的智能汽车.某公司为了解自主研发出的一款智能汽车.根据路况调节车速的功能进行了测试.如图表示一辆汽车从出发到最后停止汽车的速度随时间变化而变化的情况.请根据图象回答下列问题:
(1)汽车从出发到最后停止共经过的时间为______分钟;
(2)汽车的最高时速是多少?
(3)汽车在哪段时间保持匀速行驶?时速是多少?
(4)汽车在哪些时间段速度在增加,哪些时间段速度在减小?
17.随着科学技术的不断发展,电动汽车成为人们日常出行的重要交通工具,电动汽车的电池容量与续航里程成为人们最为关心的问题.现对某型号电动汽车充满电后进行测试,其电池剩余电量(度)与行驶里程(千米)之间的关系如下表所示:
行驶里程(千米) 0 10 20 40 …
剩余电量(度) 80 78 76 72 …
(1)表中自变量是________,因变量是__________.
(2)该型号电动汽车的电池容量为______度;
(3)请根据表中直接写出该电动汽车剩余电量(度)与行驶里程(千米)之间的关系式;
(4)求剩余电量为时电动汽车的行驶里程.
18.快车与慢车分別从甲乙两地同时相向出发,匀速而行,快车到达乙地后停留1h,然后按原路原速返回,快车比慢车晚1h到达甲地,快慢两车距各自出发地的路程y(km)与所用的时x(h)的关系如图所示.
(1)甲乙两地之间的路程 km;快车的速度为 km/h;慢车的速度为 km/h;
(2)出发 小时后,快慢两车相遇;
(3)求快慢两车出发几小时后第一次相距150km?
六、实践探究题
19.背景资料:“低碳生活”是指人们生活中尽量减少所耗能量,从而降低碳(特别是二氧化碳)的排放量的一种生活方式,低碳生活的理念也已逐步被人们所接受,相关资料统计了排碳计算公式,如下:
排碳计算公式 家居用电的二氧化碳排放量()=耗电量 开私家车的二氧化碳排放量()=耗油量 家用天然气二氧化碳排放量()=天然气使用量 家用自来水二氧化碳排放量()=自来水使用量
(1)若表示耗油量,开私家车的二氧化碳排放量为,则开私家车的二氧化碳排放量与耗油量的关系式为______.
(2)在上述关系中,耗油量每增加,二氧化碳排放量就增加______;当耗油量从增加到时,二氧化碳排放量就从______增加到______.
(3)小明家本月家居用电约,天然气,自来水,开私家车耗油,请你计算一下小明家这几项二氧化碳排放量的总和.
答案解析部分
1.【答案】D
【知识点】函数的图象
2.【答案】B
【知识点】函数的概念
3.【答案】B
【知识点】函数的图象
4.【答案】A
【知识点】函数的概念
5.【答案】A
【知识点】函数自变量的取值范围;用关系式表示变量间的关系
6.【答案】80
【知识点】函数值
7.【答案】
【知识点】用关系式表示变量间的关系
8.【答案】
【知识点】用表格表示变量间的关系;用关系式表示变量间的关系
9.【答案】
【知识点】函数解析式
10.【答案】
【知识点】函数解析式
11.【答案】x≥-2且x≠1
【知识点】函数自变量的取值范围
12.【答案】(1)
(2)
(3)
(4)
【知识点】用表格表示变量间的关系;用关系式表示变量间的关系
13.【答案】(1);
(2)94度
【知识点】函数解析式;函数自变量的取值范围
14.【答案】(1);
(2);
(3);
【知识点】通过函数图象获取信息
15.【答案】解:一次乌龟与兔子举行500m赛跑,比赛开始不久,兔子就遥遥领先,当兔子以50m/min的速度跑了4min时,往回一看,乌龟远远地落在后面呢!兔子心想:“我就是睡一觉,你乌龟也追不上我,我为何不在此美美地睡上一觉呢 ”可是,当骄傲的兔子正做着胜利者的美梦时,勤勉的乌龟却从它身边悄悄爬过,并以10m/min的速度匀速爬向终点.46min后,兔子梦醒了,而此时乌龟刚好到达终点.兔子悔之晚矣!等它再以60m/min的速度跑向终点时,它比乌龟晚了5min.
500m、乌龟的速度10m/min等在整个变化过程中是常量,兔子的速度是变量
【知识点】常量、变量
16.【答案】(1);
(2)汽车的最高时速是;
(3)汽车在至分钟保持匀速行驶,汽车的时速是;
(4)汽车在至分钟,在至分钟速度在增加,汽车在至分钟,在至分钟速度在减小.
【知识点】通过函数图象获取信息
17.【答案】(1)行驶里程(千米);剩余电量(度)
(2)80
(3)
(4)300千米
【知识点】函数自变量的取值范围;用表格表示变量间的关系;用关系式表示变量间的关系
18.【答案】(1)560;140;70
(2)
(3)解:快慢两车出发b小时后第一次相距150km,
140b+70b=560﹣150,
解得,b= ,
即快慢两车出发 小时后第一次相距150km
【知识点】通过函数图象获取信息
19.【答案】(1);
(2)2.7,8.1,21.6;
(3).
【知识点】函数解析式;函数自变量的取值范围;有理数混合运算的实际应用
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
