5.3 一次函数的图象与性质 同步练习(含答案)
文档属性
| 名称 | 5.3 一次函数的图象与性质 同步练习(含答案) | 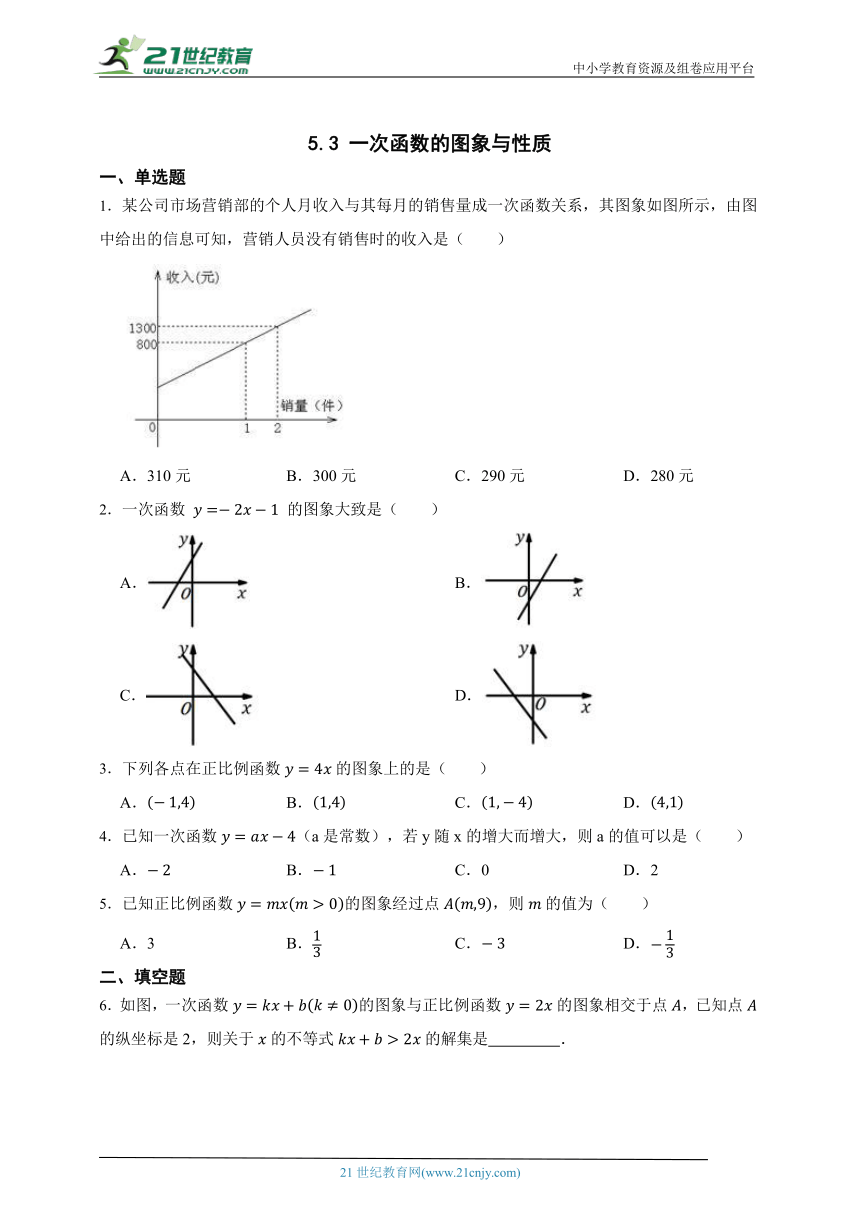 | |
| 格式 | docx | ||
| 文件大小 | 383.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-27 05:33:44 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
5.3 一次函数的图象与性质
一、单选题
1.某公司市场营销部的个人月收入与其每月的销售量成一次函数关系,其图象如图所示,由图中给出的信息可知,营销人员没有销售时的收入是( )
A.310元 B.300元 C.290元 D.280元
2.一次函数 的图象大致是( )
A. B.
C. D.
3.下列各点在正比例函数的图象上的是( )
A. B. C. D.
4.已知一次函数(a是常数),若y随x的增大而增大,则a的值可以是( )
A. B. C.0 D.2
5.已知正比例函数的图象经过点,则的值为( )
A.3 B. C. D.
二、填空题
6.如图,一次函数的图象与正比例函数的图象相交于点,已知点的纵坐标是2,则关于的不等式的解集是 .
7.把直线y=2x﹣1向下平移4个单位,所得直线为 .
8.如图,直线和直线相交于,则关于的不等式解集为 .
9.已知y关于x的一次函数,函数图象经过点,则 ;当时,y的最大值是 .
10.直线与轴的交点坐标为 .
11.从,0,1这三个数中,选取两个不同的数作为一次函数的系数k,b,使一次函数的y值随着x的增大而增大,且图象经过一、三、四象限.则一次函数为 .
三、计算题
12.学习函数的时候我们通过列表、描点和连线的步骤画出函数的图象,进而研究函数的性质.请根据学习“一次函数”时积累的经验和方法研究函数的图象和性质,并解决问题.
(1)若,则函数与x轴交点坐标为(_____,0),与y轴交点坐标为(0,____);
(2)若,根据解析式,写出表格中m,n的值;
x … 0 1 2 3 4 …
y … 11 8 m 2 5 n 11 …
______,_____;
(3)在直角坐标系中画出该函数图象;并写出一条函数的性质:______;
(4)一次函数与该函数图象只有一个交点,则_______.
13.已知一次函数.
(1)当k满足什么条件时,图象经过点?
(2)当k满足什么条件时,y随x的增大而增大?
(3)当k满足什么条件时,图象与y轴的交点为?
四、解答题
14.在数学学习中,及时对知识进行归纳和整理是改善学习的重要方法.善于学习的小明在学习了一次方程(组)、一元一次不等式和一次函数后,对照图形,把相关知识归纳整理如下:
一次函数与方程(组)的关系:
一次函数与不等式的关系:
(1)请你根据以上方框中的内容在下面的数字序号后写出相应的结论:
①______________________; ②______________________,
③______________________; ④______________________.
(2)如果点C的坐标为,那么不等式的解集是___________.
15.在平面直角坐标系中,一次函数的图象由函数的图象平移得到,且经过点.
(1)求该一次函数的表达式;
(2)当时,对于x的每一个值,函数的值大于一次函数的值,直接写出n的取值范围.
五、综合题
16.已知正比例函数y=kx.
(1)若函数图象经过第二、四象限,则k的范围是什么?
(2)点(1,-2)在它的图象上,求它的表达式.
17.已知正比例函数y=kx的图象过点P(3,-3).
(1)写出这个正比例函数的函数解析式;
(2)已知点A(a,2)在这个正比例函数的图象上,求a的值.
18.学生社团作为校园文化的重要载体,是培养学生兴趣爱好,扩大求知领域,陶冶思想情操,展示才华智慧的舞台.某中学社团联合举办了“青春汇聚迎盛会,百团奋进正当时”的主题活动,鼓励学生积极参与社团活动.与此同时,学校计划为参加活动的同学购买一批奖品.经了解,购买2个A种奖品和1个B种奖品需花费64元,购买1个A种奖品和4个B种奖品需花费88元.
(1)求A,B两种奖品的单价;
(2)学校需采购两种奖品共60个,且A种奖品的数量大于B种奖品数量的2倍.设购买A种奖品a个,那么如何购买才能使花费最少?最少花费多少元?
六、实践探究题
19.某数学活动小组结合图象设计如下情景:已知家、书店、学校依次在同一条直线上,书店离家8km,学校离家25km,小明从家出发,匀速骑行0.4h到达书店;在书店停留0.6h后,匀速骑行1h到达学校;在学校学习一段时间,然后回家;回家途中,匀速骑行1h后减速,继续匀速骑行回到家.给出的图象反映了这个过程中小明离家的距离与离开家的时间之间的对应关系.
请根据相关信息解答下列问题:
(1)填表:
离开家的时间/h 0.3 0.8 1.6 3 4.5 5.2
离开家的距离/km
(2)填空:
①书店到学校的距离为 km;
②从学校回家途中减速前的骑行速度为 ;
③当小明离家的距离为2km时,他离开家的时间为 .
答案解析部分
1.【答案】B
【知识点】一次函数的图象
2.【答案】D
【知识点】一次函数图象、性质与系数的关系
3.【答案】B
【知识点】正比例函数的性质
4.【答案】D
【知识点】一次函数的性质
5.【答案】A
【知识点】利用开平方求未知数;正比例函数的性质
6.【答案】
【知识点】一次函数与不等式(组)的关系
7.【答案】y=2x﹣5
【知识点】一次函数图象与几何变换
8.【答案】
【知识点】一次函数的图象;一次函数与不等式(组)的关系;比较一次函数值的大小
9.【答案】2;
【知识点】待定系数法求一次函数解析式;一次函数的性质
10.【答案】(0,-5)
【知识点】一次函数图象与坐标轴交点问题
11.【答案】
【知识点】一次函数图象、性质与系数的关系
12.【答案】(1)1,3;
(2)5,8;
(3)当时,y随x的增大而减小;当时,y随x的增大而增大;
(4).
【知识点】一次函数的概念;一次函数图象与坐标轴交点问题;描点法画函数图象
13.【答案】(1)当时,它的图象经过点;
(2)当时,y随x的增大而减增大
(3)当时,图象与y轴的交点为
【知识点】一次函数图象与坐标轴交点问题;一次函数的性质
14.【答案】(1),,,;(2).
【知识点】一次函数与不等式(组)的关系
15.【答案】(1)
(2)
【知识点】待定系数法求一次函数解析式;一次函数与不等式(组)的关系
16.【答案】(1)解:∵函数图象经过第二、四象限,
∴k<0
(2)解:当x=1,y=-2时,则k=-2,
即:y=-2x
【知识点】正比例函数的图象和性质;待定系数法求一次函数解析式
17.【答案】(1)解:代入求值:-3=3k
K=-1
所以解析式是y=-x
(2)解:点 A(a,2)在图像上.
所以,a=-2
【知识点】正比例函数的图象和性质;待定系数法求一次函数解析式
18.【答案】(1)A种奖品的单价为24元,B种奖品的单价为16元
(2)购买A种奖品41个、B种奖品19个时花费最少,最少为1288元
【知识点】二元一次方程组的其他应用;一元一次不等式的应用;一次函数的性质
19.【答案】(1)解:设小明离家的距离为
由图像可知:当,设,将代入得,,即
当,
当,,将代入得
,解得,
当,
当,,将代入得
,解得,
当,,将代入得
,解得,
当时,
当时,
当时,
当时,
当时,
当时,
故答案为:6、8、18.2、25、15、3
(2)17;20km/h;0.1h或5.3h
【知识点】一次函数的图象
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
5.3 一次函数的图象与性质
一、单选题
1.某公司市场营销部的个人月收入与其每月的销售量成一次函数关系,其图象如图所示,由图中给出的信息可知,营销人员没有销售时的收入是( )
A.310元 B.300元 C.290元 D.280元
2.一次函数 的图象大致是( )
A. B.
C. D.
3.下列各点在正比例函数的图象上的是( )
A. B. C. D.
4.已知一次函数(a是常数),若y随x的增大而增大,则a的值可以是( )
A. B. C.0 D.2
5.已知正比例函数的图象经过点,则的值为( )
A.3 B. C. D.
二、填空题
6.如图,一次函数的图象与正比例函数的图象相交于点,已知点的纵坐标是2,则关于的不等式的解集是 .
7.把直线y=2x﹣1向下平移4个单位,所得直线为 .
8.如图,直线和直线相交于,则关于的不等式解集为 .
9.已知y关于x的一次函数,函数图象经过点,则 ;当时,y的最大值是 .
10.直线与轴的交点坐标为 .
11.从,0,1这三个数中,选取两个不同的数作为一次函数的系数k,b,使一次函数的y值随着x的增大而增大,且图象经过一、三、四象限.则一次函数为 .
三、计算题
12.学习函数的时候我们通过列表、描点和连线的步骤画出函数的图象,进而研究函数的性质.请根据学习“一次函数”时积累的经验和方法研究函数的图象和性质,并解决问题.
(1)若,则函数与x轴交点坐标为(_____,0),与y轴交点坐标为(0,____);
(2)若,根据解析式,写出表格中m,n的值;
x … 0 1 2 3 4 …
y … 11 8 m 2 5 n 11 …
______,_____;
(3)在直角坐标系中画出该函数图象;并写出一条函数的性质:______;
(4)一次函数与该函数图象只有一个交点,则_______.
13.已知一次函数.
(1)当k满足什么条件时,图象经过点?
(2)当k满足什么条件时,y随x的增大而增大?
(3)当k满足什么条件时,图象与y轴的交点为?
四、解答题
14.在数学学习中,及时对知识进行归纳和整理是改善学习的重要方法.善于学习的小明在学习了一次方程(组)、一元一次不等式和一次函数后,对照图形,把相关知识归纳整理如下:
一次函数与方程(组)的关系:
一次函数与不等式的关系:
(1)请你根据以上方框中的内容在下面的数字序号后写出相应的结论:
①______________________; ②______________________,
③______________________; ④______________________.
(2)如果点C的坐标为,那么不等式的解集是___________.
15.在平面直角坐标系中,一次函数的图象由函数的图象平移得到,且经过点.
(1)求该一次函数的表达式;
(2)当时,对于x的每一个值,函数的值大于一次函数的值,直接写出n的取值范围.
五、综合题
16.已知正比例函数y=kx.
(1)若函数图象经过第二、四象限,则k的范围是什么?
(2)点(1,-2)在它的图象上,求它的表达式.
17.已知正比例函数y=kx的图象过点P(3,-3).
(1)写出这个正比例函数的函数解析式;
(2)已知点A(a,2)在这个正比例函数的图象上,求a的值.
18.学生社团作为校园文化的重要载体,是培养学生兴趣爱好,扩大求知领域,陶冶思想情操,展示才华智慧的舞台.某中学社团联合举办了“青春汇聚迎盛会,百团奋进正当时”的主题活动,鼓励学生积极参与社团活动.与此同时,学校计划为参加活动的同学购买一批奖品.经了解,购买2个A种奖品和1个B种奖品需花费64元,购买1个A种奖品和4个B种奖品需花费88元.
(1)求A,B两种奖品的单价;
(2)学校需采购两种奖品共60个,且A种奖品的数量大于B种奖品数量的2倍.设购买A种奖品a个,那么如何购买才能使花费最少?最少花费多少元?
六、实践探究题
19.某数学活动小组结合图象设计如下情景:已知家、书店、学校依次在同一条直线上,书店离家8km,学校离家25km,小明从家出发,匀速骑行0.4h到达书店;在书店停留0.6h后,匀速骑行1h到达学校;在学校学习一段时间,然后回家;回家途中,匀速骑行1h后减速,继续匀速骑行回到家.给出的图象反映了这个过程中小明离家的距离与离开家的时间之间的对应关系.
请根据相关信息解答下列问题:
(1)填表:
离开家的时间/h 0.3 0.8 1.6 3 4.5 5.2
离开家的距离/km
(2)填空:
①书店到学校的距离为 km;
②从学校回家途中减速前的骑行速度为 ;
③当小明离家的距离为2km时,他离开家的时间为 .
答案解析部分
1.【答案】B
【知识点】一次函数的图象
2.【答案】D
【知识点】一次函数图象、性质与系数的关系
3.【答案】B
【知识点】正比例函数的性质
4.【答案】D
【知识点】一次函数的性质
5.【答案】A
【知识点】利用开平方求未知数;正比例函数的性质
6.【答案】
【知识点】一次函数与不等式(组)的关系
7.【答案】y=2x﹣5
【知识点】一次函数图象与几何变换
8.【答案】
【知识点】一次函数的图象;一次函数与不等式(组)的关系;比较一次函数值的大小
9.【答案】2;
【知识点】待定系数法求一次函数解析式;一次函数的性质
10.【答案】(0,-5)
【知识点】一次函数图象与坐标轴交点问题
11.【答案】
【知识点】一次函数图象、性质与系数的关系
12.【答案】(1)1,3;
(2)5,8;
(3)当时,y随x的增大而减小;当时,y随x的增大而增大;
(4).
【知识点】一次函数的概念;一次函数图象与坐标轴交点问题;描点法画函数图象
13.【答案】(1)当时,它的图象经过点;
(2)当时,y随x的增大而减增大
(3)当时,图象与y轴的交点为
【知识点】一次函数图象与坐标轴交点问题;一次函数的性质
14.【答案】(1),,,;(2).
【知识点】一次函数与不等式(组)的关系
15.【答案】(1)
(2)
【知识点】待定系数法求一次函数解析式;一次函数与不等式(组)的关系
16.【答案】(1)解:∵函数图象经过第二、四象限,
∴k<0
(2)解:当x=1,y=-2时,则k=-2,
即:y=-2x
【知识点】正比例函数的图象和性质;待定系数法求一次函数解析式
17.【答案】(1)解:代入求值:-3=3k
K=-1
所以解析式是y=-x
(2)解:点 A(a,2)在图像上.
所以,a=-2
【知识点】正比例函数的图象和性质;待定系数法求一次函数解析式
18.【答案】(1)A种奖品的单价为24元,B种奖品的单价为16元
(2)购买A种奖品41个、B种奖品19个时花费最少,最少为1288元
【知识点】二元一次方程组的其他应用;一元一次不等式的应用;一次函数的性质
19.【答案】(1)解:设小明离家的距离为
由图像可知:当,设,将代入得,,即
当,
当,,将代入得
,解得,
当,
当,,将代入得
,解得,
当,,将代入得
,解得,
当时,
当时,
当时,
当时,
当时,
当时,
故答案为:6、8、18.2、25、15、3
(2)17;20km/h;0.1h或5.3h
【知识点】一次函数的图象
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
