2025年秋期苏科版数学(2024)八年级上册第一次月考试题 (含答案)
文档属性
| 名称 | 2025年秋期苏科版数学(2024)八年级上册第一次月考试题 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 516.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-27 05:38:43 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2025年秋期苏科版数学(2024)八年级上册第一次月考试题
一、单选题(共10题;共20分)
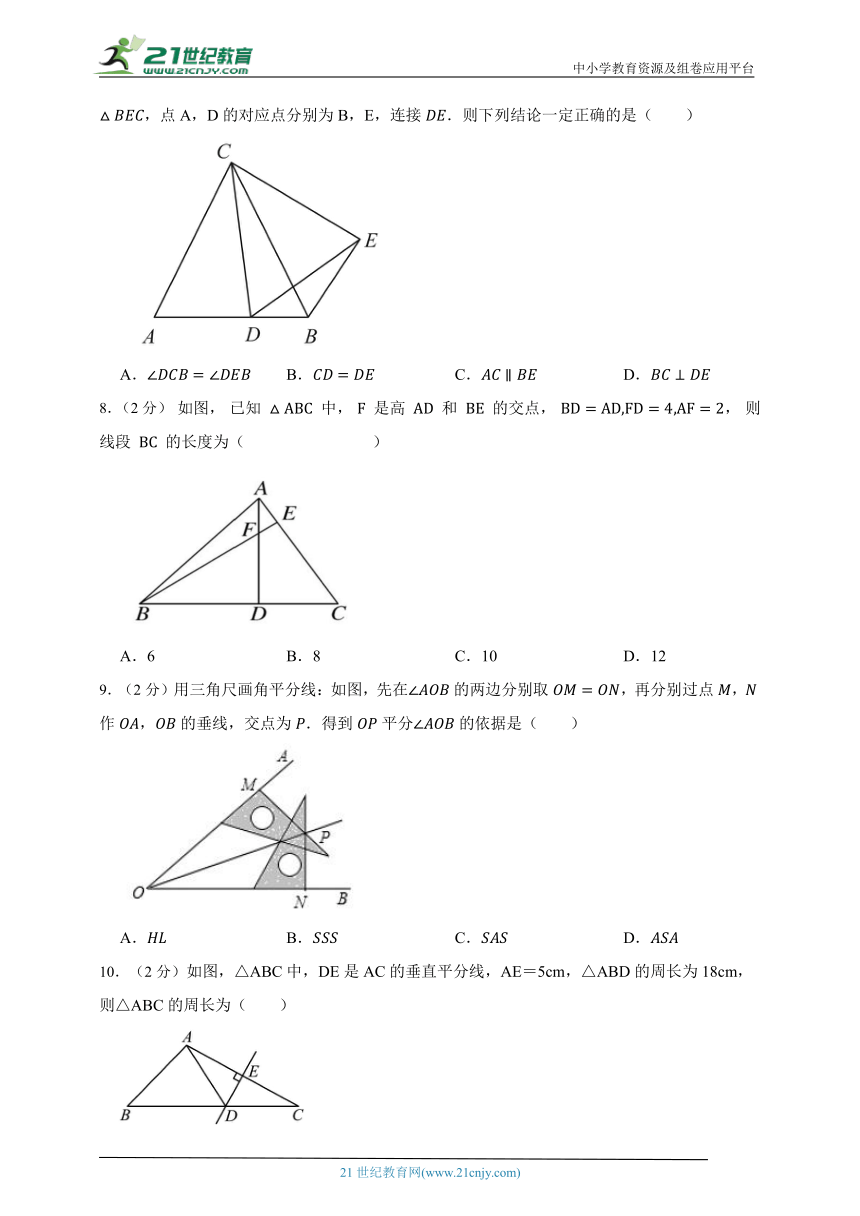
1.(2分)如图,直线DE是ABC边AC的垂直平分线,且与AC相交于点E,与AB相交于点D,连接CD,已知BC=8cm,AB=12cm,则BCD的周长为( )
A.16cm B.18cm C.20cm D.22cm
2.(2分)如图,一条公路修到湖边时需绕道,第一次拐角,第二次拐角,为了保持公路与平行,则第三次拐角的度数应为( )
A. B. C. D.
3.(2分)如用三根木棒首尾相接围成,其中,,则木棒的长可能是( )
A. B. C. D.
4.(2分)如图,若直线,,,则的度数为( )
A. B. C. D.
5.(2分)将下列不同长度的只铅笔首尾顺次连接,能组成三角形的是( ).
A.,, B.,,
C.,, D.,,
6.(2分)中,,,则的度数是( ).
A. B. C. D.
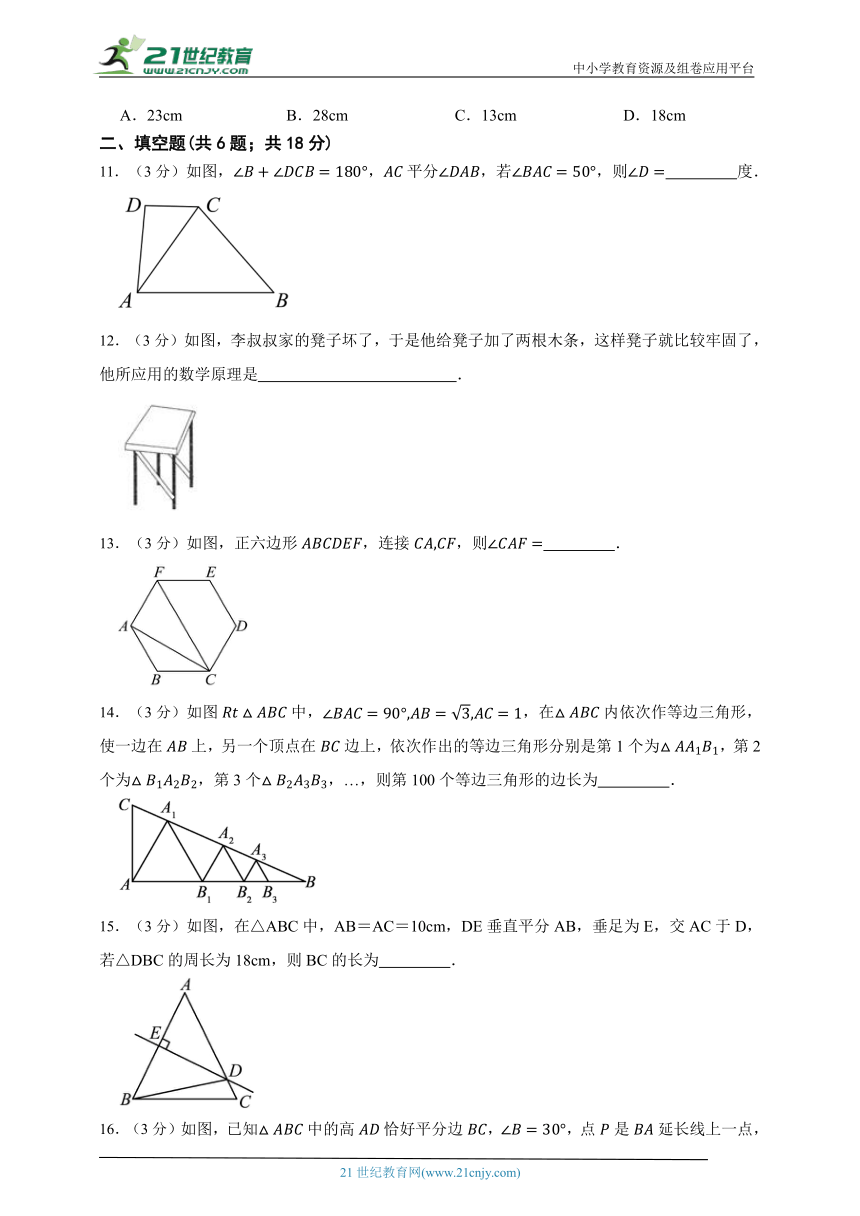
7.(2分)如图,在中,,D为边上一点,将绕点C逆时针旋转得到,点A,D的对应点分别为B,E,连接.则下列结论一定正确的是( )
A. B. C. D.
8.(2分) 如图, 已知 中, 是高 和 的交点, , 则线段 的长度为( )
A.6 B.8 C.10 D.12
9.(2分)用三角尺画角平分线:如图,先在的两边分别取,再分别过点,作,的垂线,交点为.得到平分的依据是( )
A. B. C. D.
10.(2分)如图,△ABC中,DE是AC的垂直平分线,AE=5cm,△ABD的周长为18cm,则△ABC的周长为( )
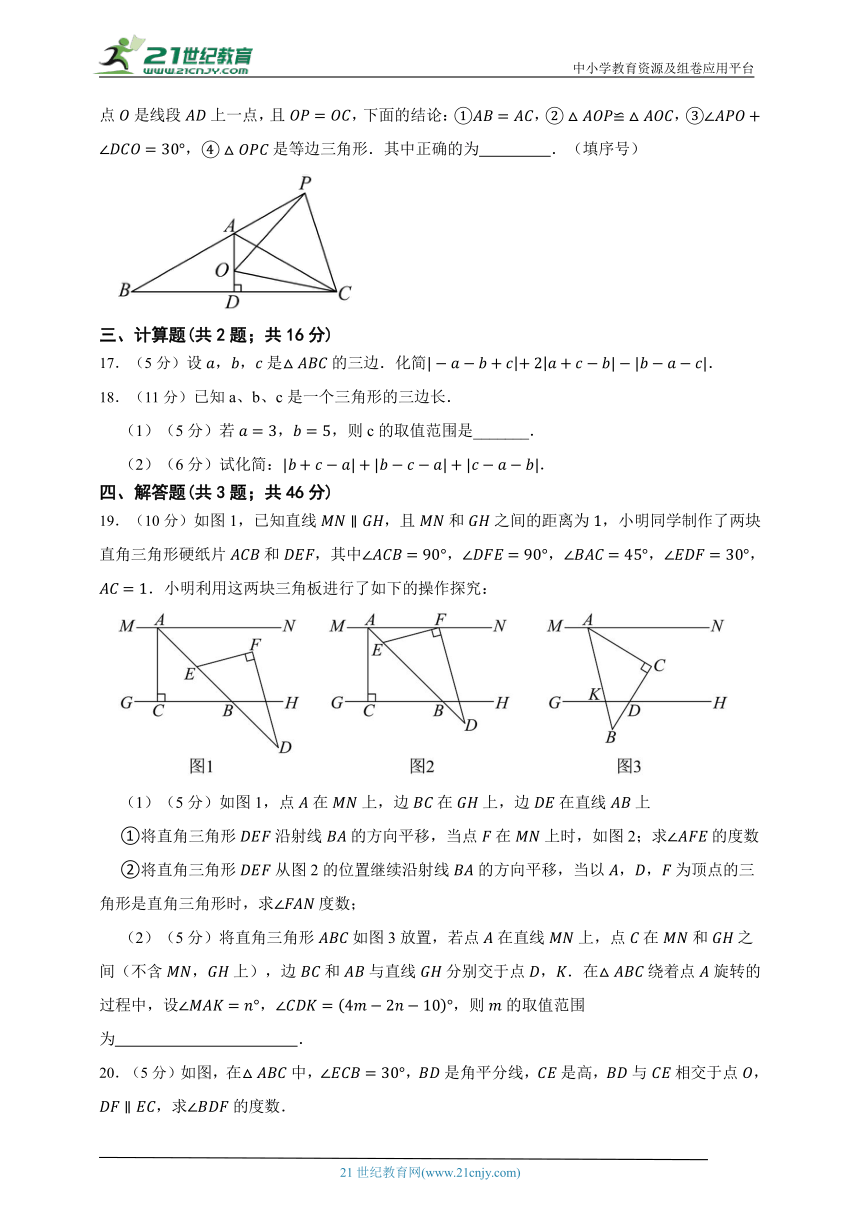
A.23cm B.28cm C.13cm D.18cm
二、填空题(共6题;共18分)
11.(3分)如图,,平分,若,则 度.
12.(3分)如图,李叔叔家的凳子坏了,于是他给凳子加了两根木条,这样凳子就比较牢固了,他所应用的数学原理是 .
13.(3分)如图,正六边形,连接,则 .
14.(3分)如图中,,在内依次作等边三角形,使一边在上,另一个顶点在边上,依次作出的等边三角形分别是第1个为,第2个为,第3个,…,则第100个等边三角形的边长为 .
15.(3分)如图,在△ABC中,AB=AC=10cm,DE垂直平分AB,垂足为E,交AC于D,若△DBC的周长为18cm,则BC的长为 .
16.(3分)如图,已知中的高恰好平分边,,点是延长线上一点,点是线段上一点,且,下面的结论:,,,是等边三角形.其中正确的为 .(填序号)
三、计算题(共2题;共16分)
17.(5分)设,,是的三边.化简.
18.(11分)已知a、b、c是一个三角形的三边长.
(1)(5分)若,,则c的取值范围是_______.
(2)(6分)试化简:.
四、解答题(共3题;共46分)
19.(10分)如图1,已知直线,且和之间的距离为,小明同学制作了两块直角三角形硬纸片和,其中,,,,.小明利用这两块三角板进行了如下的操作探究:
(1)(5分)如图1,点在上,边在上,边在直线上
①将直角三角形沿射线的方向平移,当点在上时,如图2;求的度数
②将直角三角形从图2的位置继续沿射线的方向平移,当以,,为顶点的三角形是直角三角形时,求度数;
(2)(5分)将直角三角形如图3放置,若点在直线上,点在和之间(不含,上),边和与直线分别交于点,.在绕着点旋转的过程中,设,,则的取值范围为 .
20.(5分)如图,在中,,是角平分线,是高,与相交于点,,求的度数.
解:是高(已知),
______(三角形高的定义)
在中,______°(______ )
是角平分线,______=______(角平分线定义),
是的外角,
______=______°
∵(已知)
______=______°(______ )
21.(31分)(1)(15分)问题背景:如图,已知中,,,直线经过点,直线,直线,垂足分别为点,,易证: ;用,,填空
(2)(8分)拓展延伸:如图,将中的条件改为:在中,,,,三点都在直线上,并且有,请求出,,三条线段的数量关系,并证明;
(3)(8分)实际应用:如图,在中,,,点的坐标为,点的坐标为,请直接写出点的坐标.
答案解析部分
1.【答案】C
【知识点】线段垂直平分线的性质
2.【答案】C
【知识点】平行线的性质;三角形外角的概念及性质
3.【答案】C
【知识点】三角形三边关系
4.【答案】D
【知识点】平行线的性质;两直线平行,同位角相等;三角形的外角和
5.【答案】D
【知识点】三角形三边关系
6.【答案】D
【知识点】三角形内角和定理
7.【答案】A
【知识点】三角形全等及其性质;等腰三角形的判定与性质;旋转的性质
8.【答案】C
【知识点】三角形全等的判定-ASA
9.【答案】A
【知识点】直角三角形全等的判定-HL
10.【答案】B
【知识点】线段垂直平分线的性质
11.【答案】80
【知识点】平行线的判定与性质;角平分线的性质
12.【答案】根据三角形稳定性解答
【知识点】三角形的稳定性
13.【答案】
【知识点】等腰三角形的性质;多边形内角与外角
14.【答案】
【知识点】等边三角形的性质;含30°角的直角三角形
15.【答案】8cm
【知识点】线段垂直平分线的性质
16.【答案】
【知识点】线段垂直平分线的性质;等腰三角形的性质;等边三角形的判定;三角形全等的判定-SAS
17.【答案】
【知识点】三角形三边关系
18.【答案】(1)
(2)
【知识点】三角形三边关系;化简含绝对值有理数
19.【答案】(1);的度数为或
(2)
【知识点】三角形内角和定理;三角形外角的概念及性质;含30°角的直角三角形;一元一次方程的实际应用-几何问题
20.【答案】;;三角形内角和;;;;;;120;两直线平行,同位角相等
【知识点】三角形内角和定理;三角形外角的概念及性质;同位角的概念
21.【答案】(1)DE;BD;CE
(2),
证明:在中,,
,,
.
在和中,
≌,
,,
;
(3)点的坐标为.
【知识点】三角形内角和定理;三角形全等及其性质;三角形全等的判定
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025年秋期苏科版数学(2024)八年级上册第一次月考试题
一、单选题(共10题;共20分)
1.(2分)如图,直线DE是ABC边AC的垂直平分线,且与AC相交于点E,与AB相交于点D,连接CD,已知BC=8cm,AB=12cm,则BCD的周长为( )
A.16cm B.18cm C.20cm D.22cm
2.(2分)如图,一条公路修到湖边时需绕道,第一次拐角,第二次拐角,为了保持公路与平行,则第三次拐角的度数应为( )
A. B. C. D.
3.(2分)如用三根木棒首尾相接围成,其中,,则木棒的长可能是( )
A. B. C. D.
4.(2分)如图,若直线,,,则的度数为( )
A. B. C. D.
5.(2分)将下列不同长度的只铅笔首尾顺次连接,能组成三角形的是( ).
A.,, B.,,
C.,, D.,,
6.(2分)中,,,则的度数是( ).
A. B. C. D.
7.(2分)如图,在中,,D为边上一点,将绕点C逆时针旋转得到,点A,D的对应点分别为B,E,连接.则下列结论一定正确的是( )
A. B. C. D.
8.(2分) 如图, 已知 中, 是高 和 的交点, , 则线段 的长度为( )
A.6 B.8 C.10 D.12
9.(2分)用三角尺画角平分线:如图,先在的两边分别取,再分别过点,作,的垂线,交点为.得到平分的依据是( )
A. B. C. D.
10.(2分)如图,△ABC中,DE是AC的垂直平分线,AE=5cm,△ABD的周长为18cm,则△ABC的周长为( )
A.23cm B.28cm C.13cm D.18cm
二、填空题(共6题;共18分)
11.(3分)如图,,平分,若,则 度.
12.(3分)如图,李叔叔家的凳子坏了,于是他给凳子加了两根木条,这样凳子就比较牢固了,他所应用的数学原理是 .
13.(3分)如图,正六边形,连接,则 .
14.(3分)如图中,,在内依次作等边三角形,使一边在上,另一个顶点在边上,依次作出的等边三角形分别是第1个为,第2个为,第3个,…,则第100个等边三角形的边长为 .
15.(3分)如图,在△ABC中,AB=AC=10cm,DE垂直平分AB,垂足为E,交AC于D,若△DBC的周长为18cm,则BC的长为 .
16.(3分)如图,已知中的高恰好平分边,,点是延长线上一点,点是线段上一点,且,下面的结论:,,,是等边三角形.其中正确的为 .(填序号)
三、计算题(共2题;共16分)
17.(5分)设,,是的三边.化简.
18.(11分)已知a、b、c是一个三角形的三边长.
(1)(5分)若,,则c的取值范围是_______.
(2)(6分)试化简:.
四、解答题(共3题;共46分)
19.(10分)如图1,已知直线,且和之间的距离为,小明同学制作了两块直角三角形硬纸片和,其中,,,,.小明利用这两块三角板进行了如下的操作探究:
(1)(5分)如图1,点在上,边在上,边在直线上
①将直角三角形沿射线的方向平移,当点在上时,如图2;求的度数
②将直角三角形从图2的位置继续沿射线的方向平移,当以,,为顶点的三角形是直角三角形时,求度数;
(2)(5分)将直角三角形如图3放置,若点在直线上,点在和之间(不含,上),边和与直线分别交于点,.在绕着点旋转的过程中,设,,则的取值范围为 .
20.(5分)如图,在中,,是角平分线,是高,与相交于点,,求的度数.
解:是高(已知),
______(三角形高的定义)
在中,______°(______ )
是角平分线,______=______(角平分线定义),
是的外角,
______=______°
∵(已知)
______=______°(______ )
21.(31分)(1)(15分)问题背景:如图,已知中,,,直线经过点,直线,直线,垂足分别为点,,易证: ;用,,填空
(2)(8分)拓展延伸:如图,将中的条件改为:在中,,,,三点都在直线上,并且有,请求出,,三条线段的数量关系,并证明;
(3)(8分)实际应用:如图,在中,,,点的坐标为,点的坐标为,请直接写出点的坐标.
答案解析部分
1.【答案】C
【知识点】线段垂直平分线的性质
2.【答案】C
【知识点】平行线的性质;三角形外角的概念及性质
3.【答案】C
【知识点】三角形三边关系
4.【答案】D
【知识点】平行线的性质;两直线平行,同位角相等;三角形的外角和
5.【答案】D
【知识点】三角形三边关系
6.【答案】D
【知识点】三角形内角和定理
7.【答案】A
【知识点】三角形全等及其性质;等腰三角形的判定与性质;旋转的性质
8.【答案】C
【知识点】三角形全等的判定-ASA
9.【答案】A
【知识点】直角三角形全等的判定-HL
10.【答案】B
【知识点】线段垂直平分线的性质
11.【答案】80
【知识点】平行线的判定与性质;角平分线的性质
12.【答案】根据三角形稳定性解答
【知识点】三角形的稳定性
13.【答案】
【知识点】等腰三角形的性质;多边形内角与外角
14.【答案】
【知识点】等边三角形的性质;含30°角的直角三角形
15.【答案】8cm
【知识点】线段垂直平分线的性质
16.【答案】
【知识点】线段垂直平分线的性质;等腰三角形的性质;等边三角形的判定;三角形全等的判定-SAS
17.【答案】
【知识点】三角形三边关系
18.【答案】(1)
(2)
【知识点】三角形三边关系;化简含绝对值有理数
19.【答案】(1);的度数为或
(2)
【知识点】三角形内角和定理;三角形外角的概念及性质;含30°角的直角三角形;一元一次方程的实际应用-几何问题
20.【答案】;;三角形内角和;;;;;;120;两直线平行,同位角相等
【知识点】三角形内角和定理;三角形外角的概念及性质;同位角的概念
21.【答案】(1)DE;BD;CE
(2),
证明:在中,,
,,
.
在和中,
≌,
,,
;
(3)点的坐标为.
【知识点】三角形内角和定理;三角形全等及其性质;三角形全等的判定
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
