第3章 勾股定理 同步练习(含答案)
文档属性
| 名称 | 第3章 勾股定理 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 472.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-27 05:42:57 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第3章 勾股定理
一、单选题
1.在中,a,b,c分别是,,的对边,若,则这个三角形一定是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰直角三角形
2.如图,中,,是的平分线,,垂足为E.若,,则的长度为( )
A. B. C.4 D.2
3.直角三角形的两直角边的长分别为5和12,则斜边上的中线长是( )
A.17 B.13 C.8.5 D.6.5
4.如图,△ABC和△DCE都是边长为3的等边三角形,点B,C,E在同一条直线上,连接BD,则BD长( )
A. B.2 C.3 D.4
5.满足下列条件的不是直角三角形的是( )
A. B.,,
C. D.,,
6.如图,小明为了测量河宽,先在延长线上取一点,再在同岸取一点,使,测得,,,那么河宽为( )
A. B. C. D.
7.如图,在 中, , , , 绕点 顺时针旋转得到 ,当点 落在 边上时,连接 ,取 的中点 ,连接 ,则 的长是( )
A. B. C.3 D.
8.如图,在中,,.分别以、为圆心,以大于的长为半径作弧,两弧分别交于、两点,连接直线,分别交、于点、,连接,则的面积为( )
A.10 B.12 C.14 D.16
9.如图,是等边内一点,,,,将线段以点为旋转中心逆时针旋转得到线段,则的度数为( )
A. B. C. D.
10.已知△ABC的三个内角分别为∠A、∠B、∠C,三边分别为a、b、c,下列条件不能判定△ABC是直角三角形的是( )
A.∠A:∠B:∠C=3:4:7 B.∠A=∠B-∠C
C.a:b:c=2:3:4 D.b2=(a+c) (a-c)
二、填空题
11.如图,在中,,分别以,,为直径作半圆,它们的面积分别记为,,,若,则 .
12.如图,长的梯子靠在墙上,梯子的底端离墙脚线的距离为,则梯子顶端距离地面的高度为 .
13.如图,,,边上的中线,则的面积为 .
14.若3,4,a和5,b,13是两组勾股数,则a+b的值是 .
15.如图,在中,,点,在线段上,且,将线段绕点顺时针旋转后得到线段,连接,.给出以下结论:
①;
②;
③;
④.
其中正确的是 .(写出所有正确结论的序号)
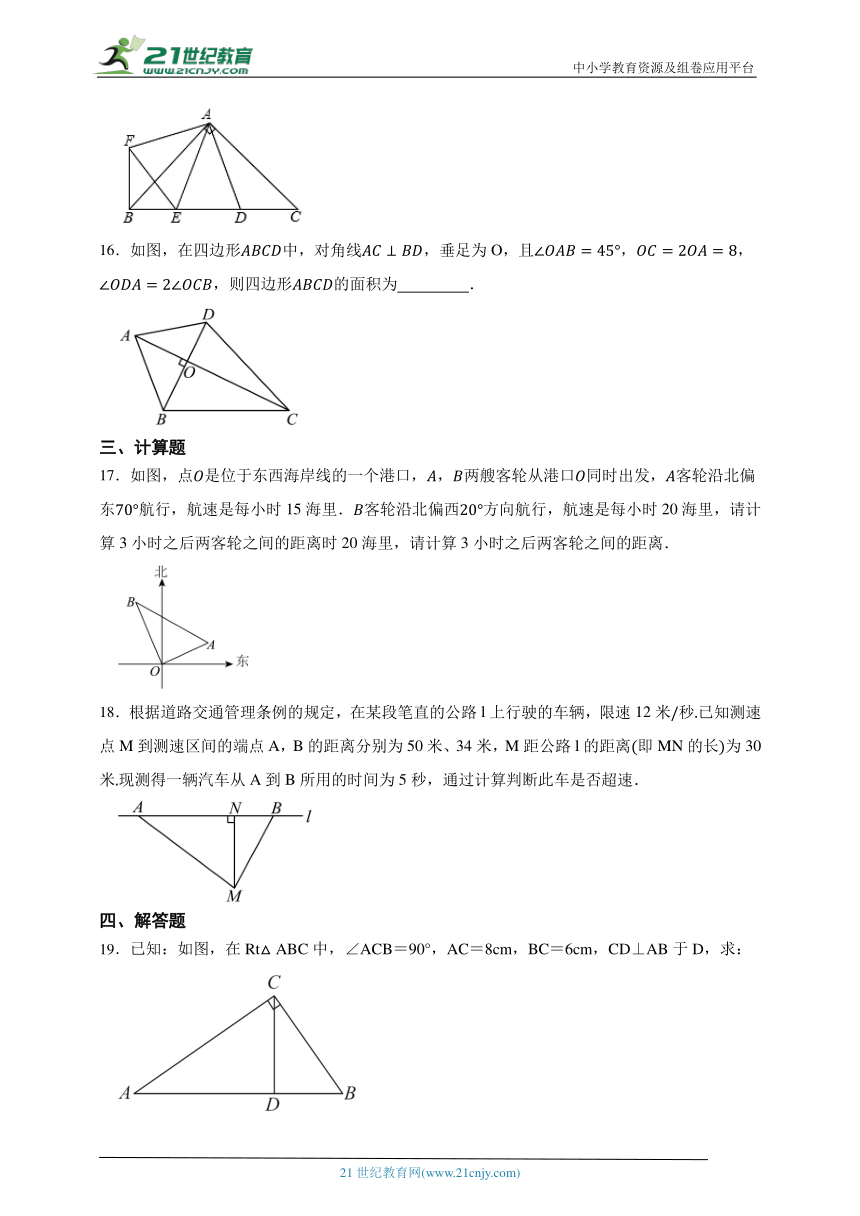
16.如图,在四边形中,对角线,垂足为O,且,,,则四边形的面积为 .
三、计算题
17.如图,点是位于东西海岸线的一个港口,,两艘客轮从港口同时出发,客轮沿北偏东航行,航速是每小时15海里.客轮沿北偏西方向航行,航速是每小时20海里,请计算3小时之后两客轮之间的距离时20海里,请计算3小时之后两客轮之间的距离.
18.根据道路交通管理条例的规定,在某段笔直的公路l上行驶的车辆,限速12米秒已知测速点M到测速区间的端点A,B的距离分别为50米、34米,M距公路l的距离即MN的长为30米现测得一辆汽车从A到B所用的时间为5秒,通过计算判断此车是否超速.
四、解答题
19.已知:如图,在Rt△ABC中,∠ACB=90°,AC=8cm,BC=6cm,CD⊥AB于D,求:
(1)斜边AB的长;
(2)高CD的长.
20.如图,我军巡逻艇正在处巡逻,突然发现在南偏东方向距离12海里的处有一艘走私船,以18海里/小时的速度沿南偏西方向行驶,我军巡逻艇立刻沿直线追赶,半小时后在点处将其追上,求我军巡逻艇的航行速度是多少?
21.《九章算术》中“勾股”一章有记载:今有池方一丈,葭生其中央,出水一尺.引葭赴岸,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它的顶端恰好到达池边的水面,求芦苇的长度.(1丈=10尺)
解决下列问题:
(1)示意图中,线段AF的长为 尺,线段EF的长为 尺;
(2)求芦苇的长度.
答案解析部分
1.【答案】B
【知识点】勾股定理;算术平方根的性质(双重非负性);绝对值的非负性
2.【答案】C
【知识点】直角三角形全等的判定-HL;角平分线的性质;勾股定理
3.【答案】D
【知识点】勾股定理;直角三角形斜边上的中线
4.【答案】C
【知识点】等边三角形的性质;勾股定理
5.【答案】A
【知识点】三角形内角和定理;勾股定理的逆定理
6.【答案】B
【知识点】三角形外角的概念及性质;等腰三角形的判定;含30°角的直角三角形;勾股定理
7.【答案】A
【知识点】勾股定理;旋转的性质
8.【答案】B
【知识点】三角形的面积;线段垂直平分线的性质;等腰三角形的性质;勾股定理
9.【答案】D
【知识点】等边三角形的判定与性质;勾股定理的逆定理;旋转的性质;三角形全等的判定-SAS
10.【答案】C
【知识点】三角形内角和定理;勾股定理的逆定理
11.【答案】
【知识点】勾股定理
12.【答案】
【知识点】勾股定理
13.【答案】6
【知识点】勾股定理的逆定理;三角形全等的判定-SAS
14.【答案】17
【知识点】勾股数
15.【答案】①③④
【知识点】三角形全等及其性质;勾股定理;旋转的性质
16.【答案】42
【知识点】等腰三角形的判定与性质;勾股定理;三角形全等的判定-SAS
17.【答案】3小时之后两客轮之间的距离为海里
【知识点】勾股定理的实际应用-(行驶、航行)方向问题
18.【答案】此车没有超速.
【知识点】勾股定理
19.【答案】(1)10cm
(2)4.8cm
【知识点】三角形的角平分线、中线和高;勾股定理
20.【答案】海里/小时
【知识点】勾股定理的实际应用-(行驶、航行)方向问题
21.【答案】(1)5,1;(2)芦苇长13尺.
【知识点】勾股定理的应用
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第3章 勾股定理
一、单选题
1.在中,a,b,c分别是,,的对边,若,则这个三角形一定是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰直角三角形
2.如图,中,,是的平分线,,垂足为E.若,,则的长度为( )
A. B. C.4 D.2
3.直角三角形的两直角边的长分别为5和12,则斜边上的中线长是( )
A.17 B.13 C.8.5 D.6.5
4.如图,△ABC和△DCE都是边长为3的等边三角形,点B,C,E在同一条直线上,连接BD,则BD长( )
A. B.2 C.3 D.4
5.满足下列条件的不是直角三角形的是( )
A. B.,,
C. D.,,
6.如图,小明为了测量河宽,先在延长线上取一点,再在同岸取一点,使,测得,,,那么河宽为( )
A. B. C. D.
7.如图,在 中, , , , 绕点 顺时针旋转得到 ,当点 落在 边上时,连接 ,取 的中点 ,连接 ,则 的长是( )
A. B. C.3 D.
8.如图,在中,,.分别以、为圆心,以大于的长为半径作弧,两弧分别交于、两点,连接直线,分别交、于点、,连接,则的面积为( )
A.10 B.12 C.14 D.16
9.如图,是等边内一点,,,,将线段以点为旋转中心逆时针旋转得到线段,则的度数为( )
A. B. C. D.
10.已知△ABC的三个内角分别为∠A、∠B、∠C,三边分别为a、b、c,下列条件不能判定△ABC是直角三角形的是( )
A.∠A:∠B:∠C=3:4:7 B.∠A=∠B-∠C
C.a:b:c=2:3:4 D.b2=(a+c) (a-c)
二、填空题
11.如图,在中,,分别以,,为直径作半圆,它们的面积分别记为,,,若,则 .
12.如图,长的梯子靠在墙上,梯子的底端离墙脚线的距离为,则梯子顶端距离地面的高度为 .
13.如图,,,边上的中线,则的面积为 .
14.若3,4,a和5,b,13是两组勾股数,则a+b的值是 .
15.如图,在中,,点,在线段上,且,将线段绕点顺时针旋转后得到线段,连接,.给出以下结论:
①;
②;
③;
④.
其中正确的是 .(写出所有正确结论的序号)
16.如图,在四边形中,对角线,垂足为O,且,,,则四边形的面积为 .
三、计算题
17.如图,点是位于东西海岸线的一个港口,,两艘客轮从港口同时出发,客轮沿北偏东航行,航速是每小时15海里.客轮沿北偏西方向航行,航速是每小时20海里,请计算3小时之后两客轮之间的距离时20海里,请计算3小时之后两客轮之间的距离.
18.根据道路交通管理条例的规定,在某段笔直的公路l上行驶的车辆,限速12米秒已知测速点M到测速区间的端点A,B的距离分别为50米、34米,M距公路l的距离即MN的长为30米现测得一辆汽车从A到B所用的时间为5秒,通过计算判断此车是否超速.
四、解答题
19.已知:如图,在Rt△ABC中,∠ACB=90°,AC=8cm,BC=6cm,CD⊥AB于D,求:
(1)斜边AB的长;
(2)高CD的长.
20.如图,我军巡逻艇正在处巡逻,突然发现在南偏东方向距离12海里的处有一艘走私船,以18海里/小时的速度沿南偏西方向行驶,我军巡逻艇立刻沿直线追赶,半小时后在点处将其追上,求我军巡逻艇的航行速度是多少?
21.《九章算术》中“勾股”一章有记载:今有池方一丈,葭生其中央,出水一尺.引葭赴岸,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它的顶端恰好到达池边的水面,求芦苇的长度.(1丈=10尺)
解决下列问题:
(1)示意图中,线段AF的长为 尺,线段EF的长为 尺;
(2)求芦苇的长度.
答案解析部分
1.【答案】B
【知识点】勾股定理;算术平方根的性质(双重非负性);绝对值的非负性
2.【答案】C
【知识点】直角三角形全等的判定-HL;角平分线的性质;勾股定理
3.【答案】D
【知识点】勾股定理;直角三角形斜边上的中线
4.【答案】C
【知识点】等边三角形的性质;勾股定理
5.【答案】A
【知识点】三角形内角和定理;勾股定理的逆定理
6.【答案】B
【知识点】三角形外角的概念及性质;等腰三角形的判定;含30°角的直角三角形;勾股定理
7.【答案】A
【知识点】勾股定理;旋转的性质
8.【答案】B
【知识点】三角形的面积;线段垂直平分线的性质;等腰三角形的性质;勾股定理
9.【答案】D
【知识点】等边三角形的判定与性质;勾股定理的逆定理;旋转的性质;三角形全等的判定-SAS
10.【答案】C
【知识点】三角形内角和定理;勾股定理的逆定理
11.【答案】
【知识点】勾股定理
12.【答案】
【知识点】勾股定理
13.【答案】6
【知识点】勾股定理的逆定理;三角形全等的判定-SAS
14.【答案】17
【知识点】勾股数
15.【答案】①③④
【知识点】三角形全等及其性质;勾股定理;旋转的性质
16.【答案】42
【知识点】等腰三角形的判定与性质;勾股定理;三角形全等的判定-SAS
17.【答案】3小时之后两客轮之间的距离为海里
【知识点】勾股定理的实际应用-(行驶、航行)方向问题
18.【答案】此车没有超速.
【知识点】勾股定理
19.【答案】(1)10cm
(2)4.8cm
【知识点】三角形的角平分线、中线和高;勾股定理
20.【答案】海里/小时
【知识点】勾股定理的实际应用-(行驶、航行)方向问题
21.【答案】(1)5,1;(2)芦苇长13尺.
【知识点】勾股定理的应用
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
