1.1 三角形中的线段和角 同步练习(含答案)
文档属性
| 名称 | 1.1 三角形中的线段和角 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 442.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-27 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
1.1 三角形中的线段和角
一、单选题
1.如图,在Rt△ABC中,∠B=90°,D是BC延长线上一点,∠ACD=130°,则∠A等于( )
A.40° B.50° C.65° D.90°
2.如图,中,与的平分线交于点,已知,则的度数是( )
A. B. C. D.
3.若长度分别为a,3,5的三条线段能组成一个三角形,则下列选项中符合条件的a值是( )
A.1 B.2 C.3 D.9
4.下列每组数分别表示三根木棒的长度,能摆成三角形的一组是( )
A. B.
C. D.
5.如图,∠A=40°,∠CBD是ABC的外角,∠CBD=110°,则∠C的大小( )
A.40° B.50° C.70° D.90°
二、判断题
6.三角形的外角和等于与它相邻的两个内角的和
7.用三根长度分别是3厘米、4厘米、5厘米的小棒,能围成一个三角形.( )
8.一个三角形内角和是,把它分成两个小三角形,则每个小三角形的内角和都是.
9.有长度分别为、、、的小棒各一根,从中任选3根小棒都能围成一个三角形.
三、填空题
10.已知中,,,过点A作的高,则 .
11.如图,已知AE是BC边上的中线,△ABC的面积是16,则△AEC的面积是 .
12.如图,在中,是边上的中线,已知,,则和的周长差为 cm.
13.如图,在中,G为的重心,连,则 .
14.一个三角形的边长均为整数,若两边长分别为1和2,则第三边长是 .
15.如图,已知中,,是中线,,,则的面积为 .
四、计算题
16.如图,在中,E是中线的中点,的面积是1,求的面积.
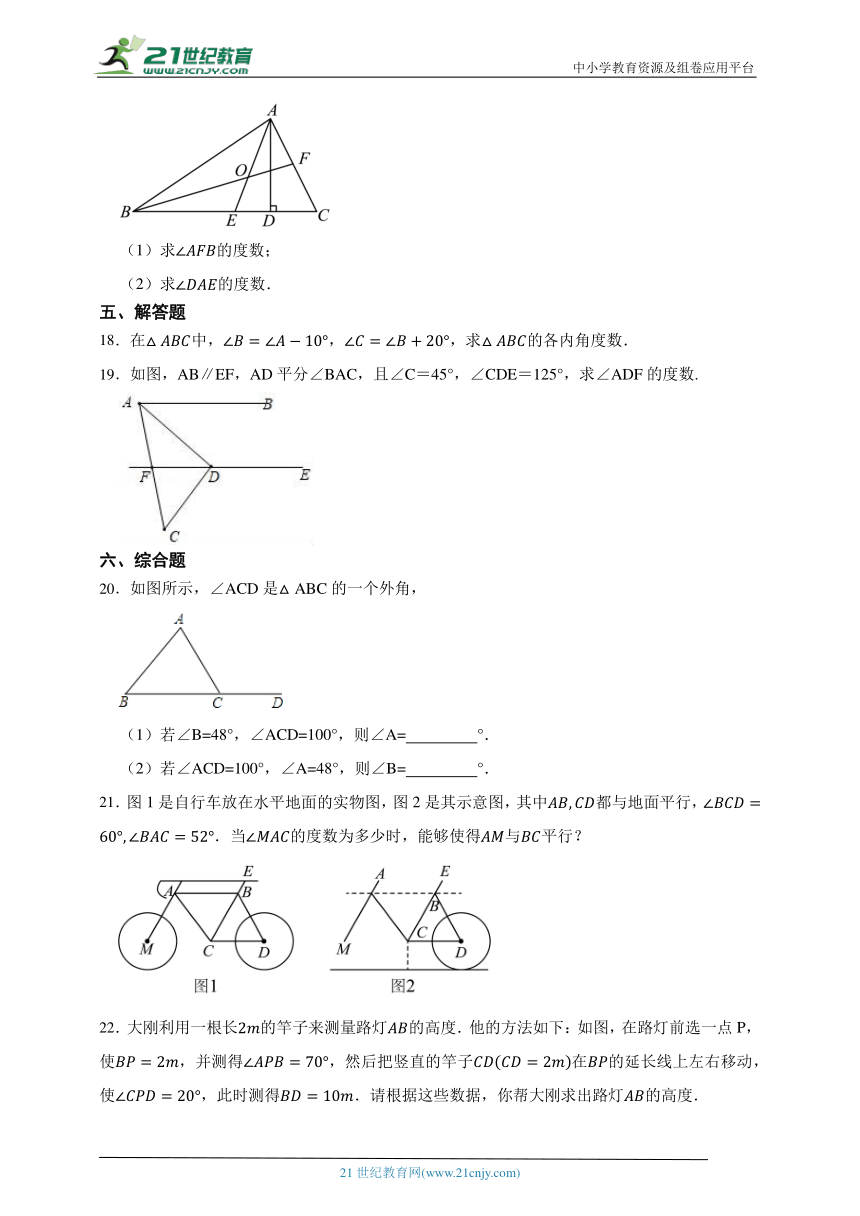
17.已知:如图,中,、分别是的高和角平分线.是的平分线,与交于,若,.
(1)求的度数;
(2)求的度数.
五、解答题
18.在中,,,求的各内角度数.
19.如图,AB∥EF,AD平分∠BAC,且∠C=45°,∠CDE=125°,求∠ADF的度数.
六、综合题
20.如图所示,∠ACD是△ABC的一个外角,
(1)若∠B=48°,∠ACD=100°,则∠A= °.
(2)若∠ACD=100°,∠A=48°,则∠B= °.
21.图1是自行车放在水平地面的实物图,图2是其示意图,其中都与地面平行,.当的度数为多少时,能够使得与平行?
22.大刚利用一根长的竿子来测量路灯的高度.他的方法如下:如图,在路灯前选一点P,使,并测得,然后把竖直的竿子在的延长线上左右移动,使,此时测得.请根据这些数据,你帮大刚求出路灯的高度.
七、实践探究题
23.在中,,平分,P为线段上的一个动点,交直线于E,其夹角记为.
(1)如图,,,求的度数;
(2)探究与,的数量关系.
答案解析部分
1.【答案】A
【知识点】三角形外角的概念及性质
2.【答案】B
【知识点】三角形内角和定理
3.【答案】C
【知识点】三角形三边关系
4.【答案】C
【知识点】三角形三边关系
5.【答案】C
【知识点】三角形外角的概念及性质
6.【答案】错误
【知识点】三角形外角的概念及性质
7.【答案】正确
【知识点】三角形三边关系
8.【答案】
【知识点】三角形内角和定理
9.【答案】错误
【知识点】三角形三边关系
10.【答案】或
【知识点】角的运算;三角形的角平分线、中线和高;三角形相关概念
11.【答案】8
【知识点】三角形的角平分线、中线和高;三角形的面积
12.【答案】2
【知识点】三角形的角平分线、中线和高
13.【答案】
【知识点】三角形的角平分线、中线和高;三角形的重心及应用
14.【答案】2
【知识点】三角形三边关系
15.【答案】6
【知识点】三角形的角平分线、中线和高
16.【答案】
【知识点】三角形的角平分线、中线和高
17.【答案】(1)
(2)
【知识点】三角形内角和定理
18.【答案】,,
【知识点】三角形内角和定理
19.【答案】解:∵∠CDE=125°,∠C=45°,
∴∠CFD=∠CDE﹣∠C=125°﹣45°=80°,
∵AB∥EF,
∴∠BAC=∠DFC=80°,
∵AD平分∠BAC,
∴∠FAD= ∠BAC=40°,
∴∠ADF=∠DFC﹣∠DAF=40°
【知识点】平行线的性质;三角形外角的概念及性质
20.【答案】(1)52
(2)52
【知识点】三角形外角的概念及性质
21.【答案】当时,
【知识点】平行线的判定与性质;三角形内角和定理
22.【答案】路灯的高度是
【知识点】三角形内角和定理
23.【答案】(1)
(2)
【知识点】三角形内角和定理;三角形外角的概念及性质
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
1.1 三角形中的线段和角
一、单选题
1.如图,在Rt△ABC中,∠B=90°,D是BC延长线上一点,∠ACD=130°,则∠A等于( )
A.40° B.50° C.65° D.90°
2.如图,中,与的平分线交于点,已知,则的度数是( )
A. B. C. D.
3.若长度分别为a,3,5的三条线段能组成一个三角形,则下列选项中符合条件的a值是( )
A.1 B.2 C.3 D.9
4.下列每组数分别表示三根木棒的长度,能摆成三角形的一组是( )
A. B.
C. D.
5.如图,∠A=40°,∠CBD是ABC的外角,∠CBD=110°,则∠C的大小( )
A.40° B.50° C.70° D.90°
二、判断题
6.三角形的外角和等于与它相邻的两个内角的和
7.用三根长度分别是3厘米、4厘米、5厘米的小棒,能围成一个三角形.( )
8.一个三角形内角和是,把它分成两个小三角形,则每个小三角形的内角和都是.
9.有长度分别为、、、的小棒各一根,从中任选3根小棒都能围成一个三角形.
三、填空题
10.已知中,,,过点A作的高,则 .
11.如图,已知AE是BC边上的中线,△ABC的面积是16,则△AEC的面积是 .
12.如图,在中,是边上的中线,已知,,则和的周长差为 cm.
13.如图,在中,G为的重心,连,则 .
14.一个三角形的边长均为整数,若两边长分别为1和2,则第三边长是 .
15.如图,已知中,,是中线,,,则的面积为 .
四、计算题
16.如图,在中,E是中线的中点,的面积是1,求的面积.
17.已知:如图,中,、分别是的高和角平分线.是的平分线,与交于,若,.
(1)求的度数;
(2)求的度数.
五、解答题
18.在中,,,求的各内角度数.
19.如图,AB∥EF,AD平分∠BAC,且∠C=45°,∠CDE=125°,求∠ADF的度数.
六、综合题
20.如图所示,∠ACD是△ABC的一个外角,
(1)若∠B=48°,∠ACD=100°,则∠A= °.
(2)若∠ACD=100°,∠A=48°,则∠B= °.
21.图1是自行车放在水平地面的实物图,图2是其示意图,其中都与地面平行,.当的度数为多少时,能够使得与平行?
22.大刚利用一根长的竿子来测量路灯的高度.他的方法如下:如图,在路灯前选一点P,使,并测得,然后把竖直的竿子在的延长线上左右移动,使,此时测得.请根据这些数据,你帮大刚求出路灯的高度.
七、实践探究题
23.在中,,平分,P为线段上的一个动点,交直线于E,其夹角记为.
(1)如图,,,求的度数;
(2)探究与,的数量关系.
答案解析部分
1.【答案】A
【知识点】三角形外角的概念及性质
2.【答案】B
【知识点】三角形内角和定理
3.【答案】C
【知识点】三角形三边关系
4.【答案】C
【知识点】三角形三边关系
5.【答案】C
【知识点】三角形外角的概念及性质
6.【答案】错误
【知识点】三角形外角的概念及性质
7.【答案】正确
【知识点】三角形三边关系
8.【答案】
【知识点】三角形内角和定理
9.【答案】错误
【知识点】三角形三边关系
10.【答案】或
【知识点】角的运算;三角形的角平分线、中线和高;三角形相关概念
11.【答案】8
【知识点】三角形的角平分线、中线和高;三角形的面积
12.【答案】2
【知识点】三角形的角平分线、中线和高
13.【答案】
【知识点】三角形的角平分线、中线和高;三角形的重心及应用
14.【答案】2
【知识点】三角形三边关系
15.【答案】6
【知识点】三角形的角平分线、中线和高
16.【答案】
【知识点】三角形的角平分线、中线和高
17.【答案】(1)
(2)
【知识点】三角形内角和定理
18.【答案】,,
【知识点】三角形内角和定理
19.【答案】解:∵∠CDE=125°,∠C=45°,
∴∠CFD=∠CDE﹣∠C=125°﹣45°=80°,
∵AB∥EF,
∴∠BAC=∠DFC=80°,
∵AD平分∠BAC,
∴∠FAD= ∠BAC=40°,
∴∠ADF=∠DFC﹣∠DAF=40°
【知识点】平行线的性质;三角形外角的概念及性质
20.【答案】(1)52
(2)52
【知识点】三角形外角的概念及性质
21.【答案】当时,
【知识点】平行线的判定与性质;三角形内角和定理
22.【答案】路灯的高度是
【知识点】三角形内角和定理
23.【答案】(1)
(2)
【知识点】三角形内角和定理;三角形外角的概念及性质
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
