1.5 等腰三角形 同步练习(含答案)
文档属性
| 名称 | 1.5 等腰三角形 同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 442.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-27 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
1.5 等腰三角形
一、单选题
1.如图,在中,,将绕点A顺时针旋转得到,连接,当点B的对应点落在边上时,的度数为( )
A. B. C. D.
2.如图,在△ABC中,∠A=90°,∠C=30°,∠ABC的角平分线与线段AC相交于点D,若CD=8,则AD的长( )
A.6 B.5 C.4 D.3
3.若等腰三角形的一边长等于6,另一边长等于4,则它的周长等于( )
A.15或17 B.16 C.14 D.14或16
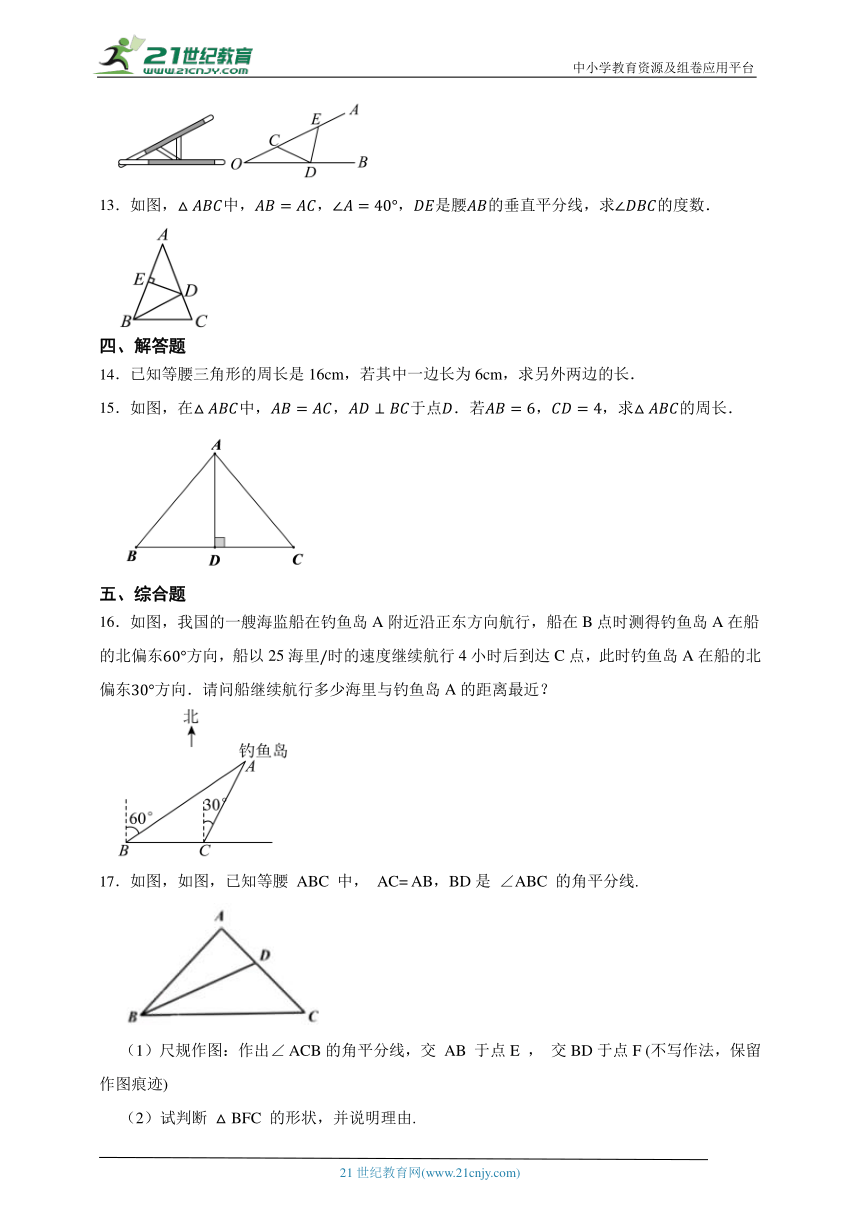
4.如图,△ABC中,AC=BC,直线经过点C,则下列说法正确的是( )
A.l垂直AB B.l平分AB
C.l垂直平分AB D.l与AB的关系不能确定
5.若等腰三角形的一个外角是,则底角是( )
A. B.或 C. D.或
二、填空题
6.已知等腰三角形两边的长为a,b,且满足.则这个等腰三角形的周长为 .
7.如图,在△ABC中,∠ACB=90°,∠ABC=60°,BD平分∠ABC,P点是BD的中点,若AD=10,则CP的长为 .
8.如图,将绕点按顺时针旋转一定角度得到,点的对应点恰好落在边上.
(1)是等腰三角形吗? (选填“是”或“否”);
(2)若,则 度.
9.如图,在中,,,平分,若,则 .
10.如图,将绕点A 逆时针旋转得到,若点D在线段的延长线上,,则旋转角的度数为 .
11.若等腰三角形中有一个角等于40°,则这个等腰三角形的顶角的度数为 .
三、计算题
12.“三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒组成,两根棒在O点相连并可绕O转动、C点固定,,点D、E可在槽中滑动,若,求的度数.
13.如图,中,,,是腰的垂直平分线,求的度数.
四、解答题
14.已知等腰三角形的周长是16cm,若其中一边长为6cm,求另外两边的长.
15.如图,在中,,于点.若,,求的周长.
五、综合题
16.如图,我国的一艘海监船在钓鱼岛A附近沿正东方向航行,船在B点时测得钓鱼岛A在船的北偏东方向,船以25海里时的速度继续航行4小时后到达C点,此时钓鱼岛A在船的北偏东方向.请问船继续航行多少海里与钓鱼岛A的距离最近?
17.如图,如图,已知等腰 ABC 中, AC= AB,BD是 ∠ABC 的角平分线.
(1)尺规作图:作出∠ ACB的角平分线,交 AB 于点E , 交BD于点F (不写作法,保留作图痕迹)
(2)试判断 △BFC 的形状,并说明理由.
18.如图,△ABC是等边三角形,AE=CD,BQ⊥AD于Q,BE交AD于P.
(1)求证:△ABE≌△CAD;
(2)求∠PBQ的度数.
六、实践探究题
19.【概念学习】
规定①:如果一个三角形的三个角分别等于另一个三角形的三个角,那么称这两个三角形互为“形似三角形”.
规定②:从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原来三角形是“形似三角形”,我们把这条线段叫做这个三角形的“等腰分割线”.
(1)【概念理解】
如图1,在△ABC中,∠A=36°,AB=AC,CD平分∠ACB,则△CBD与△ABC (填“是”或“不是”)互为“形似三角形”.
(2)如图2,在△ABC中,CD平分∠ACB,∠A=36°,∠B=48°.求证:CD为△ABC的等腰分割线;
(3)【概念应用】
在△ABC中,∠A=45°,CD是△ABC的等腰分割线,直接写出∠ACB的度数.
答案解析部分
1.【答案】D
【知识点】三角形内角和定理;等腰三角形的性质;旋转的性质
2.【答案】C
【知识点】等腰三角形的判定;含30°角的直角三角形
3.【答案】D
【知识点】等腰三角形的性质
4.【答案】D
【知识点】等腰三角形的性质
5.【答案】A
【知识点】三角形内角和定理;三角形外角的概念及性质;等腰三角形的性质
6.【答案】15
【知识点】三角形三边关系;等腰三角形的概念
7.【答案】5
【知识点】三角形内角和定理;等腰三角形的性质;直角三角形斜边上的中线
8.【答案】是;
【知识点】三角形内角和定理;等腰三角形的判定与性质;旋转的性质
9.【答案】2
【知识点】角平分线的性质;含30°角的直角三角形
10.【答案】
【知识点】等腰三角形的性质;旋转的性质
11.【答案】40°或100°
【知识点】三角形内角和定理;等腰三角形的性质
12.【答案】.
【知识点】三角形内角和定理;三角形外角的概念及性质;等腰三角形的性质
13.【答案】
【知识点】三角形内角和定理;线段垂直平分线的性质;等腰三角形的性质
14.【答案】6cm,4cm或5cm,5cm
【知识点】等腰三角形的判定与性质
15.【答案】
【知识点】等腰三角形的性质
16.【答案】船继续航行50海里与钓鱼岛A的距离最近
【知识点】三角形外角的概念及性质;等腰三角形的判定;含30°角的直角三角形
17.【答案】(1)证明:(1)作图
∴如图所示,CE为所求.
(2)解:△BFC是等腰三角形,理由如下: ∵ AB=AC, ∴∠ABD=∠ACB .
∵BD平分∠ABD,CE平分∠ACB, ∴∠FBC= ∠ABC , ∠FCB= ∠ACB, ∴ ∠FBC=∠FCB,∴BF =CF. 即△BFC是等腰三角形
【知识点】等腰三角形的判定与性质;尺规作图-作角的平分线
18.【答案】(1)证明:∵△ABC是等边三角形,
∴AB=AC,∠BAC=∠C=60°,
在△ABE与△CAD中,
∴△ABE≌△CAD(SAS);
(2)解:由(1)知△ABE≌△CAD,
∴∠ABE=∠CAD,
∴∠BPQ=∠ABE+∠BAP=∠CAD+∠BAP=∠BAC=60°.
∴∠PBQ=90°-∠BPQ=30°.
【知识点】等边三角形的性质;三角形全等的判定-SAS
19.【答案】(1)是
(2)解:∵∠A=36°,∠B=48°,
∴∠ACB=180°-36°-48°=96°,
∵CD平分∠ACB,
∴∠ACD=∠BCD=∠ACB=48°,
∴∠BCD=∠B=∠ACD,
∴△BCD是等腰三角形,
∴∠ADC=∠BCD+∠B=96°,
在△ABC和△ACD中,
∠A=∠A,∠B=∠ACD,∠ACB=∠ADC,
∴△ABC与△ACD互为“形似三角形”
∴CD为△ABC的等腰分割线.
(3)解:105°或112.5°
【知识点】角的运算;三角形内角和定理;等腰三角形的性质
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
1.5 等腰三角形
一、单选题
1.如图,在中,,将绕点A顺时针旋转得到,连接,当点B的对应点落在边上时,的度数为( )
A. B. C. D.
2.如图,在△ABC中,∠A=90°,∠C=30°,∠ABC的角平分线与线段AC相交于点D,若CD=8,则AD的长( )
A.6 B.5 C.4 D.3
3.若等腰三角形的一边长等于6,另一边长等于4,则它的周长等于( )
A.15或17 B.16 C.14 D.14或16
4.如图,△ABC中,AC=BC,直线经过点C,则下列说法正确的是( )
A.l垂直AB B.l平分AB
C.l垂直平分AB D.l与AB的关系不能确定
5.若等腰三角形的一个外角是,则底角是( )
A. B.或 C. D.或
二、填空题
6.已知等腰三角形两边的长为a,b,且满足.则这个等腰三角形的周长为 .
7.如图,在△ABC中,∠ACB=90°,∠ABC=60°,BD平分∠ABC,P点是BD的中点,若AD=10,则CP的长为 .
8.如图,将绕点按顺时针旋转一定角度得到,点的对应点恰好落在边上.
(1)是等腰三角形吗? (选填“是”或“否”);
(2)若,则 度.
9.如图,在中,,,平分,若,则 .
10.如图,将绕点A 逆时针旋转得到,若点D在线段的延长线上,,则旋转角的度数为 .
11.若等腰三角形中有一个角等于40°,则这个等腰三角形的顶角的度数为 .
三、计算题
12.“三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒组成,两根棒在O点相连并可绕O转动、C点固定,,点D、E可在槽中滑动,若,求的度数.
13.如图,中,,,是腰的垂直平分线,求的度数.
四、解答题
14.已知等腰三角形的周长是16cm,若其中一边长为6cm,求另外两边的长.
15.如图,在中,,于点.若,,求的周长.
五、综合题
16.如图,我国的一艘海监船在钓鱼岛A附近沿正东方向航行,船在B点时测得钓鱼岛A在船的北偏东方向,船以25海里时的速度继续航行4小时后到达C点,此时钓鱼岛A在船的北偏东方向.请问船继续航行多少海里与钓鱼岛A的距离最近?
17.如图,如图,已知等腰 ABC 中, AC= AB,BD是 ∠ABC 的角平分线.
(1)尺规作图:作出∠ ACB的角平分线,交 AB 于点E , 交BD于点F (不写作法,保留作图痕迹)
(2)试判断 △BFC 的形状,并说明理由.
18.如图,△ABC是等边三角形,AE=CD,BQ⊥AD于Q,BE交AD于P.
(1)求证:△ABE≌△CAD;
(2)求∠PBQ的度数.
六、实践探究题
19.【概念学习】
规定①:如果一个三角形的三个角分别等于另一个三角形的三个角,那么称这两个三角形互为“形似三角形”.
规定②:从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原来三角形是“形似三角形”,我们把这条线段叫做这个三角形的“等腰分割线”.
(1)【概念理解】
如图1,在△ABC中,∠A=36°,AB=AC,CD平分∠ACB,则△CBD与△ABC (填“是”或“不是”)互为“形似三角形”.
(2)如图2,在△ABC中,CD平分∠ACB,∠A=36°,∠B=48°.求证:CD为△ABC的等腰分割线;
(3)【概念应用】
在△ABC中,∠A=45°,CD是△ABC的等腰分割线,直接写出∠ACB的度数.
答案解析部分
1.【答案】D
【知识点】三角形内角和定理;等腰三角形的性质;旋转的性质
2.【答案】C
【知识点】等腰三角形的判定;含30°角的直角三角形
3.【答案】D
【知识点】等腰三角形的性质
4.【答案】D
【知识点】等腰三角形的性质
5.【答案】A
【知识点】三角形内角和定理;三角形外角的概念及性质;等腰三角形的性质
6.【答案】15
【知识点】三角形三边关系;等腰三角形的概念
7.【答案】5
【知识点】三角形内角和定理;等腰三角形的性质;直角三角形斜边上的中线
8.【答案】是;
【知识点】三角形内角和定理;等腰三角形的判定与性质;旋转的性质
9.【答案】2
【知识点】角平分线的性质;含30°角的直角三角形
10.【答案】
【知识点】等腰三角形的性质;旋转的性质
11.【答案】40°或100°
【知识点】三角形内角和定理;等腰三角形的性质
12.【答案】.
【知识点】三角形内角和定理;三角形外角的概念及性质;等腰三角形的性质
13.【答案】
【知识点】三角形内角和定理;线段垂直平分线的性质;等腰三角形的性质
14.【答案】6cm,4cm或5cm,5cm
【知识点】等腰三角形的判定与性质
15.【答案】
【知识点】等腰三角形的性质
16.【答案】船继续航行50海里与钓鱼岛A的距离最近
【知识点】三角形外角的概念及性质;等腰三角形的判定;含30°角的直角三角形
17.【答案】(1)证明:(1)作图
∴如图所示,CE为所求.
(2)解:△BFC是等腰三角形,理由如下: ∵ AB=AC, ∴∠ABD=∠ACB .
∵BD平分∠ABD,CE平分∠ACB, ∴∠FBC= ∠ABC , ∠FCB= ∠ACB, ∴ ∠FBC=∠FCB,∴BF =CF. 即△BFC是等腰三角形
【知识点】等腰三角形的判定与性质;尺规作图-作角的平分线
18.【答案】(1)证明:∵△ABC是等边三角形,
∴AB=AC,∠BAC=∠C=60°,
在△ABE与△CAD中,
∴△ABE≌△CAD(SAS);
(2)解:由(1)知△ABE≌△CAD,
∴∠ABE=∠CAD,
∴∠BPQ=∠ABE+∠BAP=∠CAD+∠BAP=∠BAC=60°.
∴∠PBQ=90°-∠BPQ=30°.
【知识点】等边三角形的性质;三角形全等的判定-SAS
19.【答案】(1)是
(2)解:∵∠A=36°,∠B=48°,
∴∠ACB=180°-36°-48°=96°,
∵CD平分∠ACB,
∴∠ACD=∠BCD=∠ACB=48°,
∴∠BCD=∠B=∠ACD,
∴△BCD是等腰三角形,
∴∠ADC=∠BCD+∠B=96°,
在△ABC和△ACD中,
∠A=∠A,∠B=∠ACD,∠ACB=∠ADC,
∴△ABC与△ACD互为“形似三角形”
∴CD为△ABC的等腰分割线.
(3)解:105°或112.5°
【知识点】角的运算;三角形内角和定理;等腰三角形的性质
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
