3.1 勾股定理的探究 同步练习(含答案)
文档属性
| 名称 | 3.1 勾股定理的探究 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 595.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-27 05:51:20 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
3.1 勾股定理的探究
一、单选题
1.以直角三角形的三边为边作正方形,三个正方形的面积如图所示,正方形A的面积为( )
A.6 B.36 C.64 D.
2.一个直角三角形的两条直角边分别为和,则第三边长是( )
A.3 B.4 C.5 D.6
3.如图,认真观察作图的过程,点表示的实数是( )
A. B. C. D.
4.如图所示,小宇手里有一张直角三角形纸片,他无意中将直角边折叠了一下,恰好使落在斜边上,且点与点重合,小宇经过测量得知两直角边,,求出的长是( )
A. B. C. D.
5.如图,数轴上的点A表示的数是1,OB⊥OA,垂足为O,且BO=1,以点A为圆心,AB为半径画弧交数轴于点C,则C点表示的数为( )
A. B. C. D.
二、填空题
6.如图,在,,D是中点,,,则 .
7.如图,点M是∠AOB平分线上一点,∠AOB=60°,ME⊥OA于E,OE=,如果P是OB上一动点,则线段MP的取值范围是 .
8.如图, 中, , 为 的中点,若 , ,则 的长为 .
9.如图,已知在中,于点D,,,,动点P从点A出发,向终点B运动,速度为每秒1个单位,运动时间为t秒.当t的值是 秒,是等腰三角形.
10.若等腰三角形腰长为,底边长为,那么它的面积为 .
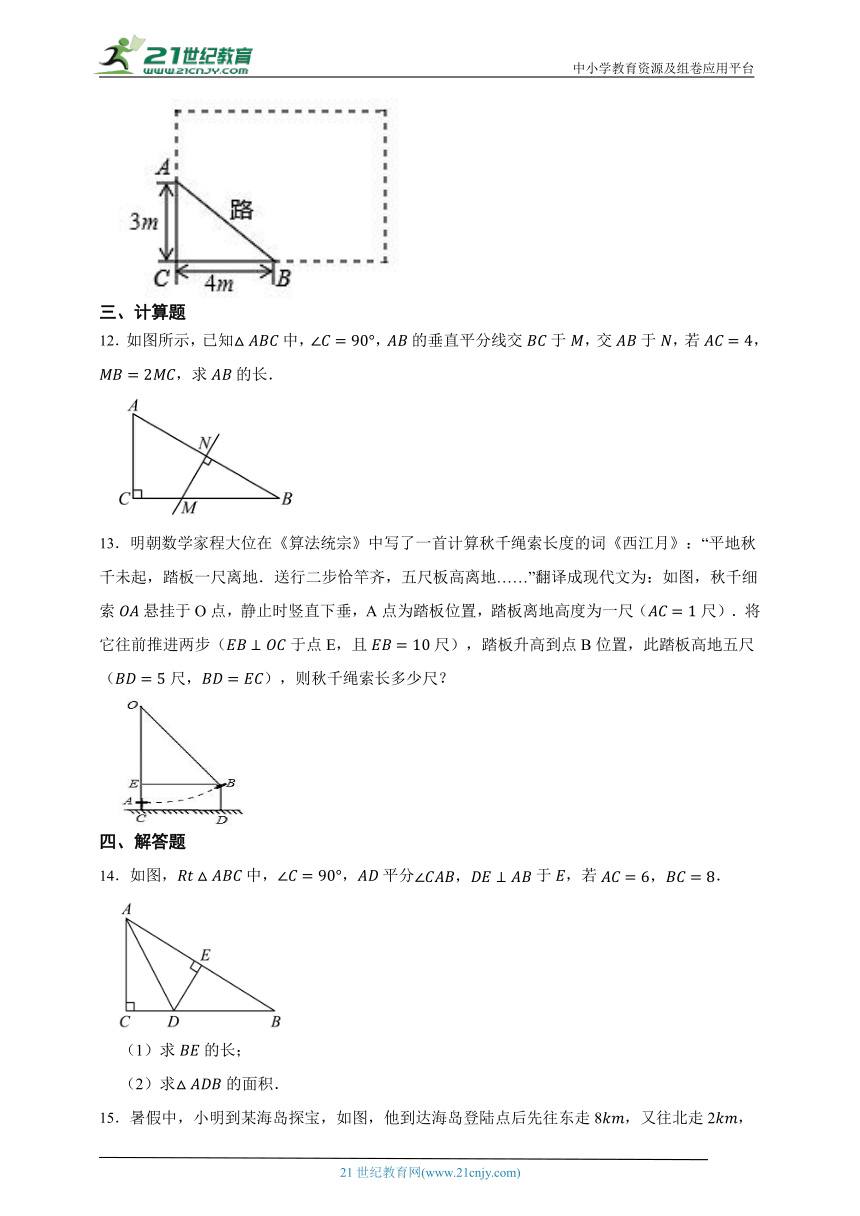
11.如图,校园内有一块长方形草地,为了满足人们的多样化需求,在草地内拐角位置开出了一条路,走此路可以省 m的路.
三、计算题
12.如图所示,已知中,,的垂直平分线交于,交于,若,,求的长.
13.明朝数学家程大位在《算法统宗》中写了一首计算秋千绳索长度的词《西江月》:“平地秋千未起,踏板一尺离地.送行二步恰竿齐,五尺板高离地……”翻译成现代文为:如图,秋千细索悬挂于O点,静止时竖直下垂,A点为踏板位置,踏板离地高度为一尺(尺).将它往前推进两步(于点E,且尺),踏板升高到点B位置,此踏板高地五尺(尺,),则秋千绳索长多少尺?
四、解答题
14.如图,中,,平分于,若.
(1)求的长;
(2)求的面积.
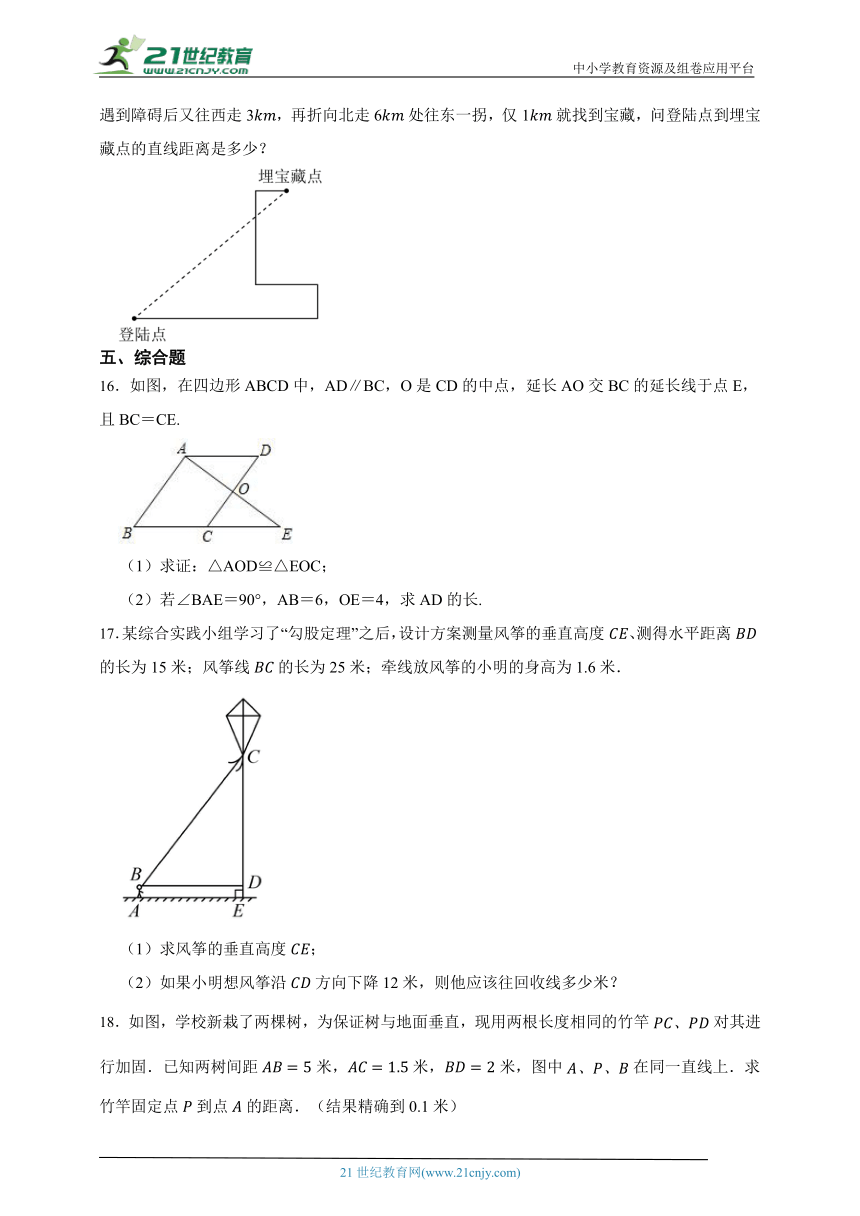
15.暑假中,小明到某海岛探宝,如图,他到达海岛登陆点后先往东走8,又往北走2,遇到障碍后又往西走3,再折向北走6处往东一拐,仅1就找到宝藏,问登陆点到埋宝藏点的直线距离是多少?
五、综合题
16.如图,在四边形ABCD中,AD∥BC,O是CD的中点,延长AO交BC的延长线于点E,且BC=CE.
(1)求证:△AOD≌△EOC;
(2)若∠BAE=90°,AB=6,OE=4,求AD的长.
17.某综合实践小组学习了“勾股定理”之后,设计方案测量风筝的垂直高度、测得水平距离的长为15米;风筝线的长为25米;牵线放风筝的小明的身高为1.6米.
(1)求风筝的垂直高度;
(2)如果小明想风筝沿方向下降12米,则他应该往回收线多少米?
18.如图,学校新栽了两棵树,为保证树与地面垂直,现用两根长度相同的竹竿对其进行加固.已知两树间距米,米,米,图中在同一直线上.求竹竿固定点到点的距离.(结果精确到0.1米)
六、实践探究题
19.问题背景如图,在矩形中,,,动点P、Q分别以、的速度从点A、C同时出发,沿规定路线移动.
问题探究
(1)若点P从点A沿向终点B移动,点Q从点C沿向点D移动,点Q随点P的停止而停止,问经过多长时间P,Q两点之间的距离是?
(2)若点P沿着移动,点P从点A移动到点C停止,点Q从点C沿向点D移动点Q随点P的停止而停止,试探求经过多长时间的面积为?
答案解析部分
1.【答案】A
【知识点】勾股定理
2.【答案】C
【知识点】勾股定理
3.【答案】B
【知识点】实数在数轴上表示;勾股定理
4.【答案】B
【知识点】勾股定理
5.【答案】C
【知识点】实数在数轴上表示;勾股定理
6.【答案】
【知识点】勾股定理;直角三角形斜边上的中线
7.【答案】MP≥1
【知识点】垂线段最短及其应用;角平分线的性质;含30°角的直角三角形;勾股定理
8.【答案】2.5
【知识点】勾股定理;直角三角形斜边上的中线
9.【答案】5或6或
【知识点】勾股定理;等腰三角形的概念
10.【答案】
【知识点】等腰三角形的性质;勾股定理
11.【答案】2
【知识点】勾股定理
12.【答案】8
【知识点】线段垂直平分线的性质;勾股定理
13.【答案】
【知识点】勾股定理
14.【答案】(1)
(2)
【知识点】三角形的角平分线、中线和高;三角形全等及其性质;角平分线的性质;勾股定理
15.【答案】登陆点到宝藏处的距离为10千米
【知识点】勾股定理
16.【答案】(1)证明:如图所示:
∵AD∥BE,
∴∠DAE=∠AEB,
又∵O是CD的中点,
∴CO=DO,
在△AOD和△EOC中,
,
∴△AOD≌△EOC(AAS)
(2)解:∵BC=CE,AO=EO
∴点C、O分别是BE和AE的中点,即CO是△ABE的中位线;
∵OE=4,∴AE=8,
又∵AB=6,
∴在Rt△ABE中,由勾股定理得:
,
CE=BE﹣BC=10﹣5=5.
又∵AD=EC
∴AD=5.
【知识点】全等三角形的判定与性质;勾股定理
17.【答案】(1)米
(2)8米
【知识点】勾股定理
18.【答案】
【知识点】勾股定理
19.【答案】(1)或
(2)4秒或6秒
【知识点】勾股定理;一元一次方程的实际应用-几何问题
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
3.1 勾股定理的探究
一、单选题
1.以直角三角形的三边为边作正方形,三个正方形的面积如图所示,正方形A的面积为( )
A.6 B.36 C.64 D.
2.一个直角三角形的两条直角边分别为和,则第三边长是( )
A.3 B.4 C.5 D.6
3.如图,认真观察作图的过程,点表示的实数是( )
A. B. C. D.
4.如图所示,小宇手里有一张直角三角形纸片,他无意中将直角边折叠了一下,恰好使落在斜边上,且点与点重合,小宇经过测量得知两直角边,,求出的长是( )
A. B. C. D.
5.如图,数轴上的点A表示的数是1,OB⊥OA,垂足为O,且BO=1,以点A为圆心,AB为半径画弧交数轴于点C,则C点表示的数为( )
A. B. C. D.
二、填空题
6.如图,在,,D是中点,,,则 .
7.如图,点M是∠AOB平分线上一点,∠AOB=60°,ME⊥OA于E,OE=,如果P是OB上一动点,则线段MP的取值范围是 .
8.如图, 中, , 为 的中点,若 , ,则 的长为 .
9.如图,已知在中,于点D,,,,动点P从点A出发,向终点B运动,速度为每秒1个单位,运动时间为t秒.当t的值是 秒,是等腰三角形.
10.若等腰三角形腰长为,底边长为,那么它的面积为 .
11.如图,校园内有一块长方形草地,为了满足人们的多样化需求,在草地内拐角位置开出了一条路,走此路可以省 m的路.
三、计算题
12.如图所示,已知中,,的垂直平分线交于,交于,若,,求的长.
13.明朝数学家程大位在《算法统宗》中写了一首计算秋千绳索长度的词《西江月》:“平地秋千未起,踏板一尺离地.送行二步恰竿齐,五尺板高离地……”翻译成现代文为:如图,秋千细索悬挂于O点,静止时竖直下垂,A点为踏板位置,踏板离地高度为一尺(尺).将它往前推进两步(于点E,且尺),踏板升高到点B位置,此踏板高地五尺(尺,),则秋千绳索长多少尺?
四、解答题
14.如图,中,,平分于,若.
(1)求的长;
(2)求的面积.
15.暑假中,小明到某海岛探宝,如图,他到达海岛登陆点后先往东走8,又往北走2,遇到障碍后又往西走3,再折向北走6处往东一拐,仅1就找到宝藏,问登陆点到埋宝藏点的直线距离是多少?
五、综合题
16.如图,在四边形ABCD中,AD∥BC,O是CD的中点,延长AO交BC的延长线于点E,且BC=CE.
(1)求证:△AOD≌△EOC;
(2)若∠BAE=90°,AB=6,OE=4,求AD的长.
17.某综合实践小组学习了“勾股定理”之后,设计方案测量风筝的垂直高度、测得水平距离的长为15米;风筝线的长为25米;牵线放风筝的小明的身高为1.6米.
(1)求风筝的垂直高度;
(2)如果小明想风筝沿方向下降12米,则他应该往回收线多少米?
18.如图,学校新栽了两棵树,为保证树与地面垂直,现用两根长度相同的竹竿对其进行加固.已知两树间距米,米,米,图中在同一直线上.求竹竿固定点到点的距离.(结果精确到0.1米)
六、实践探究题
19.问题背景如图,在矩形中,,,动点P、Q分别以、的速度从点A、C同时出发,沿规定路线移动.
问题探究
(1)若点P从点A沿向终点B移动,点Q从点C沿向点D移动,点Q随点P的停止而停止,问经过多长时间P,Q两点之间的距离是?
(2)若点P沿着移动,点P从点A移动到点C停止,点Q从点C沿向点D移动点Q随点P的停止而停止,试探求经过多长时间的面积为?
答案解析部分
1.【答案】A
【知识点】勾股定理
2.【答案】C
【知识点】勾股定理
3.【答案】B
【知识点】实数在数轴上表示;勾股定理
4.【答案】B
【知识点】勾股定理
5.【答案】C
【知识点】实数在数轴上表示;勾股定理
6.【答案】
【知识点】勾股定理;直角三角形斜边上的中线
7.【答案】MP≥1
【知识点】垂线段最短及其应用;角平分线的性质;含30°角的直角三角形;勾股定理
8.【答案】2.5
【知识点】勾股定理;直角三角形斜边上的中线
9.【答案】5或6或
【知识点】勾股定理;等腰三角形的概念
10.【答案】
【知识点】等腰三角形的性质;勾股定理
11.【答案】2
【知识点】勾股定理
12.【答案】8
【知识点】线段垂直平分线的性质;勾股定理
13.【答案】
【知识点】勾股定理
14.【答案】(1)
(2)
【知识点】三角形的角平分线、中线和高;三角形全等及其性质;角平分线的性质;勾股定理
15.【答案】登陆点到宝藏处的距离为10千米
【知识点】勾股定理
16.【答案】(1)证明:如图所示:
∵AD∥BE,
∴∠DAE=∠AEB,
又∵O是CD的中点,
∴CO=DO,
在△AOD和△EOC中,
,
∴△AOD≌△EOC(AAS)
(2)解:∵BC=CE,AO=EO
∴点C、O分别是BE和AE的中点,即CO是△ABE的中位线;
∵OE=4,∴AE=8,
又∵AB=6,
∴在Rt△ABE中,由勾股定理得:
,
CE=BE﹣BC=10﹣5=5.
又∵AD=EC
∴AD=5.
【知识点】全等三角形的判定与性质;勾股定理
17.【答案】(1)米
(2)8米
【知识点】勾股定理
18.【答案】
【知识点】勾股定理
19.【答案】(1)或
(2)4秒或6秒
【知识点】勾股定理;一元一次方程的实际应用-几何问题
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
