3.3 勾股定理的简单应用 同步练习(含答案)
文档属性
| 名称 | 3.3 勾股定理的简单应用 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 560.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-27 05:50:43 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
3.3 勾股定理的简单应用
一、单选题
1.如图,两个正方形的面积分别是100和36,则字母B所代表的正方形的面积是( )
A.8 B.10 C.64 D.136
2.如图,这是一个长为,宽为,高为的长方体纸箱,是的中点.点处有几滴蜂蜜,一只蚂蚁欲从点出发沿纸箱表面爬行到点处吃蜂蜜,则蚂蚁爬行的最短距离是( )
A. B. C. D.
3.如图,一根竖直生长的竹子,原高一丈(一丈=10尺),折断后,其竹稍恰好抵地(地面水平),抵地处离竹子底端6尺远,则折断处离地面的高度是( )
A.8尺 B.尺 C.尺 D.2尺
4.如图,一根垂直于地面的旗杆在离地面5m处折断,旗杆顶部落在离旗杆底部12m处, 旗杆折断之前的高度是( )
A. B. C. D.
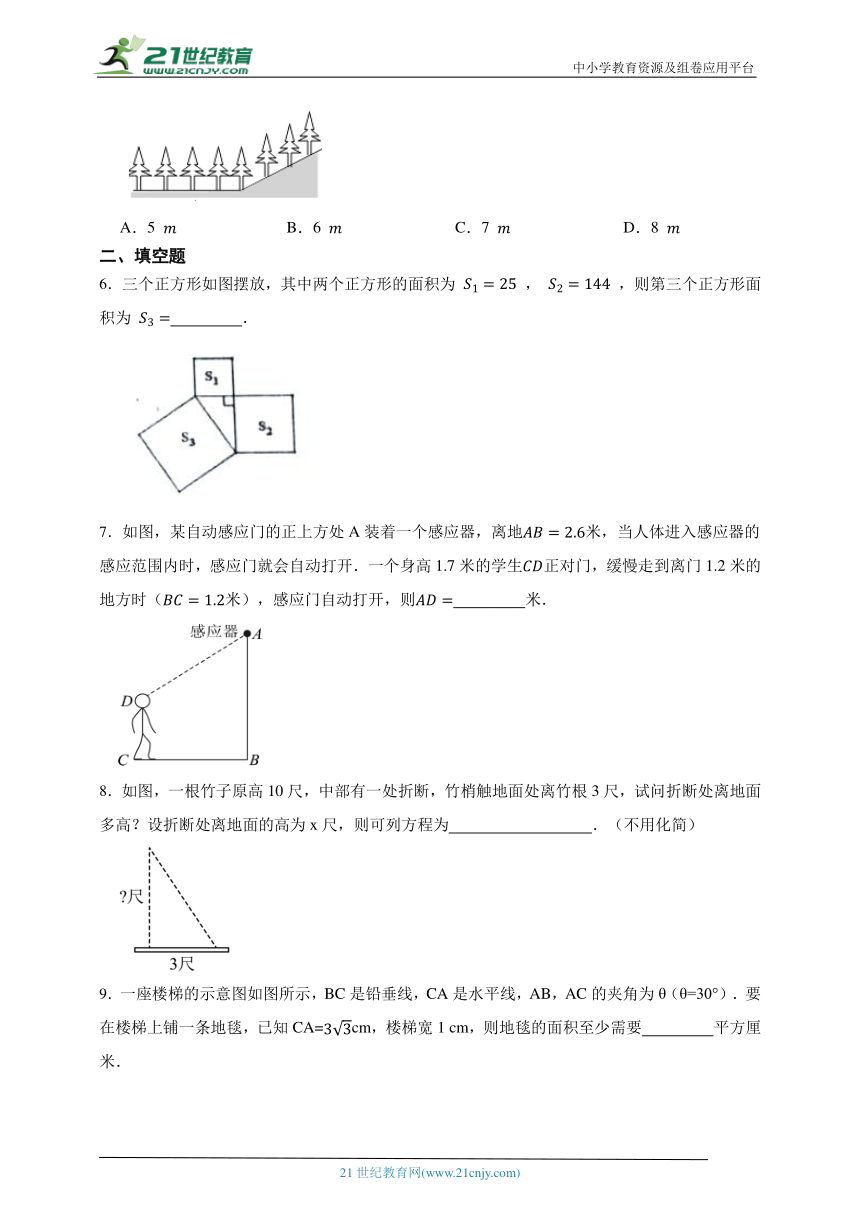
5.如图,在平地上种植树木时,要求株距(相邻两树间的水平距离)为4 .如果在坡度为0.75的山坡上种树,也要求株距为4 ,那么相邻两树间的坡面距离为( )
A.5 B.6 C.7 D.8
二、填空题
6.三个正方形如图摆放,其中两个正方形的面积为 , ,则第三个正方形面积为 .
7.如图,某自动感应门的正上方处A装着一个感应器,离地米,当人体进入感应器的感应范围内时,感应门就会自动打开.一个身高1.7米的学生正对门,缓慢走到离门1.2米的地方时(米),感应门自动打开,则 米.
8.如图,一根竹子原高10尺,中部有一处折断,竹梢触地面处离竹根3尺,试问折断处离地面多高?设折断处离地面的高为x尺,则可列方程为 .(不用化简)
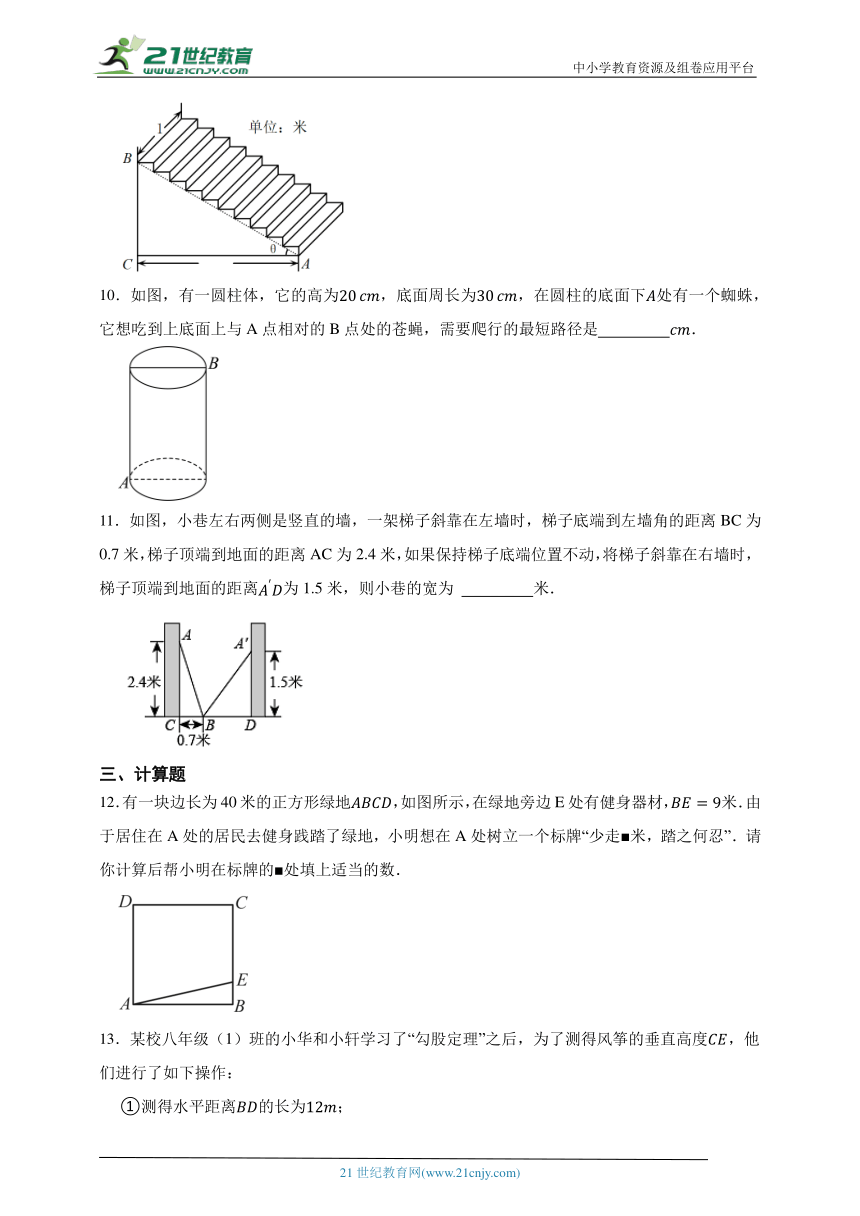
9.一座楼梯的示意图如图所示,BC是铅垂线,CA是水平线,AB,AC的夹角为θ(θ=30°).要在楼梯上铺一条地毯,已知CA=cm,楼梯宽1 cm,则地毯的面积至少需要 平方厘米.
10.如图,有一圆柱体,它的高为,底面周长为,在圆柱的底面下处有一个蜘蛛,它想吃到上底面上与A点相对的B点处的苍蝇,需要爬行的最短路径是 .
11.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离BC为0.7米,梯子顶端到地面的距离AC为2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,梯子顶端到地面的距离为1.5米,则小巷的宽为 米.
三、计算题
12.有一块边长为40米的正方形绿地,如图所示,在绿地旁边E处有健身器材,米.由于居住在A处的居民去健身践踏了绿地,小明想在A处树立一个标牌“少走■米,踏之何忍”.请你计算后帮小明在标牌的■处填上适当的数.
13.某校八年级(1)班的小华和小轩学习了“勾股定理”之后,为了测得风筝的垂直高度,他们进行了如下操作:
①测得水平距离的长为;
②根据手中剩余线的长度计算出风筝线的长为:
③牵线放风筝的小明的身高()为.
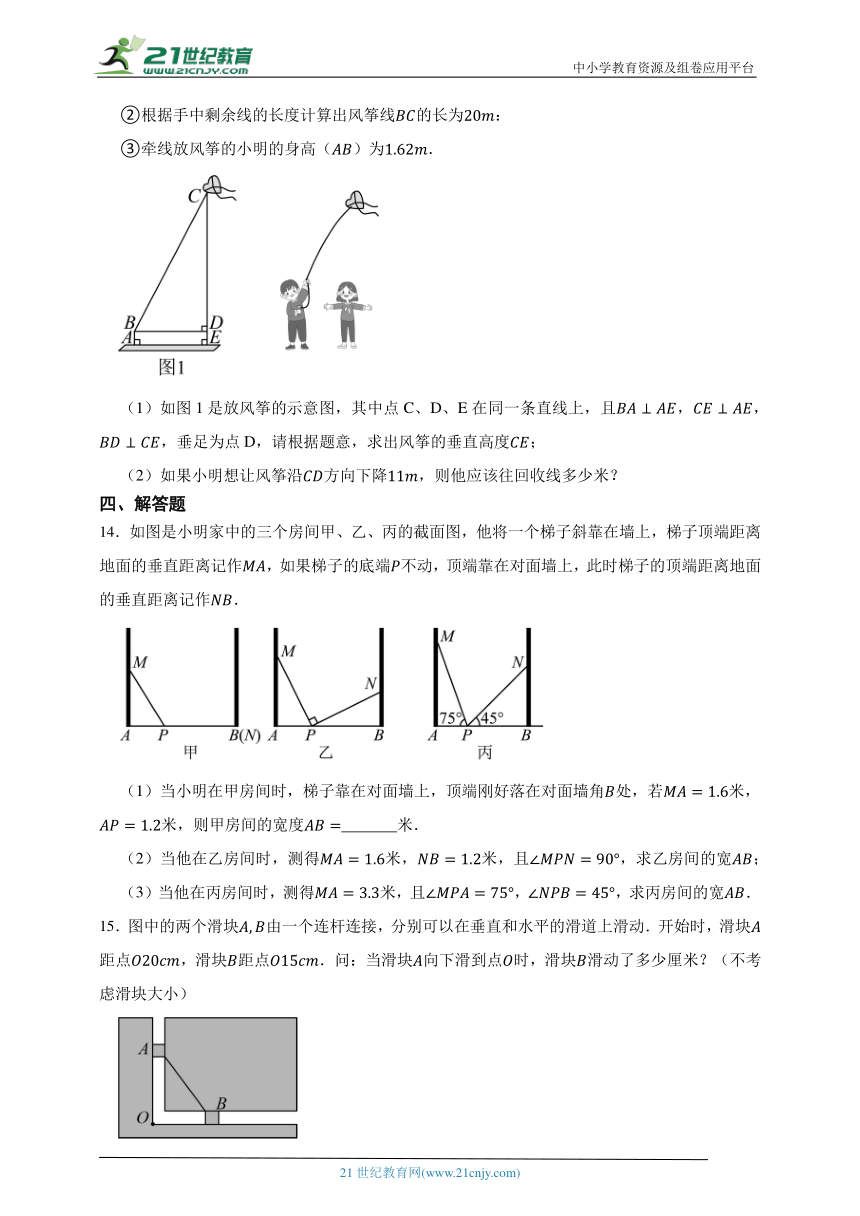
(1)如图1是放风筝的示意图,其中点C、D、E在同一条直线上,且,,,垂足为点D,请根据题意,求出风筝的垂直高度;
(2)如果小明想让风筝沿方向下降,则他应该往回收线多少米?
四、解答题
14.如图是小明家中的三个房间甲、乙、丙的截面图,他将一个梯子斜靠在墙上,梯子顶端距离地面的垂直距离记作,如果梯子的底端不动,顶端靠在对面墙上,此时梯子的顶端距离地面的垂直距离记作.
(1)当小明在甲房间时,梯子靠在对面墙上,顶端刚好落在对面墙角处,若米,米,则甲房间的宽度 米.
(2)当他在乙房间时,测得米,米,且,求乙房间的宽;
(3)当他在丙房间时,测得米,且,,求丙房间的宽.
15.图中的两个滑块由一个连杆连接,分别可以在垂直和水平的滑道上滑动.开始时,滑块距点,滑块距点.问:当滑块向下滑到点时,滑块滑动了多少厘米?(不考虑滑块大小)
五、综合题
16.如图,在一次夏令营活动中,小明从营地点出发,沿北偏东方向走了到达点,然后再沿北偏西方向走了到达目的地点,求两点间的距离.
17.如图,一只蚂蚁从点A沿圆柱表面爬到点B,圆柱高为15cm,底面半径为,蚂蚁爬行的最短路线长为多少?
18.某教学楼走廊左右两侧是竖直的墙和(即).一架梯子在走廊上斜靠在左墙时,梯子底端B到左墙的距离,顶端A到地面的距离.(图中所有点均在同一平面内)
(1)求梯子的长;
(2)如果保持底端位置B不动,将梯子斜靠在右墙上时,若梯子顶端C距离地面的距离,求该教学楼走廊的宽度的长.
六、实践探究题
19.综合与实践
【问题情境】某消防队在一次应急演练中,消防员架起一架长的云梯,如图,云梯斜靠在一面墙上,这时云梯底端距墙脚的距离.
(1)【深入探究】消防员接到命令,按要求将云梯从顶端A下滑到位置上(云梯长度不改变),,那么它的底部B在水平方向滑动到的距离也是吗?若是,请说明理由;若不是,请求出的长度.
(2)【问题解决】在演练中,高的墙头有求救声,消防员需调整云梯去救援被困人员.经验表明,云梯靠墙摆放时,如果云梯底端离墙的距离不小于云梯长度的,则云梯和消防员相对安全.在相对安全的前提下,云梯的顶端能否到达高的墙头去救援被困人员?
答案解析部分
1.【答案】C
【知识点】勾股定理的应用
2.【答案】A
【知识点】勾股定理的实际应用-最短路径问题
3.【答案】C
【知识点】风吹树折模型
4.【答案】D
【知识点】勾股定理的应用
5.【答案】A
【知识点】勾股定理的应用
6.【答案】169
【知识点】勾股定理的应用
7.【答案】1.5
【知识点】勾股定理的应用
8.【答案】
【知识点】风吹树折模型
9.【答案】3+
【知识点】含30°角的直角三角形;勾股定理的应用
10.【答案】25
【知识点】勾股定理的实际应用-最短路径问题
11.【答案】2.7
【知识点】勾股定理的实际应用-梯子滑动问题
12.【答案】8
【知识点】勾股定理的应用
13.【答案】(1)风筝的垂直高度的长为
(2)他应该往回收线
【知识点】勾股定理的实际应用-旗杆高度问题
14.【答案】(1)
(2)米
(3)丙房间的宽是米
【知识点】等边三角形的判定;勾股定理的实际应用-梯子滑动问题
15.【答案】滑块滑动了
【知识点】勾股定理的实际应用-梯子滑动问题
16.【答案】
【知识点】勾股定理的实际应用-(行驶、航行)方向问题
17.【答案】蚂蚁爬行的最短路线长为.
【知识点】勾股定理的实际应用-最短路径问题
18.【答案】(1)
(2)
【知识点】勾股定理的实际应用-梯子滑动问题
19.【答案】(1)解:云梯的底部B在水平方向滑动到的距离不是4πm.
理由如下:
在中,.
.
在中,,
(2)解:若云梯底端离墙的距离刚好为云梯长度的,
则能够到达墙面的最大高度为.
,
因此,云梯的顶端能到达高的墙头去救援被困人员
【知识点】实数的大小比较;勾股定理的应用
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
3.3 勾股定理的简单应用
一、单选题
1.如图,两个正方形的面积分别是100和36,则字母B所代表的正方形的面积是( )
A.8 B.10 C.64 D.136
2.如图,这是一个长为,宽为,高为的长方体纸箱,是的中点.点处有几滴蜂蜜,一只蚂蚁欲从点出发沿纸箱表面爬行到点处吃蜂蜜,则蚂蚁爬行的最短距离是( )
A. B. C. D.
3.如图,一根竖直生长的竹子,原高一丈(一丈=10尺),折断后,其竹稍恰好抵地(地面水平),抵地处离竹子底端6尺远,则折断处离地面的高度是( )
A.8尺 B.尺 C.尺 D.2尺
4.如图,一根垂直于地面的旗杆在离地面5m处折断,旗杆顶部落在离旗杆底部12m处, 旗杆折断之前的高度是( )
A. B. C. D.
5.如图,在平地上种植树木时,要求株距(相邻两树间的水平距离)为4 .如果在坡度为0.75的山坡上种树,也要求株距为4 ,那么相邻两树间的坡面距离为( )
A.5 B.6 C.7 D.8
二、填空题
6.三个正方形如图摆放,其中两个正方形的面积为 , ,则第三个正方形面积为 .
7.如图,某自动感应门的正上方处A装着一个感应器,离地米,当人体进入感应器的感应范围内时,感应门就会自动打开.一个身高1.7米的学生正对门,缓慢走到离门1.2米的地方时(米),感应门自动打开,则 米.
8.如图,一根竹子原高10尺,中部有一处折断,竹梢触地面处离竹根3尺,试问折断处离地面多高?设折断处离地面的高为x尺,则可列方程为 .(不用化简)
9.一座楼梯的示意图如图所示,BC是铅垂线,CA是水平线,AB,AC的夹角为θ(θ=30°).要在楼梯上铺一条地毯,已知CA=cm,楼梯宽1 cm,则地毯的面积至少需要 平方厘米.
10.如图,有一圆柱体,它的高为,底面周长为,在圆柱的底面下处有一个蜘蛛,它想吃到上底面上与A点相对的B点处的苍蝇,需要爬行的最短路径是 .
11.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离BC为0.7米,梯子顶端到地面的距离AC为2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,梯子顶端到地面的距离为1.5米,则小巷的宽为 米.
三、计算题
12.有一块边长为40米的正方形绿地,如图所示,在绿地旁边E处有健身器材,米.由于居住在A处的居民去健身践踏了绿地,小明想在A处树立一个标牌“少走■米,踏之何忍”.请你计算后帮小明在标牌的■处填上适当的数.
13.某校八年级(1)班的小华和小轩学习了“勾股定理”之后,为了测得风筝的垂直高度,他们进行了如下操作:
①测得水平距离的长为;
②根据手中剩余线的长度计算出风筝线的长为:
③牵线放风筝的小明的身高()为.
(1)如图1是放风筝的示意图,其中点C、D、E在同一条直线上,且,,,垂足为点D,请根据题意,求出风筝的垂直高度;
(2)如果小明想让风筝沿方向下降,则他应该往回收线多少米?
四、解答题
14.如图是小明家中的三个房间甲、乙、丙的截面图,他将一个梯子斜靠在墙上,梯子顶端距离地面的垂直距离记作,如果梯子的底端不动,顶端靠在对面墙上,此时梯子的顶端距离地面的垂直距离记作.
(1)当小明在甲房间时,梯子靠在对面墙上,顶端刚好落在对面墙角处,若米,米,则甲房间的宽度 米.
(2)当他在乙房间时,测得米,米,且,求乙房间的宽;
(3)当他在丙房间时,测得米,且,,求丙房间的宽.
15.图中的两个滑块由一个连杆连接,分别可以在垂直和水平的滑道上滑动.开始时,滑块距点,滑块距点.问:当滑块向下滑到点时,滑块滑动了多少厘米?(不考虑滑块大小)
五、综合题
16.如图,在一次夏令营活动中,小明从营地点出发,沿北偏东方向走了到达点,然后再沿北偏西方向走了到达目的地点,求两点间的距离.
17.如图,一只蚂蚁从点A沿圆柱表面爬到点B,圆柱高为15cm,底面半径为,蚂蚁爬行的最短路线长为多少?
18.某教学楼走廊左右两侧是竖直的墙和(即).一架梯子在走廊上斜靠在左墙时,梯子底端B到左墙的距离,顶端A到地面的距离.(图中所有点均在同一平面内)
(1)求梯子的长;
(2)如果保持底端位置B不动,将梯子斜靠在右墙上时,若梯子顶端C距离地面的距离,求该教学楼走廊的宽度的长.
六、实践探究题
19.综合与实践
【问题情境】某消防队在一次应急演练中,消防员架起一架长的云梯,如图,云梯斜靠在一面墙上,这时云梯底端距墙脚的距离.
(1)【深入探究】消防员接到命令,按要求将云梯从顶端A下滑到位置上(云梯长度不改变),,那么它的底部B在水平方向滑动到的距离也是吗?若是,请说明理由;若不是,请求出的长度.
(2)【问题解决】在演练中,高的墙头有求救声,消防员需调整云梯去救援被困人员.经验表明,云梯靠墙摆放时,如果云梯底端离墙的距离不小于云梯长度的,则云梯和消防员相对安全.在相对安全的前提下,云梯的顶端能否到达高的墙头去救援被困人员?
答案解析部分
1.【答案】C
【知识点】勾股定理的应用
2.【答案】A
【知识点】勾股定理的实际应用-最短路径问题
3.【答案】C
【知识点】风吹树折模型
4.【答案】D
【知识点】勾股定理的应用
5.【答案】A
【知识点】勾股定理的应用
6.【答案】169
【知识点】勾股定理的应用
7.【答案】1.5
【知识点】勾股定理的应用
8.【答案】
【知识点】风吹树折模型
9.【答案】3+
【知识点】含30°角的直角三角形;勾股定理的应用
10.【答案】25
【知识点】勾股定理的实际应用-最短路径问题
11.【答案】2.7
【知识点】勾股定理的实际应用-梯子滑动问题
12.【答案】8
【知识点】勾股定理的应用
13.【答案】(1)风筝的垂直高度的长为
(2)他应该往回收线
【知识点】勾股定理的实际应用-旗杆高度问题
14.【答案】(1)
(2)米
(3)丙房间的宽是米
【知识点】等边三角形的判定;勾股定理的实际应用-梯子滑动问题
15.【答案】滑块滑动了
【知识点】勾股定理的实际应用-梯子滑动问题
16.【答案】
【知识点】勾股定理的实际应用-(行驶、航行)方向问题
17.【答案】蚂蚁爬行的最短路线长为.
【知识点】勾股定理的实际应用-最短路径问题
18.【答案】(1)
(2)
【知识点】勾股定理的实际应用-梯子滑动问题
19.【答案】(1)解:云梯的底部B在水平方向滑动到的距离不是4πm.
理由如下:
在中,.
.
在中,,
(2)解:若云梯底端离墙的距离刚好为云梯长度的,
则能够到达墙面的最大高度为.
,
因此,云梯的顶端能到达高的墙头去救援被困人员
【知识点】实数的大小比较;勾股定理的应用
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
